如何培养学生“说”数学的能力

摘 要:数学教育的本质是思维训练,语言是学生思维的外显形态。小学数学教师应注重学生的“说”,着力引导学生用口头语言表达自己的思维过程,由此了解学生的具体情况,有针对性地进行引导,使学生扎实掌握学习内容,提升思维水平,发展“说”数学的能力。一般情况下,教师要围绕教学目标、教学内容和教学反馈,采用适当的策略培养学生“说”数学的能力。文章对此进行了分析,以期为相关教师提供参考。
关键词:小学数学;“说”数学;能力培养策略
中图分类号:G427 文献标识码:A 文章编号:2097-1737(2023)32-0041-03
维果斯基在其著作《思维与语言》中指出了思维与语言之间的依存关系。在他看来,思维和语言是一个相互促进的发展过程。在这个过程中,个体的思维能力和语言能力都将得到提高。众所周知,数学教育的本质是思维训练[1],而语言表达是学生思维过程、结果的外显形态。教师通过引导学生“说”数学,既可以了解他们的思维情况,又可以了解他们的数学知识掌握情况。由此,教师可以有针对性地进行教学指导,使学生积极思维、深入探究,顺其自然地掌握知识,提高思维水平,增强“说”数学的能力。所谓“说”数学是指在数学学习过程中,学生在教师的引导下用“说”的形式表达数学学习思路、学习方法、学习结果、学习困惑、学习反思等,其他学生认真倾听、质疑、交流、总结,由此强化数学认知,发展思维能力、“说”数学能力的一种学习方式。在本文中,笔者将详细论述培养学生“说”数学能力的策略。
一、明确目标,提高“说”的适切性
“说”数学是落实教学目标的“服务者”。教学目标是“说”数学的导向[2]。简单地说,围绕明确的教学目标引导学生“说”数学,可以增强学生“说”的适切性,便于学生“说”有所得。因此,小学数学教师应先设定教学目标,再引导学生“说”数学。“依标而教”是新课程改革的基本理念。教师应研读课程标准,结合具体的教学内容,设定明确的教学目标。
例如,“小数的初步认识”是苏教版小学数学教材三年级(下册)第八单元内容。该内容贴近学生生活实际,方便学生迁移已有认知进行表达。基于此,教师可明确“说”数学目标:(1)体验真实情境,从具体事件中感受小数的意义;(2)在特定的情况下进行表达,感知小数的意义;(3)学会结合自身已有经历、认知,反复表达,感悟小数的意义,增强“说”数学的能力。在此教学目标的指引下,教师能够把握教学内容和学生生活的联系,创设生活情境,引导学生在体验情境的过程中“说”数学,促使学生获得良好发展。
二、紧扣内容,提高“说”的合理性
(一)“说”概念
数学概念是基本的数学教学内容,具有逻辑性、抽象性。教师应以数学概念的形成过程为切入点,组织“说”数学活动,使学生在探索、交流、归纳、总结的过程中深刻认知数学概念。
例如,在教学“射线”概念时,教师在黑板上画出一条线段,并延长线段的一端。学生认真观看,思考问题:“这还是线段吗?”在思考时,大部分学生调动已有认知,给出否定的回答。教师引导学生说明这是一条什么样的“线”。大部分学生回想自学过程,提到了射线。于是,教师鼓励他们研究射线的端点和长度。学生迁移自学认知,在纸张上画出不同的射线,认真观察,了解射线的端点和长度,并主动与小组成员交流,“说”射线的特点,由此碰撞出思维火花,进一步认识射线。
在学生自主、合作探究后,教师随机选择代表,鼓励学生描述射线的特点。有的学生描述道:“射线就像是从手电筒射出的一束光,有一个端点,长度不限。”有的学生描述道:“射线只有一个端点,另外一端可以无限延长。”还有学生描述道:“将线段的一个端点去掉,
可以得到一条射线。这条射线可以无限延长。”教师认真倾听,并在学生“说”完后耐心地总结射线的特点,
帮助学生强化认知。之后,教师采用同样的方式引导学生探究直线。在学生了解了直线、射线、线段后,教师继续组织“说”数学活动,鼓励他们建立表格,对比直线、线段、射线的图形、端点和能否测量,明确它们之间的差异,并进行口头表述。
在经历概念形成的过程中,学生体验了多样的“说”数学活动,一步步地了解了直线、射线、线段的概念及其之间的相同点和不同点,建立了深刻的认知,同时自然而然地发展了“说”数学的能力和思维能力,可谓一举多得。
(二)“说”性质
数学性质是数学教材中的重要内容。部分小学生过度依赖教材,直接识记性质内容。学生要敢于质疑数学教材,表达个人看法,如此方能做到知其然且知其所以然。所以,数学教师应以教材中的性质内容为立足点,引导学生质疑、表达。
例如,在“小数的基本性质”这节课上,教师利用电子白板展示商店货架上的价签,创设生活情境。学生在体验情境的过程中得到一些信息:0.1元、0.10元、0.100元。基于此,教师引导他们思考:“这三个数是否相等?如何验证?”学生因此产生探究欲望,发散思维,设想不同的验证方法,灵活应用。
在学生自主验证后,教师鼓励他们“说”。有的学生操作电子白板,认真讲道:“将课件中的米尺平均分為10份,每一份是1分米。1分米可以用0.1米来表示。之后,将1分米平均分为10份,每份是1厘米。此时扩大米尺,将其平均分为100份,取其中的10份,用小数表示为0.10 m。继续平均分,将1厘米平均分为10份,每份是1毫米,100份是100毫米,即0.100 m。
因此,1分米=10厘米=100毫米,1分米=0.1米,
10厘米=0.10米,100毫米=0.100米。所以,0.1米=
0.10米=0.100米。”
其他学生一边观看一边倾听,获取清晰的思路,汲取对比经验。之后,其他学生毛遂自荐,操作电子白板,表述其他思路。教师则依据全体学生代表“说”的情况,概述不同的验证方法及结论。同时,教师引导学生思考:“根据不同的验证方法,可以得出什么样的结论?”学生纷纷回想不同的验证方法,认真对比,发现共同之处,细心总结。有的学生说道:“从左向右看,
当小数的末尾加上0时,小数的大小不变;从右向左看,当小数的末尾去掉0时,小数的大小不变。”基于此,教师追问:“教材是如何描述这一结论的?这一结论中的哪个词最关键?”学生迁移已有认知走进数学教材中,反复诵读相关的性质内容,找寻出关键信息——小数的末尾。学生主动表述自己的理解:“在小数的末尾加0或去0,小数的大小不变。”
如此一来,学生不但通过思考、观察、总结,一步步地得出了小数的基本性质,建构了深刻的认知,还切实地锻炼了“说”数学的能力,有利于提高数学学习水平。
(三)“说”算理、算法
数学运算是数学学科的基础内容。算理、算法是学生必须掌握的运算内容,也是学生提高数学运算水平的支撑。在传统的数学教学中,部分教师忽视算理、算法,直接告诉学生结论。学生在未全面参与课堂教学的情况下,无法深刻地掌握算理、算法,不利于发展数学运算能力。“说”算理、算法是学生全面参与课堂教学的具体途径。在“说”算理、算法的过程中,学生会使用恰当的方法进行探究,得出结论,并将之转化为自己的语言,由此扎实掌握算理、算法,获取相关方法,提高数学学习效率。对此,教师应引导学生“说”算理、算法。
例如,在教学“两位数乘两位数的笔算乘法”时,教师在电子白板上展示情境图,引导学生读图,获取信息,列出算式。大部分学生在已有认知的助力下,列出乘法算式“14×12”,教师鼓励他们设想计算方法。学生开动脑筋,联想已有的学习经历,确定使用点子图进行計算。同时,学生在纸张上画出点子图,展现自己的计算思路。
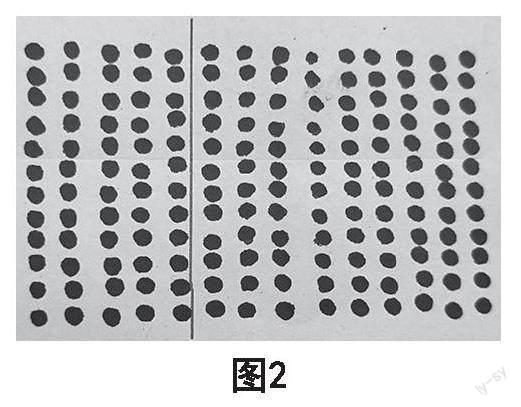
在得出计算结果后,学生毛遂自荐,在黑板上画出不同的点子图,并描述计算过程。如一位学生代表画出
点子图(如图1),并描述道:“10×14=140,2×14=28,
140+28=168。”
另一位学生代表也画出点子图(如图2),并描述道:“9×12=108,5×12=60,108+60=168。”
教师赞赏学生的良好表现,并在黑板上画出其他点子图,介绍其他计算方法。然后,教师引导学生观察黑板上的所有点子图,引导学生对比、总结它们的共同点。全体学生细心观察,得出结论——先将所有点分成两份,计算出每一份的数量,再相加。此时,教师引导学生思考:“这样做的目的是什么?”很多学生容易联想到“让相乘的数字变小,降低计算难度”。教师就此点拨,引导学生建立两位数乘两位数与两位数乘一位数、两位数乘整十数之间的关系。
经过不断探究、“说”数学,大部分学生获取了两位数乘两位数的方法。教师鼓励他们描述计算时的注意事项。在整个教学过程中,教师没有直接告诉学生结论,而是指导学生自主探究。在进行探究时,学生质疑、思考,得出结论,认真表达,不断完善思路和结论,了解两位数乘两位数的算理和算法,积累“说”
数学的经验。
三、重视反馈,增强“说”的积极性
(一)口头语言评价学生的“说”
口头语言评价是教师在与学生交流的过程中,根据学生“说”的内容而做出的口头启示、引导,能使学生及时了解自身学情,提高学习兴趣。
例如,在学生探究“射线”后,教师向他们发问:
“什么是射线?怎样画出射线?”学生联想课堂学习内容,描述画射线的方法。有学生描述道:“先画出一个端点,再从端点出发,画出一条可以无限延长的线。”有学生描述道:“将一条直线一分为二,在两条直线上的一端各自画上一个点,可以得到射线。”很显然,学生表述的射线画法是不规范的。对此,教师进行口头评价:“大家的想法很有创意,但是有可行性吗?请大家试着按照这些方法画一画,看看能否得到射线?”学生产生了好奇心,认真思索每种方法,细心绘画,仔细判断。之后,学生主动展现各自的作品,并表述自己的判断。
由此可见,在口头评价的激励下,学生进行深入探究,可以进一步认知学习内容,发散思维,锻炼“说”
数学的能力。
(二)非口头语言评价学生的“说”
非口头语言评价包括辅助语言评价和类语言评价。辅助语言评价包括语速、音调、音量等。类语言评价包括笑、叹息、咳嗽、微笑、皱眉、瞪眼等。与口头语言评价一样,非口头语言评价可以影响学生“说”数学的积极性。教师应始终关注学生“说”数学的表现,
及时进行非口头语言评价[3]。
例如,在“比较角的大小”这节课上,教师鼓励学生与同桌合作制作角,介绍角的顶点、边、角度。在学生制作时,教师巡视课堂,发现一组学生手忙脚乱地操作两根绳子,试着用这两根绳子“拼出”一个角。教师确定他们的做法是正确的,但太着急。于是,教师走到他们的身边,用手拍拍他们的肩膀,并动手帮他们拉紧绳子。他们在教师的激励下平复情绪,积累经验,主动改进不正确的行为。
在学生完成制作任务后,教师选择该组学生展示成果,描述角的边、顶点和角度。当学生出现表述不流畅的问题时,教师要用口型提示,促使学生解决问题。如此。学生不仅可以做到学用结合,切实理解学习内容,还可以获得心灵满足,提升“说”数学的兴趣。
四.结束语
综上所述,有效的“说”数学活动可以使学生获得数学学习主动权。学生通过“说”数学,既可以从“要我学”变为“我要学”,又可以扎实掌握学习内容,锻炼思维能力,提高“说”数学能力。因此,小学数学教师应尊重学生的学习主体地位,联系课程标准要求、学生学情和教学内容,设计“说”数学教学目标;接着,
以具体的数学教学内容为依据,如数学概念、数学性质、算理算法,引导学生体验多样的“说”数学活动。在教学过程中,教师要善于融入口头语言评价和非口头语言评价,推动学生兴致高昂地“说”数学,让学生在掌握所学的同时发展“说”数学能力。
参考文献
[1] 曾一英.小学数学课堂“说数学”能力培养的有效策略[J].当代家庭教育,2022(30):125-128.
[2] 高梦妮.小学低段学生“说数学”能力培养策略研究[D].重庆:西南大学,2022.
[3] 李旭.浅谈“说数学、促思维”在小学高段教学中的实践与研究[J].新课程,2022(18):69.
作者简介:张勤峰(1977.1-),女,江苏沭阳人,
任教于江苏省南京市丁家庄小学,一级教师,本科学历。

