如何利用图形的平移解决规律探索题
郭祖涛

摘要:在初中数学日常思维训练中,经常会遇到规律探索题.这类题虽然趣味性强,但学生的实际解决水平比较弱,导致大部分学生在见到此类问题时往往避之不及.针对该问题,教师一方面要认识到规律探索题是中考命题热点题型,另一方面积极探索解决此类问题的方法,帮助学生不断提高探究能力.本文中结合实例探究如何利用图形的平移解决规律探索类问题.
关键词:图形的平移;规律探索题;趣味;方法
根据教学经验,规律探索题在日常检测与中考中出现的几率非常大,且难度较大,往往是学生提高学业水平的“拦路虎”[1].基于此,本文中从例题分析出发,尝试总结出利用图形的平移解决规律探索题的方法.
1 规律探索题的素养体现
规律探索题之所以是初中数学教学的难点,是因为规律的探索尤为注重对规律性特征的把握,而这又依赖于从情境式的问题中寻找隐含的数学关系,整个过程可以看成是对规律性结构的重建与加工.因此,规律探索题主要体现了以下素养:
首先,数学抽象与逻辑推理素养.将图形的平移抽象成点的变化,通过点的变化进行逻辑推理,并得到其他点的坐标,这体现了数学抽象与逻辑推理素养.
其次,直观想象与逻辑推理素养.通过图形可直观地观察点的运动情况,并总结出点的变化规律,从而运用逻辑推理得到其他点的坐标,这是直观想象与逻辑推理素养的体现.
最后,逻辑推理及数学运算素养.点的运动会导致坐标的变化,而其变化规律既要通过逻辑推理得到,同时应用其规律推理其他点的坐标时,又是数学运算的体现.所以,应用图形的平移解决规律探索题时,体现了逻辑推理及数学运算素养.
2 例题分析及解法评析
下面结合例题分析尝试总结利用图形的平移解决规律探索题的方法.
例1 已知A1,A2,A3,A4,A5,……的坐标分别为(1,0),(1,1),(-1,1),(-1,-1),(2,-1),……,如图1进行下去,则点A2 013的坐标是( ).
A.(504,-503)
B.(504,504)
C.(-504,504)
D.(-504,-504)
解析:根据观察不难发现,凡是角标数字为4的倍数的点全部位于第三象限.
因为2 013÷4=503……1,所以
A2 013在第四象限,故
A2 012在第三象限.
由2 012÷4=503,可知
A2 012是第三象限第503个点.
所以A2012的坐标应是(-503,-503).故
A2013的坐标应是 (504,-503).
故选答案:A.
解法评析:本题主要考查学生观察规律、总结规律和应用规律解决问题的能力.规律的观察重在用数学眼光看待问题,规律的总结重在用数学的语言表达问题,规律的应用重在用数学方法解决问题,这是学科素养的体现.在解决这类问题时,抓住角标的变化规律,就可以抓住点的变化规律[2].
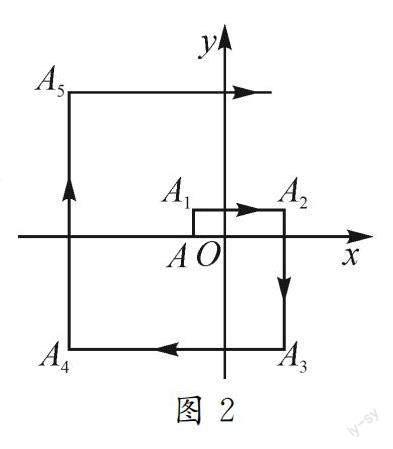
例2 如图2所示,在平面直角坐标系中,将点A(-1,0)做如下的连续平移,A(-1,0)→A1(-1,1)→A2(2,1)→A3(2,-4)→A4(-5,-4)→A5(-5,5)……,按此规律平移下去,则点A102的坐标是( ).
A.(100,101)
B.(101,100)
C.(102,101)
D.(103,102)
分析:根据题意可知,点A平移时所在象限每4次为一个周期.由102÷4=25……2,可知点A102的坐标与点A4n+2的坐标规律相同,分别求出A2,A6,A10的坐标,找出规律后即可求解.
解析:根据将点A(-1,0)作如下的连续平移,A(-1,0)→A1(-1,1)→A2(2,1)→A3(2,-4)→A4(-5,-4)→A5(-5,5)……,得到其中的规律就是点A平移时所在象限每4次为一个周期.
因为102÷4=25……2,所以
点A102的坐标与点A4n+2的坐标规律相同.
因为A2,A6,A10的坐标分别是(2,1),(6,5),(10,9),以此类推,
点A4n+2的坐标是(4n+2,4n+1),所以
A102的坐标是(102,101).
故选答案:C.
解法评析:本题与例1的解法类似,都是找出点的下标的规律,据此找出点A的平移规律或平移周期,最后根据这一规律计算即可.
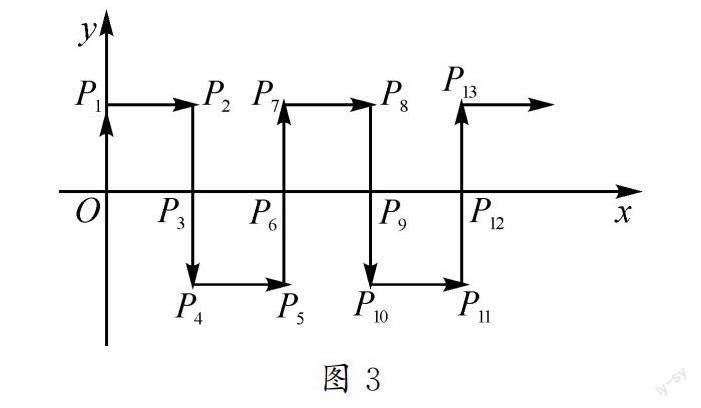
例3 有一个从原点出发的动点,按照如图3所示的箭头移动,每次移动一个单位长度,依次得到点P1,P2,P3,P4,P5,P6,……,它们的坐标分别是(0,1),(1,1),(1,0),(1,-1),(2,-1),(2,0),……,按照这样的规律进行下去,点P60的坐标是.
分析:根据图形分别求出n=3,6,9时对应的点的坐标,可知点P3n(n,0),将n=20代入可得.
解:因为P3(1,0),P6(2,0),P9(3,0),……,所以
P3n(n,0).
当n=20时,P60(20,0).
故填答案:(20,0).
解法评析:本题考查了點的坐标的变化规律,仔细观察图形,分别求出n=3,6,9时对应的点的坐标是解题的关键.
3 方法总结
通过上面几道例题的分析和解法评析不难发现,利用图形的平移解决规律探索题,既有趣又探究意义十足,是训练学生数学思维的重要方法.下面对利用图形的平移解决规律探索题的方法作如下总结:
首先,利用图形的平移解决规律探索题一定会应用图形的平移知识,其中主要涉及点的平移规律[3].所以,在教学中需帮助学生不断巩固和强化图形平移中点的平移规律.笔者建议,教师可通过例题变式或举一反三的形式,让学生接触各种点的运动方式,如例1、例2的“旋转式”或例3的“S式”等.这样一来,学生就会不断积累相应的分析与解题经验,更有利于问题的解决.
其次,奠定知识基础后,接着通过图形观察点的运动状态.通常点的运动蕴藏着一定规律,这个规律不仅呈现出周期变化,而且往往与点的角标规律有关.所以,结合序号分析点的角标的变化规律对解决这类问题非常关键.但是,有时候角标的规律可能比较难分析,这就需要教师补充规律探索中的数字式规律,从而帮助学生弥补这一不足.
最后,在找到点的角标规律后,将题中要求的点的角标与该规律联系起来,并进行相关的计算即可求解.这种计算往往比较简单,但仍需学生多加注意.
综上所述,尽管规律探究题的难度不小,且其中点的运动过程需用心分析,但并非意味着学生遇到此类问题时可“绕道而行”,相反应“迎难而上”.因此,作为一线初中数学教师要善于从题中总结出解题方法,帮助学生解决疑难问题[4].只有这样,学生的探究能力和问题解决能力才会得到提高.
参考文献:
[1]明廷军. 关注图形平移过程 掌握图形变化规律——微课教学的实践探索[J]. 中学数学研究(华南师范大学版), 2020(18):48-50.
[2]贺洪秋. 精心设计学习问题 促进目标有效达成——以《图形的平移》教学为例[J]. 数学大世界(中旬), 2021(8):55-56.
[3]安德枝. 借助图形运动 培养转化意识 ——以《运用平移解决问题》教学为例[J]. 湖北教育(教育教学), 2020(8):73-74.
[4]林海. 利用平移变换的思想解决几何综合题的策略与方法[J]. 求知导刊, 2020(43):65-66.
作者单位:安徽省宿州市砀山县晨光中学

