3Z-Ⅰ型行星轮系传动效率研究

张 军，乔红娇，熊杨寿

齿轮传动作为目前最为广泛的传动形式之一，其传动效率一直是国内外学者的研究重点.MARTIN［1］和王成［2］在齿轮啮合过程中将摩擦因数作为定值，提出了提高齿轮转动效率的设计方法.杨剑飞等［3］结合弹流摩擦系数模型及直齿轮的啮合特性、啮合过程中齿面载荷、齿面摩擦力的时变性、单双齿啮合特性，对直齿轮效率进行了研究.ANDERSON等［4］针对齿轮的几何尺寸、扭矩、转速及润滑油黏度的不同，进行齿轮啮合时能量损失的研究，得出高精度和大直径齿轮具有较高传动效率的结论.刘万山等［5］通过计算啮合角变化下的滑动摩擦和滚动摩擦功率损耗，获得非圆齿轮传动的啮合效率.陈立锋等［6］和董皓等［7］在考虑齿轮啮合过程中摩擦因素变化的前提下，对直齿轮啮合过程中摩擦功耗的计算和直齿面齿轮滑动摩擦啮合效率的问题进行了研究.

微线段齿轮［8］是一种新型齿轮，相较于传统的渐开线齿轮，其具有更高的承载能力、耐磨性和效率［9-13］.目前，针对微线段齿轮传动效率的研究已得到实验验证［14］，且建立了微线段齿轮传动效率的计算公式［12］，但在传动效率的计算过程中，将摩擦因数作为定值处理，得出的结论与实际结果偏差较大.本文针对微线段齿轮，对啮合过程中摩擦因数的变化进行研究，建立微线段齿轮传动效率的计算模型，并与相同参数的渐开线齿轮传动效率的计算结果进行对比，最后进行实验验证，为微线段齿轮的相关研究提供依据.

1 渐开线齿轮传动效率计算

1.1 渐开线齿轮的摩擦功

图1 为一对标准渐开线直齿轮啮合示意图.齿轮1 为主动轮，齿轮2 为从动轮，角速度分别为ω1、ω2，基圆半径分别为rb1、rb2. 直线N1N2为该对齿轮的理论啮合线，K为实际啮合线上一点.

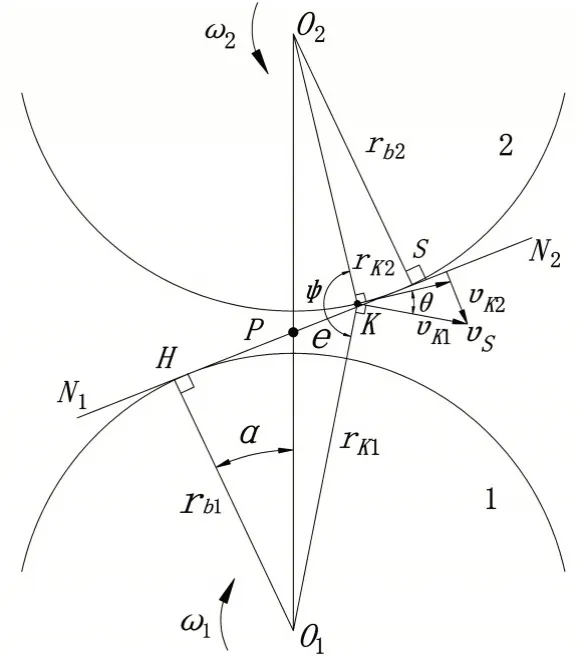
图1 渐开线齿轮啮合示意图

vs为点K相对于节点P的滑动速度，e为啮合点K到节点P的距离-----PK，则

在时间dt内所做的摩擦功dA'为：

式中：Fn为齿面的法向载荷，μ为摩擦因数.

在时间dt内啮合点在啮合线上的移动距离de为：

联立式（2）（3）得：

1.2 渐开线齿轮的摩擦因数计算

根据CIOC［15］的非牛顿热弹性润滑理论，XU 等［16-17］推导出弹流润滑状态下齿轮啮合齿面滑动摩擦因数的计算公式，并进行了相关实验验证，其结论包括：现有的滑动摩擦因数计算公式求得的结果一般较大；齿轮在节线附近啮合时，滑动摩擦因数趋近于0；齿面啮合点的滑滚比绝对值越小，滑动摩擦因数越小.

XU 所得的摩擦因数计算公式为：

式中：Ph为赫兹应力；SR为滑滚比，SR=vs/ve，vs、ve分别为齿面啮合点处的相对滑动速度和卷汲速度；v0为润滑油的动力粘度；R为齿面啮合点处的综合曲率半径；s为齿面粗糙度；系数b1=-8.916 4，b2= 1.033 0，b3= 1.036 0，b4=-0.354 0，b5= 2.812 0，b6=-0.100 6，b7=0.752 7，b8=-0.390 9，b9= 0.620 3.

赫兹应力、滑滚比、齿面相对滑动速度、卷汲速度及综合曲率半径等参数在齿轮啮合过程中均随啮合点在啮合线上的位置变化而变化，故均可将这些参数表达为与啮合点位置相关的函数关系式.

1.2.1 综合曲率半径计算

如图1 所示，啮合点位于点K时，齿面的曲率半径分别为：

式中：ri为齿轮i（i= 1，2）的节圆半径；α为齿轮压力角大小.

则点K处的综合曲率半径为：

1.2.2 赫兹应力计算

根据赫兹理论，啮合点处的赫兹应力为：

式中：ωl为单位齿宽载荷，综合弹性模量E'为：

式中：E1、E2分别为齿轮1、2 的弹性模量；μ1、μ2分别为齿轮1、2 的泊松比.

现对啮合线上不同位置的单位齿宽载荷进行分析.

如图2 所示，以节点P为原点，沿啮合线方向为正方向建立x轴坐标系.其中，H为啮入点，S为啮出点，HI和QS为实际啮合线上的双啮合区，IQ为单啮合区为基圆齿距.

图2 渐开线齿轮啮合线坐标系

根据齿轮啮合原理，啮合线上五点在该坐标系上的坐标分别为：

式中：rai、rbi分别为齿轮（i= 1，2）的齿顶圆半径和齿根圆半径.

在齿轮啮合过程中，单位齿宽载荷随着啮合点在啮合线上的位置变化而变化，并与载荷分配系数S(x)相关［16］，其关系式为：

式中：b为有效齿宽，x、xI、xH、xQ、xS为啮合点坐标.

求得赫兹应力沿啮合线分布情况如图3所示.

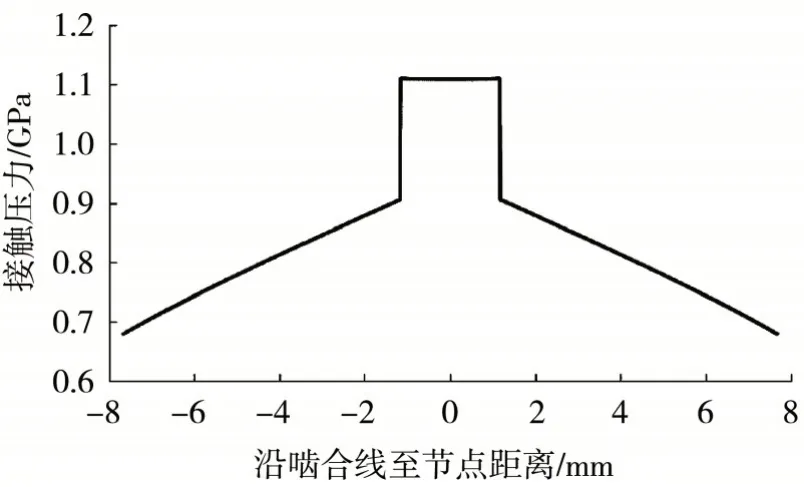
图3 赫兹应力沿啮合线分布图

1.2.3 滑滚比计算

由几何关系，可求得点K与两齿轮旋转中心O1、O2的距离分别为：

与间夹角的大小φ为：

式中：a为两齿轮中心距的大小.

齿轮1 和齿轮2 在点K处的速度大小分别为：

点K处齿面相对滑动速度、卷汲速度分别为：

其数值大小可由下式求得

联立上式滑滚比即为：

求得沿啮合线上摩擦因数μ的分布情况如图4 所示，当啮合点在节点附近时，齿面摩擦因数趋向于0，且单双啮合区交替时，摩擦因数会发生突变.

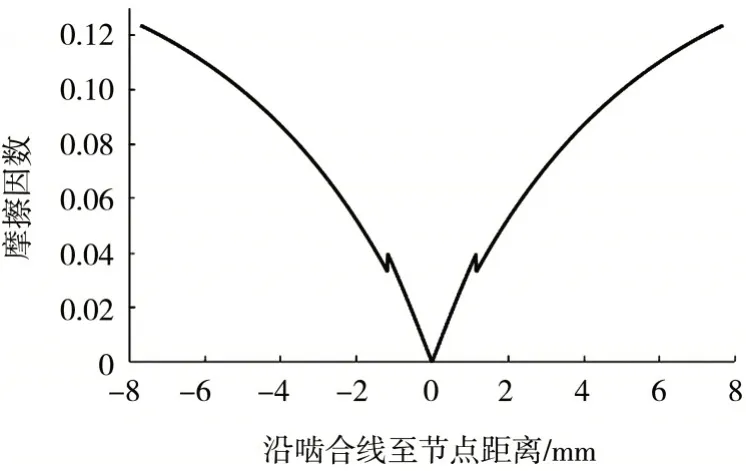
图4 渐开线齿轮摩擦因数沿啮合线分布图

1.3 渐开线齿轮的传动效率

由式（4）可知，啮合点在啮合线上移动一段距离de的时间内，齿间摩擦力所做的摩擦功为dA'，故齿间摩擦力在齿轮啮合期间所做的摩擦功可用定积分方程表示.

IQ段内齿面法向载荷为Fn，HI和QS段内齿面法向载荷为Fn/2，摩擦因数μ和啮合点到节点的距离e为与啮合点坐标x相关的函数，则齿间摩擦力在齿轮啮合期间所做的摩擦功A'为：

而驱动力做的功为：

渐开线齿轮的传动效率为：

2 微线段齿轮传动效率计算与渐开线齿轮的对比

图5 为一对微线段齿轮的啮合示意图［18］.齿轮1 为主动轮，齿轮2 为从动轮，角速度分别为ω1、ω2. 由微线段齿轮的形成原理可知［8］，微线段齿轮的齿廓由无数条渐开线弧线构成，每一段弧线都基于不同的基圆生成，因此微线段齿轮的啮合线不是一条直线，而是如图5 所示的“啮合弧线”.齿轮在弧线左端L0点开始啮合，在弧线右端M0点结束啮合，微线段齿轮满足齿轮啮合基本定律，即弧线L0M0通过节点P.

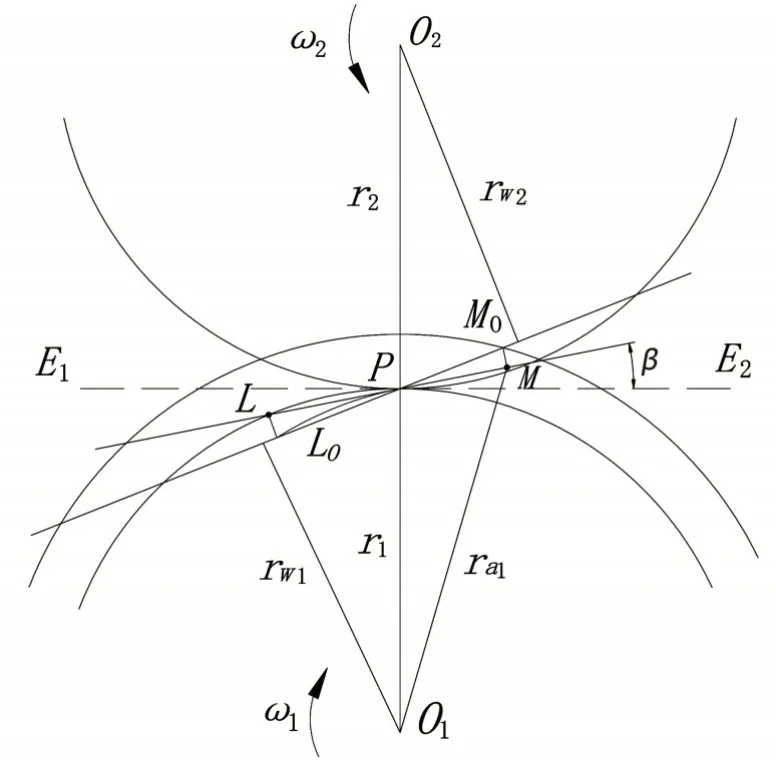
图5 微线段齿轮啮合示意图

设过节点P的水平直线为E1E2，为研究微线段齿轮在啮合过程中的摩擦功，现将啮合弧线上每一点投影至直线L0M0与直线E1E2夹角的角平分线上，该直线即为该对微线段齿轮啮合弧线的等效啮合直线，L0点、M0点在该直线上的投影分别为L点、M点.

如图6 所示，以节点P为原点，沿等效啮合直线为正方向建立x轴坐标系.其中LR和UM为双啮合区，RU为单啮合区，齿距ρe= πm.

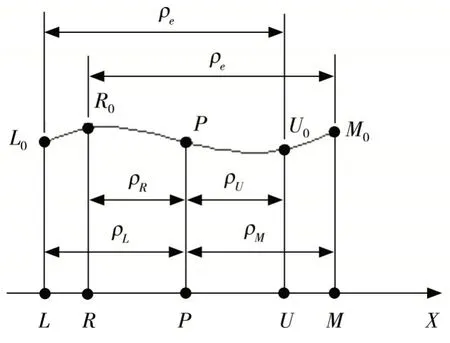
图6 微线段齿轮摩擦因数沿啮合线分布图

根据微线段齿轮原理，图1 中PK之间的距离e在微线段齿轮中为点K的曲率半径ρ，而微线段齿轮齿廓上第k点曲率半径的计算公式为：

式中：ρk为第k点的曲率半径，ρ0为初始基圆半径，rbi为第i个基圆的半径，δ为压力角增量.

通过编程可求出微线段齿轮齿廓每一点的曲率半径，其中得到的最大曲率半径即为ρL，且ρL=ρM.

则等效啮合直线上五点在该坐标系上的坐标分别为：

等效啮合直线LM与水平直线E1E2的夹角β，即为微线段齿轮的等效压力角，其公式为：

式中：ri、rai分别为微线段齿轮的节圆半径和齿顶圆半径，其计算公式与标准渐开线齿轮一致.

分别取O1点、O2点到拟合啮合线的距离为rW1、rW2，计算公式为：

根据以上微线段齿轮参数，结合用于渐开线齿轮的计算方法，可求得微线段齿轮啮合时摩擦因数沿等效啮合直线的分布情况，与渐开线齿轮的对比如图7 所示.

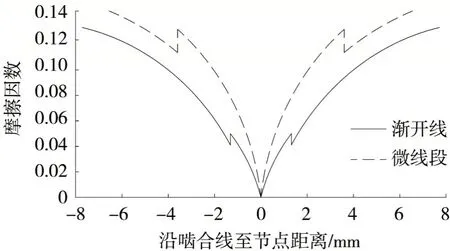
图7 渐开线齿轮与微线段齿轮摩擦因数分布对比

进一步地，微线段齿轮在啮合期间，齿面摩擦因数为μW，则齿面摩擦力所做的摩擦功为：

驱动力做的功为：

联立式（26）（27），微线段齿轮的传动效率为：

在不同的主动轮转速下，渐开线齿轮与微线段齿轮的传动效率η对比如图8 所示.可以看出，在齿轮共有参数完全相同的情况下，微线段齿轮的传动效率高于渐开线齿轮.

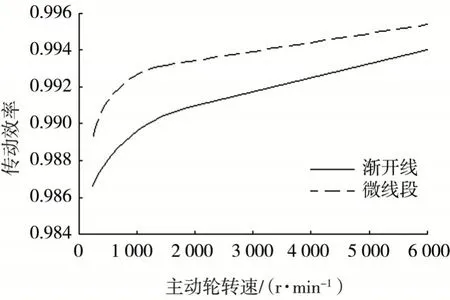
图8 渐开线齿轮与微线段齿轮传动效率对比

上文所述为齿轮外啮合传动效率的计算方法，同理可推得齿轮的内啮合传动计算方法.

3 3Z-Ⅰ型行星轮系传动效率计算

本文以3Z-Ⅰ型行星轮系为例，分别对其在采用渐开线齿轮和微线段齿轮的条件下进行传动效率的计算和对比，其结构如图9 所示.

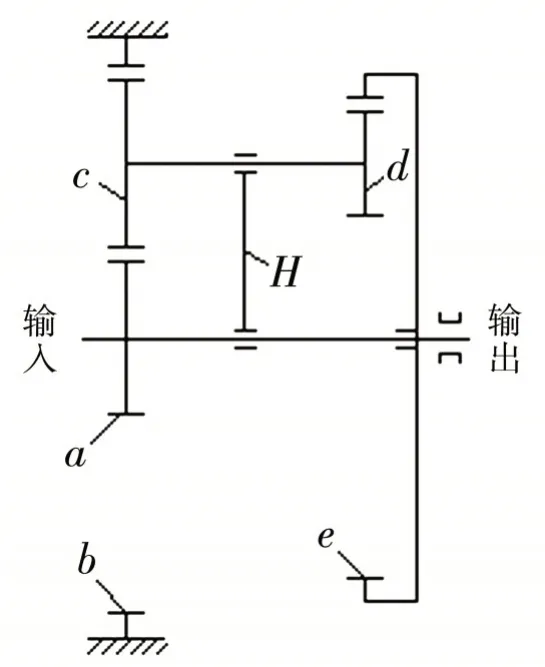
图9 3Z-Ⅰ型行星轮系结构原理图

由3Z-Ⅰ型行星轮系原理可知［19］，zi为齿轮i的齿数，为齿轮i的节圆直径，为齿轮i和齿轮j啮合传动时的传动效率，为齿轮i和齿轮j间相对于k的传动比.当＞，b轮固定，a轮输入，e轮输出时，该行星轮系的传动效率公式为：

其中可由上文中的方法计算求得，的计算公式为：

式中：为齿轮a和齿轮b间相对于行星架H的传动比.

齿轮的传动效率受到齿轮转速和转矩的影响，轮系中各齿轮的转速为：

式中：nb、nc、ne、nH分别为齿轮b、c、e和行星架H的转速.

转矩为：

式中：Ta、Tb、Te分别为齿轮a、b、e的转矩.

考虑到滚动轴承的摩擦损失，取轴承效率μn= 0.98，可得3Z-Ⅰ型行星轮系的传动效率为：

该轮系中各齿轮参数如表1 所示：微线段齿轮特有参数如表2 所示.

表1 行星轮系齿轮参数

表2 微线段齿轮参数

图10 为3Z-Ⅰ型行星轮系效率的求解对比结果.从对比结果中看出，微线段行星轮系的传动效率高于渐开线行星轮系传动效率η，约高5.3%.

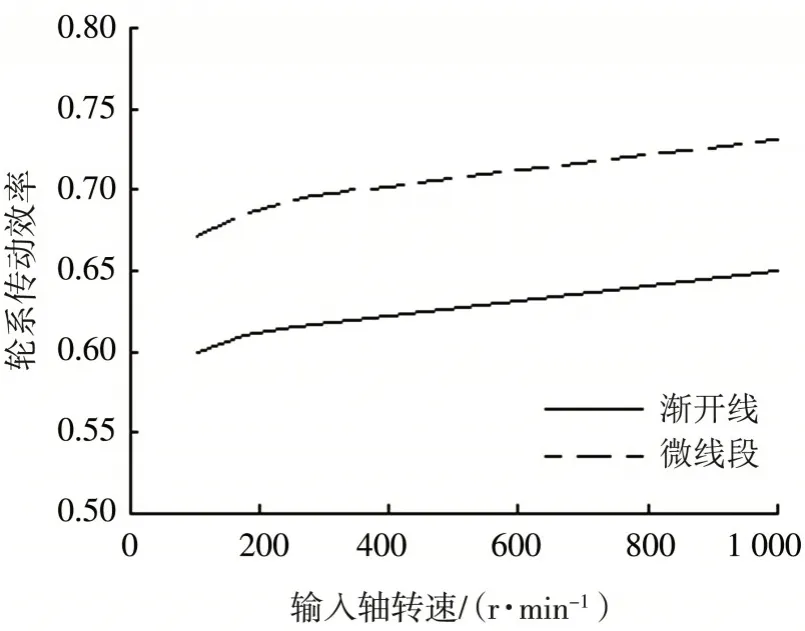
图10 渐开线轮系与微线段轮系传动效率对比

4 实验验证

通过理论计算可知，3Z-Ⅰ型微线段轮系传动效率高于渐开线轮系，特此进行实验验证.实验用3Z-Ⅰ型行星减速器如图11 所示，其减速比为99，各齿轮参数如表1、表2 所示，其余各参数均相同.

图11 渐开线齿轮与微线段齿轮行星减速器

行星减速器效率测定实验台如图12 所示，电机、转矩转速传感器A、被测减速器、转矩转速传感器B、摆线针轮减速器、磁粉制动器在底座上依次相连，进行实验.实验台运行时，记录转速转矩传感器A 和B 所显示的参数，进而计算出减速器的传动效率.由于磁粉制动器可施加的负载限制，故增加一摆线针轮减速器作为加速器以加大负载.

图12 行星减速器效率测定实验台

实验所用的电机为变频调速电机，可通过调节输入频率控制电机转速，磁粉制动器作为加载器，通过调节输入电流控制其所施加的负载.

分别对渐开线齿轮减速器和微线段齿轮减速器进行不同转速、不同负载下传动效率实验，实验结果如图13、图14 所示.

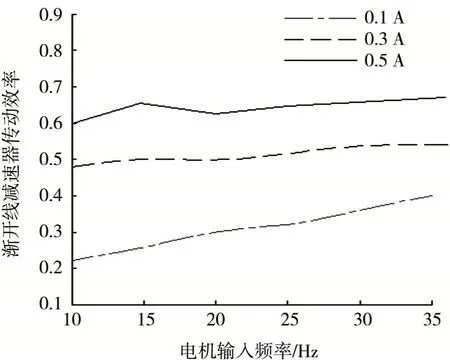
图13 渐开线齿轮行星减速器传动效率

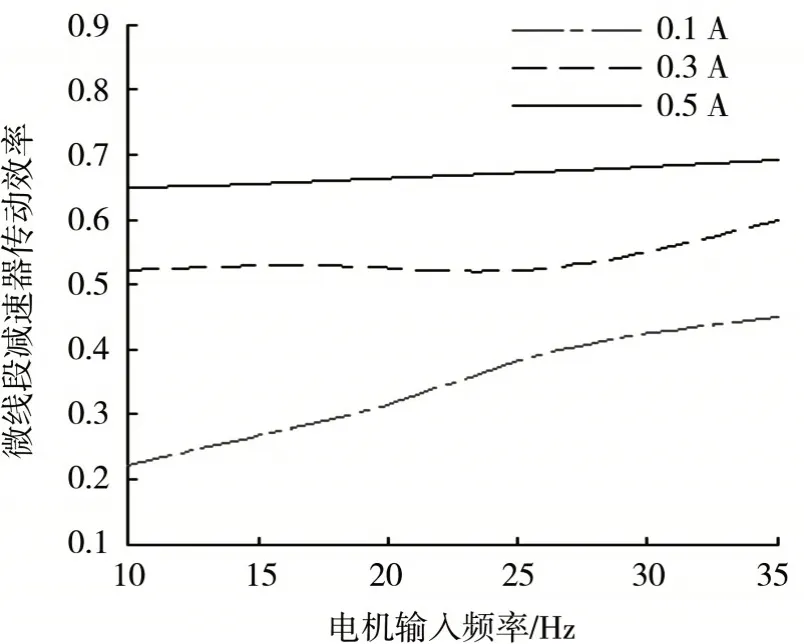
图14 微线段齿轮行星减速器传动效率

由于加工误差、装配误差、实验台误差和测量误差等因素的影响，实际测量结果与理论计算值有所偏差，但由实验结果可知，在相同条件下，3Z-Ⅰ型微线段轮系传动效率要高于渐开线轮系传动效率.

5 结论

利用摩擦功理论，推导出了考虑时变摩擦因素下渐开线齿轮的效率公式，并将此方法运用至微线段齿轮的计算.

参数条件相同的情况下，微线段齿轮传动效率高于渐开线齿轮传动效率，这与已有实验结论相符.

微线段齿轮可实际运用于行星轮系中，且传动效率高于相同参数的渐开线轮系.3Z-Ⅰ型行星轮系传动效率受输入轴转速和输出负载影响，输入轴转速越快、输出负载越大，轮系的传动效率越大，微线段轮系和渐开线轮系受此两点影响的结果相差很小.