基于单快拍MUSIC与改进UTJDL的海杂波抑制算法

韩文强,李庆忠,牛 炯

(1. 中国海洋大学 工程学院, 山东 青岛 266100)

(2. 联想集团 摩托罗拉移动通信技术有限公司, 湖北 武汉 430223)

0 引 言

船载高频地波雷达(HFSWR)[1]具备很强的灵活机动性,有效扩大了雷达的探测范围,广泛用于监测开放海域的舰船目标。对于船载HFSWR,由于海浪与平台运动的相互作用,海洋回波特性相对于岸基HFSWR更加复杂,前向运动会引起回波多普勒谱中的一阶海杂波展宽,导致展宽域中的目标被掩盖[2],对位于展宽域中的低速小目标检测非常不利。此外,在海浪的作用下,船载平台的六自由度周期性运动会在多普勒域产生附加峰,同样会影响目标的检测性能。因此,船载HFSWR的关键技术就是如何有效抑制展宽的海杂波和六自由度运动产生的附加峰,以实现对目标多普勒频率和方位的快速、准确检测。

目前船载HFSWR的目标检测方法主要包括运动补偿方法[3],基于预测相消模型(PC)的时域滤波算法[4],空域中的波束形成(DBF)方法[5-6]、正交加权(OW)方法[7]、斜投影(OP)[8]算法,以及空时自适应处理(STAP)[9]方法等。此外,利用深度学习技术进行海杂波抑制和海面目标检测也是目前研究的一个热点,如文献[10]提出了一种基于INet的导航雷达图像杂波抑制和海面动目标检测方法,并利用实测数据测试和验证了模型检测海面动目标的实时性和准确性,取得了较好的检测效果,但尚未考虑船载平台复杂运动对海杂波的影响。在以上诸多方法中,目前最有前景的方法是降维STAP方法,其中局域联合处理(JDL)[11]算法是目前的研究热点。

传统JDL算法在估计杂波协方差矩阵时,要求不同距离单元之间,海杂波应服从独立同分布。但对于船载HFSWR,由于船载平台前向运动会引起回波入射角随时间的变化,且不同距离元的回波入射角变化规律不同,导致不同距离单元间海杂波的分布特性不同[12-13],因此利用传统JDL算法估计杂波协方差矩阵时,就会出现估计精度恶化的问题。为克服这一问题,出现不少改进JDL算法。如文献[14]提出了一种利用距离维相关性系数加权的改进JDL算法,在估计被测距离单元杂波协方差矩阵时,通过相关系数确定训练样本的权重,以提高估计精度。文献[15]为了提高方位估计精度,首先利用多重信号分类(MUSIC)算法对待测距离单元进行方位处理,然后再利用JDL算法进行海杂波抑制,但MUSIC算法的精度需要大量快拍数据来支持,由于长时间相参积累导致快拍数过多,使其时间复杂度太高,或处理效率很低。对此,文献[16]提出一种单快拍MUSIC预处理的海杂波抑制算法,文献[17]提出一种高分辨稀疏表示的杂波抑制算法,但是以上方法对非均匀杂波抑制能力较差。此外,文献[14]利用无迹变换(UT)从单个距离单元的数据中,获得更多可用的训练样本,以粗略逼近感兴趣距离单元的杂波协方差矩阵。但是在其UT算法的矩阵计算中,要求被分解矩阵必须为正定对角矩阵,此条件在实际中往往无法满足,由此会造成滤波计算时存在较大误差[18]。

总之,改进JDL算法是目前最有前景的算法,但仍然存在两方面问题。一方面,为提高MUSIC算法方位估计精度,需要大量快拍数据集来支持,因此处理效率较低。另一方面,通过预处理来增加训练样本数据的UT算法,对分解矩阵要求过高而无法适应实际数据的特点。

针对以上改进JDL存在的两个问题,本文提出了一种单快拍MUSIC与改进UTJDL结合的海杂波抑制算法。为克服MUSIC算法需要大量快拍数据支持的问题,本文首先通过单快拍MUSIC算法得到不同距离单元的角度-多普勒数据,以实现对信号源的精准估计;然后,利用基于奇异值分解(SVD)的方法对UT算法中的矩阵计算进行了改进,避开了对分解矩阵要求苛刻的条件,并利用改进的UT方法对每个距离元的JDL数据进行预处理,从而获得更多的一致性数据;最后,根据不同距离单元与待检测距离单元的相关系数估计待测距离单元的协方差矩阵,并由此实现对海杂波的快速有效抑制。

1 单快拍MUSIC与改进UTJDL结合的海杂波抑制算法

根据以上分析,本文提出的船载海杂波抑制算法的整体流程如图1所示。该算法主要由两个模块组成,一是利用单快拍MUSIC算法,大大降低了传统MUSIC算法对过多快拍数的依赖,并实现了对目标角度的准确估计;二是利用基于SVD的UT算法解决了传统UT算法中非正定矩阵导致的滤波发散问题。下面具体介绍各个模块的具体实现过程。

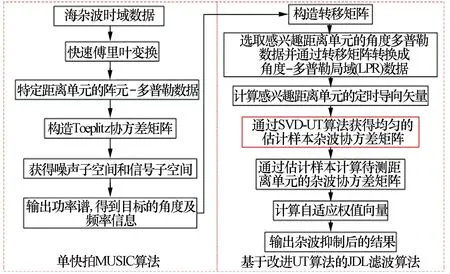
图1 海杂波抑制算法流程图

1.1 单快拍MUSIC算法

由于传统MUSIC算法的性能受快拍数的影响较大,快拍数越多,波达方向(DOA)估计越准确,但是大的快拍积累会造成很大的运算量,不利于实际工程应用[19],因此本文利用单快拍MUSIC将阵列信号转换成角度多普勒域的信号,进而再利用后续的滤波算法进行杂波抑制,在保证DOA估计精度的同时,可以大大降低运算量。单快拍MUSIC算法步骤如下:

(1) 通过构建Toeplitz矩阵[20]得到式(1)所示的协方差矩阵。

(1)

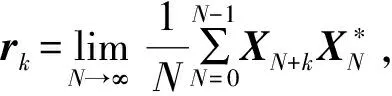
(4) 根据MUSIC算法谱估计公式[19]进行谱峰搜索。

根据以上步骤即可将阵列信号转换到角度多普勒域,得到输入数据PMUSIC。在特定的频率上,峰值最大处即对应着目标所处的方位。

1.2 基于SVD的UT算法

UT是一种采用确定采样策略逼近非线性分布的统计信息的方法[18]。其原理是根据输入变量的均值和方差,使用一定规则和数量的样点集称作Sigma点,用于模拟输入变量的分布,然后将Sigma点代入非线性系统,得到相应的输出点集,从而得到估计的均值和方差。

由于传统UT算法在计算Sigma点时需要用到Cholseky分解,其前提条件是被分解矩阵必须为正定对角矩阵,此条件在实际中往往无法满足,由此造成滤波计算时存在较大误差。因此,本文采用基于SVD的UT算法。对于船载HFSWR数据,假设距离单元r处,ηa×ηb维大小的角度-多普勒局域(LPR)数据经过向量化处理后得到ηaηb×1维数据xLPR,其均值和协方差分别为mx和Rx。通过均值mx和协方差Rx可以获得2ηaηb+1个Sigma点及相应的权值,即

(2)

(3)

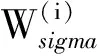
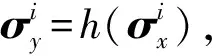
(4)

(5)

在以上步骤中,SVD在矩阵负定时依然能够正确分解,表现出比Cholseky分解更好的稳定性[18,21]。

1.3 基于单快拍MUSIC和改进UTJDL的海杂波抑制算法

本文提出的船载HFSWR海杂波抑制算法主要由以下步骤组成。

(1)利用单快拍MUSIC算法把阵列-距离-多普勒数据转换为距离-角度-多普勒域数据PMUSIC。如图2所示,将PMUSIC作为输入数据,选取PMUSIC距离r处的角度-多普勒数据,选取大小为ηa×ηb的LPR数据xLPRr,并将数据进行向量化。

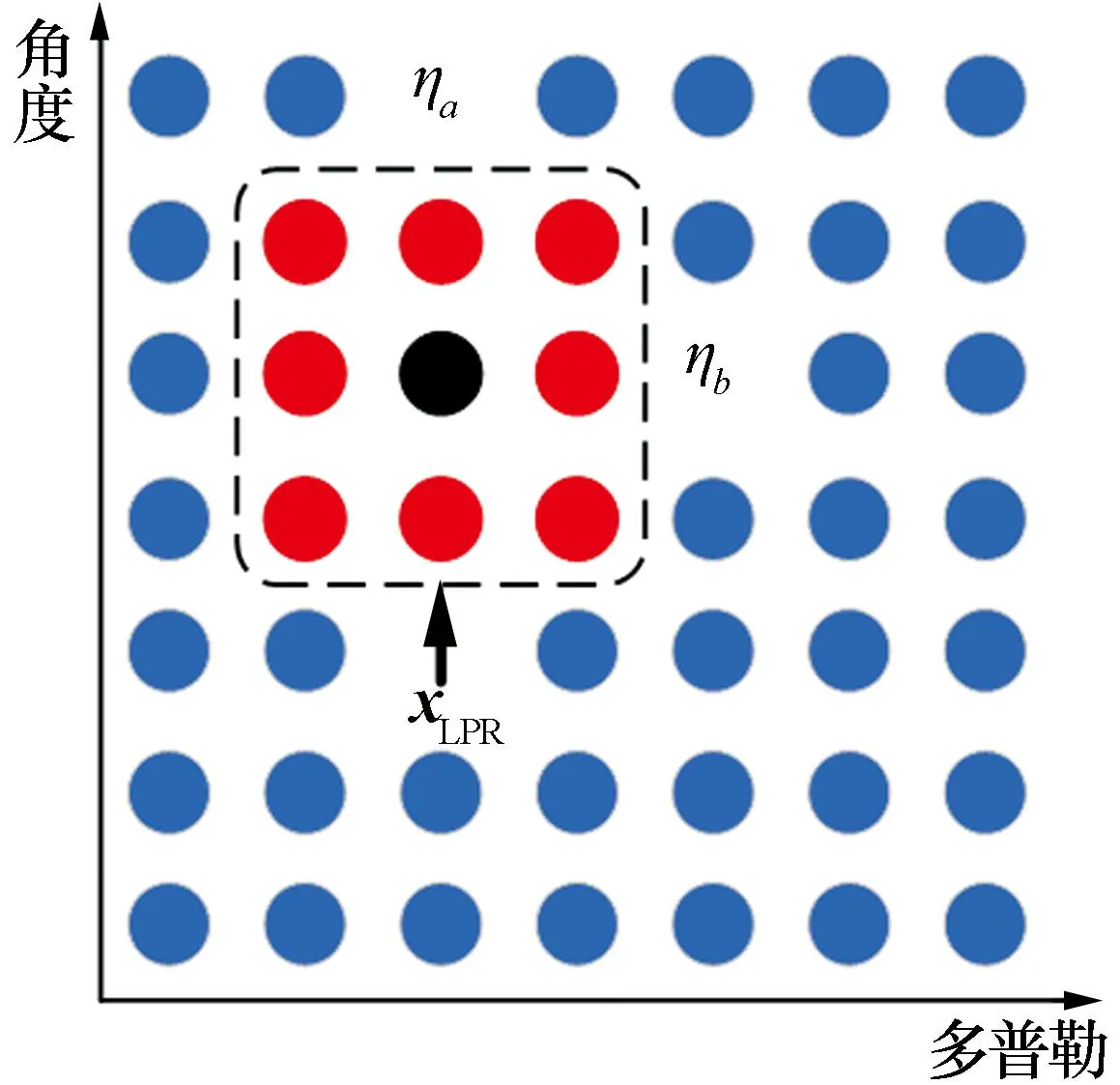
图2 改进JDL算法中的LPR

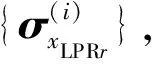
(3) 估计训练样本与待测距离单元之间的相关系数。为提高待测距离单元协方差矩阵估计的准确性,本文首先估计样本距离元与待测距离单元之间的相关性,具体步骤如下:

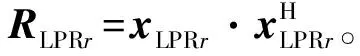
步骤2 对RLPRr进行特征分解,然后选取最大特征值对应的特征向量,将选取的特征向量进行归一化后记作ζr。

步骤3 对于训练样本所在的距离单元,重复步骤1、步骤2,得到对应的ζi。

(4) 通过式(6)获得待测距离单元的协方差矩阵。

(6)

式中:ρi表示第i个距离单元的估计样本与待测距离单元之间的相关性系数;Ryi为第i个距离单元通过改进UT算法获得的估计样本协方差矩阵。

(5) 构建转换矩阵Tst和LPR内的空时导向矢量。

Tst=[hv⊙st(f-1),hv⊙st(f0),hv⊙st(f1)]⊗

[ss(φ-1),ss(φ0),ss(φ1)]

(7)

式中:Tst转换矩阵由空间导向矢量和时间导向矢量进行Kronecker积得到;st(φ)为输入数据的时间导向矢量;ss(f)为输入数据的空间导向矢量;hv为汉宁窗。

根据式(8)即可获得LPR内的空时导向矢量

(8)

其中

s=st(f0)⊗ss(φ0)

(9)

式中:s为单个距离单元空时数据的空时导向矢量。

(10)

利用自适应权值向量可以获得修改的样本矩阵求逆(MSMI)统计量

(11)

该统计量即代表特定角度-多普勒单元的估计值。为了获得全部角度-多普勒区域的估计值,通过对角度和多普勒进行遍历,即可达到在角度-多普勒域进行杂波抑制的目的。

2 实验结果与分析

为验证本文算法对船载HFSWR一阶海杂波及附加峰的抑制效果及目标检测的准确性,本文利用仿真数据和实测数据对提出的算法进行了实验验证,并与其他杂波抑制算法进行了性能比较。

本文采用信杂噪比(SCNR)[12]作为评价指标,衡量各种算法对海杂波的抑制效果。杂波抑制前后SCNR的提升量SCNRimprove越大,代表杂波抑制效果越好,反之则抑制效果越差。杂波抑制前后SCNR提升量为

SCNRimprove=SCNRafter-SCNRbefore

(12)

(13)

式中:Ps表示感兴趣多普勒单元处信号的功率;Pc+n表示杂波加噪声的功率。

2.1 仿真海杂波抑制实验结果

本节根据文献[12]提出的海杂波模型对海杂波三维数据进行了仿真。表1给出的是仿真模型所用参数,其中d为阵元间距,M为脉冲积累个数,N为阵元数目,A1和A2都是瑞利分布随机变量,λ为雷达波长,Tr为脉冲重复周期,fc为雷达发射信号载波频率,Vp表示船前向行驶速度,rmax表示雷达最大探测距离。表2给出的是三自由度摆动运动的相关参数。为了更好地对海杂波进行仿真,在仿真模型中加入了20 dB的高斯白噪声。

表1 模型参数列表

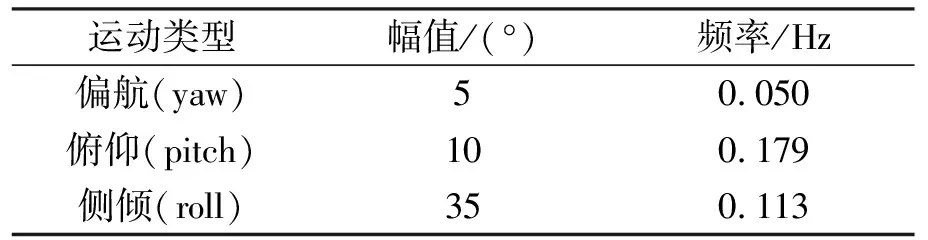
表2 三自由度摆动参数

当船载平台速度Vp=4 m/s时,海杂波仿真结果如图3所示,其中图3a)为得到的距离-多普勒(RD)谱,图3b)为角度-多普勒(AD)谱,图3c)为仿真目标所在距离单元的多普勒截面。可见,当船载平台前向运动时,一阶海杂波展宽严重,目标被掩盖在展宽的一阶海杂波之中。因此,船载海杂波的抑制是实现目标准确检测的关键。

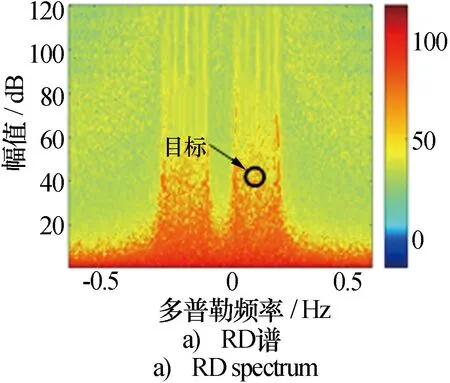
图3 海杂波数据仿真结果

图4是本文算法与DBF[5]、JDL[11]及UTJDL[12]算法对仿真海杂波抑制与目标检测的AD谱对比结果。当船载平台速度Vp=4m/s时,本文分别在距离为50 km,方位角为60°,频率为-0.318 0 Hz和0.176 7 Hz处添加两个目标。此外,仿真目标的输入SCNR均为-30 dB。

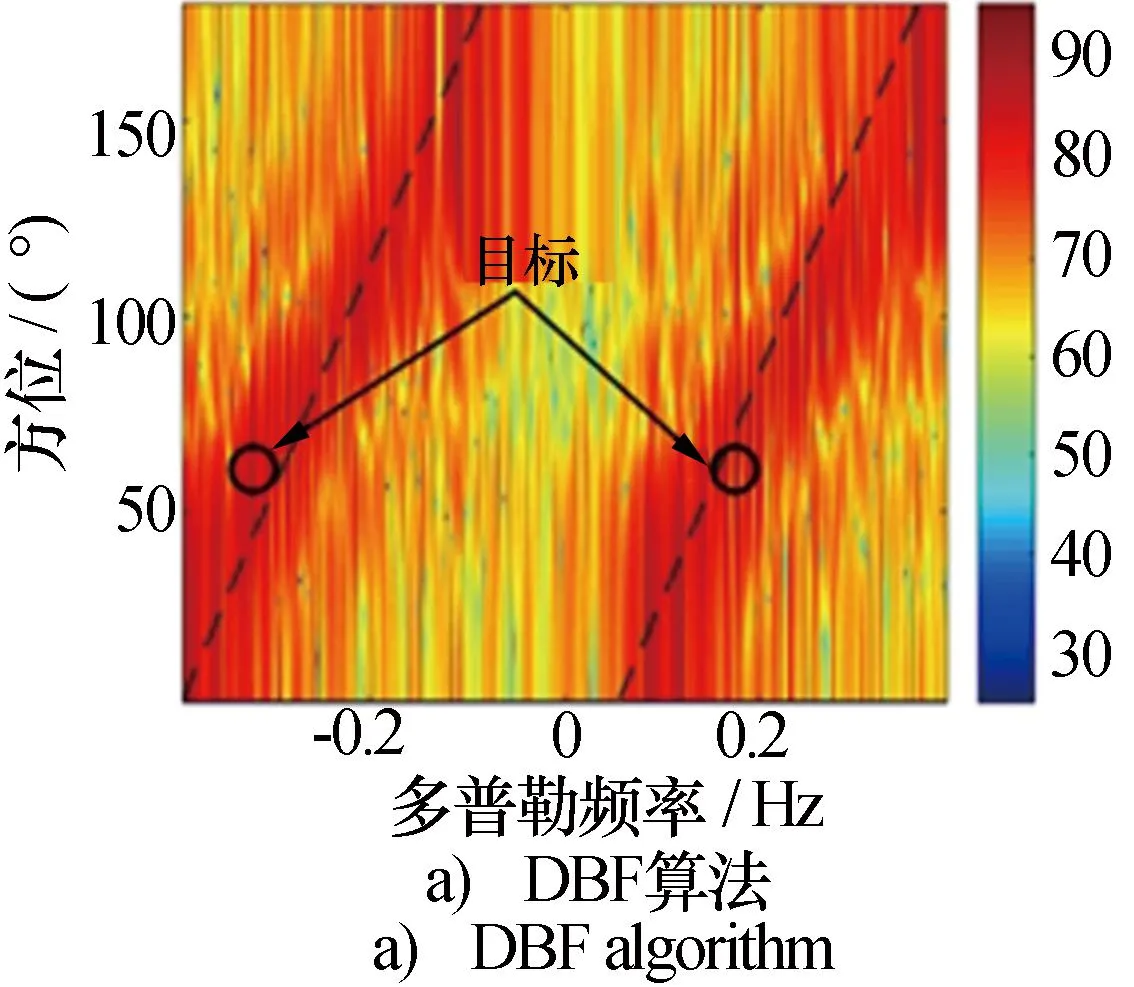
图4 仿真海杂波抑制结果

图4a)是DBF算法处理后的结果,可以明显看到一阶海杂波展宽非常严重,目标被掩盖在展宽的一阶海杂波之中,该方法对海杂波抑制效果很差;图4b)是JDL算法的抑制结果,该算法对展宽的一阶海杂波有一定的抑制作用,但是仍然有残留的杂波,不利于后续目标的检测;图4c)为UTJDL算法的处理结果,可以看出,大部分海杂波都被滤除,但目标方位、幅值不高,仍有可能受到杂波的干扰;图4d)为本文提出算法的处理结果,可以看出,本文算法对海杂波有很好的抑制作用,并且舰船目标在AD谱中很容易准确定位。

下面分别从海杂波抑制及目标方位检测误差两方面,进一步考察以上四种算法的性能好坏。图5为目标所在方位的多普勒截面曲线,从中可见,本文方法对海杂波抑制效果最好,且本文算法的多目标检测能力最佳,因为目标1和目标2的分辨率都是最高的。图6为目标1所在频率的方位截面曲线,目标方位位于60°,从中可见,本文方法测得的目标准确度最高,并且最高幅值不受其他角度的影响,本文算法明显优于JDL以及UTJDL算法。这主要是因为单快拍MUSIC算法通过预处理提高了角度估计的精度,并且改进的UT算法能够获得更均匀的次要数据,使得感兴趣距离单元杂波协方差矩阵的估计精度提高。

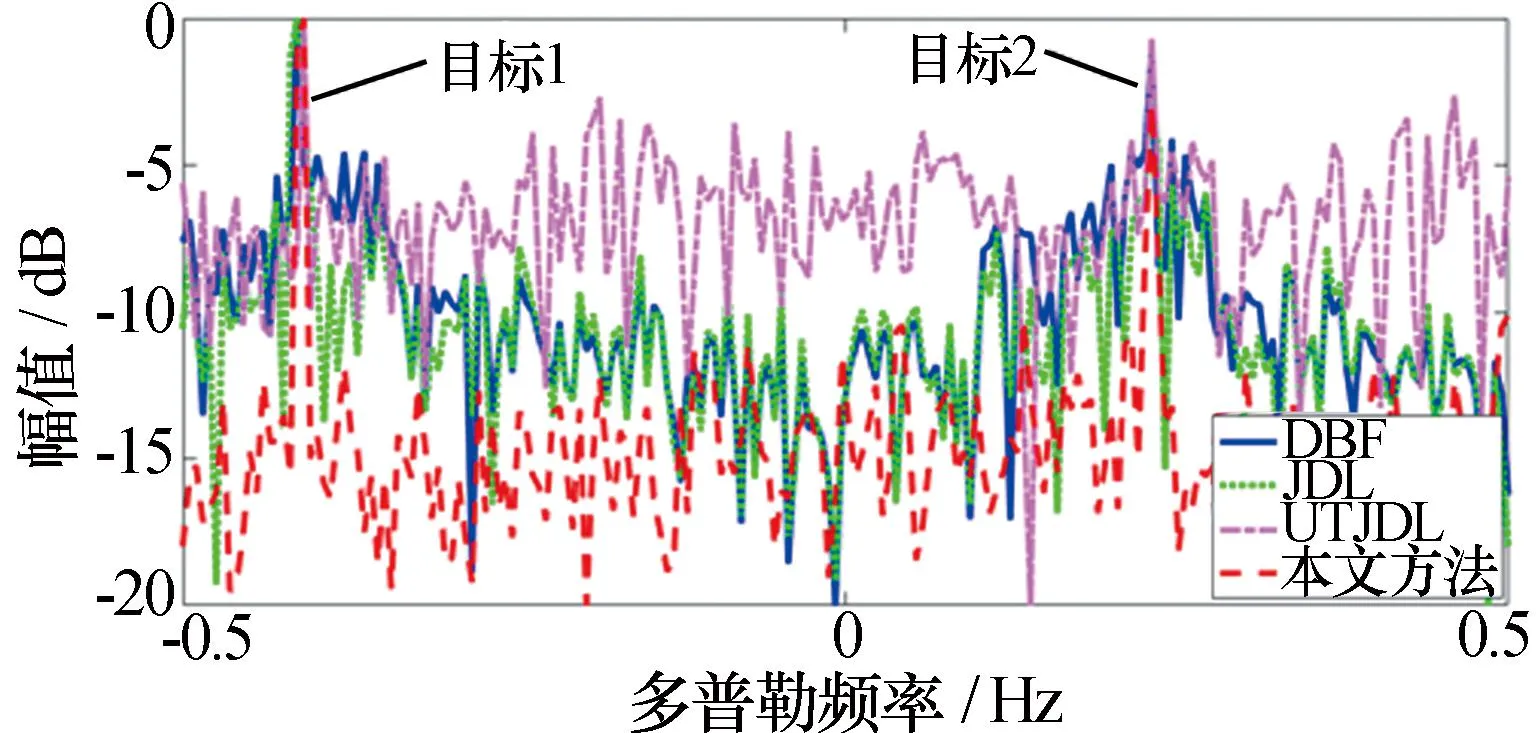
图5 四种算法海杂波抑制性能对比

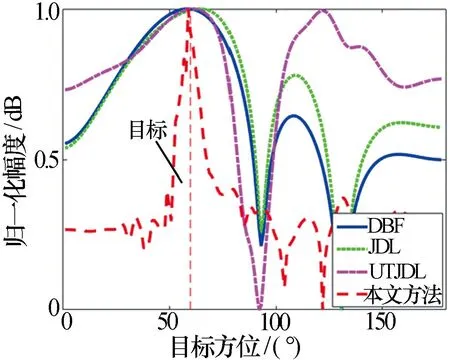
图6 四种算法目标方位检测精度对比

表3给出了四种算法经过100次蒙特卡罗实验后检测到的目标最大幅值与杂波差的平均值ΔA、输出SCNR的平均值以及SCNR平均提升量。由表3可知,本文算法SCNR提升量最高,在杂波抑制后目标更容易被检测到。

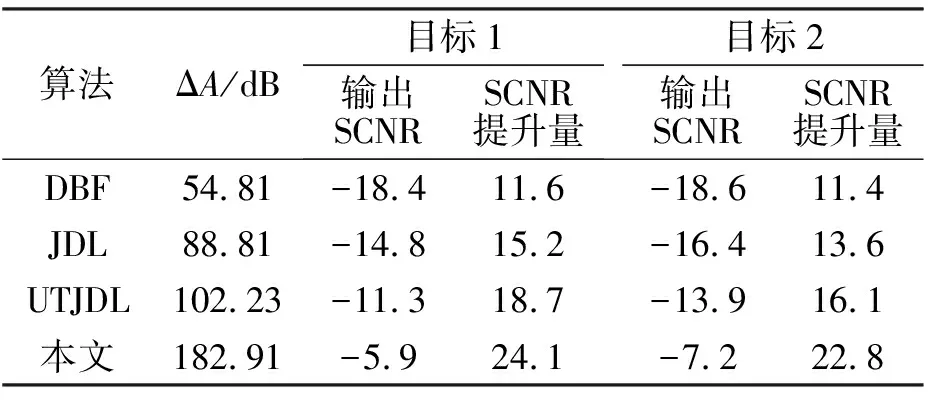
表3 四种算法海杂波抑制性能对比表

2.2 实测海杂波抑制结果

为进一步验证算法的性能,下面利用中国海洋大学威海移动站于2019年7月20日7时51分测得的海杂波数据进行实测。本文在实测数据中添加两个距离为40km,角度为60°,频率分别为-0.1106Hz和0.398 2 Hz的仿真目标,仿真目标的输入SCNR为-30 dB。图7为DBF、JDL、UTJDL及本文算法对实测数据的处理结果。由于实测数据受到天线方向图误差的影响,无论是目标信号还是海杂波都会被其来向所对应的天线误差加权[22],因此DBF算法的结果最差,而本文算法AD谱中目标分辨率最高,并且很容易分辨目标所处方位。

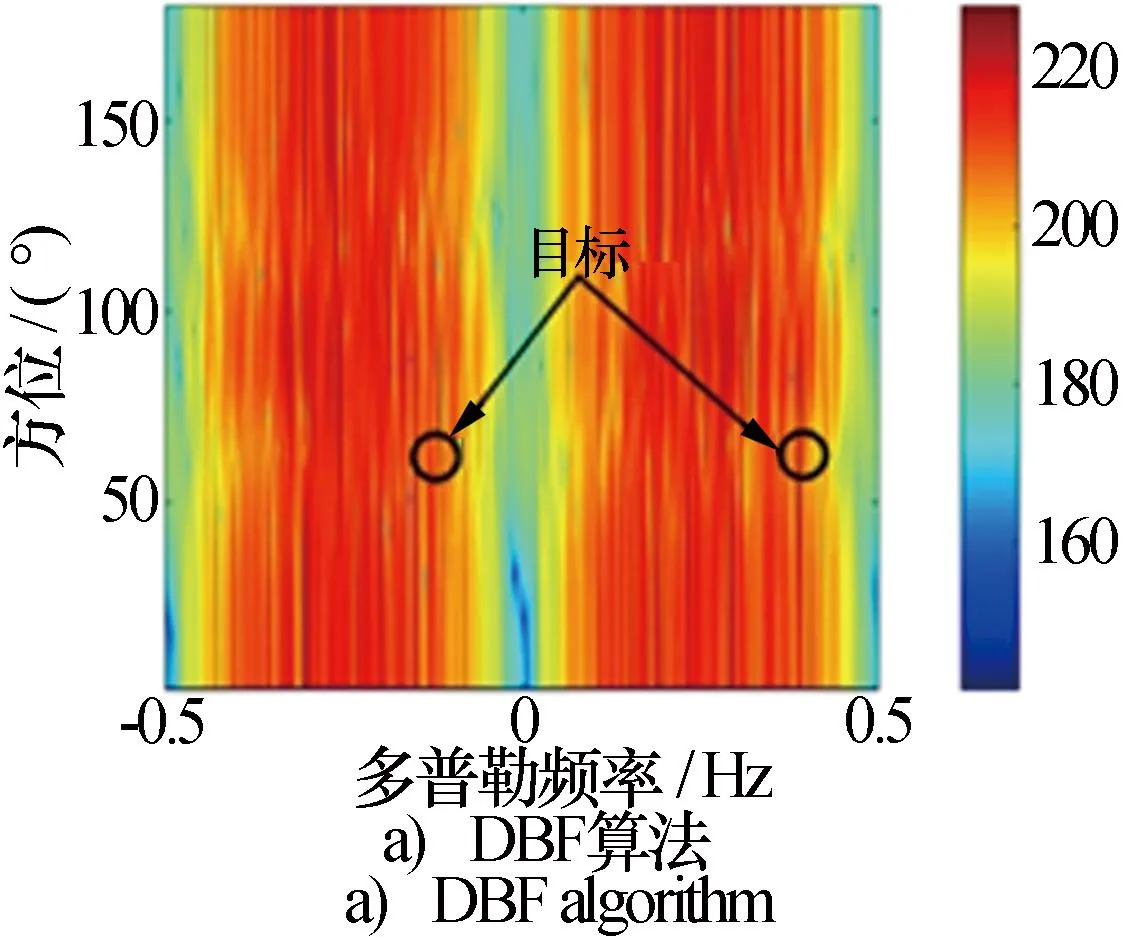
图7 实测海杂波抑制结果

图8为实测数据在四种算法抑制后目标所在角度为60°的多普勒截面,可见对于实测数据,本文算法不仅能抑制杂波,还能使目标分辨率最高。图9为实测数据在四种算法抑制后目标所在频率的角度估计,相较于传统算法,本文算法检测精度最高。

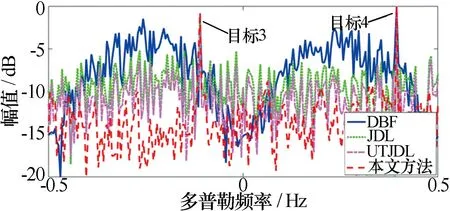
图8 四种算法对实测海杂波抑制性能对比

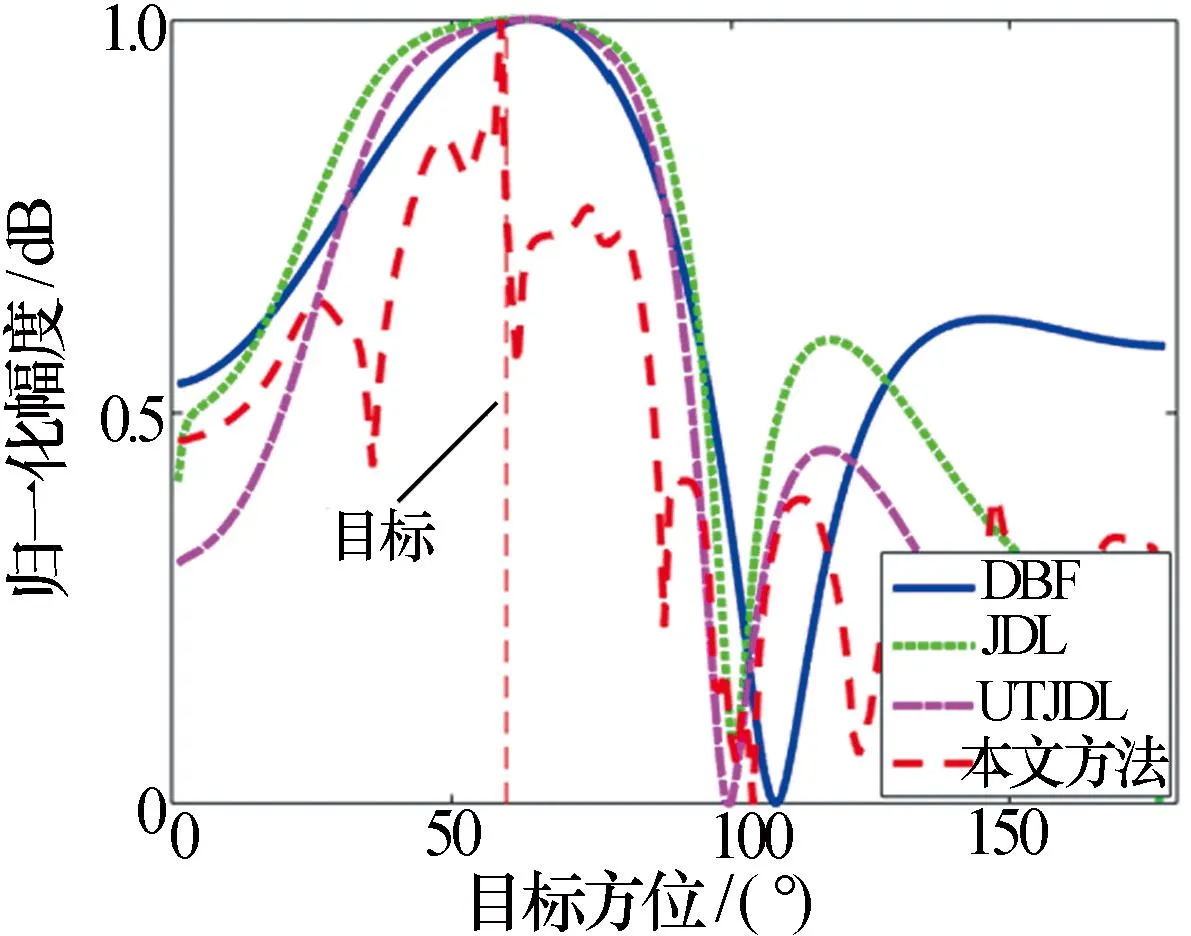
图9 四种算法对实测数据目标方位检测精度对比

表4展示了实测数据在四种算法处理后的目标幅值与杂波最大差值的平均值以及输出SCNR的平均值,从中可见,本文算法在实测数据处理时一阶海杂波背景被很好地抑制,目标幅值与海杂波最大差值的平均值最大,并且输出的SCNR最大,海杂波抑制前后SCNR提升量最大。

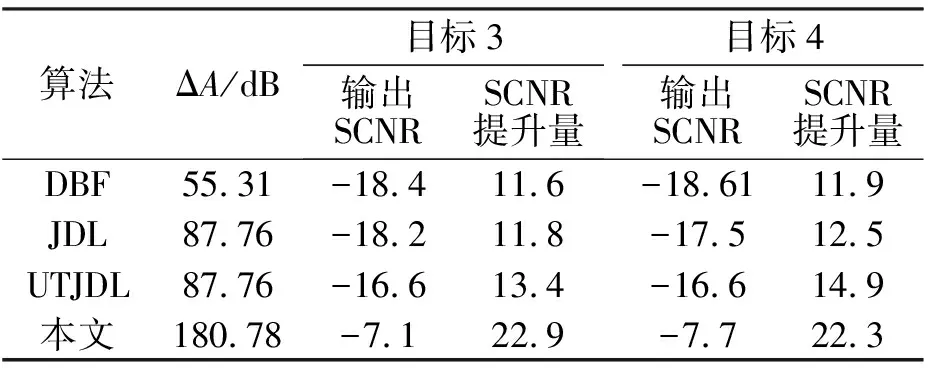
表4 四种算法对实测海杂波抑制性能对比表

2.3 算法运算量分析

本节将分析改进算法的运算量。假设雷达阵列为均匀线性阵列,阵元数为N,脉冲积累个数为M,距离单元数为r,下面分别从单快拍MUSIC算法及基于改进UT算法的JDL滤波算法两部分分析运算量。

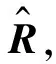
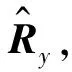
(14)

根据式(14),利用实测数据中的参数取值M=1 024,N=7,ηa=ηb=3,r=23,得到改进算法的总运算量约为1.610 96×1010次浮点运算。因此,本文算法计算量的降低主要在体现在单快拍MUSIC算法的应用上。

3 结束语

针对传统海杂波抑制算法对非均匀海杂波抑制能力不足以及现有优化方法存在局限性的问题,本文提出了一种单快拍MUSIC与改进UTJDL结合的船载HFSWR海杂波抑制与目标检测算法。利用单快拍MUSIC可以提高目标角度估计的准确率和处理效率,通过SVD分解可以解决传统UT算法中非正定矩阵导致的滤波发散问题。利用改进的UT算法可以获取均匀的估计样本,解决了传统JDL算法需要不同距离单元服从独立同分布的问题。此外,利用不同距离元之间的相关性系数对估计样本的协方差矩阵进行加权,可以提高协方差矩阵估计的准确性。从仿真数据和实测数据的实验结果可以看出,与传统算法相比,本文算法对同角度不同频率的多目标检测能力最佳,目标角度、频率的估计都较为准确,且信杂噪比提升最大。

此外,本文算法不仅适用于船载HFSWR海杂波抑制,还适用于所有均匀训练样本有限的情形。本文提出的杂波抑制算法是一种解决非均匀杂波问题的有效方法,对复杂环境下目标和杂波的适应性较强。然而,本文算法无迹变换采用线性变换代替非线性变换,如何找到一种合适的非线性变换是今后的研究重点。另外,由于实测目标距离单元未知,今后研究中可以搭配船舶自动识别系统,先确定目标信息后再进行实测海杂波抑制,这样能更好地验证本文算法对未知海杂波的抑制能力。