基于二维阈值SL0范数算法的压缩感知ISAR成像
史润佳,黄一飞,蒋忠进
(东南大学 毫米波国家重点实验室, 江苏 南京 210096)
0 引 言
逆合成孔径雷达(ISAR)成像能提供目标的高分辨图像,在军事领域具有广泛的应用前景。非合作目标的ISAR图像是重要情报信息,快速成像甚至实时成像具有非同寻常的意义,因此,ISAR成像快速算法一直是研究热点[1-3]。ISAR成像中的一个关键步骤就是目标强散射点参数估计。用于实现参数估计的算法有很多,而压缩感知类算法是其中非常重要的一类[4]。
平滑l0范数(SL0)算法是压缩感知类参数重构算法的一种,由Hosein Mohimani等人于2009年提出[5]。此算法利用单峰函数组合来近似参数集的l0范数,比如高斯函数组合、三角函数组合和双曲线函数组合等,然后通过逐步优化来寻求参数重构的最优解。平滑l0范数算法解决了最小l0范数算法面临的多项式复杂程度非确定性(NP)问题,相比于基追踪(BP)算法[6]、梯度投影稀疏重构(GPSR)算法[7]和贪婪算法[8],平滑l0范数算法具有更快的运算速度。
为了改进平滑l0范数算法性能,文献[9]选取双曲正切函数组合来近似l0范数,并且采用修正牛顿法来代替最速下降法,很好地解决了迭代方向上目标函数值出现“锯齿”现象的问题,在拟合精度上得到了提升。但修正牛顿法对迭代初始值的选取比较敏感,为解决这一问题,文献[10]提出先使用最陡下降法计算出一个合适的初始值,再利用修正牛顿法获得最优解。除此之外,文献[11]提出了一种阈值SL0算法,该算法将每次迭代的效率指标与设定阈值相比较,以剔除某些低效的迭代,从而提高了参数重构效率。文献[12]选用了双曲正切函数与高斯函数的组合来代替单一的高斯函数组合,此函数“陡峭性”更强,提高了对离散l0范数的拟合程度。
近年来,平滑l0范数算法在雷达成像领域也得到很多研究和尝试。Armin Eftekhari等人于2011年提出了用于二维信号的2D-SL0算法[13],此算法可以直接应用于ISAR成像。文献[14]针对观测模型二维可分离的特点,提出了一种修正SL0算法,将ISAR回波信号二维解耦,从而对距离向和方位向分开进行重构。文献[15]将2D-SL0算法用于基于2D信号的 3D ISAR成像中,提高了3D图像的分辨率。文献[16]利用拉格朗日数乘法对ISAR回波信号进行了降噪预处理,然后采用2D-SL0算法进行ISAR成像,改善了成像效果。
本文采用平滑l0范数算法进行ISAR成像研究,并提出一种二维阈值平滑l0范数快速算法,此处简称2D T-SL0算法。该算法采用一种迭代效率指标来评定内循环迭代的有效性,并剔除迭代效率指标偏低的内循环。该快速算法在不影响ISAR成像效果的前提下,能减少大量的无效内循环迭代次数,以缩短ISAR成像时间。
1 ISAR成像模型
在很短的相干累积时间内,ISAR成像基本原理可等效为图1所示的二维转台模型。由于目标尺寸远远小于目标到雷达的距离,所以在对回波数据完成运动补偿及相位校正以后,目标上任意一个散射点σ(u,v)到雷达的距离可近似为

图1 ISAR成像二维转台模型
R(t)≈R0+usinθ+vcosθ
(1)
式中:u和v是散射点的坐标;R0是雷达到目标中心的距离;θ是目标转动的角度。
使用理想点散射中心模型,目标的谱域后向散射场可表示为
(2)
式中:f是入射频率;σd是散射点散射系数;D是散射点数目。
式(2)中,exp(-j4πfR0/c)为常数项,不影响各个散射中心之间的相位差,可将其省略。将雷达向目标发射信号的方位角离散为M个角点,第m个角点为θm,m=1,2,…,M。每个角点发射N个频率步进的脉冲,第n个频点为fn,n=1,2,…,N。由此,经推导可得第m个方位角的第n个频点的散射场
(3)
将二维成像场景离散成P行Q列。为使散射中心不发生越距离单元徙动,目标与雷达之间的相对转动角度一般很小,因此可以认为sinθm≈θm,cosθm≈1。由于在ISAR成像中,雷达脉冲带宽相对于中心频率很小,则可认为在频率变化时,波长近似不变。经过推导可得散射场表达式
(4)
将式(4)表示为矩阵形式,可得
Y=AXBT
(5)
式中:Y∈M×N,为回波信号的观测矩阵;X∈P×Q,为散射系数矩阵;A∈M×P,B∈N×Q,分别为方位向和距离向的感知矩阵,将其展开,则
(6)
(7)
2 压缩感知参数重构算法
2.1 常规2D-SL0算法
二维离散场景的网格点数P×Q远大于散射中心个数D,因此散射中心具有明显的稀疏性,可以利用压缩感知的参数重构算法,从观测信号中重构出各个散射中心的幅度参数,从而构建ISAR图像。
常规2D-SL0算法是一种压缩感知类参数重构算法,该算法用高斯函数组合来近似散射系数矩阵X的l0范数,得到连续可微的目标函数,避免了非连续函数最小化的NP难问题。该算法要解决的是一个优化问题,其优化目标为
(8)
式中:L(X)被用于近似散射系数矩阵X的l0范数,可表示为
L(X)=PQ-Fσ(X)=
(9)

常规2D-SL0算法需要内外两层循环。外循环里,预设K个σ值,并逐步减小σ值,使函数Fσ(X)的波形由光滑趋向于起伏;内循环里,使用最陡下降法求当前σ值下能使Fσ(X)增大的X值,但一共只迭代L次,以免陷入局部最优。当σ值趋于最小的时候,X收敛到全局最优值。
因此,常规2D-SL0算法需要预先设置外循环次数K和内循环次数L。在任一轮内循环里,不论参数优化的收敛效果如何,内循环次数都是设定的L次,这样僵化的迭代策略会导致效率低下。仿真结果表明,在某些轮内循环里,参数估计值只在前面若干次内循环里得到持续优化,在后续内循环里变化极其缓慢,甚至不变,此时的内循环属于无效迭代。因此,并不是每一轮内循环(即每一次外循环)都有运行L次迭代的必要。
2.2 2D T-SL0快速算法
在本文提出的2D T-SL0算法里,针对某个既定的σ值,或者某次既定的外循环,存在函数gσ(xp,q)为
(10)
将式(10)求导可得
(11)
在该次外循环里,设定L次内循环,且根据拉格朗日中值定理,得到
(12)
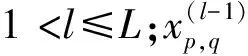
(13)
(14)
将式(14)写成矩阵形式,有
(15)
式中:“·”为点乘,即两个矩阵元素对应相乘,矩阵D(l-1)可表示为
(16)
对式(15)两边取l2范数,可得
(17)
然后有
(18)

(19)
此处定义误差统计量为
(20)
然后有
(21)
以及
(22)

E(l-1)=‖ΔX(l)‖2/c(l)
(23)
为了描述迭代效率,此处定义误差统计量E的相对变化率为
(24)
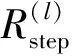
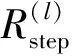
(25)
式中:I为从第一轮内循环开始,有效进行过的总迭代次数,即实际迭代次数,所以I会随着迭代的增加而变化。
2.3 ISAR成像步骤
2D T-SL0算法的具体实现步骤如下:
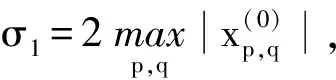

图2 2D T-SL0算法流程
3 实验结果及分析
本文对2D T-SL0算法进行了软件编程和ISAR成像测试,使用了仿真数据和实测数据,与常规2D-SL0算法、距离-多普勒(R-D)算法、旋转不变参数估计(ESPRIT)算法在计算时间与成像效果方面进行了比较。
仿真实验使用的目标模型为P-51飞机,其CAD模型如图3所示。电磁仿真的基本参数如下:发射信号中心频率为10 GHz,带宽为0.5 GHz,步进频采样,采样频点为64;俯仰角固定为75°;方位角范围为[-1.432 4°,1.432 4°],采样64个角点。仿真得到的回波二维谱矩阵的尺寸为64×64,对应的径向和横向分辨率均为0.3 m。实验使用主频3.20 Hz的中央处理器、64位Windows10操作系统。

图3 P-51飞机模型
为了验证2D T-SL0算法在剔除无效内循环迭代方面的效果,本实验首先统计并给出了2D T-SL0算法与常规2D-SL0算法的参数更新步长收敛对比结果,如图4所示,其横轴是实际迭代次数。由于在梯度下降法中,梯度趋于0即步长趋于0时达到收敛,故可用步长值随实际迭代次数的变化模拟算法的收敛效果。从图4可以看出,2D T-SL0算法中步长值下降更快,达到收敛前所使用的迭代次数明显少于常规2D-SL0算法。

图4 参数更新步长变化曲线
在内外循环次数K和L设置相同的情况下,由于2D T-SL0算法的实际迭代次数要远小于常规2D-SL0算法,所以2D T-SL0算法的ISAR成像速度也快于常规2D-SL0算法。表1和表2对比了两种算法在外循环分别设定为30次和50次时,ISAR成像的计算时间。从中可见,常规2D-SL0算法里,随着设定内外循环次数的增加,计算时间也相应增加。而在2D T-SL0算法里,由于剔除了无效迭代,随着设定内外循环次数的增加,计算时间变化很小,且在设定内循环次数较大时,计算时间明显低于常规2D-SL0算法。

表1 外循环30次的仿真时间对比

表2 外循环50次的仿真时间对比
在仿真数据的ISAR成像效果方面,实验比较了四种算法在信噪比分别为0 dB、5 dB、10 dB条件下的成像效果,其结果如图5所示。

图5 基于仿真数据的ISAR成像结果
从图5可以看出,R-D算法和ESPRIT算法成像的尺寸与回波二维谱矩阵的尺寸相同,都为64×64;而常规2D-SL0算法与2D T-SL0算法属于压缩感知类算法,散射系数矩阵的尺寸可以大于回波二维谱矩阵,本实验设定的散射系数矩阵X的尺寸为128×128。从ISAR成像效果来看,2D T-SL0算法要好于R-D算法和ESPRIT算法,与常规2D-SL0算法相当。
上述四种算法的成像时间比较如表3所示。2D T-SL0算法和常规2D-SL0算法均设定K=30,L=40。由表3可见,2DT-SL0算法快于常规2D-SL0算法;R-D算法基于快速傅里叶变换实现,成像时间最短;ESPRIT算法的成像时间最长。

表3 仿真数据成像时间对比
此外,本实验还采用实测数据进行了ISAR成像,实测数据来自于Yak-42飞机。发射信号的中心频率为5.52 GHz,带宽为0.4 GHz,脉冲重复频率为400 Hz,径向分辨率为0.375 m。上述四种算法对于实测数据的ISAR成像结果如图6所示。

图6 基于实测数据的ISAR成像结果
由图6可知,2D T-SL0算法的成像效果与常规 2D-SL0算法相当,但明显好于传统的R-D算法和ESPRIT算法。关于上述四种算法采用实测数据进行ISAR成像的计算时间,情况与仿真数据类似,此处不再列出。
4 结束语
本文提出的2D T-SL0算法是一种压缩感知类参数重构快速算法,可用于ISAR成像。该算法采用迭代效率指标来评估内循环的有效性,以此剔除大量无效内循环迭代,在不影响ISAR成像效果的前提下,大幅减小运算量。本文采用仿真数据和实测数据,对比了2D T-SL0算法、常规2D-SL0算法、传统的R-D算法和ESPRIT算法的计算时间和ISAR成像效果。相较于常规2D-SL0算法,2D T-SL0算法具有更短的ISAR成像计算时间。在ISAR成像效果方面,2D T-SL0算法和常规2D-SL0算法相当,但明显优于传统的R-D算法和ESPRIT算法。

