一类具有恐惧效应的时滞广义HollingⅢ型捕食者-食饵模型的动力学分析

王檄豪, 韦煜明

( 广西师范大学 数学与统计学院, 广西 桂林 541006 )

0 引言

由于恐惧效应会改变食饵种群的行为方式、生理特征以及种群密度等[1],因此近年来一些学者对其进行了研究.例如:2016年,Wang等[2]研究了恐惧效应对确定性捕食者-食饵模型的影响;同年,李梁晨等[3]提出了一类具有时滞HollingⅡ型功能反应的捕食者-食饵模型,并研究了该模型共存平衡点的全局稳定性及其Hopf分支的存在性;2016年,秦爽[4]研究了一类具有广义HollingⅢ型功能性反应的确定性模型的动力学行为;2022年,Shao[5]研究了一类在确定环境和随机环境中带有恐惧效应和时滞的捕食者-食饵模型,并探讨了确定性模型中平衡点的存在性和稳定性以及随机模型中全局正解的存在性;2022年,刘英姿等[6]研究了一类具有恐惧效应的Leslie-Gower型功能反应的捕食者-食饵模型,并讨论了恐惧效应对食饵和捕食者种群密度的影响.基于上述研究,本文基于文献[5]中的捕食者-食饵模型,采用广义HollingⅢ型功能反应函数建立了如下确定性模型:

(1)

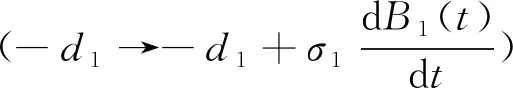
(2)

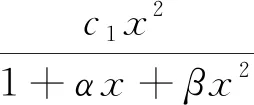
1 确定性模型

下面分别讨论模型(1)平衡点的存在性和局部稳定性,以及其在共存平衡点处发生Hopf分支的条件.

1.1 模型(1)平衡点的存在性

根据模型(1)可得如下方程组:

(3)

(4)

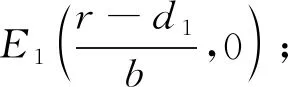
a0x7+a1x6+a2x5+a3x4+a4x3+a5x2+a6x+a7= 0.

(5)

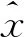
1.2 平衡点处的稳定性分析

本文通过判断特征值的符号来分析模型(1)平衡点的局部稳定性.模型(1)的特征方程[8]为:

det(J0+e-λτJ1-λI)= 0.

(6)

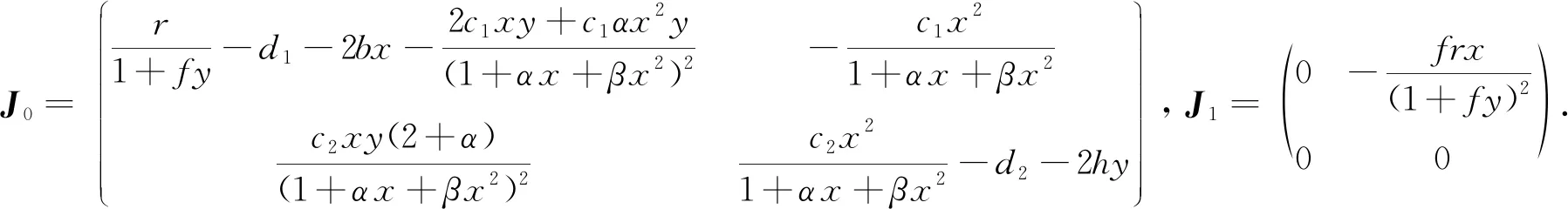
下面分2种情况讨论时滞对模型(1)平衡点处动力学行为的影响.

情形1 无时滞模型的动力学行为.

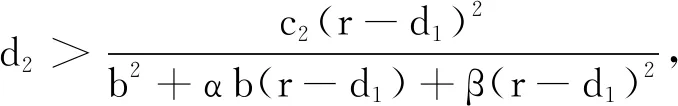
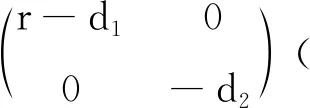
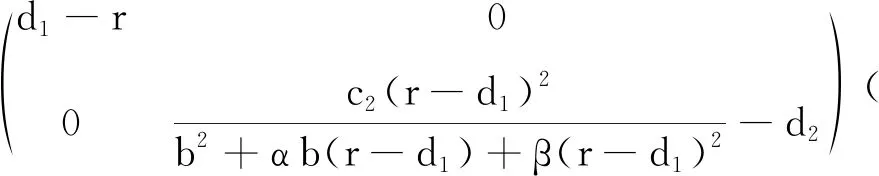
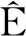
(7)

情形2 带有时滞模型的动力学行为.

λ2+R1λ+R2+S1e-λτ= 0.

(8)

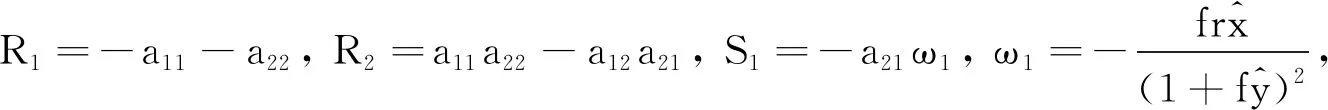
(9)

2p1p2+R1p2-S1e-p1τsin(p2τ)= 0.

(10)

为确定式(8)是否有纯虚根,再令p1= 0.由此式(9)和式(10)可变为:

(11)

S1sin(p2τ)=R1p2.

(12)

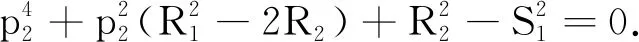
(13)

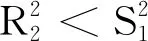
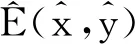
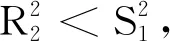
对式(9)和式(10)关于τ进行微分后,再将p1= 0和τ=τ*代入式(9)和式(10)中可得:

(14)

(15)

2 随机模型

2.1 正解的存在唯一性

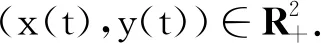
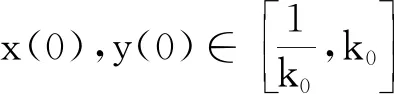
P(τk≤T)≥ε,∀k≥k1.

(16)

(17)

其中:

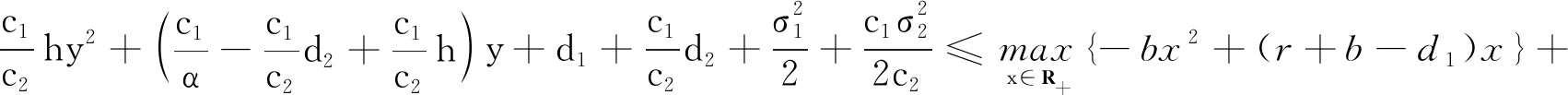
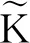
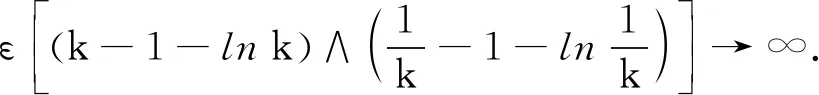
2.2 解的有界性

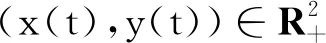
证明由模型(2)的第1个方程可知:

x(r-d1-bx)dt+σ1xdB1(t).

根据上式可构造方程dp(t)=p(r-d1-bp)dt+σ1pdB1(t),由此再由文献[12]和微分方程随机比较定理[13]可知x(t)有上界.

由模型(2)的第2个方程可知:

(19)

为了证明y的有界性,本文根据式(19)构造如下辅助模型(20):

(20)

由式(20)的第1个方程可得:

(21)

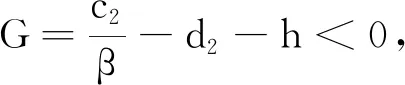
(22)

根据式(22)可构造如下辅助模型:

(23)

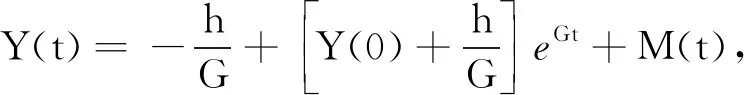
2.3 平均持久性和灭绝性

为了便于下文表述,首先引入以下记号:

引理1[16]假设M(t)∈C([0,+∞],R+),则:

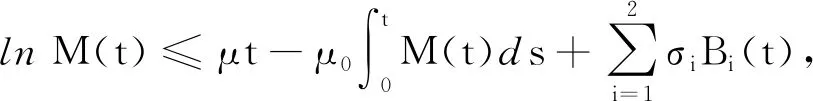
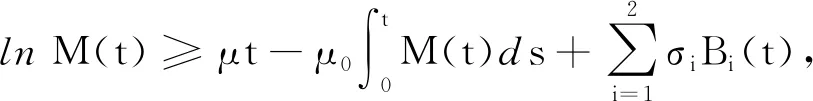
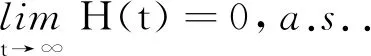
(24)

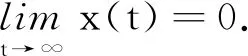
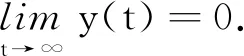
证明对模型(2)的第2个方程应用It公式可得:

(25)

对式(25)两边进行积分可得:

(26)

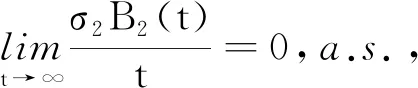
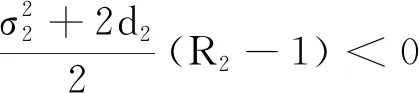
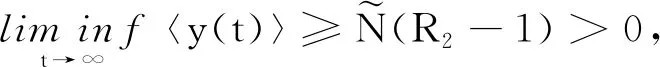
证明对模型(2)和模型(24)的第1个方程分别应用It公式后再对其两边同时进行积分可得:

(27)

(28)

对式(28)两边进行积分后再将式(27)代入其中可得:

3 数值模拟

3.1 恐惧效应对模型(1)平衡状态的影响

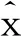
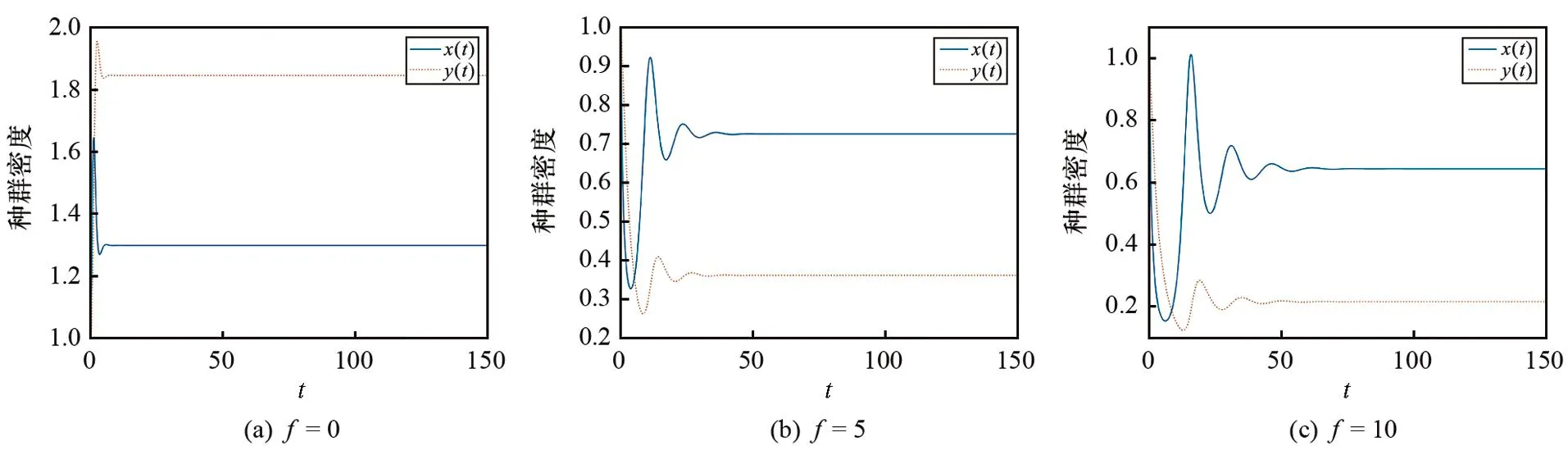
图1 不同恐惧参数f对模型(1)平衡状态影响的仿真图

3.2 时滞对模型(1)平衡状态的影响

本文参考文献[5],选取3个时滞参数τ(1、5和10)来分析时滞对模型(1)的影响(固定f= 1,其他各参数取值与3.1中相同).图2为τ分别取1、5和10时其对模型(1)平衡状态的影响的仿真图.由图2可以看出,不同时滞的取值不会影响模型(1)的种群密度和平衡点的稳定性.

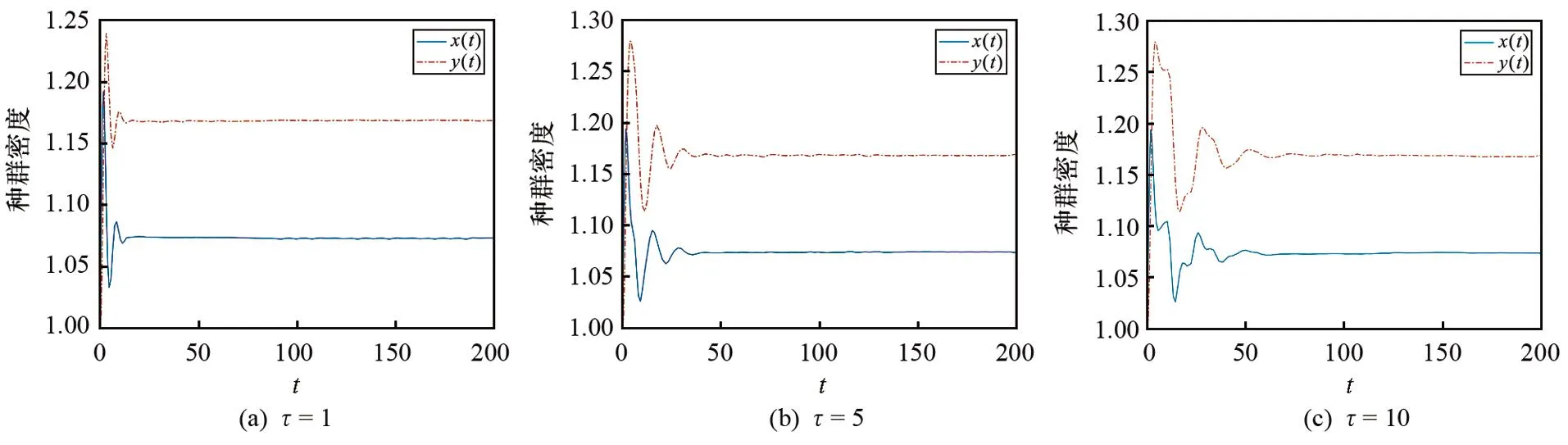
图2 不同时滞参数τ对模型(1)平衡状态影响的仿真图

3.3 随机因素对模型(2)平衡状态的影响

本文利用Milstein方法[19]研究随机因素对模型(2)平衡状态的影响,参数取值参考文献[20]选取:r= 2.2,c1= 0.6,f= 1,τ= 0,d1= 0.5,b= 0.08,α= 0.01,β= 0.01,c2= 0.1,d2= 1,h= 0.3.

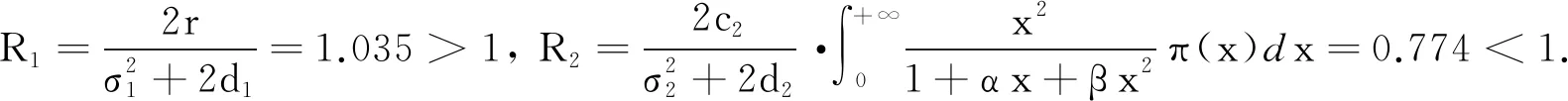
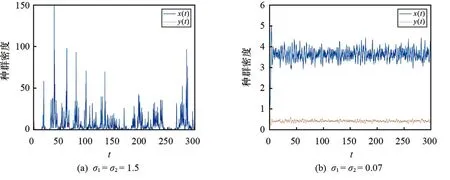
图3 不同随机因素对捕食者和食饵种群密度影响的仿真图

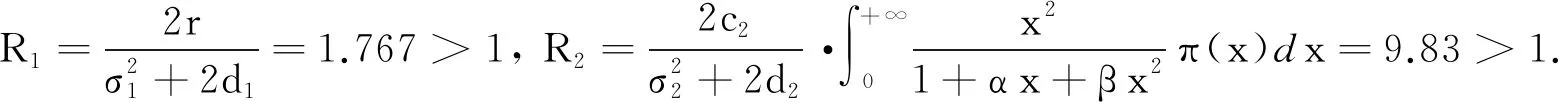
4 结论

本文对确定性模型(1)和随机模型(2)的动力学行为进行研究表明:恐惧效应不会对模型(1)的稳定性产生影响,但会改变食饵和捕食者的种群密度,表现为较高的恐惧效应会降低食饵和捕食者的种群密度;时滞不会对模型(1)的稳定性和种群密度产生明显影响;随机因素对模型(2)的稳定性和种群密度都会产生影响,表现为较大的噪声会降低食饵和捕食者的种群密度.本文研究结果可为调控种群密度和维持种群间的平衡提供良好参考.在今后的研究中,我们将对模型(2)是否存在平稳分布和具有遍历性进行探讨.