基于S 型曲线误差补偿模型优化蠕动泵微量灌装精度的研究

张冠豪，于源华

（长春理工大学 生命科学技术学院，长春 130022）

蠕动泵的微升级灌装常用于体外诊断（In Vitro Diagnosis，IVD）、生物制剂等行业的小剂量自动化灌装生产线中，其精度直接决定了检测试剂及疫苗的分装精度［1-2］。提升蠕动泵微升级别灌装精度将有效提高试剂质量，并避免浪费昂贵试剂。

尽管国内企业正在积极进行自主研发，以跟上国外微升级灌装技术的成熟水平，但是目前国内的灌装设备在灌装精度方面仍然无法达到国外主流产品的标准。此外，相对于国外，国内的研究在采用控制算法软件来提升灌装精度方面还相对较少。

袁佳等人［3］研究了一种基于自适应模糊PID控制算法的蠕动泵输出装置，结合模糊PID 算法将测量值与目标值不断分析比较，以实现减小灌装误差的目的。尽管PID 控制具有一定的控制稳定性，但其调整过程较长，而且不具备整体优化能力，因此，在灌装生产线等需要高效控制的应用场景中，PID 控制方法并不是一个理想的选择。

郑诚等人［4］采用校正宽度理论将毫升级灌装相对误差控制在1% 范围内。肖亚男等人［5］探讨了一种基于蠕动泵的非接触式微量灌装方法，可在确定加样量的前提下，将重复性CV 值控制在2.071% 范围内。以上研究方法尽管可以减小蠕动泵灌装的误差，但均在固定灌装量前提下，通过寻找最佳电机转速实现降低误差。由于蠕动泵在实际灌装过程中的动态特性是时变性且非线性的［6-8］，因此使用上述控制方法进行调节时，其调节性能会受到影响，并且对参数选择具有较大的依赖性。

为此，针对蠕动泵微升级别灌装精度较低且具有非线性时变性的问题，本文通过对蠕动泵的液体驱动原理和步进电机的驱动频率进行分析，构建电机驱动频率与目标灌装量的关系模型，并提出了一种基于S 型加减速曲线的误差补偿模型，可以更精确地控制脉冲频率，达到克服时变性、提高灌装精度的目的。 目前该方法已经成功地应用在了一些对象上，如郑国梁等人［9］提出了一种基于抛物线加减速曲线的误差补偿模型，该模型表现出了较高的灌装效率和精度。本文采用基于S 型加减速误差补偿模型对驱动频率进行优化，并利用建立的模型进行实验验证，通过对自制搭建的蠕动泵灌装装置进行灌装精度实验，并比较无误差补偿的梯形加减速、抛物线加减速的电机驱动频率控制方法，对实验结果进行分析比较，验证所提方法的可行性和稳定性。

1 蠕动泵的液体驱动原理

蠕动泵由驱动器、泵头和软管三部分组成。在蠕动泵正常工作时，它能够通过驱动器带动转子循环挤压软管的方式实现连续性液体驱动，如图1 所示。当转子从A向B方向旋转时，转子将持续对软管进行交替挤压和释放，从而驱动液体不断流动。这种特殊的挤压方式不仅能够确保液体连续、平稳地流动，还能够有效避免其他泵类可能会出现的渗漏或污染等问题。 因此，蠕动泵在工业、医疗、生物科技等领域中得到了广泛的应用［10-11］。

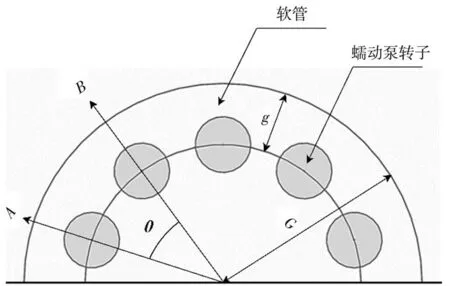
图1 蠕动泵的液体驱动原理

通过对蠕动泵转子的角位移计算，即可得到灌装液体的体积，可用式（1）近似描述：

式中，G为软管外壁至蠕动泵中心的距离；g为软管的直径；μ为液体的粘度系数；θ为步进电机旋转角度。

另外，式（1）也可简化为：

因此，当A为比例常数时，灌装液体的体积ν与步进电机旋转角度θ成正比关系。

2 步进电机驱动频率与灌装量的关系模型

2.1 基于梯形加减速曲线的关系模型

在以梯形加减速算法作为步进电机驱动方式时，如图2 所示，整个运动过程包括3 个阶段：匀加速（0～T1）、匀速（T1～T2）、匀减速（T2～T3）。加速阶段是指经过T1时间运行n1步后达到最大运行频率fmax，即蠕动泵转子由静止状态通过匀加速达到匀速；匀速阶段是指将蠕动泵转子稳定在最大转速，从而实现软管内液体以最大流速灌装；减速阶段是指将蠕动泵转子通过匀减速至静止状态。

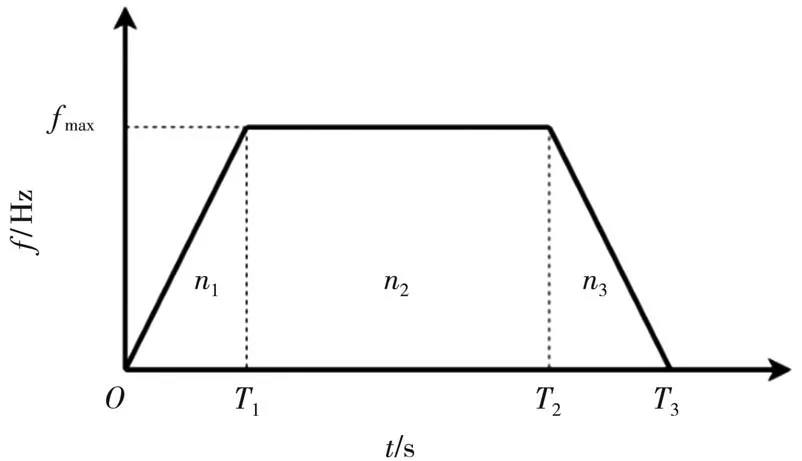
图2 梯形加减速频率曲线

梯形加减速驱动频率模型描述如下：

通过对步进电机频率分析可得到步进电机的角位移为：

式中，λ为最小步进角；a为给定的加速度。将公式（2）与公式（4）结合可得驱动频率与灌装量的关系模型：

2.2 基于抛物线加减速曲线的关系模型

在以抛物线加减速算法作为步进电机驱动方式时，如图3 所示，整个运动过程可以分为加速（0～T1）、匀速（T1～T2）、减速（T2～T3）三个阶段。与梯形加减速算法相比，该方法的启停过程较为平缓。

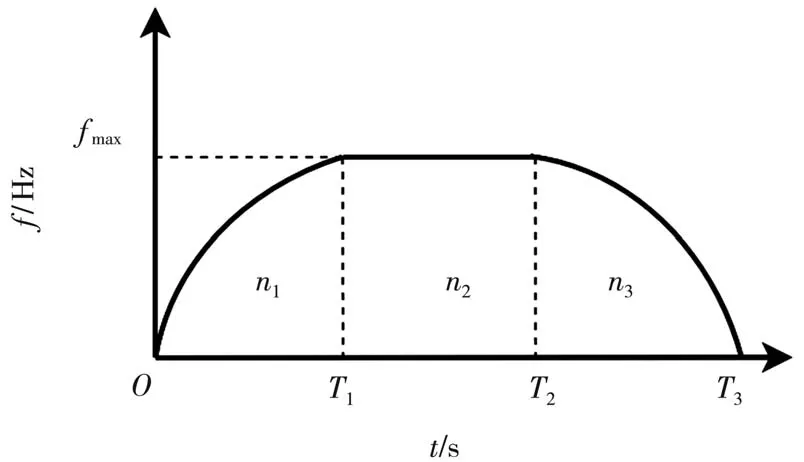
图3 抛物线加减速频率曲线

抛物线加减速驱动频率模型［12］描述如下：

式中，U为比例系数；n为常数；T为给定相同脉冲频率时的时间间隔；T1、T2、T3分别表示蠕动泵转子加速、匀速、减速的截止时刻，T3=T1+T2。通过对步进电机频率f(t) 积分可得到步进电机的角位移［13］：

式中，λ为最小步进角。将公式（2）与公式（7）结合可得驱动频率与灌装量的关系模型：

通过使用梯形加减速算法和抛物线加减速算法对目标液体进行灌装时发现，当电机在加速度突变时（T1、T2时刻），会导致软管内的液体出现脉动现象，并产生气泡，从而对灌装精度造成影响［14］。

2.3 基于S 型加减速曲线的关系模型

在以S 型加减速算法作为步进电机驱动方式时，如图4 所示，整个过程分为了7 个阶段［15］：加加速（0～T1）、匀加速（T1～T2）、减加速（T2～T3）、匀速（T3～T4）、加减速（T4～T5）、匀减速（T5～T6）和减减速阶段（T6～T7）。

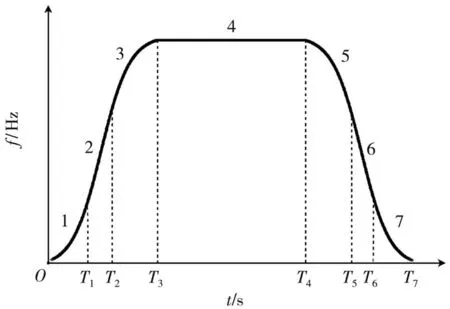
图4 7 段S 型加减速频率曲线

S 型加减速驱动频率模型［16-17］描述如下：

式中，tα表示各速度阶段的截止时刻（α=1，2…，7）；τα表示各速度阶段起始点时刻（τα=tα-tα- 1，α=1，2…，7）。

步进电机的角位移为：

式中，λ为最小步进角。将公式（2）与公式（10）结合可得驱动频率与灌装量的关系模型为：

2.4 基于S 型加减速曲线的误差补偿模型

通过对式（8）与图4 进行分析可知，在0～T3时间序列内，驱动频率的差值由大到小变化并不连续，本文假设由于这种驱动频率的不连续导致了软管内的液体出现脉动，产生气泡的现象，从而对灌装精度造成影响，且在0～T3时间序列内其影响程度与驱动频率差值的平方成正相关关系；在T4～T7时间序列内正好相反。 在T3～T4时间序列内驱动频率无差值，因此无脉动、产生气泡的现象，但由于存在系统误差，步进电机角位移的重复定位精度会随着T3～T4持续的时间成反比关系。

综合上述问题进行分析，建立误差补偿模型［18］：

式中，β为由于出现脉动、气泡的现象造成的误差补偿参数；ξ为T3～T4步进电机角位移的误差补偿参数。将公式（11）与公式（12）结合可得：

在实际灌装应用时根据灌装量选择合适的参数值对公式（13）进行描述，并对公式（9）进行相应的脉冲频率控制，实现基于S 型加减速曲线的误差补偿灌装。

3 仿真与实验验证

3.1 仿真验证

利用Matlab2020 对梯形、抛物线和有补偿的S 型加减速算法分别进行仿真，速度曲线如图5所示；驱动频率对应图6 所示的脉宽调制（Pulse Width Modulation，PWM）脉冲信号，其作用是驱动步进电机驱动器工作。结合细分驱动技术［19-20］可知，细分电流每变化一次，步进电机旋转一步。在一定的时间范围内给定相同驱动频率，由于脉冲数是已知量，则步进电机的旋转角度即可确定，通过对该时间范围内的脉冲数进行累加，即可得到步进电机的旋转角位移。

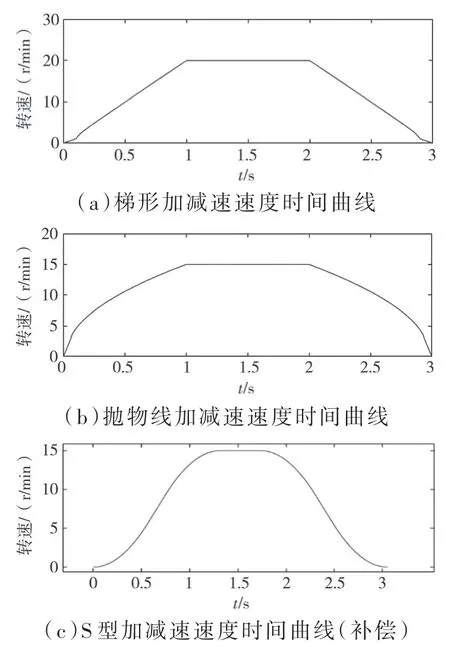
图5 三种类型加减速算法速度时间曲线

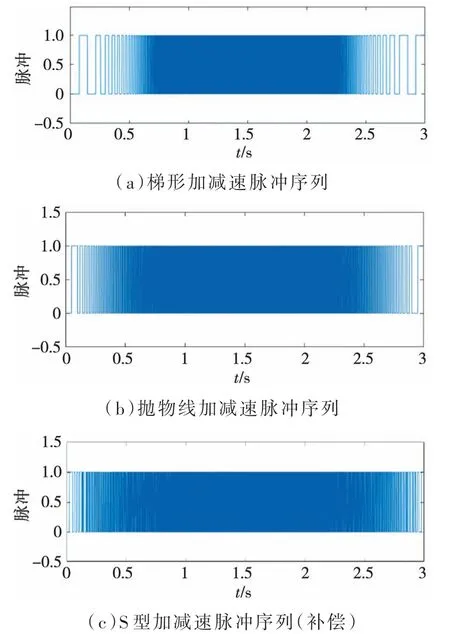
图6 三种加减速算法脉冲序列

从图5 的仿真结果可以看出，使用误差补偿模型的S 型加减速曲线在步进电机状态切换时具有更平缓的过渡。另外，通过对图6 的脉冲序列仿真结果的分析发现，具有补偿的S 型加减速算法在0～1 s 的加速状态和2～3 s 的减速状态下，脉冲数更为密集。综上所述，基于S 型加减速曲线的误差补偿模型可以更精确地控制脉冲频率，从而提高蠕动泵微升级的灌装精度。

3.2 实验验证

为了进一步验证所提方法的正确性，搭建如图7 所示的蠕动泵灌装装置。选用了STM32F03 VET6 作为系统主控芯片，STM32 是ST 公司（意法半导体）基于Cortex-M3 内核设计的一款嵌入式微控制器，选用57 步进电机和雷赛智能生产的DM542 步进电机驱动器进行控制。蠕动泵转子数为6转子；软管管号为1×1（内径1 mm，壁厚1 mm）；步进电机驱动细分数n=32；转速设置为100 r/min。

图7 蠕动泵灌装装置

分别使用梯形、抛物线和有补偿的S 型加减速曲线的驱动频率控制方式对纯化水进行灌装，使用无补偿的梯形、抛物线灌装方式时β=0，ξ=0；40 µL 时补偿β值=1.018，ξ=1.007；100 µL时补偿值β=1.009，ξ=1.005；200 µL 时补偿值β=1.008，ξ=1.004。并测出当目标灌装量为40 µL，100 µL，200 µL 时的实际灌装量。

3.3 实验方法与步骤

实验设备有蠕动泵灌装装置、电子天平（BSA 124S）、EP 管、纯化水，如图8 所示。

图8 实验设备

实验步骤：

（1）天平调平、去皮。

（2）取一空EP 管置于托盘，待示数稳定后记录其质量。

（3）取出EP 管，使用蠕动泵灌装装置，根据实验要求的目标灌装量进行灌装。

（4）将灌装完成的EP 管放回托盘，待示数稳定后记录其质量。

（5）切换灌装量、加减速算法后重复上述操作。

3.4 实验结果与分析

灌装精度实验对三种加减速算法分别灌装40 µL，100 µL，200 µL，每种算法各进行了十次灌装实验，通过计算灌装前后两次称重所得质量数值的差值，即可得到灌装量，灌装测量结果如图9 所示。三种加减速算法灌装的测试结果如表1所示。

表1 三种加减速算法灌装的测试结果

对图9 与表1 的灌装结果进行分析可知，使用具有补偿的S 型加减速算法对蠕动泵转子进行驱动，CV 值与极差均较梯形加减速、抛物线加减速算法低，实验结果验证了在蠕动泵微量灌装时使用基于S 型加减速曲线的误差补偿模型可以提高灌装的精度与稳定性。

4 结论

对蠕动泵的液体驱动原理与电机驱动频率进行分析，建立了灌装量与驱动频率的关系模型，并针对灌装中误差，提出了一种基于S 型加减速曲线的误差补偿模型。

将所提方法与梯形加减速曲线、抛物线加减速曲线的控制方式进行仿真与实验验证，仿真结果表明该方法在蠕动泵微升级灌装时，驱动频率的稳定性与精确性均优于梯形加减速曲线、抛物线加减速曲线的驱动频率控制方式，实验结果验证了所提方法具备较高的精度与可行性。