甘蔗渣发酵制取乙醇温度模糊控制研究

王雨萌，苏拾，冯进良，马韵琪

（长春理工大学 光电工程学院，长春 130022）

工业中生产乙醇的方法可以分为发酵法和合成法。 发酵法就是日常生活中所熟悉的酿酒，即用各种含有糖分、淀粉或是纤维素的农副产品以及野生植物等作为原材料进行发酵过程［1］。 整个生产过程包括原料蒸煮、糖化剂制备、水解、酵母制备、发酵及最后的蒸馏等工序［2］。 通常而言制备一吨乙醇可以消耗3 吨多的粮食，所以对农副产品丰富的国家来说，使用发酵法制备乙醇非常便捷。而合成法则是用乙烯作为原材料，通过化学合成的手段进行乙醇的生产。 之后随着石油化工产业迅速发展，越来越多的乙醇通过合成法进行化学合成制备，但这种工业合成的乙醇中含有异构高碳醇［3］，对人体有麻痹作用，不宜用在食品医疗等和人们生活息息相关的方面。 所以，即便在石油化工高度发达的国家，发酵法制备乙醇仍有一席之地。

通过多年的研究与探索，国内外的科研人员在发酵控制技术方面有了很大的进展。 Maeda等人［4］在发酵制取乙醇实验过程中，利用补料策略与同步糖化发酵技术相结合，提高了最终的乙醇浓度。 Nasimi 等人［5］将粒子群优化算法与反向传播算法相结合，形成一种新的进行人工网络学习训练的算法，将优化后的算法应用于酵母发酵生物反应器的建模中，验证了新算法的优越性。Moha 等人［6］则对乙醇发酵制备过程的温度控制提出了一种基于分数阶模糊PD/PI（FOFPD/FOFPI）的级联控制策略，使用FOFPI 控制乙醇浓度，FOFPD 控制温度，较其他控制器相比控制精度获得了提高。王秋平等人［7］设计了一种基于蚁群算法、BP 神经网络以及PID 控制的协同控制算法，对火电厂主汽温控制进行了优化，增加了系统的鲁棒性和稳定性。 王健林等人［8］通过对酵母发酵产生谷胱甘肽的过程分析，用乙醇浓度作为主要控制变量，构建了模糊控制器实现对发酵过程的流加速率优化。通常为了稳定生产操作，国内甘蔗渣发酵制备乙醇的过程大都采用常规的控制策略，但常规控制策略在面对像发酵这样复杂的过程时，往往显得不足，难以达到高质量的控制要求。 本文在常规PID 控制的基础上添加了模糊控制，这种控制方式基于操作知识经验，能满足复杂控制对象的控制要求，且能适应对象的不确定性，不需要对被控对象进行高层级的理论描述，具有良好的适应性。

1 温度控制方法分析

在甘蔗渣发酵控制过程中，数字PID 控制算法可靠性较高且使用简单，所以通常使用数字PID 控制算法进行传统的温度控制，但由于温度变化具有滞后性大以及非线性和时变性的特点，有可能会导致出现参数整定不良、超调量大等现象［9］，故选择加入模糊控制。

模糊控制有效地避开了被控对象的复杂数学模型，以操作人员的经验以及相关专家的知识库存作为制定规则实现复杂系统控制的基础，并且它具有良好的鲁棒性，同时被控对象参数存在滞后性的变化不敏感，因此可以有效弥补单纯的数字PID 控制的不足。

模糊控制的基础是模糊集合理论的模糊逻辑，是用模糊逻辑对人的思维进行模仿，对那些具有非线性和时变性特点的复杂系统进行控制［10］。 其中模糊控制器是整个控制系统的核心，主要包括模糊化接口、知识库、模糊推理机和解模糊接口，其基本原理结构如图1 所示。

图1 模糊控制结构

在设计模糊控制器时，要根据被控对象的具体情况和系统的性能指标要求进行控制器的结构选型。模糊控制器的控制规则通常是根据专家知识或操作经验得出的，而实际操作时只能观察到被控对象的输出变量及其变化情况［11］，因此，在模糊控制器中，选取误差和误差的变化率作为输入变量，把系统控制量作为输出变量，这样就确定了模糊控制器的结构。

对于甘蔗渣发酵温度变化的特征，选择模糊控制和PID 控制相结合，即Fuzzy-PID 控制系统对甘蔗渣发酵的温度进行更加精确的调节，其控制思想为：整体发酵过程中，若温度的偏差值e较大的时候，采用模糊控制（Fuzzy）来加快系统的响应速度，以便得到更加优越的瞬态性能；偏差e较小时，整体的温度控制系统自动转变为数字PID 控制，达到去除静态误差的效果，可以提高整体的控制精度。 具体的控制方法由PLC（Programmable Logic Controller）程序根据设定的偏差值自动实现，可以获得优秀的控制效果，且整体系统更加稳定［12］。这种发酵的温度模糊PID（Fuzzy-PID）复合控制系统原理如图2 所示。

图2 温度模糊PID（Fuzzy-PID）系统原理

在该Fuzzy-PID 控制系统中。图中k为控制开关。 中部为该控制系统的关键，包括两种控制方式的切换及各自控制算法基于PLC 的实现。此控制系统中，不论PID 控制器还是模糊控制器均由PLC 程序控制切换，以增加系统可靠性，产生优越的控制结果［13］。

2 温度模糊控制器设计

模糊控制器精确量的模糊化处理：

设偏差基本论域为[ -emax,emax]，差的模糊集合论域为[ -n, -n- 1,…n- 1,n]，其中emax是精确量最大值，通过量化因子ke进行论域变化。量化因子确定则系统的任何一个偏差e都可以量化为论域中的某一个元素［14］。

在温度模糊控制器中，温度的偏差论域取（-5，5），偏差变化率基本论域为（-0.2，0.2），取n=6，E的论域取X1={-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6} 。

EC的论域取X2={-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6} ，可得ke= 0.4，kΔe= 7.5。

对温度偏差变量选用PB、PM、PS、PO、NO、NS、NM、NB 语言变量值（E）分档，偏差变化率选用NB、NM、NS、O、PS、PM、PB 语言变量值（EC）分档，隶属函数为正态函数［15］，其曲线如图3 所示：

图3 正态分布隶属函数曲线

根据甘蔗渣发酵生产乙醇温度变化的相关特性和操作人员的生产经验可以得到语言变量E赋值表，如表1（其中语言值为列元素，E为行元素）所示，语言变量EC赋值表如表2（其中语言值为列元素，EC为行元素）所示。

表1 语言变量E 赋值表

表2 语言变量EC 赋值表

U的论域取U= {-7，-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6，7} ，选择NB、NM、NS、O、PS、PM、PB 作为语言变量值，语言变量表赋值如表3（其中语言值为列元素，U为行元素）所示。

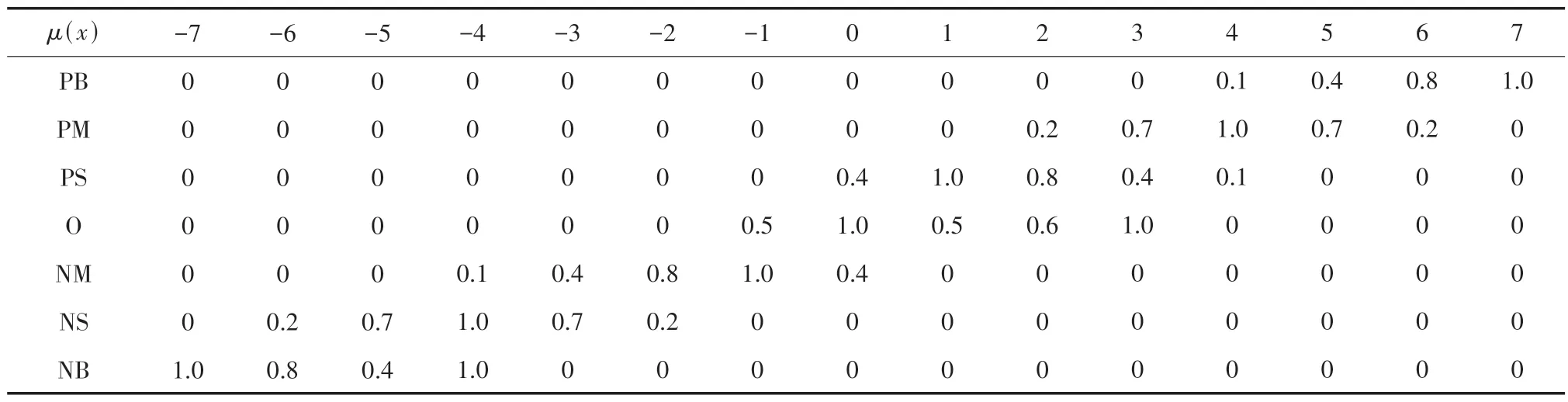
表3 语言变量U 赋值表

根据甘蔗渣发酵人工控制的经验，总结出56条控制规则，这些规则均由模糊控制语句构成，对于双输入（E和EC）以及单输出（U）的模糊控制器［16］，通常写为If E and EC then U，具体到发酵温度模糊控制中则可写为If E=PB and EC=PB then U=PB，此模糊语句代表发酵过程操作人员的其中一条经验，如果发酵温度过低且不断下降，此时加热盘打开最大，同时冷却水阀门保持关闭，使得水温迅速上升。 这些控制规则制成温度模糊控制规则表，如表4 所示（其中E为列元素，EC为行元素）。

表4 模糊控制规则表

表4 中的每一条规则都决定一个模糊关系，其中：

温度模糊控制查询表：

由上述可得总的模糊关系R，利用合成规则公式进行计算，具体公式为：

通过E和EC的所有元素在对应的论域上的模糊集Ei和ECj，可以求出语言变量U的模糊子集Uij，采用最大隶属法对该模糊集合进行模糊判决［17］，得到模糊控制查询表（其中E为列元素，EC为行元素）如表5 所示。

表5 温度模糊控制查询表

模糊控制器输出量U的转换：

模糊控制查询表中的U值不能直接用来控制阀门打开使水温加热，要将U对应变为电流信号μ才能对阀门进行控制，其中电流信号u的范围为4～20 mA［18］。

模糊控制器输出量U的论域为（-7，7），用比例因子变换可得对应输出基本论域为（-8，8），转换为电流信号可得控制加热盘开启以及冷却水阀动作的实际电流值。

3 模糊PID 控制仿真验证

使用甘蔗渣发酵罐基于数据和热交换方程得到数学模型：其中，X(t) 是状态变量；u(t) 是输入变量；Y是输出变量；e(t) 表示干扰。通过过程识别和模型验证获得矩阵A、B、C、D如下：

通过引入单位阶跃变化将状态空间模型转换为传递函数模型［19］：

经过简化，将分子和分母的常数项忽略，并且将等式的极点为零时取消，最终得到：

将过程模型简化为具有时间延迟的二阶积分过程，方程的逆响应项可近似为延时项［20］，即：

最终近似传递函数模型可得到：

用Matlab 进行仿真验证系统的准确性，并将模糊PID 与常规PID 控制器相比较，具体的仿真结果如图4 所示。

图4 Fuzzy-PID 与PID 仿真结果

由图4 可得Fuzzy-PID 与PID 性能指标对比结果如表6 所示。

表6 Fuzzy-PID 与PID 性能指标对比结果

对比两种结果，采用Fuzzy-PID 控制的系统具有响应快与精确控制罐温的优点，控制结果比普通经验控制更加好，它的上升时间和调节时间对比PID 控制来说均缩短，并且稳态误差也小，提高了发酵过程的动态性能和静态性能指标［21］。

4 PLC 整体控制发酵实验结果

在控制过程中，控制系统使用STEP 7-Micro/WIN 软件进行程序编辑，用脉宽调制输出控制阀门打开、水温加热或降低，从而进行温度控制。其部分程序如图5 所示，其中，图5（a）为偏差值e量化处理程序，图5（b）为模糊控制查询表在step7 中的实现。 偏差E的实际值存放在VD20中，经量化处理后的E值存放在VD24 中，同理可得到量化处理后的EC值，ROUND 指令为取整操作，即取最接近的整数值。

图5 部分PLC 程序

实验过程中的实验设备图如图6 所示，其中罐体实物图如图6（a）所示，控制面板如图6（b）所示。

图6 实验设备

总体系统采用Fuzzy-PID 控制对甘蔗渣发酵系统进行控制，经反复调试后取得了较好的控制效果。

在实际生产发酵过程中，将甘蔗渣发酵制取乙醇罐温设定值从36 改为35.5，每5 s 记录一次数据，表7 为复合模糊PID（Fuzzy-PID）的一组数据，表8 为常规PID 控制的一组数据。

表7 Fuzzy-PID 控制温度数据

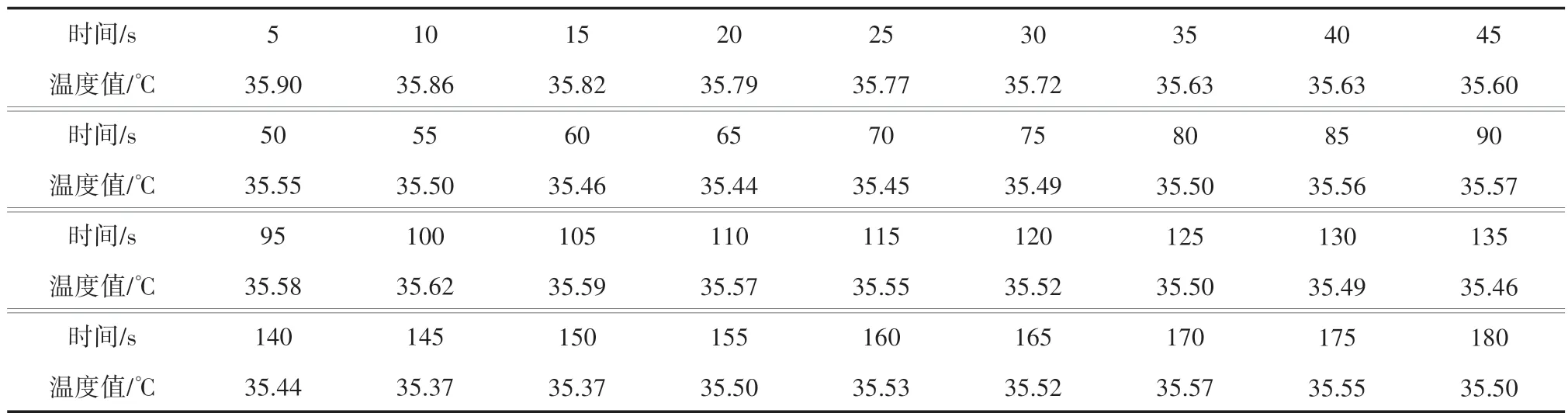
表8 常规PID 控制温度数据表

将上述表格绘制折线图，如图7 所示，用折线图直观进行对比可得Fuzzy-PID 的超调量比PID 控制降低35%，调节时间缩短20%，Fuzzy-PID 控制的动态性能和静态性能全面改善，表现出良好的鲁棒性［22-24］。

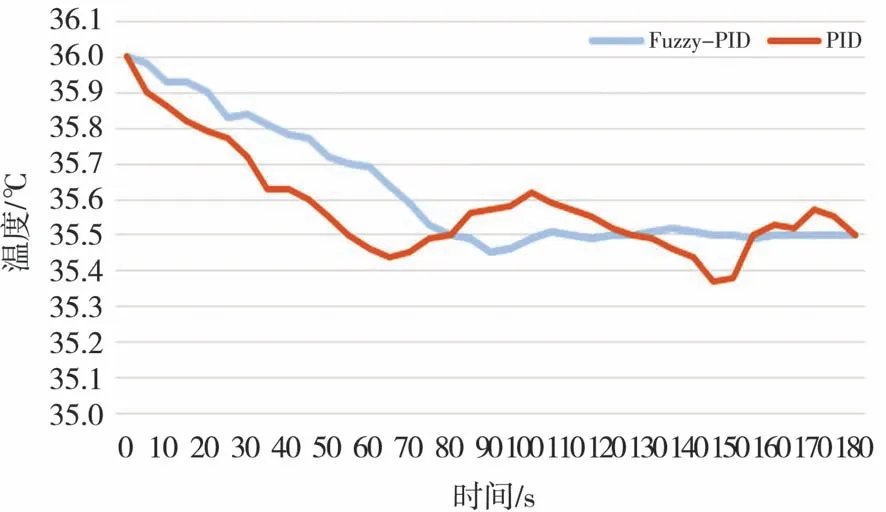
图7 Fuzzy-PID 与PID 折线对比结果

表9 为调试完成后的另一组温度响应数据：在发酵温度稳定（设定值与实际值均为35.4 ℃）的前提下，将温度设定值修改为35.5 ℃。 根据表9 可制成折线图，如图8 所示，大约35 s 后发酵温度稳定至35.5 ℃左右，控制效果符合工艺设计要求。

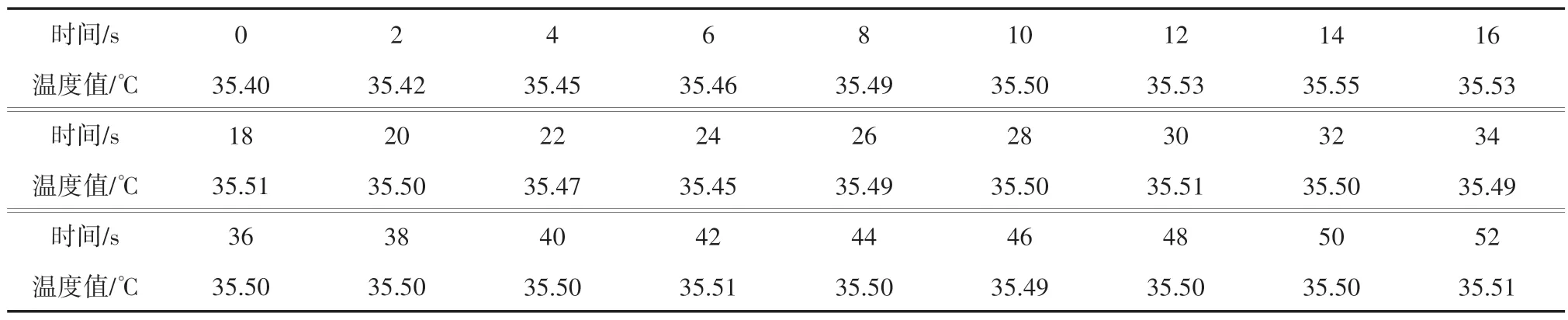
表9 发酵温度控制调试数据

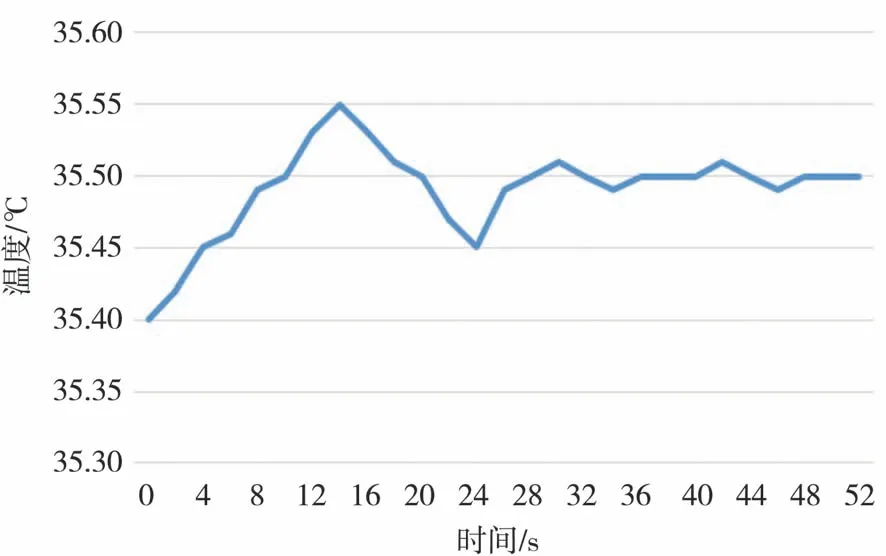
图8 发酵温度控制调试数据

5 结论

为了解决PLC 控制的甘蔗渣发酵制取乙醇过程中温度控制超调大、实时性差、响应慢的问题。 本文使用模糊控制PID（Fuzzy-PID）控制策略。通过构建数学模型并利用Matlab 进行仿真，与传统PID 控制进行了比较，证明了该算法具有实时性强、过冲小、鲁棒性好等优点，大大提高了系统性能，可以满足在发酵制取乙醇过程中的温度控制需求。同时使用STEP 7-Micro/WIN 软件进行PLC 系统的编程，系统采用数字控制算法对发酵温度进行控制，在同一条件下，Fuzzy-PID的超调量比PID 控制降低35%，调节时间缩短20%，Fuzzy-PID 控制的动态性能和静态性能全面改善，表现出良好的鲁棒性。经反复调试后，在发酵温度稳定设定值与实际值均为35.4 ℃的前提下，将温度设定值修改为35.5 ℃，大约35 s后发酵温度稳定至35.5 ℃左右，控制效果符合工艺设计要求。