利用数据库技术的近红外消光法颗粒粒度测量

王鸿钦，郑泽希，项华中，李祥鹏

（上海理工大学 上海市介入医疗器械工程研究中心， 上海 200093）

引言

颗粒粒径的测量在环境监测[1]、生物医学[2]、制药、化工[3]等众多领域有着重要的意义。光散射法的先进性促成了其在粒径测量中的广泛使用[4]，而消光法的原理及测量相较于其他光散射法更为简单[5]，对于目前使用较多的粒度在线测定具有较大的应用空间。消光法利用经颗粒散射后的连续透射光谱或离散多波长光谱进行反演运算j 进而求得颗粒粒度与尺寸分布[6-7]。

求颗粒粒径的反演方法一般有两类。一类为独立模式法，即不使用某种函数关系来近似描述颗粒粒径分布，而直接通过求解相关离散方程计算出粒径。另一类为非独立模式反演算法，假设所求的粒径分布符合某个函数规律[8]，然后利用优化算法比较理论计算值和实测值，搜寻出最佳分布。非独立模式法涉及更少的自变量，其运算复杂度较独立模式法更低。国内外对颗粒粒度反演的各种算法进行了诸多探索。孙晓刚等[9]利用全局性的遗传算法同时按照三类分布函数来反演，获取了粒径近似分布规律的同时也避免了搜寻时困于局部极值的情况。赵蓉等[10]通过非线性最小二乘法反演小于10 µm 的粒径，再通过图像法反演超过10 µm 的粒径，达到了测量跨微米混合粒径的目的。Ping 等[11]用主成分分析探究消光数据与波长间关系以筛选出最佳波长，并结合BP 神经网络对粒径分布进行计算，以提高计算收敛的速度和计算结果的稳定性。然而，在采用近红外窄波段光源的消光法粒径测量中，仍较难找到一种粒径反演准确性较好的算法。李祥鹏等[12]采用近红外窄带宽光源，通过人工蜂群算法对透射消光光谱反演粒径，取得一定效果。本文则引入新颖的数据库技术，相较于传统的反演算法，该方法可预先计算及建立仪器测量范围内的含颗粒粒度及尺寸分布的数据库，并利用光谱特征结合数据库高效的管理与查询能力来减小搜寻范围及复杂度，实现较高效率的全局搜寻，同时降低易困于局部极值的风险。

目前的社会生活与大数据的联系愈发紧密[13-14]，数据量的剧增促使数据库技术的兴起与成熟。数据库技术是一种能够对已有的海量数据进行有效存储、管理及分析的技术手段，已在模式（指纹、人脸等）识别等众多领域得到广泛应用[15-17]。本实验采用在医学无创检验如血氧饱和度、血糖等测量中[18-19]使用的近红外窄波段光源。相比消光法颗粒粒度测量中常用的可见光宽波段光源，近红外窄波段的消光光谱法反演难度更大，但本文提出的基于数据库技术的求颗粒粒径的反演算法取得了较为满意的实验结果。因为数据库是预先建立的，在实测时本文方法的反演速度较快，精准度高，且对双峰分布也同样有较高的精度。

1 颗粒粒度的求解方法

1.1 消光法

本文以散射消光的Lambert-Beer 定律为基础。设一平行光束的波长为λ、光强为I0，使它穿过待测区域。待测区域里悬浮在介质中的颗粒会散射光束，则经过待测区后的光强I会被削弱[20]。当介质内悬浮物为多分散粒子群时，出射光强与入射光强的关系表示为[9]

式中：I/I0为反映光强削弱度的消光值；λ、m及D分别为波长、相对折射率及粒子尺寸；Kext为消光系数，利用Mie 理论以及函数关系算得[21]；常量Q=-3LND/2，L为光束穿过待测区时经过的光程，ND为待测区所含颗粒总和；f(D) 为待求的描述不同粒径所占体积频度比例的颗粒尺寸分布函数[9]。式（1）属于Fredholm第一类方程，通常依靠数值积分法求解，经此法离散后得[9]

出射光强I可由式（3）进行变换得[12]

1.2 数据库的构建

数据库存储ID 和相应的分布函数、光谱数据、特征数据这4 部分内容，ID 为标识每条数据的编号。

根据设定的尺寸分布和式（3）或式（4），在MATLAB 中算出对应的由消光值或透射光强构成的光谱曲线，接着算出在光谱曲线上的几个特征值（如斜率、距离、均值等）。连接数据库软件PostgreSQL，将上述尺寸分布及光谱数据、特征数据存入PostgreSQL。PostgreSQL 是目前所有开源数据库中功能最为强大的数据库管理软件，可支持不同语言自行编程如计算欧氏距离等程序。

特征数据用于缩小计算范围，减少计算时间，否则实测光谱数据将不得不与库中海量光谱数据逐一运算比较。光谱具有形状、数据等方面的特征，其中数据方面主要有描述离散度、衡量集中度及表征变化趋势等方面的特征。由于实验所用的近红外波段较窄，每组光谱数值之间差别小，光谱离散性小且光谱间形状差异小，光谱对离散程度及形状方面的特征不敏感，因此本文从数据集中程度和变化趋势两个区分度更显著的方面选取平均值、中位数及斜率作为光谱曲线的特征参数。其中，斜率特征S设定为

式中：Ei是每条光谱数据；λi为各光谱数据对应的波长。特征数据之间一般都存在较大甚至不同数量级的差异，难以用一个确定的阈值找出库中与实测光谱特征最相似的光谱曲线。所以本文采用对特征相似度T进行排名的方法并提取排名靠前的数据。特征相似度T设定为

式中t1和t2分别代表实测的光谱和理论算得的光谱的特征数据。

1.3 数据库的运行

在PostgreSQL 中，输入实测的光谱数据、特征数据。数据库分别按照3 种特征相似度T的升序排名重新排列所有数据，并分别提取在设定的排名指标内的数据集合ax，x∈{1,2,3} 。得到数据集合ax后，提取3 个集合中ID 的交集及ID 后面的数据，得到数据集合b，则b中光谱满足各个特征都与实测光谱特征最相似。若出现ID 交集为空的情况，则逐步倍数扩大排名指标，重新进行上述步骤。最后对b所有数据按照每条光谱数据与实测光谱数据的目标函数值的升序进行重新排列，b中第一条数据的分布参数便是所求的尺寸参数。目标函数为[10]

式中：E1为实测的光谱数据；E2为理论计算的光谱数据；l为波长数量。

由于排序时大量数据无法一次性放进内存，故使用多路归并排序（multipath merge sort, MMS），其将待排序的数据集在磁盘中分为多个体积小于内存的子集合，对每个子集合进行快速排序（quick sort, QS）并将各自最小的数存入内存，对内存的数进行快速排序并将最小的数存入磁盘，接着将此数所在的有序子集合的下一个数替补到内存，继续将内存中最小的数存入磁盘，重复以上步骤直到排完数据集。图1 为排序的流程图。

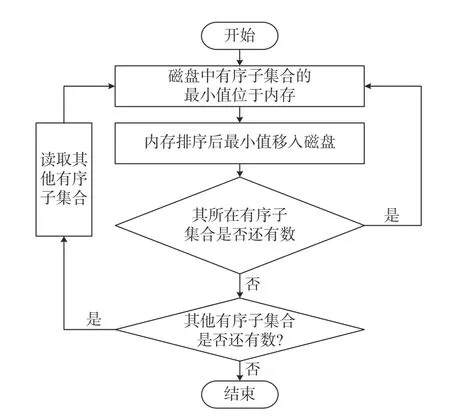
图1 排序的流程图Fig. 1 Flow chart of sorting

2 仿真和实验

2.1 仿真

近红外光源中心波长为 850 nm ，取波段835～865 nm，颗粒相对于水的折射率m为1.591/1.33，粒径范围为0.1～30 µm。由于实际的多数颗粒粒径分布满足Rosin-Rammler 分布[8]，本文使用R-R函数作为f(D) 。其中单峰分布为

双峰分布设为

式中：D和k分别为反映粒径大小和分布宽窄的两个参数；n∈[0,1][10]。用相对均方根误差（relative root mean square error, RRMSE）来评价反演结果，其表达式为

式中：fin(D) 为理论上的分布；fout(D) 为反演得到的分布；R为相对均方根误差。数据库中单峰分布参数区间设定为：∈[1,30] ，k∈[1,15] ，步长均为0.01，库中约400 万条数据。双峰分布的几个参数也作类似设定。排名指标设定为前2.5%。

表1 为单峰分布仿真结果，表2 为双峰分布仿真结果。

表1 单峰分布仿真结果Tab. 1 Simulation results of unimodal distribution

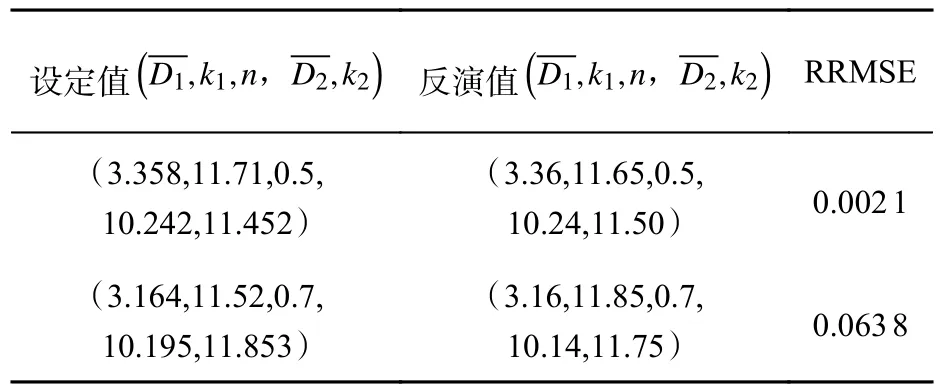
表2 双峰分布仿真结果Tab. 2 Simulation results of bimodal distribution

单峰和双峰分布仿真结果的误差都小于10%，算法的仿真效果较为令人满意。

为研究本方法对噪声的抗干扰性，对上述分布参数的光谱数据多次加入不同大小的随机噪声，以10 次运算结果的平均值作为反演值，表3为仿真结果，图2 为体积频率分布曲线。

表3 加噪后仿真结果Tab. 3 Simulation results after adding noise

图2 仿真结果的体积频率分布曲线Fig. 2 Volume frequency distribution curve of simulation results

单峰和双峰分布仿真结果的误差随着随机噪声的增加而增加，但误差仍在10%内，说明算法对噪声具有一定的抗干扰能力。

2.2 标准颗粒实验

使用编号为GBW120134、GBW120024、GBW120041 的国家标准颗粒进行实验来验证算法的有效性。

三者的D50 粒径标称值为3.44 µm、9.40 µm、14.62 µm，实验的参数条件设置同仿真部分。

进行单峰分布实验时，分别测量3 种颗粒的入射光强和透射光强，按照第1.2 节建立相关数据库，输入实测的光谱数据、特征数据进行运算，表4 为实验结果。从表4 可以看出，反演实测值与D50 标称值的相对误差均在10%以内。

表4 标准颗粒单峰分布实验结果Tab. 4 Experimental results of unimodal distribution of standard particles

进行双峰分布实验时，将D50 粒径分别为3.44 µm、9.40 µm 的颗粒混合于蒸馏水中，后续实验过程同前述单峰测量部分，表5 为实验结果。图3 分别给出了部分实测的单峰及双峰分布颗粒的体积频率分布曲线。从表5 可看出，标准颗粒D50 标称值与实测值的相对误差均在10%内。

表5 标准颗粒双峰分布实验结果Tab. 5 Experimental results of bimodal distribution of standard particles

图3 实验结果的体积频率分布曲线Fig. 3 Volume frequency distribution curve of experimental results

3 结论

本文提出了一种基于数据库技术来实现近红外窄波段反演颗粒尺寸的计算方法。预先建库存放与颗粒尺寸及分布参数相关的光谱数据，并结合光谱特征与数据库高效的管理与查询能力来减少复杂运算、提升运算效率并降低易困于局部极值的风险，做到较准确的全局搜寻。本文对提出的算法进行了数值仿真和标准颗粒的实测，测量准确度均在10%内，取得了满意的结果，从而验证了将数据库技术用于近红外窄波段消光法的颗粒测量是可行的和有效的，也给生物医学中利用近红外光进行体外以及体内的无创血糖检测等提供了一个新的思路。