等宽拉深筋截面参数生成机理与参数化设计

丁顺风，刘 庆，张胜利

（一汽模具（天津）有限公司，天津 301509）

0 引言

拉深筋在大型覆盖件的冲压成形中起着关键作用[1]，最直接表现为控制板料流入量。在外板类覆盖件冲压成形中，一般为胀形成形，拉深筋起着锁料的作用[2]，使板料减薄率和主应变达到所需数量值，以提高外板件的刚度。在内板类覆盖件拉深成形过程中，拉深筋可以控制板料均匀流入，以消除起皱缺陷[3]，汽车典型的零件如后背门内板，其拉深时若为V 形拉深，则中间灯口附近的密封面易起皱，需要通过拉深筋调整流入量，以消除此处起皱。

在汽车生产过程中，提高冲压件的材料利用率将间接推动“双碳目标”的达成。拉深筋重要的作用是控制板料的流入量，通过优化拉深筋的设计，可以提高材料利用率，但是在优化设计过程中需要不断更改拉深筋的参数并进行模拟计算才能实施。目前的三维设计软件尚无完备的拉深筋设计模块，即便有拉深筋设计命令，也不能准确设计低高度的拉深筋，其设计参数固定，不能随拉深筋高度的变化而变化。

为了全参数化设计拉深筋，国内外展开了长期的研究，开发了一些设计系统。种亮等[4]提出了拉深筋参数化的设计方法，采用自适应的曲线离散方法得到控制点，再基于扫略的方法建立拉深筋模型。熊洋等[5]提出了可编辑的参数化建模方案，并设计了基于UG 的二次开发工具。王振等[6]采用正交截面法创建拉深筋截面线，有效解决了负角的问题。尹雁飞等[7]开发了可参数化建模的拉深筋设计模块。郑刚等[8]引入响应面方法和遗传算法建立了基于近似模型的拉深筋截面几何参数的求解模型。

这些参数化拉深筋设计方法，是借助软件扫描式的建模方法，其建模精度受到软件的限制，且扫描截面需要合理选取才能成功。以下求解了拉深筋截面参数的数学理论公式并采用了参数化的设计方法，即在三维设计软件中直接拉深立壁再倒圆角的设计方法，其建模精度高、不受软件限制、不受拉深筋中心线曲率变化影响，且可以做成软件的二次开发使用，只需要输入初始参数，即可自动计算设计拉深筋所需的参数。

1 Z向方形筋截面参数理论求解

1.1 Z向方形筋截面参数的几何约束关系

Z向方形筋控制截面形状的关键参数如图1 所示，其中参数含义及约束关系如下所述。

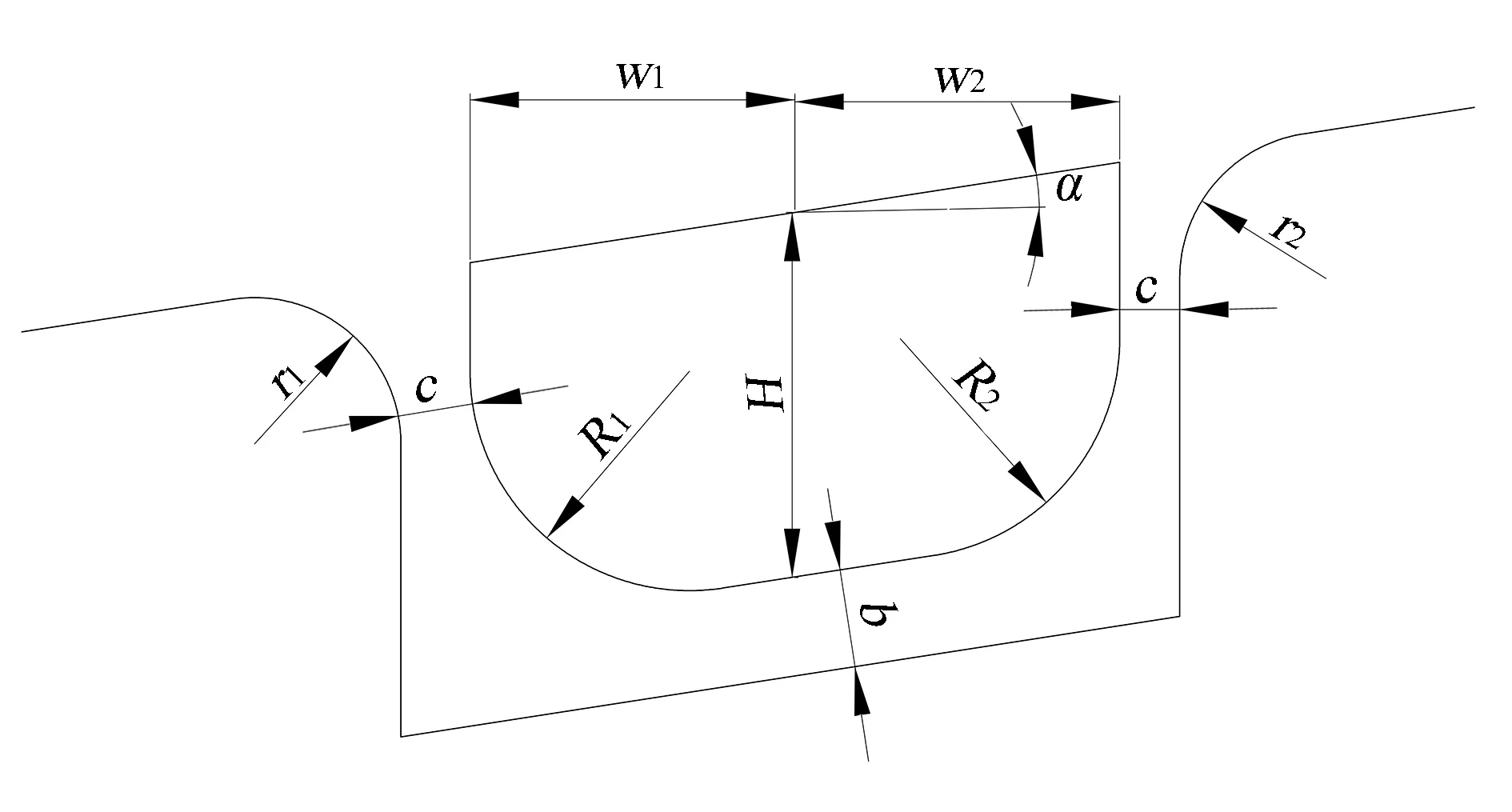
图1 Z向方形筋的截面参数

（1）w1和w2分别为流入、流出方向的筋宽，为沿Z向投影的宽度，且满足恒等关系w1=w2，在求解过程中用w表示设定的理论筋宽。

（2）H为筋高，且为沿Z向的高度。

（3）R1和R2分别为流入、流出方向的凸筋圆角，当筋高较低时R1不一定等于R2；在求解过程中用R表示设定的理论凸筋圆角。

（4）r1和r2分别为流入、流出方向的凹筋圆角，且r1=r2。

（5）c为凸、凹筋的间隙值，筋较高时为凸、凹筋立面的间隙值，筋较低时为凸、凹筋圆角的最小间隙值。

（6）b为凸、凹筋底部间隙值。

（7）α为压料面的倾角，是压料面的特征值，而非自行设定的参数值，此处设定α≥0。

1.2 3D软件设计Z向方形筋截面参数的求解

在使用3D 软件设计Z向方形筋时，需要的关键参数如图2 所示。为了便于分析与说明，将凸筋分为流入方向和流出方向分别计算。在流入方向，存在的几何约束关系为d1≥0，由此R1便存在极大值，其数学关系式为：

图2 使用3D软件设计Z向方形筋的关键参数

设定R1判据为R1max，则有以下式（2）关系：

在流入方向，只有当筋较高时，e1≥0，此时e1求解公式为式（3）：

由以上（1）～（3）公式，可得到用3D 软件设计Z向方形筋流入侧的参数，如式（4）、式（5）：

其中，R1为凸筋流入侧圆角大小；Xin为凸筋流入侧立壁与拉深筋中心线在Z向投影的距离。同样地，可得流出侧的几何约束关系d2≥0，即：

设定R2判据为R2max，则有以下式（7）关系：

在流出方向，只有当筋较高时，e2≥0，此时e2求解公式为式（8）：

由以上式（6）～（8）可得到用3D软件设计Z向方形筋流出的参数，如式（9）、式（10）：

其中，R2为凸筋流出侧圆角大小；Xout为凸筋流出侧立壁与拉深筋中心线在Z向投影的距离。

2 法向方形筋截面参数理论求解

2.1 法向方形筋截面参数的几何约束关系

法向方形筋控制截面形状的关键参数如图3所示，其中参数含义及约束关系如下所述。

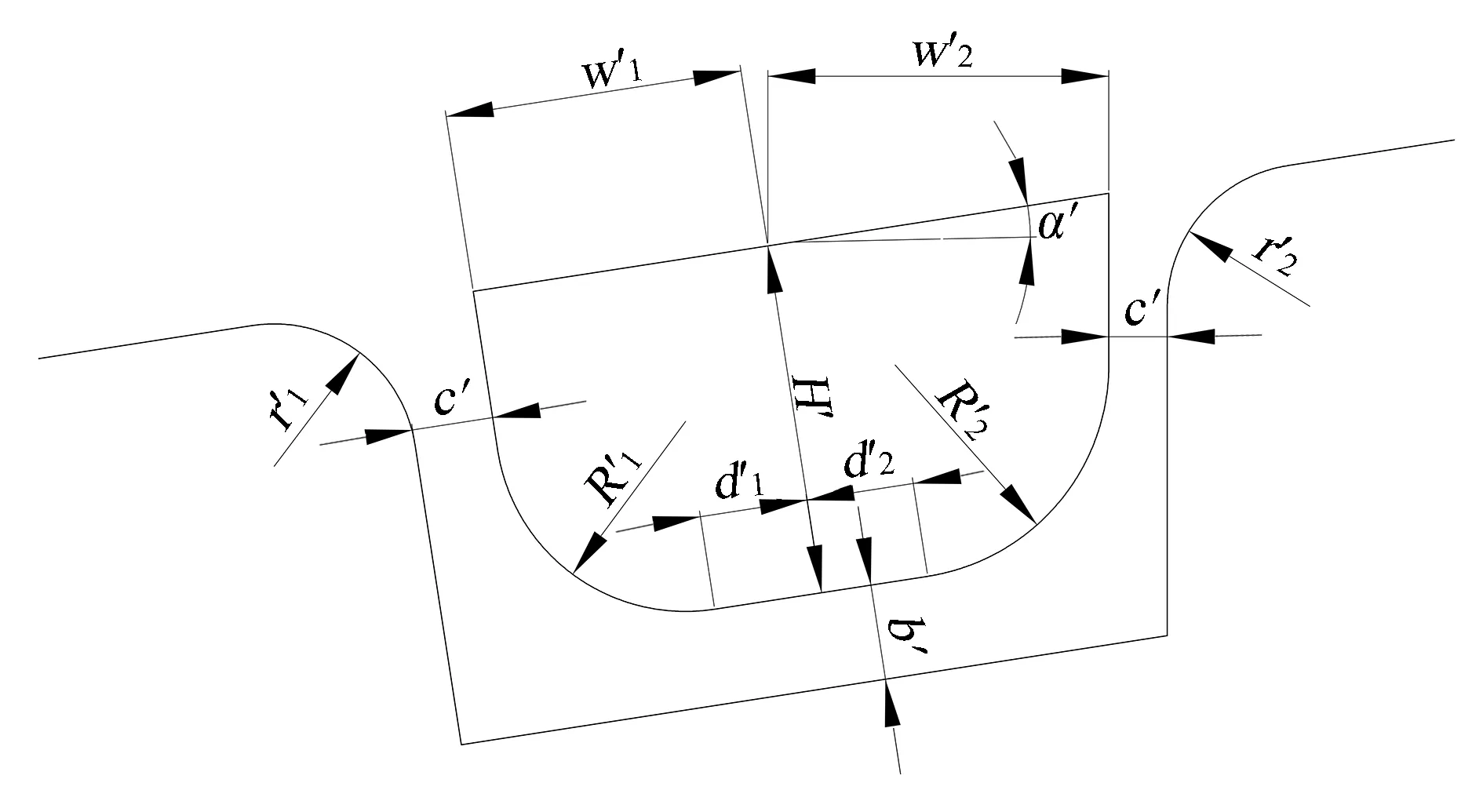
图3 法向方形筋的截面参数

（1）w′1和w′2分别为流入、流出方向的筋宽，w′1为法向投影的宽度，w′2为Z向投影的宽度，w′1和w′2无特定恒等关系，在求解过程中用w′表示设定的理论筋宽。

（2）d′1和d′2分别为流入、流出方向凸筋剩余宽度，且d′1=d′2≥0。

（3）H′为筋高，且为沿法向的高度。

（4）R′1和R′2分别为流入、流出方向的凸筋圆角，且满足恒等关系R′1=R′2；在求解过程中用R′表示设定的理论凸筋圆角。

（5）r′1和r′2分别为流入、流出方向的凹筋圆角，且r′1=r′2。

（6）c′为凸、凹筋的间隙值，筋高较高时为凸、凹筋立面的间隙值，筋高较低时为凸、凹筋圆角的最小间隙值。

（7）b′为凸、凹筋底部间隙值。

（8）α′为压料面的倾角，是压料面的特征值，而非自行设定的参数值，此处设定α′≥0。

2.2 3D软件设计法向方形筋截面参数的求解

在3D 软件设计法向方形筋时，与Z向方形筋类似，分别计算流入侧和流出侧的参数，如图4 所示。根据几何约束关系d′1=d′2≥0，可得R′1存在极大值，其判据数学表达式为：

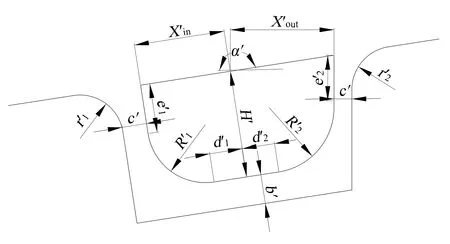
图4 使用3D软件设计法向方形筋时的关键参数

在流入方向，筋的高度判据e′1表达式为：

由以上（11）、（12）公式，可得到用3D 软件设计法向方形筋时的流入侧的参数：

其中，R′1为凸筋流入圆角大小；X′in为凸筋流入侧法向立壁与拉深筋中心线的距离。

根据法向筋的几何约束关系d′1=d′2≥0，可得流出侧R2极大值的判据为：

在流入方向，筋的高度判据e′2表达式为：

由以上（15）、（16）公式，可得到用3D 软件设计法向方形筋时的流出侧参数：

其中，R′2为凸筋流出圆角大小；X′out为凸筋流出侧Z向立壁与拉深筋中心线的距离。

3 半圆形拉深筋截面参数理论求解

3.1 半圆形拉深筋截面参数的几何约束关系

半圆形拉深筋无论凹筋为Z向还是法向，其凸筋均按照法向求解，其控制截面形状的关键参数如图5所示，其中参数含义及约束关系如下所述。

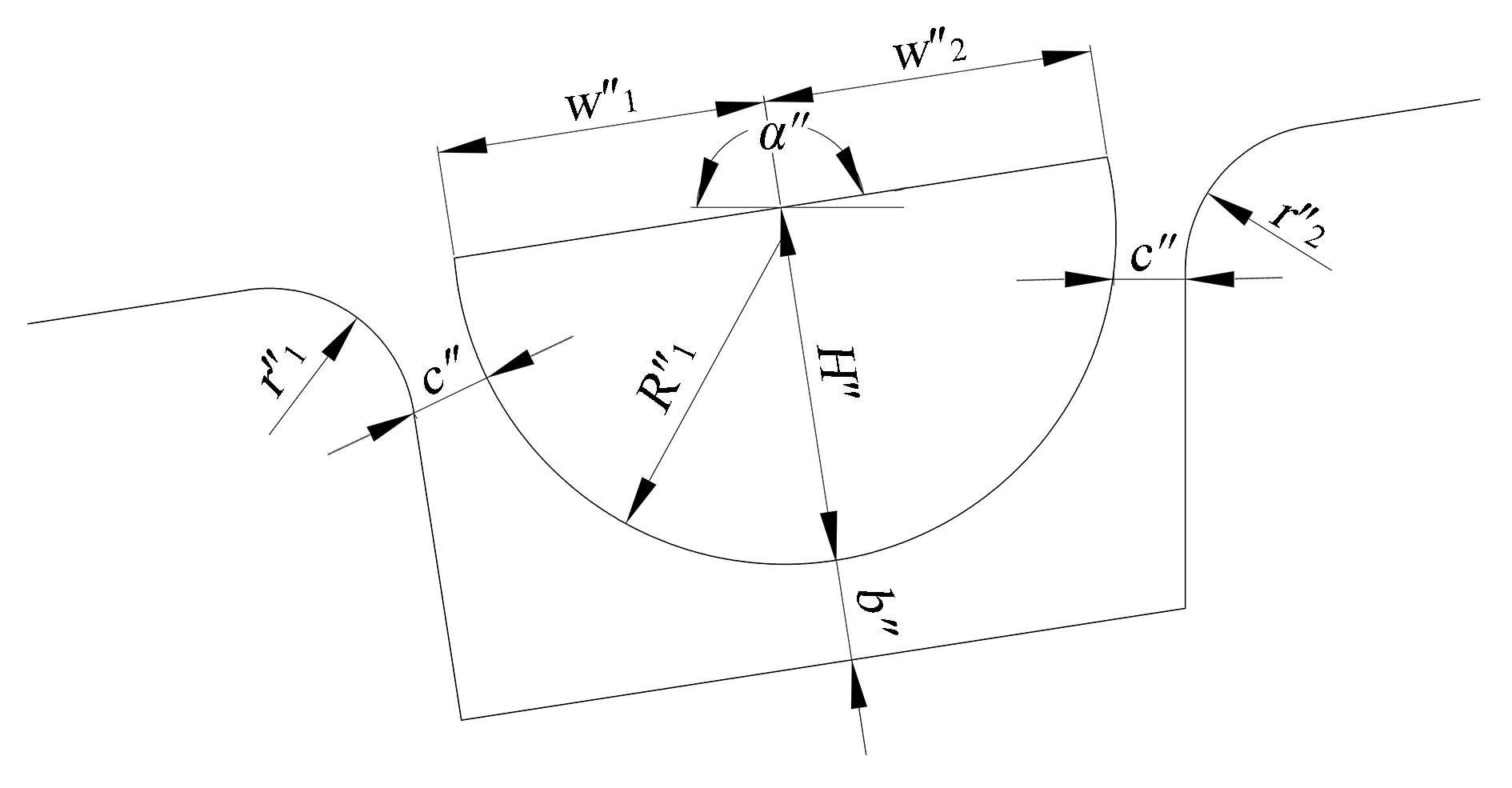
图5 半圆形拉深筋截面参数

（1）w″1和w″2分别为流入流出方向的筋宽，且满足恒等关系w″1=w″2，且均为理论设定宽度w″。

（2）H″为筋高，且为沿法向的高度。

（3）r″1和r″2分别为流入流出方向的凹筋圆角，且r″1=r″2。

（4）c″为凸、凹筋的间隙值。

（5）b″为凸、凹筋底部间隙值。

（6）α″为压料面的倾角，半圆形筋截面参数与倾角α″无关。

3.2 3D软件设计半圆形拉深筋截面参数的求解

在使用3D软件设计圆筋时，需要的关键参数如图6所示，其中：

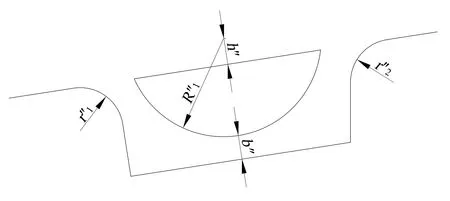
图6 使用3D软件设计半圆形筋时的关键参数

其中，R″1为设计时用的凸筋圆角；h″为凸筋圆角中心距离压料面的法向距离。

以上无论是Z向方形筋还是法向方形筋，或是半圆形筋，其求解公式均为去除料厚的真实值，在3D软件中进行筋设计时需要考虑料厚和基准侧，若为上型基准，则压边圈上的凹筋参数增加料厚t；若为下型基准，则上模凸筋的参数增加料厚t。

同时，以上的求解公式不包含凹筋的截面参数，因为在3D设计软件中可以将凸筋向外偏置间隙值c后，再将压料面倒角（凹筋流入流出角），最后拉深凹筋立面即可得到最终凹筋形状。3D 软件设计拉深筋时，凸、凹筋的间隙值c与料厚无关。

4 某汽车后背门内板3D筋拉深模拟验证

以某汽车后背门内板为例进行验证，其中拉深形式为三动拉深，上、下压边圈的压边力分别为1 150 kN 和2 800 kN，采用内外双圆筋拉深，摩擦系数为0.14，板料材质为Baosteel-CR4 GI，料厚为0.7 mm，轧制方向为0度。

3D 拉深筋借助CATIA 的Power Copy 功能，用截面参数理论求解公式进行制作，不同段的筋用桥接命令接顺，并将尖角处理为半径2 mm 的倒角，如图7所示。

图7 使用Power Copy制作3D拉深筋

拉深筋最主要的作用是控制板料的流入量，用理论公式制作的拉深筋流入量与AutoForm 自动生成的3D 拉深筋流入量和实际出件的关键位置流入量进行对比，如表1所示，其关键位置如图8所示。

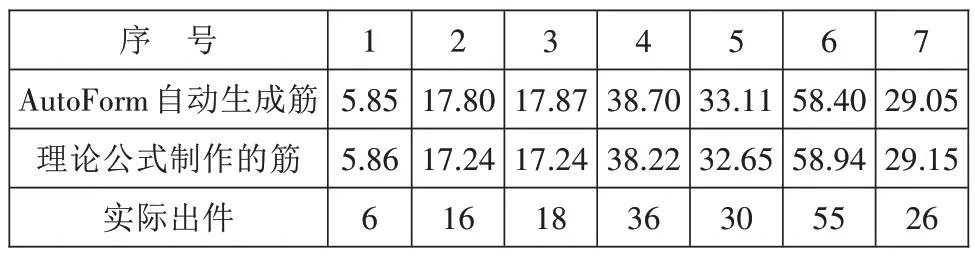
表1 拉深件关键位置流入量对比 mm

图8 流入量的关键位置

拉深成形性结果对比如图9、图10所示，其中图9分别为AutoForm 自动生成筋的减薄率和用理论公式制作筋的减薄率；图10所示分别为AutoForm自动生成筋的最大失效和用理论公式制作筋的拉深最大失效。

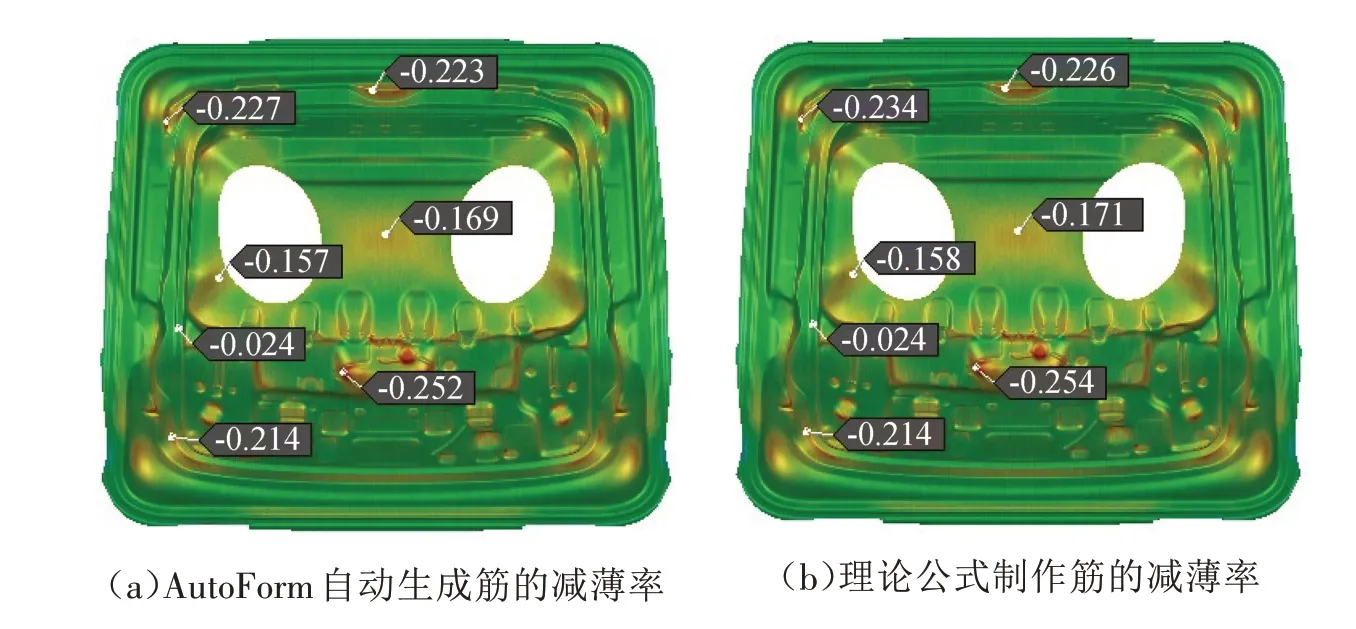
图9 减薄率对比

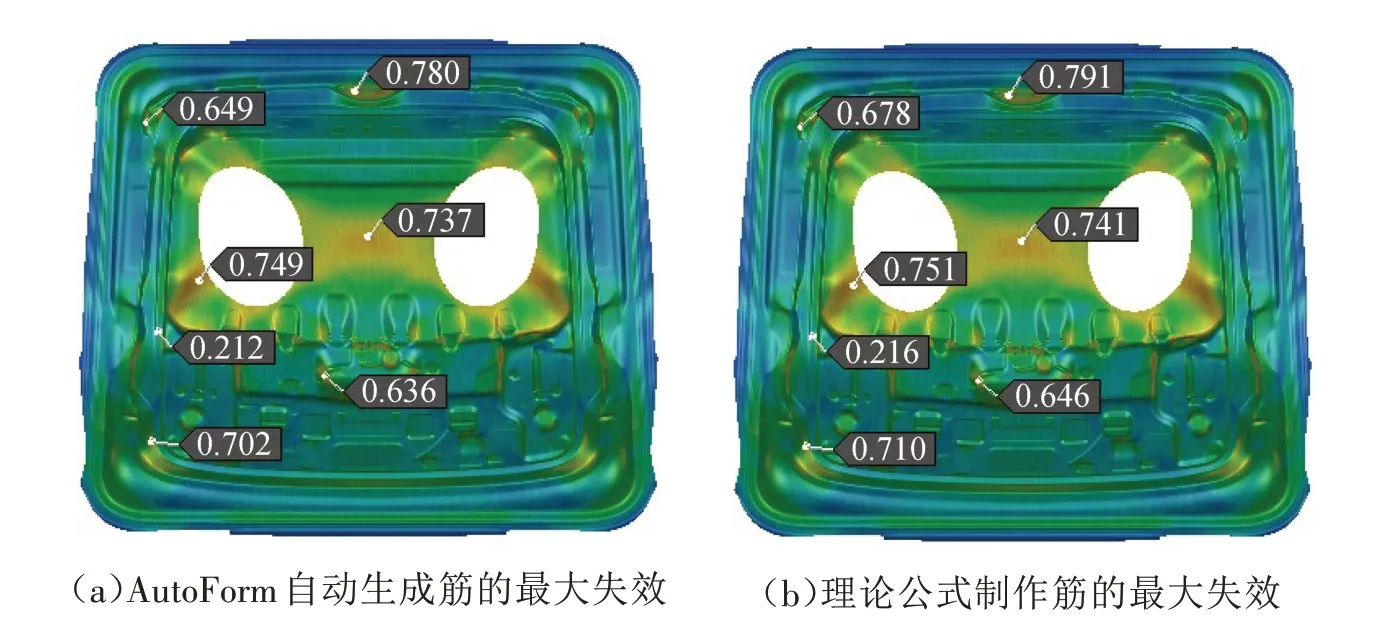
图10 最大失效对比

5 结束语

介绍了Z向方形拉深筋、法向方形拉深筋、半圆形筋的截面参数的几何约束关系，求解了3D软件设计拉深筋的数学理论公式，并根据此公式在CATIA中借助Power Copy 功能实现了带参数的拉深筋设计。应用理论公式设计的3D 拉深筋使用AutoForm有限元分析软件进行分析，其拉深结果与AutoForm自动生成拉深筋的拉深结果进行对比，流入量、减薄率、最大失效等结果均较为一致，验证了所提出的理论公式求解拉深筋截面参数方法的有效性。