大面积矩形感性耦合等离子体源的三维流体力学模拟1)

赵明亮 张钰如 高 飞 宋远红 王友年

(大连理工大学物理学院,三束材料改性教育部重点实验室,辽宁大连 116024)

引言

与阴极射线管(cathode ray tube,CRT)显示器相比,平板显示器(flat panel display,FPD)具有更轻薄、易携带、无辐射和分辨率高等优点,因此平板显示器已经成为目前主流的显示器[1-2],并被广泛应用于电视、电脑和手机中.大面积的平板显示器是由薄膜晶体管(thin film transistor,TFT)阵列组成的[3],在其制作过程中,需要用到等离子体刻蚀和薄膜沉积工艺,如使用碳氟-氧混合气体放电产生的等离子体对氧化硅薄膜进行刻蚀[4].另外,等离子体源也被广泛应用于光伏产业中,如太阳能电池的制备.目前最常用的太阳能电池是硅太阳能电池[5],在其制作过程中,同样需要用到多种等离子体处理工艺,如薄膜钝化工艺[5].

用于刻蚀和薄膜沉积工艺的等离子体源主要有两种类型,分别为容性耦合等离子体(capacitively coupled plasma,CCP)源与感性耦合等离子体(inductively coupled plasma,ICP)源[6-9].以平板显示工艺的发展为例,在第6 世代工艺之前,面板的面积一般不超过 1500 mm×1800 mm,所使用的等离子体源主要为CCP 源,放电频率为13.56 MHz[10-11].由于此时面板的横向尺寸远远小于电磁波的波长,驻波效应并不显著[12-14],等离子体的空间分布也较为均匀.然而,随着平板显示工艺的发展,面板的面积越来越大,如第8.5 世代工艺的面板面积已经增加到2200 mm×2500 mm[10].此时,CCP 源中的驻波效应非常明显,已经严重影响了等离子体的均匀性,进而降低了产品的性能[10].目前,还没有特别有效的手段来抑制驻波效应[15-17].因此,为了保持放电的均匀性,人们又提出了新一代的等离子体源,即大面积矩形ICP源[10,18].与CCP 源相比,ICP 源具有很多优点,例如:(1) ICP 源具有较高的密度,因此可以获得较高的刻蚀和薄膜沉积速率;(2) ICP 源可以在低气压环境下放电,如几帕到数十帕;(3) 通过在下极板上施加射频偏压,可以实现对入射到极板上的离子通量和离子能量的独立调控;(4) ICP 源的结构较为简单,容易扩展为大面积腔室[6,11].

与大面积CCP 源相比,尽管ICP 源中的驻波效应较弱,保持较好的等离子体均匀性仍是大面积矩形ICP 放电中的一个至关重要的问题.这是因为等离子体密度的空间分布直接影响刻蚀和薄膜沉积过程的均匀性,进而影响平板显示器和太阳能电池等产品的性能.因此,优化大面积矩形ICP 源的放电参数和射频线圈的结构,进而提高等离子体的均匀性,对于改善等离子体处理工艺具有重要的意义.

由于数值模拟技术具有成本低、输出信息多等优势,其被广泛应用于等离子体源的优化设计和等离子体特性的分析中[19-22].虽然人们已经对ICP 源进行了大量的模拟研究,但是大部分的工作都是针对半导体工艺中常用的圆柱形感应耦合等离子体腔室,即采用的是二维轴对称模型[23-26].然而,平板显示工艺和光伏工艺中所采用的ICP 源通常具有矩形结构,因此必须进行三维模拟,才能满足实际需求.由于受到计算效率的限制,目前关于矩形ICP 源的数值模拟研究十分有限.韩国Song 等[3]针对矩形ICP 腔室,建立了电磁场对等离子体加热的理论模型,通过对感应电场的波动方程进行解析求解,得到了电场和磁场的空间分布.然而,他们的模型并不是自洽的,即模型中假设等离子体是均匀分布的,且密度为定值.Lee 等[4]利用COMSOL 研究了矩形感性耦合CF4/O2等离子体中,离子和中性粒子密度的空间分布以及离子通量.然而,由于模型中采用迁移扩散近似来描述离子的运动过程,该模型在低气压条件下并不十分准确.Oh 等[27]同样基于COMSOL 研究了大面积三维矩形感性耦合Ar 等离子体的特性,结果表明电子密度主要受到线圈电流和气压的影响,而电子温度和电势主要与气压有关.此外,他们还发现在Ar/Cl2混合气体放电中,吸收功率、电子温度、电势均随着Cl2含量的增加而降低,但电子密度几乎不变[28].

为了加深对大面积矩形感性耦合等离子体源的理解,为设计线圈结构、优化放电参数、提高等离子体均匀性提供指导,本文采用自主开发的三维流体力学模型,对大面积矩形感性耦合放电过程进行了模拟研究.本文的内容安排如下: 第1 部分详细介绍了三维流体力学模型;第2 部分针对氩气放电,给出了不同放电参数和线圈结构下等离子体密度的空间分布,并对结果进行分析;最后,对本文的研究结果进行小结.

1 流体力学模型

模拟中采用的矩形感性耦合等离子体源的腔室结构如图1 所示,其中腔室的长度为200 cm,宽度为160 cm,等离子体区域的高度为30 cm,介质窗的厚度为1 cm,射频线圈放置在介质窗上方,屏蔽罩的高度为10 cm,坐标原点位于腔室底部中心处.本文研究了两种不同的线圈结构,分别是矩形盘香型线圈和矩形阵列线圈,如图2 所示.放电气体为氩气,连接线圈的射频电源频率为13.56 MHz.

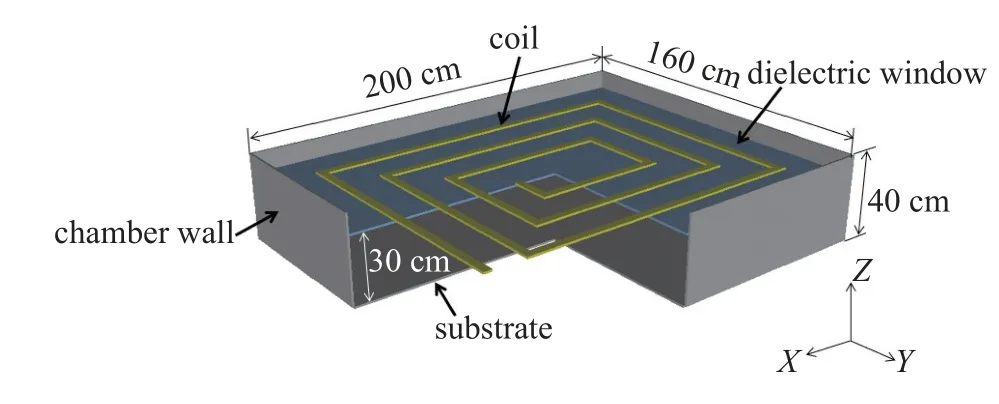
图1 腔室结构示意图Fig.1 Schematic diagram of the chamber structure

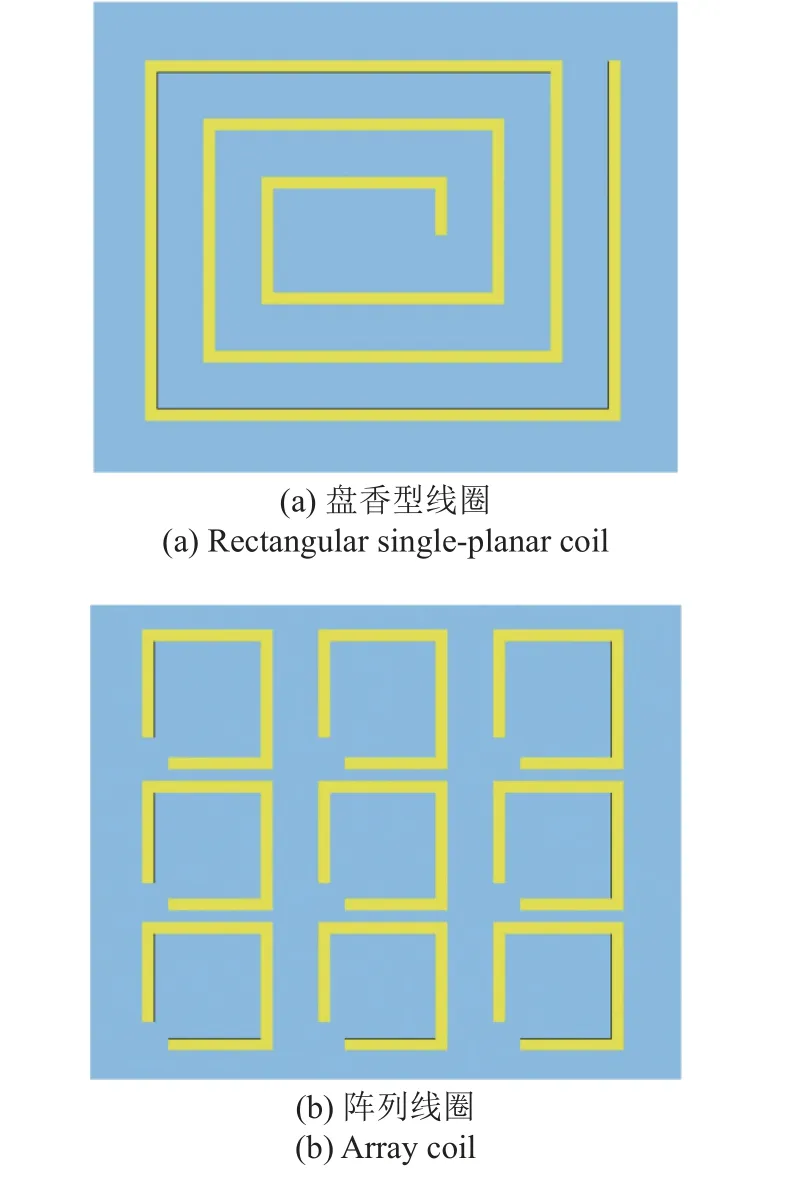
图2 线圈结构示意图Fig.2 Schematic diagram of the coil structure

1.1 电磁场模块

感性耦合等离子体源,是由线圈中的射频电流激发出来的感应电场维持放电的.为了提高模拟效率,我们采用频域有限差分法(finite difference frequency domain,FDFD)来求解线圈电流产生的感应电磁场[29].腔室中的感应电场E和感应磁场B满足如下的麦克斯韦方程组

其中 µ0是真空磁导率,ε0为真空介电常数,µr和εr分别是相对磁导率和相对介电常数.在模拟中,通过不断调整线圈的电流密度Jcoil,使得等离子体的吸收功率等于设定值.Jp是等离子体的极化电流密度,满足如下方程

其中e是元电荷,ne是电子密度,me是电子质量,ven是电子与背景气体的碰撞频率.

对方程(1)两边取旋度,并利用方程(2),可以得到

对于感应电场,假设其散度为零,且所有的物理量都是以射频源的角频率 ω 随时间作简谐变化,这样可以把方程(4)和(3)简化为

基于上述求得的感应电场和等离子体极化电流,可以计算出感应沉积功率密度

1.2 流体模块

流体模块用于确定等离子体中各种粒子的密度、电子温度、双极静电场和离子通量等参数.其中,离子密度满足如下的连续性方程

式中,ni,ui和Si分别表示离子的密度、速度和源项.由于感性耦合等离子体源常常工作在低气压条件下(小于1 Pa),不能忽略离子的惯性作用,因此采用如下的离子动量方程来描述离子速度

其中mi是离子 质量,qi是离子 电荷,Es是双极静电场,kB是玻尔兹曼常数,Ti是离子温度(本文中设定离子温度为330 K),Mi表示离子与背景气体碰撞引起的动量转移.

由于没有偏压电源的存在,可以假设等离子体满足准电中性条件,即电子密度ne等于离子密度ni

电子通量 Γe由迁移扩散近似条件确定,即

其中 µe=e/(meven) 是电子的迁移率,De=kBTe/(meven)是电子的扩散系数.在双极扩散近似(电子通量等于离子通量)下,可以得到双极静电场的表达式

最后,根据电子的能量守恒方程,可以确定出电子的温度Te

其中Ke是电子的热传导系数.

对于中性粒子的密度nn,可以由如下扩散方程确定

其中Dn是中性粒子的扩散系数,Sn是中性粒子的源项.Γn是 中性粒子的扩散通量,其形式为 Γn=-Dn∇nn.

1.3 计算区域与边界条件

图3 为计算区域的示意图.流体模块的计算区域只包括区域1,即等离子体区域;电磁模块的计算区域包括区域1、区域2 以及区域3.另外,以上方程必须在适当的边界条件下才能准确地描述放电过程.对于感应电场,假设器壁为理想导体,因此平行于器壁的电场分量等于零.此外,边界处的离子速度等于玻姆速度uB=(kBTe/mi)1/2,方向指向侧壁;离子的密度连续,即 ∇ni·en=0;电子的热通量满足Qe=2kBTeΓe;中性粒子的通量满足且方向指向边界,其中Tn=330 K 是中性粒子的温度,mn是中性粒子的质量.

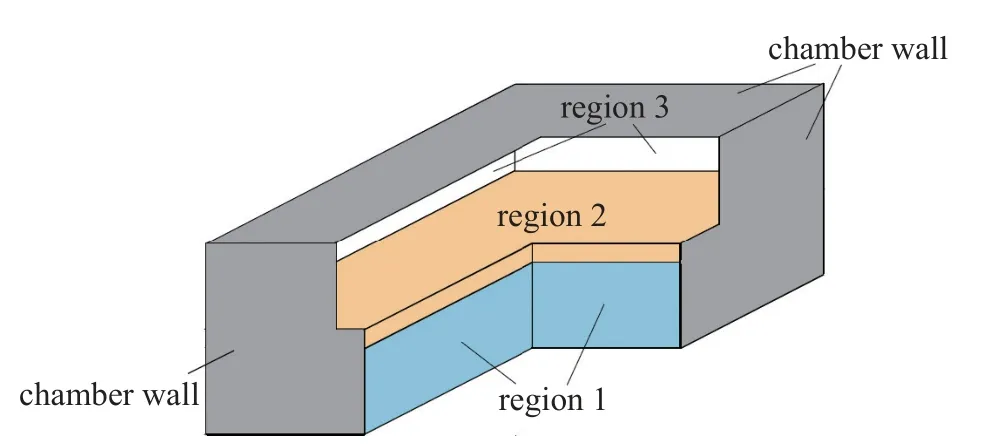
图3 计算区域示意图Fig.3 Schematic diagram of the calculation region

1.4 碰撞过程

本文以氩气放电为例,模型中考虑了6 种碰撞,分别为电子与基态原子的弹性碰撞、激发碰撞和电离碰撞(编号1,2,3),电子与亚稳态原子的电离碰撞和退激发碰撞(编号4 和5),以及亚稳态原子之间的电离碰撞(编号6),如表1 所示.

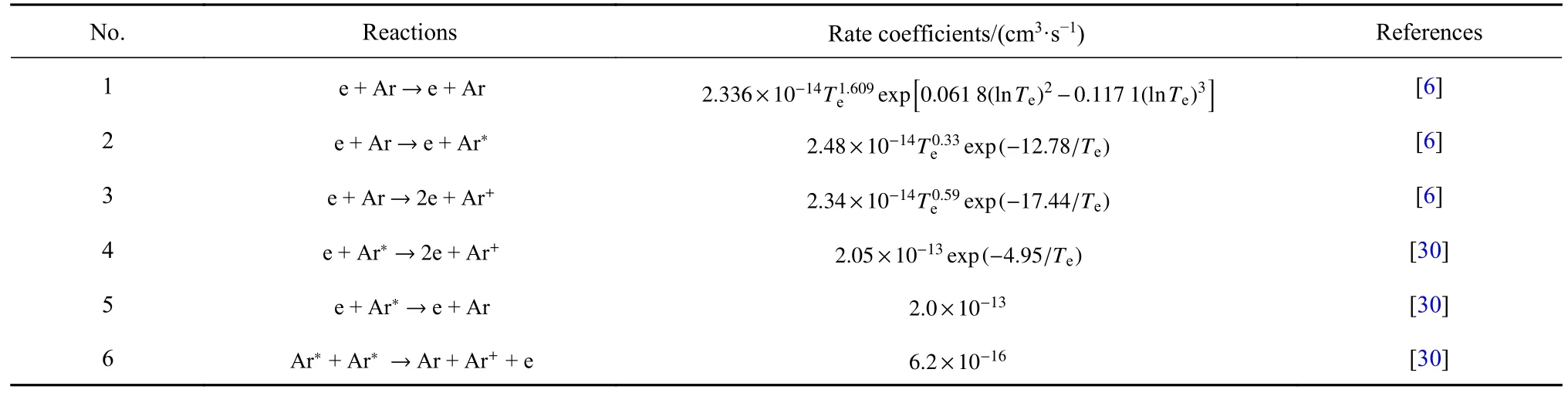
表1 氩等离子体中的碰撞反应及速率系数Table 1 Collision reactions and rate coefficients in argon plasma

1.5 数值方法

采用有限差分法对上述方程进行求解,模拟中使用的网格如图4 所示.由于在电磁场模块中采用频域有限差分方法,每个射频周期只需要求解一次电磁场.此外,对于电子能量方程、离子连续性方程和离子动量方程,在时间上均采用显式方法进行求解.对于离子动量方程中的电场力项,使用迎风格式进行离散,而其他项均采用中心差分进行离散.

图4 网格划分示意图Fig.4 Schematic diagram of the grid

2 结果与讨论

在本小节,我们首先介绍等离子体状态参数的三维空间分布.然后,讨论不同放电功率(1000,2000,3000 和4000 W)和气压(4,12 和20 mTorr)下,等离子体密度和电子温度的空间分布.最后,分析阵列线圈对等离子体均匀性的影响.

2.1 等离子体参数的三维空间分布

图5 给出了电子密度、电子温度、感应沉积密度以及激发态氩原子密度的三维空间分布,其中放电气压为4 mTorr,功率为1000 W,线圈结构为盘香型.

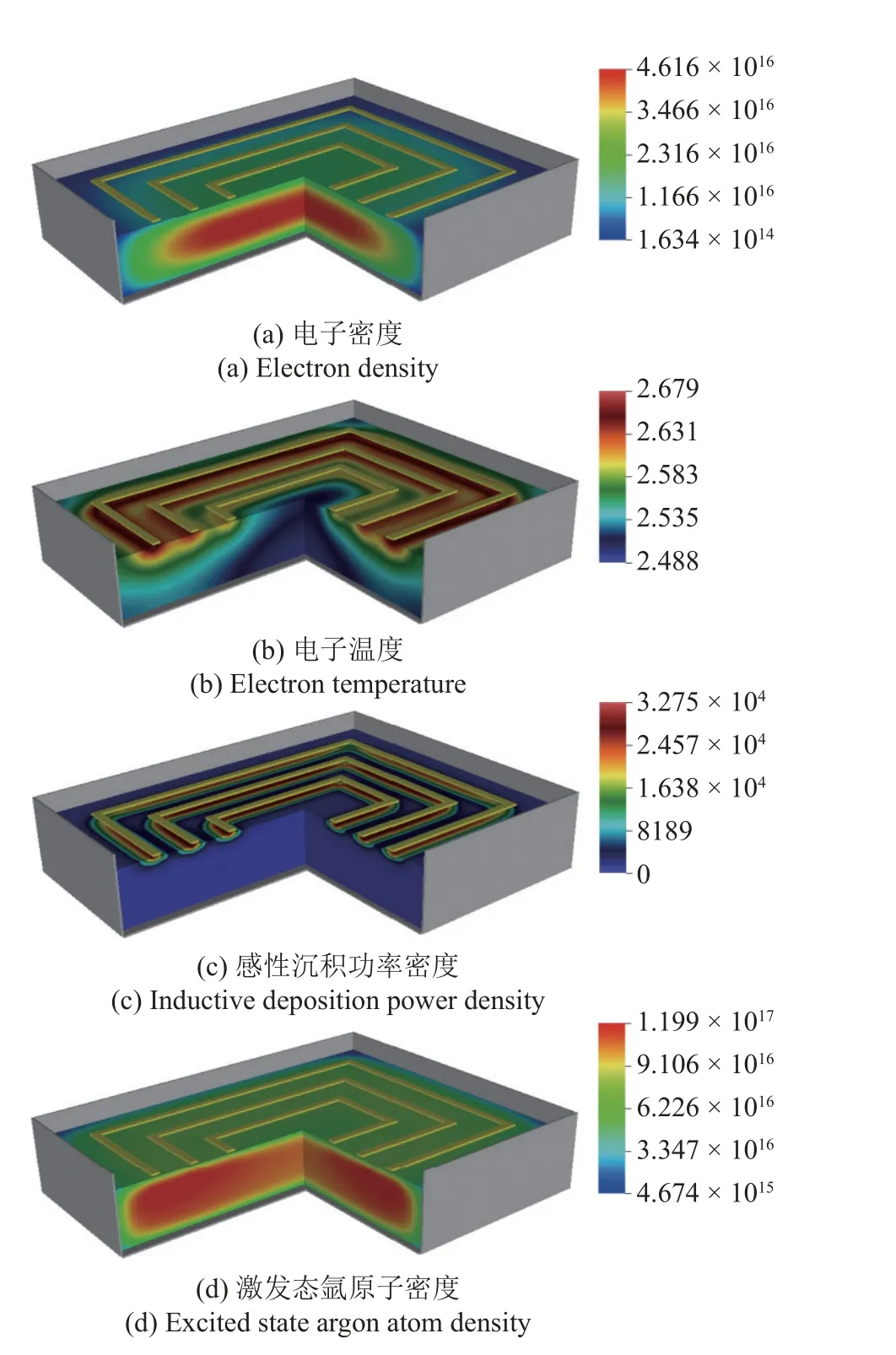
图5 等离子体参数的三维空间分布Fig.5 Three-dimensional spatial distribution of the plasma parameters

从图5(a)可以看出腔室中心区域的电子密度较高且分布比较均匀,而在靠近侧壁处电子密度显著下降.这是因为在低气压(4 mTorr)下,带电粒子与背景中性气体的碰撞频率很低.因此,输运过程对等离子体的空间分布起主导作用,即电子和离子不断往腔室中心处聚集.图5(b)是电子温度的三维空间部分,可以观察到电子温度的最大值出现在线圈下方.这是由于感性功率主要沉积在线圈下方(如图5(c)所示),即电子主要在线圈下方被加热.此外,感性沉积功率主要集中在介质窗下方一个很薄的区域内,这是由趋肤效应导致的.激发态氩原子的密度分布(图5(d))与电子温度类似,即最大值也是出现在线圈下方,这是因为此处的电子温度较高、激发速率较大.

2.2 功率的影响

图6 为不同功率下,在y=0 cm,z=15 cm 处,电子密度和电子温度在x方向的一维分布,其中气压固定为4 mTorr.从图6(a)中可以看出,随着功率从1000 W 增加到4000 W,电子密度提高,这是因为中性气体的电离过程有所增强.此外,在氩气放电中,由于电子温度主要与气压以及腔室尺寸有关,而与功率几乎无关,电子温度随功率几乎不变,如图6(b)所示[6].另外可以看到,功率对于电子密度的空间分布几乎没有影响,即在不同的功率下,电子密度在x=0 m 附近有微弱的下凹,总体上呈现出中间区域高两侧低的分布.

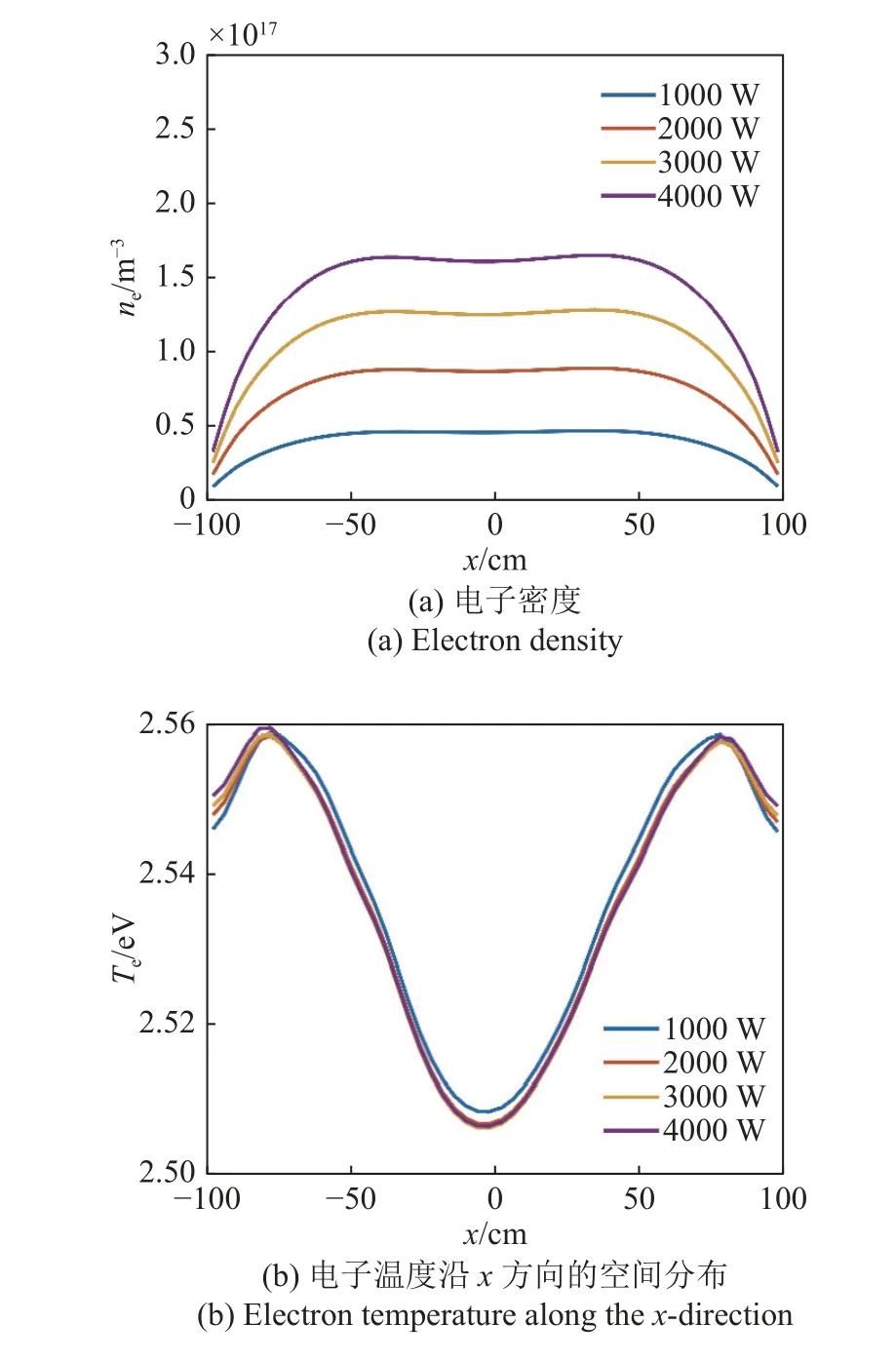
图6 不同功率下,在y=0 cm,z=15 cm 处,(a)电子密度和(b)电子温度沿x 方向的空间分布,其中放电气压为4 mTorrFig.6 Spatial distribution of (a) electron density and (b) electron temperature along the x-direction at y=0 cm and z=15 cm at different powers.The pressure is 4 mTorr

2.3 气压的影响

图7 为不同气压下(4 mTorr,12 mTorr 以及20 mTorr),电子密度在z=3 cm 平面内的空间分布,其中功率固定为1000 W.从图中可以看出,随着气压的增加,电子密度的均匀性明显下降.如当放电气压为4 mTorr 时,电子密度的最大值出现在腔室的中心区域,且空间分布比较均匀.当放电气压增加到20 mTorr 时,中心处的电子密度有所下降,即电子密度的最大值分布在腔室中心的周围,此时等离子体的均匀性明显下降.这是因为一方面,当气压较高时,电子与背景中性粒子的碰撞频率增加,带电粒子的扩散和迁移过程均受到抑制;另一方面,线圈下方的电子温度最高,电离过程最强,因此电子主要产生在靠近线圈的位置.

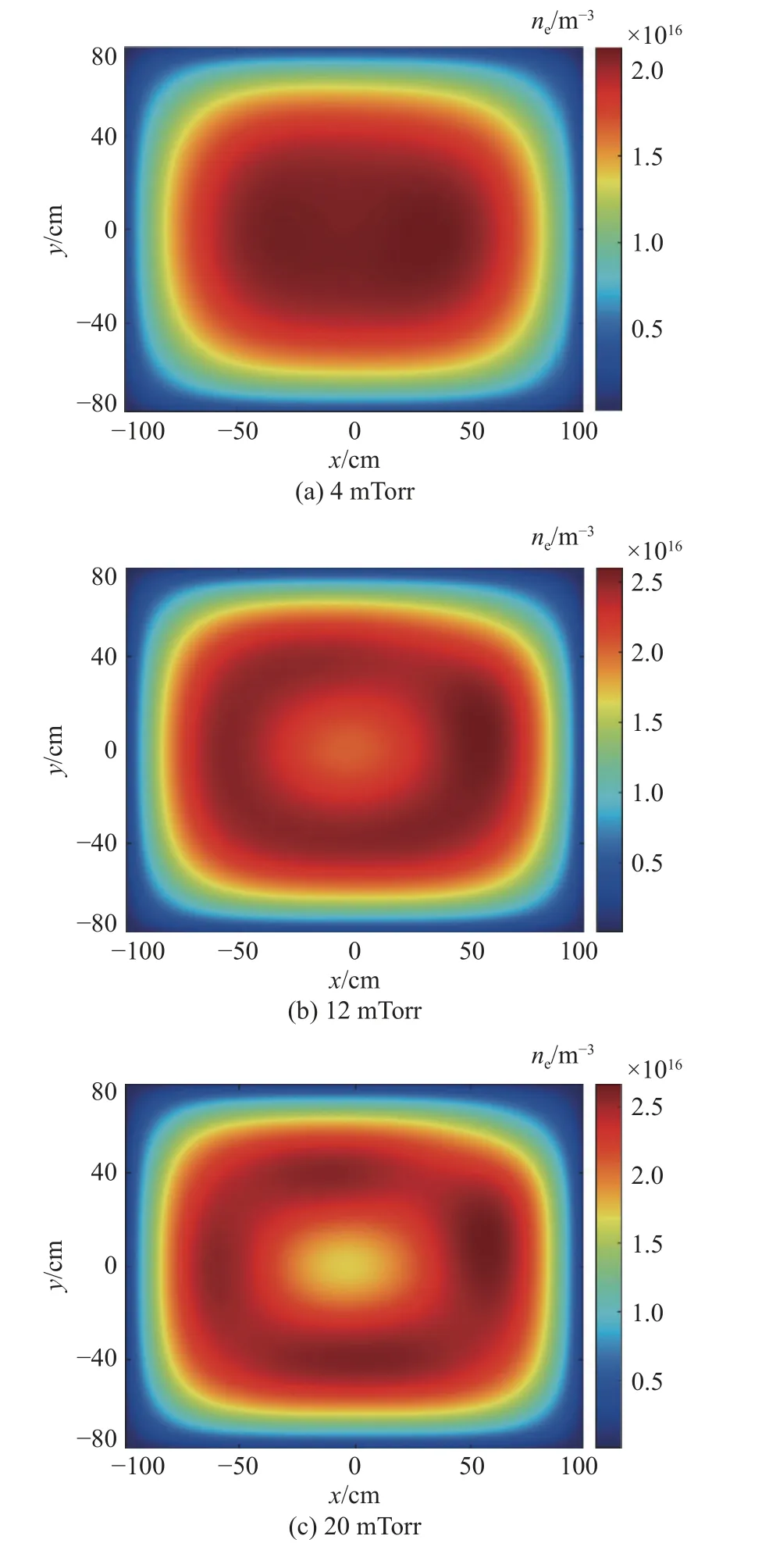
图7 不同气压下z=3 cm 平面内电子密度的空间分布,其中放电功率为1000 WFig.7 Spatial distribution of electron density in the plane z=3 cm at different gas pressures.The discharge power is 1000 W

2.4 线圈结构的影响

最后,为了说明线圈结构对于等离子体均匀性的影响,我们对比了盘香型线圈和阵列线圈结构下,电子密度的空间分布,如图8 所示.其中,放电气压为20 mTorr,功率为1000 W.可以看到,由于此时的气压较高,电子密度的分布变得局域,即密度最大值出现在线圈下方区域.通过对比可以发现,采用阵列线圈得到的电子密度分布比盘香型线圈更均匀,这是因为阵列线圈的排布使得电磁场及感性功率密度具有较为均匀的分布.

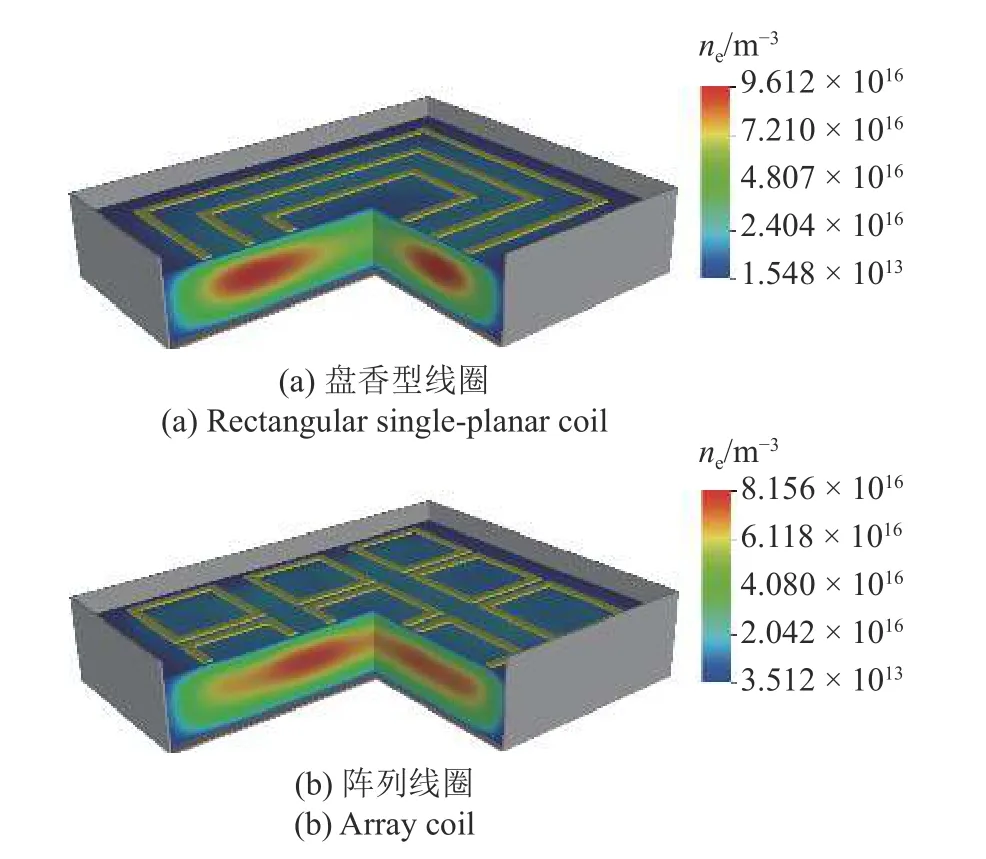
图8 不同线圈结构下,电子密度的三维空间分布Fig.8 Three-dimensional spatial distribution of electron density under different coil structures

为了更清楚地分析线圈结构对于均匀性的影响,图9 给出了两种线圈结构下,电子密度在X-Y平面上的分布(z=2,15,28 cm).图9(a)～ 图9(c)为盘香型线圈结构下,电子密度在X-Y平面上的分布,图9(d)～ 图9(f)为阵列线圈结构下电子密度在X-Y平面上的分布.当线圈形状为盘香型线圈时,电子密度在X-Y平面上呈现出明显的环状分布,类似于线圈的形状.然而,当线圈形状为阵列线圈时,电子密度在X-Y平面上的均匀性显著提高.这是因为当放电气压较高时,电子密度的分布由输运过程和电子产生的位置共同决定.因为阵列线圈在X-Y平面内的排布更加均匀,所以电子产生的比较均匀.另外,下极板附近(z=2 cm)的电子密度分布对刻蚀和沉积过程有直接的影响,从图9(a)和图9(d)中可以看出,当线圈为盘香型线圈时,即使在远离线圈的平面内,电子密度的分布仍然存在很明显的不均匀性,这不利于刻蚀和沉积的均匀性.相比之下,阵列线圈放电保证了下极板附近电子密度分布的均匀性.

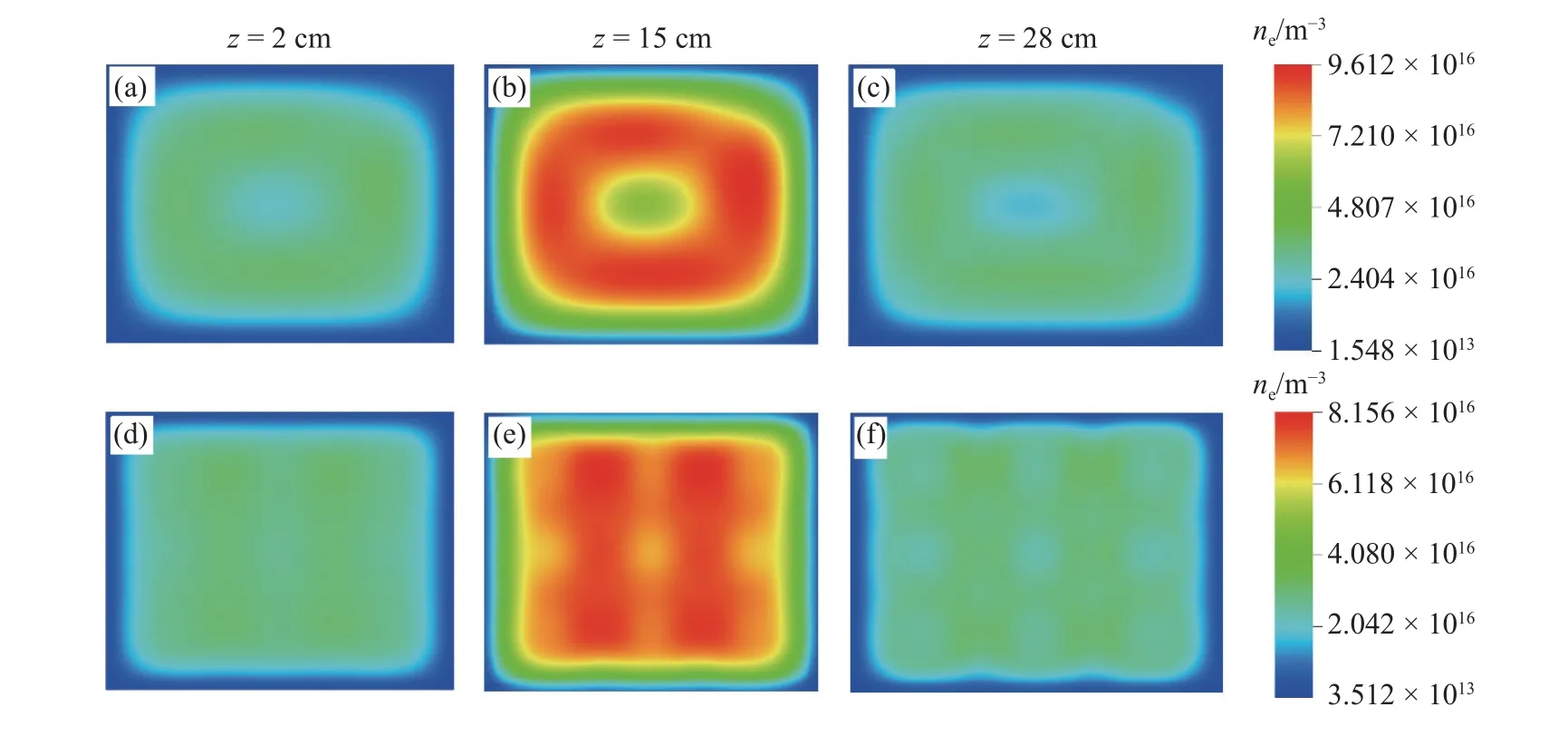
图9 不同线圈结构下,电子密度在z=2,15,28 cm 平面内的分布.(a)～ (c)对应盘香型线圈,(d)～ (f)对应阵列线圈Fig.9 Spatial distribution of electron density in the z=2,15,and 28 cm planes for different coil structures.(a)～ (c) correspond to rectangular singleplanar coil,and (d)～ (f) correspond to array coil

3 结论

本文利用自主开发的三维等离子体流体力学模型,研究了大面积矩形感性耦合等离子体的放电特性.研究结果表明,在低气压(4 mTorr)下,电子密度的最大值出现在矩形腔室的中心区域,而电子温度、激发态氩原子密度以及感性沉积功率密度的最大值则出现在线圈的下方.随着功率的增加,电子密度提高,而电子温度几乎不变,而且功率对于电子密度的空间分布影响很小.随着气压的增加,等离子体的均匀性明显下降,这是因为在较高的气压下,带电粒子与背景气体的碰撞加剧,使得密度分布变得局域.最后,通过对比不同的线圈结构下电子密度的空间分布,表明在较高的气压(20 mTorr)下,使用阵列线圈可以显著优化等离子体的均匀性.综上,本文所提出的三维流体力学模型可以用来指导线圈结构的设计、优化大面积矩形等离子体工艺过程.在下一步的工作中,我们将针对实际的平板显示工艺或光伏工艺中采用的反应性气体放电进行模拟.此外,还可以针对刻蚀工艺,研究偏压效应对离子能量分布的调制行为.