劳动力流动、城市结构匹配与城市生产率

汤小银 吴浩波

摘 要：

新发展格局下，异质性技能劳动力在城市间与城市内的有效配置是影响城市体系分布结构和规模结构均衡的重要因素。基于Behrens等建立的城市模型均衡框架，探讨了实现城市体系分布结构和规模结构均衡时劳动力流动、劳动力技能匹配与城市生产率之间的理论逻辑以及作用机制。在此基础上，使用全国287个地级市2010—2019年的数据，进行了计量检验和异质性分析。结果显示，城市体系分布结构均衡取决于不同技能劳动力的分布结构，城市体系规模结构均衡取决于高技能劳动力的空间集聚、生产力的合理配置和劳动力技能匹配质量，也取决于城市集聚因素与城市成本因素间的权衡。据此提出了优化我国城市体系分布结构、城市体系规模结构以及劳动力市场供给的政策建议：制定城市均衡发展战略，重点关注城市技能劳动力分布结构；继续提高城市规模，尤其是优化大型城市的公共供给；提高中小型城市吸纳异质性技能劳动力的能力；深化劳动力市场改革，提高劳动力供给水平，提高技能匹配质量和效率。

关键词：

异质性劳动力；技能匹配；城市体系分布结构；城市体系规模结构；空间均衡

中图分类号：F249.2

文献标识码：A文章编号：1007-2101（2023）06-0077-10

收稿日期：2023-07-21

基金项目：

东北师范大学哲学社会科学中长期研究重大培育项目“空间经济理论与空间发展研究”（22FR006）；教育部人文社会科学研究规划基金项目“城乡户籍制度与土地制度联动并轨模拟研究”（21YJA790035）；教育部人文社会科学研究青年基金项目“空间经济学视角下特色小镇形成与发展机制的理论研究——以浙江省为例”（17YJC790163）

作者简介：

汤小银（1993-），女，安徽芜湖人，东北师范大学博士研究生；吴浩波（1984-），男，湖南醴陵人，浙江工商大学讲师，博士。

一、引言

城市体系是某一区域范围内不同规模以及不同类型城市组成的巨大空间，其形成源于该空间集聚力和分散力的权衡［1］。城市体系内的不同规模以及不同类型的城市彼此合作相互协调形成均衡的城市体系分布结构，以充分发挥其经济功能，“推动经济实现质的有效提升和量的合理增长”［2］。然而不同城市体系之间或者是同一城市体系内的不同城市为了争夺提高城市生产率所必需的劳动力等要素也会展开激烈竞争［3］，这将打破均衡的城市体系分布结构。那么在这种背景下，是否能存在一个合理的城市体系分布结构呢？这种合理的城市体系分布结构是企业、劳动力等经济主体在保证自由选择的前提下，权衡经济活动聚集效应和拥挤效应而实现的空间均衡状态［4］。在这种空间均衡状态下，所有经济主体都实现效用水平无差异，即所享受的福利水平与承担的城市成本是等价的，所有城市都具有实现福利最大化的人口规模结构和产业结构，从而形成在不同规模以及不同类型城市之间以专业化与分工为基础的城市体系分布结构。

城市体系分布结构的演变因素之一是异质性技能劳动力在不同城市体系之间或者同一城市体系内的不同城市间的有效配置，这揭示了进一步实现合理的城市体系分布结构以提高城市生产率需要提高城市体系承载不同技能劳动力的能力［1，5］。异质性技能劳动力进行区位选择时具有聚集、分类和选择效应。选择效应是指不同技能水平的劳动力会选择流入不同规模和不同类型的城市。Venables等认为异质性技能劳动力和各个城市都存在自选择行为［6］。Rosen-Roback城市空间均衡理论认为，异质性劳动力不同技能水平决定了其所处工作岗位的复杂度，高技能劳动力所处的工作岗位往往更加复杂，从而预期收入也更高。更好的经济机会和更高的预期收入也是异质性劳动力在城市间和城市内迁移的动力，并在权衡生活成本和城市宜居性以后会实现各个城市的均衡［7］。Combes等强调劳动力遷移中的正向与负向选择，正负向选择的判断标准是异质性技能劳动力是否从经济密度低的地区迁往经济密度高的地区［8］。这对应了异质性技能劳动力在城市分布中具有空间非均衡性，经济密度较高的城市往往人力资本分布也较密集［9］。关于分类效应，Behrens等发现，高技能劳动力与城市规模是相互促进的，高技能劳动力一般会迁移到城市规模相对较大的城市发展，而这些城市往往也已经分布着更高生产率的企业和更高技能水平的劳动力［10］。Eeckhout等认为异质性技能劳动力之间存在技能互补，这种互补性会进一步促进分类效应［11］。梁文泉等认为异质性劳动力技能互补的存在可以解释高低技能共同存在城市中的现象，一方面可以体现在知识要素的流动与互补，另一方面也可以体现在专业化分工和功能上的互补［12］。那么何种异质性技能劳动力组合能最大程度地提高总的劳动力生产率，同时保证高技能劳动力在技能互补中也保有一定的获益程度是分类效应要解决的核心问题之一。关于聚集效应，Davis和Dingel基于空间知识经济模型，将城市的聚集力来源假设为异质性城市的学习外部性［13］，即异质性技能劳动力与学习环境相互补充，其聚集伴随着知识与技术的扩散，对提高每个劳动力的生产率水平具有促进作用，从而形成了聚集力。同时不同技能劳动力会进行区位选择，聚集效应也存在着差异，这将进一步促进不同城市在劳动力工资、企业生产率等方面呈现出空间离散现象［14］。

在聚集、分类和选择效应存在的前提下，合理的城市体系规模结构将有助于提高异质性技能劳动力的匹配质量，并引致技能互补水平的提高，这将进一步合理化城市体系分布结构，提高城市生产率。规模相对较大的城市更容易提供复杂性工作岗位［15-16］，高技能劳动力更容易找到复杂性工作，获得更高报酬。同时规模相对较大的城市面临的更高生活成本和更激烈竞争会淘汰技能水平较弱的部分劳动力，形成技能匹配 ［17］，技能匹配意味着将多样化的工作机会合理地分配给异质性技能劳动力或者寻求工作的人员。这种技能匹配与城市体系规模结构密切相关，当城市规模相对较大时，异质性技能劳动力的集聚效应则相对较强，异质性技能劳动力随着城市规模扩大而更加集中，则劳动力市场规模相对越大，存在市场分割的可能性相对较小，异质性技能劳动力的特殊或专用技能水平会更加突出，也越有利于降低企业与异质性技能劳动力间的搜寻成本，更容易获得企业与异质性技能劳动力的更优匹配，从而促进城市就业机会增加和薪资水平的提高，最终导致劳动力工资水平、企业生产率和城市规模间的正向事前关系［18-19］。可见，由于大城市更加多样化的工作机会带来的高水平技能匹配质量，可以使得大城市能更加专注核心业务［20］。然而城市规模过大也会带来城市拥挤效应，不仅会产生过高的城市生活成本，还会导致异质性技能劳动力的空间迁移与匹配障碍，出现异质性技能劳动力供需结构失衡、技能错配等问题，增加了异质性技能劳动力的失业风险。那么是否存在合理的城市体系规模结构呢？城市规模增大会带来工作岗位多样化程度与复杂程度的提高，有助于吸纳异质性技能劳动力，但是城市规模也不能无限制增大，会带来过高的城市生活成本［21］。针对这个问题，Henderson在研究包含生产者和消费者在内的经济体的一般均衡时，提出了城市均衡规模与城市最优规模的概念，两者存在一定差异。城市均衡规模是由劳动者的区位决策和资本所有者的投资决策共同决定的，是最大化自身既有福利水平时的规模，而城市最优规模是指经济体中的每个经济主体都达到潜在福利最大化时的规模［22］。

当前新发展格局下，劳动力在城市间和城市内的流动呈现出新的规律。首先，中小型城市对于农村剩余劳动力的吸纳能力明显下降，并且异质性技能劳动力也不再是仅仅向着北上广深等一线超大城市流动，而是呈现以城市群为导向，逐渐向周边城市迁移的趋势［23］。异质性技能劳动力在流动过程中可能会面临迁移摩擦，从而造成很高的迁移成本［24］，这将进一步重塑城市体系分布结构［25］。其次，城市交通条件的改善、新一代信息技术带来的虚拟经济发展、产业结构重新配置，会使得异质性技能劳动力形成新的转移与流动方向，改变城市体系分布结构［26］。因此，为了在新发展格局下，探讨异质性技能劳动力在城市间和城市内的有效配置，如何影响城市体系分布结构和城市体系规模结构均衡，最终提高城市生产率的问题，本文以Behrens等的城市模型为基础［10］，将城市政府部门和包括高技能、中技能、低技能的异质性劳动力的选择效应、分类效应和匹配质量纳入到模型中，分析实现城市体系分布结构和城市体系规模结构均衡时劳动力流动、劳动力技能匹配与城市生产率之间的作用关系。

二、理论机制与研究假说

（一）基本假设

假设经济系统包括城市经济与农村经济，涉及最终消费品生产部门（M）、中间投入品生产部门（I）和农业部门（A），城市经济由最终消费品生产部门（M）和中间投入品生产部门（I）两部门组成，农村经济由农业部门（A）组成。经济系统里存在大量的异质性劳动力Λ，劳动力异质性主要体现在生产率方面，由工作技能水平t和技能匹配质量m的乘积决定，在其他方面劳动力是同质的。Lc（t）是城市c中技能水平为t的劳动力数量，它是内生决定的，可以由Lc≡∫ttLc（t）dt给出。异质性劳动力消费最终产品的差异化组合和农产品，最终产品的生产使用本地生产的差异化的中间投入品，恒定替代弹性为1+1/ε，其中ε>0。异质性劳动力会在城市和农村间自由流动，可以在不同部门间自由选择就业，选择完成以后则无法自由流动。首先，劳动力会根据自身工作技能选择城市定居，则每种工作技能的累积分布满足ΛGt（t）=∫c0Lc（t）dc，其中t∈［t，t］，C表示适合建为城市的潜在地点集合，C≡［0，c］。为了收入最大化，劳动力在城市定居后会根据自身生产率情况选择成为企业家、工人或者农民。假设技能匹配质量累积分布函数为Gm，城市生产率累积分布为Fc（）。当选择成为工人或者农民时，每个劳动力可以为最终消费品生产部门（M）和农业部门（A）提供a单位的劳动力（a>0）。当选择企业家时，每个劳动力只创立一家企业，投入劳动力生产各种差异化的中间投入品，企业生产率为，则城市总产出Yc为：

Yc=∫Ωc0xc（i）1/（1+ε）di1+ε（1）

其中，xc（i）为城市c生产的第i种中间投入品的产出量，Ωc为城市c生产的中间投入品种类合集。

1.城市一般均衡。

设定位于城市c中的代表性消费者的效用水平满足双重效用函数，第一层效用函数等于把总支出按不同比例支付在农产品和最终消费品组合时的效用。第二层效用函数等于消费者对差异化最终消費品进行消费时的效用。经过整理，位于城市c中的代表性消费者的效用函数可以作如下表述：

MaxUc=MaxCμMC1-μA

CM=∫Ωcxc（i）1/（1+ε）di1+ε（2）

CM，CA分别表示消费者对差异化工业品组合的消费和农产品的消费，市场出清时CM=Yc。进一步构建拉格朗日函数求解：

MaxCM=∫Ωcxc（i）1/（1+ε）di1+ε

s.t.yc=∫Ωcxc（i）pc（i）di（3）

yc为消费者支付土地和通勤费用后的可支配收入，则中间投入品需求xc（i）和价格指数Pc为：

xc（i）=pc（i）Pc-（1+ε）/ε·YcPc

Pc≡∫Ωcpc（i）-1/εdi-ε（4）

pc（i）为城市c生产的第i种中间投入品的价格。由式（4）可以得出中间投入品需求价格弹性为-（1+ε）/ε，当实现企业利润最大化时，每类中间投入品价格等于边际成本的不变加成率加成，即pc（i）=（1+ε）ωcc（i），1c（i），ωc分别为生产单位中间投入品所需的劳动力数量及其工资水平，则可以将式（4）改写为：

xc（i）=c（i）Φc1+1/ε·YcPc

Φc≡∫Ωcc（i）1/εdiε（5）

Φc表示城市c的总生产率水平。ε表示城市集聚经济强度的一种弹性，城市人口规模和城市人口构成都是内生的。企业家利润函数为：

πc（i）=ε1+εpc（i）xc（i）=ε1+εYcc（i）Φc1/ε（6）

由于所有工业品都是当地生产的，城市c的消费者都面临相同的价格指数。不管劳动力生产率水平如何，劳动力都是在比较创建企业后的利润水平πc（i）和成为工人后的收入水平ωcac后进行职业选择。设定Ec、Mc和Ac分别表示在城市c中选择成为企业家、工人和农民的劳动力的劳动生产率水平。假设a<1/ε，求解πc（^）=ωc

^ca可以得到劳动力的劳动生产率临界值^c，则劳动力的劳动生产率水平大于临界值^c时选择成为企业家，劳动生产率水平小于临界值^c时选择成为工人或者农民。由于城市劳动力的劳动力生产率是凸的，所以上述的临界值^c是唯一的：

^c=Φc1+εε×ωcYcε1/（1-aε）（7）

城市c的总劳动力是由所有生产率低于临界值^c的劳动力所供给的，即LSc≡Lc∫^c0acdFc（）。生产率水平高于临界值的劳动力创办的企业（c）对劳动力需求是lc（）=xc（）/c，故城市总劳动力需求是LDc=Lc∫+∞^clc（）dFc（）=［1/（1+ε）］×（Yc/ωc），由劳动力供给等于需求得：

ωcLc∫^c0acdFc（）=Yc1+ε（8）

将价格指数标准化为1，则单个劳动力的工资水平可以写成：

ωc=Φc1+ε（9）

公式（5）中的总生产率水平可以写成：

Φc=Lc∫+∞^c1/εcdFc（c）ε（10）

则均衡时的^c，Φc，ωc，Yc完全可以由式（7）—（10）所表征。进一步结合式（7）、式（8）和式（10）求解^c，可以得到：

^1/ε-ac∫^c0adF（）=1ε∫∞^c1/εdF（）（11）

2.城市最优均衡。

在这里，先把追求城市净产出最大化的政府纳入到模型中。政府的功能是促进城市体系建设，并为每个城市分配劳动力。同时要考虑城市成本，城市总通勤成本为θLγ，在这基础上纳入交通网智能化系数0<ψ<1，ψ越接近于0，则交通网智能化程度越高。城市总通勤成本UC变为：

UC=ψθLγ（12）

进一步，政府作用下各个城市（这里以城市c为例）的目标函数写为：

Max{Tc，Wc，Ac，Ec，Lc（t）}c∈C

∫c∈C［Yc-ψθLγc（t）］dc（13）

其中：

Yc=［∫∈Wc，AcadF（，c）］×

［∫∈E（c）1/εdF（，c）］εL1+εc（14）

f（，c）=∫t∈Tc1tgt，m，c（t，m）dt（15）

Λ=∫c∈CLc（t）dc（16）

Tc为城市c的工作技能水平集合，gt，m，c（t，m）为城市c的工作技能水平t和技能匹配质量m的联合概率密度函数，Lc（t）为城市c的工作技能水平为t的工人数量，f（，c）为城市c的生产力密度分布。

上述方案中的第一个约束条件是城市c的产出，这取决于劳动力分布。第二个约束与劳动力的密度分布有关，与工作技能水平t和技能匹配质量M的联合分布函数有关，其中t取自Tc，密度为gt（t，c），M取自［0，+∞），密度为gm（m）。第三个约束条件是总人口约束。描述上述问题的解决方案相当复杂，因为城市集合和组成以及每個城市的生产率水平都是内生的，我们分步进行。

从a<1/ε开始，政府将具有高生产率水平的劳动力安排为企业家，不具有高生产率水平的人安排为工人或者农民。每个城市都存在生产率水平的临界值^c，

Wc=［0，^c］，Ac=［0，^c］，Ec=（^c，+∞）。在Lc和F（，c）条件下最大化Yc，即：

Max^cYc=［∫^c0adF（，c）］［∫∞^c1/εdF（，c）］εL1+εc（17）

由式（17）的一阶导数等式可以求得这个问题的唯一解是：

^1/ε-ac∫^c0adF（，c）=1ε∫∞^c1/εdF（，c）（18）

城市最优均衡下的式（18）和城市一般均衡下的式（11）相同。由式（11）和（18）可知，如果人口数量L和生产率分布F（·）为给定，那么很容易证明在任意城市1和城市2，F1（）=F2（λ），λ>0时，^2=λ^1。这说明城市生产率水平并不取决于人口数量，而是取决于城市不同技能劳动力的分布比例。由此得到假说1。

假说1：如果存在所有不同规模城市都可以实现福利最大化的城市体系，那么该城市体系的空间均衡取决于不同技能劳动力在不同规模城市之间的分布结构。反过来，如果能够调整不同技能劳动力的空间分布，那么当城市体系实现均衡时，每个城市也实现其福利水平最大化。

（二）城市人口规模

1.城市一般均衡下的人口规模。

回顾≡t·m，在城市c的技能水平为t的劳动力的间接效用函数可以写成：

EVc（t）=∫+∞0Max［ωc·（tcmc）a，π（tcmc）］dGm（m）-ψθLγc

=ωctac［∫^c/tc0macdGm（m）+（tc/^c）

1/ε-a∫+∞^c/tcm1/εcdGm（m）］-ψθLγc（19）

在劳动力技能水平为tc的技能单一型城市中的每个劳动力Lc≡L（tc），通过求解Maxc∈CEVc（t）选择相应城市。进一步定义分配函数μ：T→C，它可以把不同水平劳动技能映射到城市中，城市的选择函数为μ（t）={c∈C：EVc（t）≥EVc′（t），c′∈C}。当均衡时，城市c的技能水平为t的劳动力实现其间接效用最大化：

EVc（t）Lct=tc

dLc+EVc（t）tct=tc

dtc=0（20）

当在技能单一型城市中t=tc时，把式（7）—（10）和式（19）代入式（20）可得：

［（εσ）1+ε（Mctc）1+aLεc-ψθγLγc］

dLcLc+1+a1+ε×

（εσ）1+ε（Mctc）1+aLεc=0（21）

其中，Mc=^c/tc，σ≡∫M0（m/M）adGm（m）=（1/ε）×∫∞M（m/M）1/εdGm（m），

Mc表示企业家技能匹配质量的共同的门槛值，σ表示生产中的单位劳动效率。则式（21）可改写为：

ψγθL（tc）εξt1+ac-L（tc）γ-ε

L（tc）dL（tc）+1+a1+εξtacdtc=0（22）

由此可以求得城市一般均衡下的人口规模：

L^c=（ξt1+ac）1γ-ε

ξ≡（εσ）1+εM1+aψγθ（23）

一方面，一般均衡时的城市人口规模，取决于集聚经济ε、智能化程度ψ和城市成本（θ，γ）之间的权衡，城市人口规模随集聚经济ε、智能化程度ψ的提高而变大，随城市成本（θ，γ）的扩大而变小。另一方面，在一般均衡条件下，城市人口规模的决定性因素是劳动力技能水平t和劳动力技能匹配质量M，城市高技能劳动力越多以及与就业部门的适配度越高，城市人口规模也就越大。

2.城市最优均衡下的人口规模。

先不考虑城市c的区位优势，假设政府通过干预城市c的人口规模，可以实现扣除城市总成本后的城市人均总产出最大化，即：

MaxLc

Yc-ψθLγ+1cLc=A（c）Lεc-ψθLγc

Ac≡∫^c0adF（，c）·

∫∞^c1/εdF（，c）ε（24）

Ac为衡量考虑集聚经济的城市生产率的指标，由式（24）的一阶导数等式可以求得唯一解是：

L^c=

εψγθAc1/（γ-ε）（25）

由式（24）可得，一方面城市最优均衡下的人口规模取决于集聚经济ε、智能化程度ψ和给出的城市成本（θ，γ）之间的权衡，人口规模随集聚经济ε、智能化程度ψ的提高而扩大，随城市成本（θ，γ）的提高而缩小。另一方面，最优均衡下的城市人口规模随城市生产率水平的提高而扩大，而这种生产率水平是由单个劳动力的技能水平所决定，分配到该城市的高技能劳动力越多，城市平均劳动生产率水平越高，城市人口规模也就越大。

通过对一般均衡和最优均衡下的城市人口规模比较发现，这两种不同均衡下的城市体系结构之间存在明显的差异，但推动两者演进的影响因素是相同的，这样就可以得出假说2。

假说2：均衡时城市体系规模结构，一方面取决于城市集聚因素与城市成本因素的权衡，另一方面又取决于高技能劳动力的空间集聚、生产力的合理配置以及劳动力技能匹配质量，高技能劳动力越多，生产力空间布局越合理，不同技能劳动力与就业的匹配程度越高，城市劳动生产率水平也就越高，城市体系规模结构就越合理，承载经济活动和人口的能力就越强。

三、计量模型设定与数据说明

（一）计量模型设定

为了考察影响城市体系结构演变的因素，进行以下三步的计量检验。

首先，检验高、中、低技能劳动力分布对城市生产率的影响，构建如下基准回归模型：

lnF_cityit=β0+β1lnLhit+β2lnLmit+β3lnLlit+β4controlit+dyear+dcity+εit  （26）

其中，F_cityit为城市i在t时期的城市生产率水平，Lhit、Lmit、Llit分別为城市i在t时期的高技能、中技能和低技能劳动力数量，control为城市层面的控制变量，包括政府管理程度和城市化程度。以上变量均进行对数化处理。考虑到时间效应和城市效应的影响，在模型（26）中设置了dyear和dcity两个虚拟变量。

其次，检验高、中、低技能劳动力通过不同技能水平与岗位的匹配程度影响城市生产率的传导机制。为了识别这一传导机制，建立中介效应模型进行检验。以下为递归回归方程：

lnMit=α0+α1lnLhit+α2lnLmit+α3lnLlit+α4controlit+dyear+dcity+εit（27）

lnF_cityit=θ0+θ1lnLhit+θ2lnLmit+θ3lnLlit+θ4lnMit+β4controlit+dyear+dcity+εit（28）

其中，M为中介变量（技能匹配）。中介效应模型检验主要分成三次递归回归，第一次回归是基于计量模型（26），根据其估计出的系数值显著性和正负性来说明劳动力分布是否确实对城市生产率提高具有一定的正向促进作用。第二次回归是基于计量模型（27），根据其估计出的系数值显著性和正负性来说明劳动力与技能匹配之间的确切关系。第三次回归是基于计量模型（28），根据其估计出的系数值显著性和正负性来说明劳动力分布是通过技能匹配的完全中介效应还是部分中介效应影响城市生产率，若系数值不显著，则存在的是完全中介效应，若系数值显著，则存在的是部分中介效用。

最后，检验加入城市集聚经济和城市成本后，劳动力分布对城市生产率的影响，城市集聚经济以城市规模和运输系统智能化程度的交叉项来表征，城市成本以城市拥挤程度来表征，从而设置以下回归方程：

lnF_cityit=κ0+κ1lnLhit+κ2lnLmit+κ3lnLlit+κ4lnMit+κ4controlit+κ5lnNit×Pit+κ6lnUCit+dyear+dcity+εit（29）

其中，Nit为城市i在t时期的城市规模，Pit为城市i在t时期的运输系统智能化程度，UCit为城市i在t时期的城市拥挤程度。

（二）变量说明与数据来源

被解释变量为城市生产率（F_city），采用人均地区生产总值作为代表。核心解释变量包括高、中、低技能劳动力（Lh、Lm、Ll）。选择广泛职业类别对技能水平进行衡量，根据职业所需技能、工作任务的性质以及技术进步对劳动力不同程度的替代作用，对职业进行重新分类衡量技能［27］。第一类，管理人员、科学研究及专业技术人员为高技能劳动力，采用金融业，信息传输、计算机服务和软件业，科学研究、技术服务和地质勘查业，教育业的年末城镇单位从业人员总和作为代表。第二类，办事员及相关文职工作人员、技术工人、机械操作及装配工为中技能劳动力，采用采矿业，制造业，电力、热力、燃气及水生产和供应业，建筑业的年末城镇单位从业人员总和作为代表。第三类，服务业、农林牧渔业以及从事餐饮、保洁、家政等简单体力劳动者为低技能劳动力，采用农、林、牧、渔业，批发和零售业，住宿和餐饮业，租赁和商业服务业的年末城镇单位从业人员总和作为代表。其他解释变量包括：（1）劳动力技能匹配程度（M）。对于劳动力技能匹配程度没有直接的统计数据，考虑到地方财政的教育支出投入可能会带来劳动力技能提升的机会，促使劳动力技能与市场需求更加匹配，所以这里采用地方财政中的教育支出数额作为代表。（2）城市规模（N），采用年末户籍人口作为代表。（3）运输系统智能化程度（P），采用路网密度进行衡量，选择年末实有城市道路面积作为代表。（4）城市成本（UC），选择城市拥挤程度进行衡量，采用城镇登记失业人数作为代表。控制变量包括：（1）政府管理程度（control_Gov），采用地方财政一般支出作为代表。（2）城市化程度（control_UD）。采用城市市政公用设施建设固定资产投资作为代表。所有相关原始数据均来自于《中国城市统计年鉴》，最终整理出包括全国287个地级市2010—2019年的面板数据。

四、计量结果与异质性分析

（一）计量结果分析

1.基准分析结果。

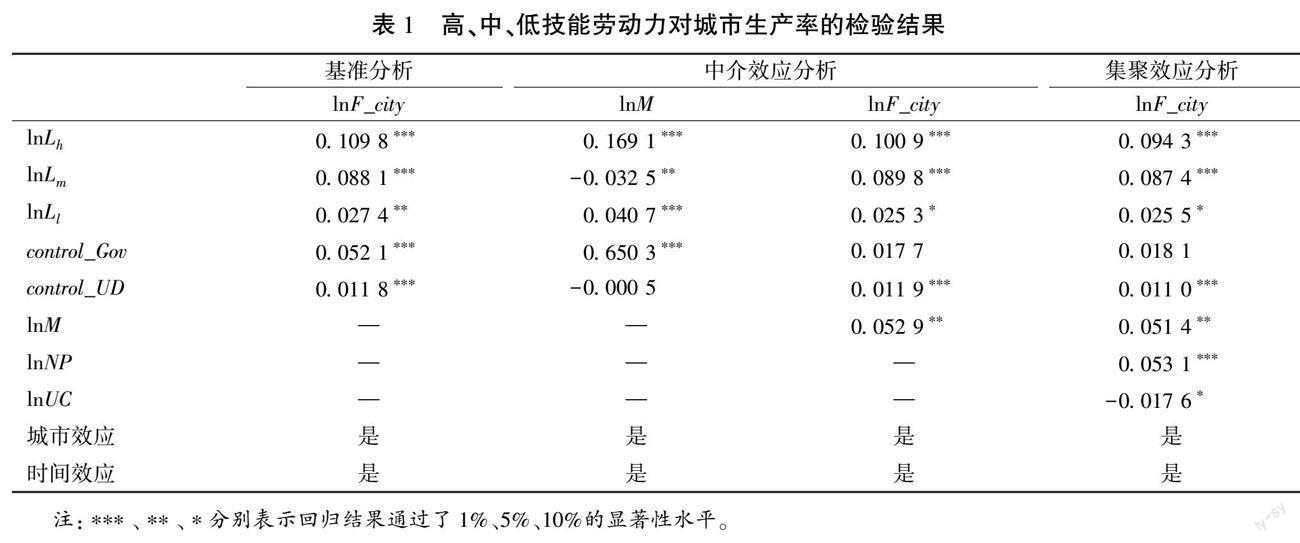
如表1所示，基准分析一栏给出了基于计量模型（26）的估计结果。结果显示高技能、中技能和低技能劳动力都显著促进了城市生产率提高，并且从系数大小来看，高技能劳动力对城市生产率的促进作用是最大的。这验证了假说2中，城市体系发展离不开高技能劳动力的空间集聚，离不开生产力的合理配置。另外，从政府管理程度和城市化程度变量系数的显著性与正负性可知，政府管理程度、城市化程度的提升也促进了城市生产率的提高。异质性技能劳动力的落户决策与各个城市的落户政策、城市教育医疗等基本公共福利水平紧密相关，这将会显著促进异质性技能劳动力在各个城市的配置优化，提高城市生产率。

2.传导机制检验结果。

中介效应分析一栏给出了基于中介效应模型（27）（28）的估计结果，其中第1列是基于计量模型（27）以技能匹配效率为被解释变量的估计结果，结果显示，高技能劳动力和低技能劳动力参数值为显著的正值，中技能劳动力参数值为负值。第2列是基于计量模型（28）以城市生产率为被解释变量的估计结果，结果显示，高、中、低技能劳动力参数值均为显著的正值。相比于第1列的估计结果可以证明，高、中、低技能劳动力通过技能匹配促进城市生产率的提高，传导机制是存在的。这说明技能匹配效率是重要的。随着技能匹配效率的提升，能够降低由于信息不对称形成的异质性劳动力市场搜寻成本，使得异质性技能劳动力在约束条件下实现最优配置，不同技能劳动力能各自投入到生产率最高岗位之中，发挥自身最优的经济价值，提高城市生产率。这验证了假说2中的城市体系发展离不开较高的劳动力技能匹配质量。

3.集聚与拥挤效应检验结果。

集聚效应分析一栏给出了基于计量模型（29）的估计结果，结果显示，城市集聚效应变量系数为显著的正值，城市拥挤效应变量系数为显著的负值。相较于基准分析模型和中介效应模型下的高、中、低技能劳动力参数值，城市集聚效应和城市拥挤效应共同作用下的参数值稍有减小，说明城市生产率受到城市集聚效应和城市拥挤效应的共同影响。经济活动高度集聚提高了岗位—劳动力之间的匹配效率，这样不同技能劳动力都能投入到各自生产率最高的岗位之中，从而提高城市生产率。但是经济活动高度集聚也带来了工作岗位的激烈竞争，造成异质性技能劳动力就业摩擦和失业现象，带来劳动力就业市场风险。最终合理的城市体系规模结构的确定取决于城市集聚效应与城市拥挤效应的权衡。这验证了假说2中的均衡时城市体系规模结构离不开城市集聚因素与城市成本因素间的权衡。

（二）异质性分析检验结果

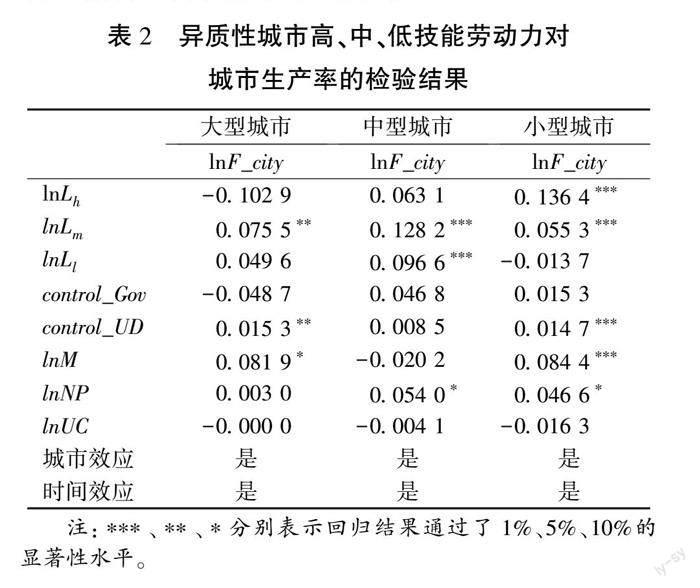
由于城市本身也存在着异质性，为了进一步考察不同规模城市对城市生产率产生的差异化影响，参考魏后凯 ［28］的做法，设定人口（非农业人口）在500万以上的为大型城市、300万～500万人的为中型城市、300万人及以下的为小型城市。表2报告了异质性检验结果。

结果显示，不同类型城市表现出显著差异。在大型城市中，与城市生产率显著相关的变量有中技能劳动力、技能匹配、城市化程度。中技能劳动力与城市生产率呈显著正相关关系，说明中技能劳动力促进城市生产率显著提升。这是因为大型城市提供了更多复杂性工作岗位，从而集聚了大量的高技能劳动力。高技能劳动力吸引了众多高端服务业的聚集，导致异质性技能劳动力逐渐从第二产业进入到第三产业，致使高技能、中技能劳动力的比例失衡，这进一步会影响异质性技能劳动力互补效应和分工效应的发挥。技能匹配与城市生产率呈显著正相关关系，说明异质性技能劳动力匹配质量的提高，城市生产率显著提升。说明大型城市能够更好地发挥劳动力的集聚、选择和分类效应，从而从匹配过程中更大程度地提升城市生产率。城市化程度与城市生产率呈显著正相关关系，说明大型城市能够提供更加丰富的就业岗位、更高的薪资水平和更完善的公共福利水平，保障了一定的就业率，其规模效益能够使得异质性技能劳动力从正外部性中获得收益。

在中型城市中，与城市生产率显著相关的变量有中技能劳动力、低技能劳动力、城市集聚效应。中技能劳动力、低技能劳动力与城市生产率呈显著正相关关系，说明中技能劳动力、低技能劳动力促进城市生产率显著提升。这是因为中型城市长期面临着劳动力大量流失、劳动力结构严重失衡等问题。中技能劳动力和低技能劳动力的回流能够促进异质性技能劳动力在中型城市中的有效配置，从而提升城市生產率。城市集聚效应与城市生产率呈显著正相关关系，说明城市集聚效应的有效发挥能促使城市生产率显著提升。城市集聚效应的有效发挥依赖于基础设施建设逐渐向中型城市的延伸，基础设施建设的完善有利于推动异质性技能劳动力在城市间和城市内的资源配置优化，强化大型城市向中型城市的经济扩散效应，提高中型城市经济发展水平。

在小型城市中，与城市生产率显著相关的变量有高技能劳动力、中技能劳动力、技能匹配和城市集聚效应。高技能劳动力、中技能劳动力与城市生产率呈显著正相关关系，说明高技能劳动力、中技能劳动力促进城市生产率显著提升。说明处于发展停滞或者衰退阶段的小型城市存在与没有高技能劳动力支撑的产业捆绑发展的现象，小型城市发展缺乏高技能劳动力和吸纳高技能劳动力的第三产业，不利于城市生产率的提高。技能匹配与城市生产率呈显著正相关关系，异质性技能劳动力匹配质量的提高，将显著提升城市生产率。小型城市集聚着大量的低技能劳动力，低技能劳动力与小型城市产业结构的匹配，有利于小型城市经济稳定，并可以发展特色经济和专业化经济，在稳步发展中渐进提升。城市集聚效应与城市生产率呈显著正相关关系，同样说明城市集聚效应的有效发挥能促使城市生产率显著提升。

大型城市、中型城市和小型城市的异质性分析结果说明了我国不同城市当前的异质性技能劳动力结构、异质性技能劳动力需求结构存在一定差异，但是理想中不同类型城市所需的异质性劳动力平均技能水平相差无几，均衡分布的城市体系分布结构、城市体系规模结构更有利于增长。这验证了假说1，不同规模城市都实现福利最大化的城市体系，其空间均衡取决于不同技能劳动力在不同规模城市之间的分布结构，反之也成立。

五、结论与启示

本文基于Behrens等建立的城市模型均衡框架，进一步将城市政府部门和包括高技能、中技能、低技能的异质性劳动力的选择、分类效应和匹配质量纳入到模型中，探讨了实现均衡的城市体系分布结构和城市体系规模结构时劳动力流动、劳动力技能匹配与城市生产率之间的逻辑关系以及作用机制。在此基础上，使用全国287个地级市2010—2019年的面板数据，设计了三步计量检验。第一，检验均衡时高、中、低技能勞动力分布对城市生产率的影响；第二，检验均衡时高、中、低技能劳动力分布通过技能匹配影响城市生产率的传导机制；第三，检验均衡时加入城市集聚经济和城市成本后，技能匹配下的劳动力分布对城市生产率的影响。考虑城市异质性，将城市分为大型城市、中型城市和小型城市后分别检验了对城市生产率的影响。结果显示，城市体系分布结构均衡取决于不同技能劳动力的分布结构，即一个经济系统所需的工人/农民与企业家的比例相差无几。城市体系规模结构均衡取决于高技能劳动力的空间集聚、生产力的合理配置和劳动力技能匹配质量，也取决于城市集聚因素与城市成本因素间的权衡。

本文结论对于优化我国城市体系分布结构、城市体系规模结构以及劳动力市场供给具有重要的政策含义。首先，要制定不同规模、不同类型城市均衡发展的战略，重点是关注城市中高技能、中技能和低技能劳动力的分布比例。不同规模、不同类型城市具有不同资源禀赋优势，不应过分追求通过中心城市打造的经济增长极，也不应过分优先发展中小型城市，而是应该充分发挥市场经济规律对于城市发展的引导作用，制度上降低中技能、低技能劳动力在城市的落户门槛，使得异质性技能劳动力能在不同城市中自由流动，提高异质性技能劳动力在城市体系中的配置效率。其次，要继续提高不同规模、不同类型城市的规模，尤其是要优化大型城市的基础设施和公共服务供给。清楚认识大型城市在引领国家经济发展中的重要作用，进一步发挥大型城市在提供就业方面和发展多样化产业等方面的强大实力，通过增加公共建设来提高大型城市的规划与管理能力。同时以城市体系发展战略为发展核心，引导大型城市多样化产业和异质性技能劳动力向周边城市疏散与转移，促进中小型城市规模扩张，提高中小型城市资源承载与配置能力。再次，提高中小型城市的吸纳异质性技能劳动力的能力。中小型城市应以产业和劳动力互为依托、互相促进为发展模式，充分利用当地产业特色、代表性企业发展专业化经济，有针对性地吸引对应技能劳动力就业，在专业化经济稳步发展之后逐渐提高多样化经济发展水平。同时努力完善中小型城市交通基础设施的通达性与公共服务的均等化，保障城市间、城乡间劳动力的正常流动。最后，要深化劳动力市场改革，提高劳动力供给水平，提高技能匹配质量和效率。各城市应该从自身实际情况出发，采取手段降低劳动力迁移成本和劳动力市场分割程度。同时深化教育培训制度改革，提供差异化的专业知识和技能水平方面的培训，提高异质性技能劳动力对岗位需求的适配程度。

参考文献：

［1］安虎森.城市经济学的一些理论问题［J］.河北经贸大学学报，2022（4）：54-64.

［2］习近平.高举中国特色社会主义伟大旗帜为全面建设社会主义现代化国家团结奋斗——在中国共产党

第二十次全国代表大会上的报告［M］.北京：人民出版社，2022：28-29.

［3］何文.人口规模、交易成本和城乡空间经济——基于新经济地理学城市体系模型的理论研究［J］.河北经

贸大学学报，2022（5）：57-63.

［4］陆铭，向宽虎，陈钊.中国的城市化和城市体系调整：基于文献的评论［J］.世界经济，2011（6）：3-25.

［5］安虎森.提升城市群功能的现实必要性及实践路径［J］.人民论坛，2021（24）：62-65.

［6］VENABLES A J.Productivity in cities： self-selection and sorting［J］.Economics， 2010， 11（2）：241-251.

［7］COSTINOT A，VOGEL J.Matching and Inequality in the World Economy［J］.Journal of Political Economy， 2010，118（4）：747-786.

［8］COMBES P，DURANTON G，GOBILLON L，et al.The productivity advantages of large cities： Distinguish agglomeration from firm selection［J］.Econometrica，2012，80（6）：2543-2594.

［9］李海峥，贾娜，张晓蓓，等.中国人力资本的区域分布及发展动态［J］.经济研究，2013（7）：49-62.

［10］BEHRENS K，DURANTON G，ROBERT-NICOUD F.Productive Cities：Sorting，Selection，and Agglomeration［J］.Journal of Political Economy，2014，122（3）：507-553.

［11］EECKHOUT J，PINHEIRO R，SCHMIDHEINY K.Spatial Sorting［J］.Journal of Political Economy，2014，122（3）：554-620.

［12］梁文泉，陆铭.城市人力资本的分化：探索不同技能劳动者的互补和空间集聚［J］.经济社会体制比较，2015（3）：185-197.

［13］DAVIS D R，DINGEL J I.Spatial Knowledge Economy［J］.American Economic Review，2019，9（1）：153-170.

［14］陆铭，高虹，佐藤宏.城市规模与包容性就业［J］.中国社会科学，2012（10）：47-66+206.

［15］ELVERY J A.City Size and Skill Intensity［J］.Regional Science and Urban Economics，2010，40（6）：367-379.

［16］KOSTER H，OZGEN C.Cities and Tasks［J］.Journal of Urban Economics，2021，126（6）：1-44.

［17］张军涛，翟婧彤，贾宾.城市规模与人力资本技能溢价：集聚效应和选择效应［J］.统计研究， 2021（2）：73-86.

［18］KIM S.Labor specialization and the extent of the market［J］.Journal of Political Economy，1989，97（3）：692-705.

［19］MION G，Naticchioni P.The spatial sorting and matching of skills and firms［J］.Canadian Journal of Economics，2009，42（1）：28-55.

［20］KOK S.Town and City Jobs：How Your Job is Different in Another Location［J］.Regional Science and Urban Economics，2014，49：58-67.

［21］HENDERSON J V， Thisse J F.Handbook of Regional and Urban Economics，Volume 4：Cities and Geography［M］.Amsterdam：Elsevier，2004：2119-2171.

［22］HENDERSON J V.The sizes and types of cities［J］.The American Economic Review，1974，64（4）：640-656.

［23］孫晓华，郭旭，范世龙.社会网络、技能提升与就业地选择［J］.经济研究，2023（5）：116-134.

［24］TOMBE T，ZHU X.Trade，Migration，and Productivity：A Quantitative Analysis of China［J］.American Economic

Review，2019，109（5）：1843-1872.

［25］BEHRENS K，MION G，MURATA Y，et al.Spatial frictions［J］.Journal of Urban Economics，2017，97：40-70.

［26］郑腾飞，柯善咨.交通条件、城市规模和劳动技能匹配效应［J］.财经研究，2019（11）：4-19.

［27］ACEMOGLU D，AUTOR D.Skills，Tasks and Tehnologies：Implications for Employment and Earnings［R］.NBER Working Paper，2010，No 16082.

［28］魏后凯.中国城镇化进程中两极化倾向于规模格局重构［J］.中国工业经济，2014（3）：18-30.

责任编辑：彭 青

Labor Mobility， Urban Structure Matching and Urban Productivity

——Taking the "Second

Tang Xiaoyin1， Wu Haobo2

（1.School of Geographical Sciences， Northeast Normal University， Changchun Jilin 130024， China;

2.School of Economics， Zhejiang Gongshang University， Hangzhou Zhejiang 310018， China）

Abstract：

Under the new development pattern， the effective allocation of heterogeneous skilled labor between and within cities is an important reason affecting the equilibrium of the distribution structure and the scale structure of the urban system. Based on the city model equilibrium framework established by Behrens et al， this paper explores the theoretical logic and the mechanism of action between labor mobility， labor skill matching and urban productivity when realizing the equilibrium of the distribution structure and the scale structure of the urban system. On this basis， econometric tests and heterogeneity analyses are conducted using data from 287 prefecture-level cities in China from 2010 to 2019. The results show that the equilibrium of the distribution structure of the urban system depends on the distribution structure of the labor force with different skills， and the equilibrium of the scale structure of the urban system depends on the spatial agglomeration of the highly skilled labor force， the rational allocation of productivity and the quality of labor force skill matching， as well as depends on the trade-off between the urban agglomeration factor and the urban cost factor. Accordingly， policy recommendations for optimizing the distribution structure of  urban system， the scale structure of the urban system， and the supply of the labor market in China are put forward： firstly， a strategy for balanced urban development should be formulated， focusing on the distribution structure of the skilled labor force in the cities; secondly， continue to improve the scale of cities， especially optimizing the public supply of large cities; thirdly， improve the ability of small and medium-sized cities to absorb heterogeneous skilled labors; finally， deepen the labor market reforms to raise the level of labor supply and improve the quality and efficiency of skills matching.

Key words：

heterogeneous labor force; skill matching， distribution structure of the urban system; scale structure of the urban system; spatial equilibrium