改进希尔伯特-黄变换含噪振动信号时频分析

孙 苗, 杨钧凯, 吴 立

(1. 湖北国土资源职业学院 环境与工程学院,武汉 430090; 2. 武汉华中科大建筑规划设计研究院有限公司,武汉 430070; 3. 中国地质大学(武汉) 岩土钻掘与防护教育部工程研究中心,武汉 430074; 4. 中国地质大学(武汉) 工程学院, 武汉 430074)

自然界中绝大部分信号都是非线性、非稳态信号,振动信号属于此类,是典型的复杂多分量信号[1-3],希尔伯特-黄变换(Hilbert-Huang Transform, HHT)[4]具有的自适应性使其很适合振动信号时频分析[5-6].通过时频分析,可实现对以时域形式呈现的信号进行“翻译”,使其展现更多的隐藏信息.以此帮助相关工作人员研究振动信号产生的时频能量,是否会引起受迫振动结构产生不良反应[7-9].

HHT由经验模态分解(Empirical Mode Decomposition, EMD)和Hilbert变换组成.振动信号监测过程中不可避免会因测试仪器、监测环境等因素而导致实际测得的信号中混有噪声.噪声的混入使得EMD得到的固有模态函数(Intrinsic Mode Function, IMF)具有严重的模态混淆[10-11],而传统Hilbert变换受Bedrosian定理的约束在处理此类IMF分量会得到负值瞬时频率,导致实测振动信号的时频特征难以识别,或者识别结果缺乏准确性[12-13].

基于此,提出CEEMDAN·MPE-INHT时频分析算法,该算法实现分两步.第1步抑制噪声干扰,对EMD进行双重改进,为控制低频噪声改进EMD得到自适应补充集合经验模态分解(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise,CEEMDAN),为控制高频噪声引入多尺度排列熵(Multiscale Permutation Entropy, MPE),即通过CEEMDAN·MPE控制噪声干扰.第2步排除Bedrosian定理的限制,优化Hilbert变换,得到改进归一化Hilbert变换(Improved Normalized Hilbert Transform, INHT).

首先,通过混有噪声的仿真振动信号验证该算法不仅可有效抑制EMD固有的模态混淆现象,同时得到具有实际物理意义的瞬时频率.再将该算法用于实际工程获得的含噪振动信号时频分析中,发现该算法得到的时频谱在时域和频域均具有较高的分辨率,可有效提取振动信号时频能特征参数,提高了时频分析参数提取精度,对振动信号危害控制具有一定的指导作用.

1 CEEMDAN·MPE-INHT时频分析算法

1.1 CEEMDAN

CEEMDAN[14]是在分解的每一阶段添加有限次自适应白噪声,实现在减少分解次数的同时减小重构误差.通过算法原理分析,发现CEEMDAN对监测中混入低频噪声的控制源于所添加自适应白噪声的抵消能力.

1.2 MPE

MPE[15]相比排列熵(Permutation Entropy, PE)[16]的优势在于多尺度粗粒化处理,这一处理是将时间序列(本文时间序列为CEEMDAN得到的IMF)进行分段并在各段进行平均化,进一步提高处理精度.再通过设置排列熵阈值,控制处理后时间序列的熵值,进而实现抑制振动信号在监测中混入的高频噪声.

1.3 改进归一化Hilbert变换

传统的Hilbert变换受Bedrosian定理的约束,在处理非平稳、多分量信号时会得到负值瞬时频率.针对此现象,Huang等[17]提出归一化希尔伯特-黄变换(Normalized Hilbert Transform, NHT),以此来提高瞬时频率的计算精度.本文在NHT的基础上做出了改进,Huang等[17]用于NHT的IMF来自于EMD或集合经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)[18-19],但EMD和EEMD在进行含噪信号分解时不可避免会产生模态混淆的问题.而本文IMF由CEEMDAN·MPE得到,对IMF模态混淆进行了抑制.对此类IMF进行NHT,便可实现改进归一化Hilbert变换(INHT).INHT的操作和NHT十分相似,区别在于,NHT所用的IMF来源是EMD或EEMD,而INHT使用的IMF来自于CEEMDAN·MPE,因此这里不加累述,具体可参考文献[17],将其中的IMF替换成CEEMDAN·MPE得到的IMF即可实现INHT.

1.4 CEEMDAN·MPE-INHT时频分析算法流程图解

CEEMDAN·MPE-INHT算法的建立思路是对含噪振动信号时频分析时遇到影响其精度的问题进行逐一改进,前述1.1节～1.3节简单说明了组成CEEMDAN·MPE-INHT的每一部分单独算法的运行原理,并未详细展开,为增加论文的可读性,将CEEMDAN·MPE-INHT时频分析算法的运算流程图进行展示,如图1所示.

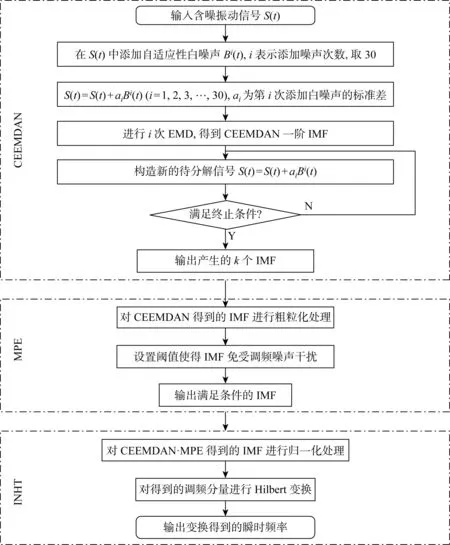
图1 CEEMDAN·MPE-INHT时频分析算法流程图Fig.1 Flow chart of CEEMDAN·MPE-INHT time-frequency analysis algorithm

2 仿真信号CEEMDAN·MPE-INHT时频分析

2.1 仿真信号的建立

构建含有噪声的仿真振动信号,噪声的添加是为了模拟在实际振动信号监测时混入的噪声.仿真信号波形图如图2所示.仿真信号S(t)=x1(t)+x2(t),x1(t)=wgn(1,N, 0.1),即功率为0.1的噪声信号,N为采样点数,如图2(a)所示;x2(t)=sin(2π×50t),即频率f=50 Hz的正弦信号,如图2(b)所示;仿真信号如图2(c)所示.采样点数N=512,采样时间t=1.0 s.

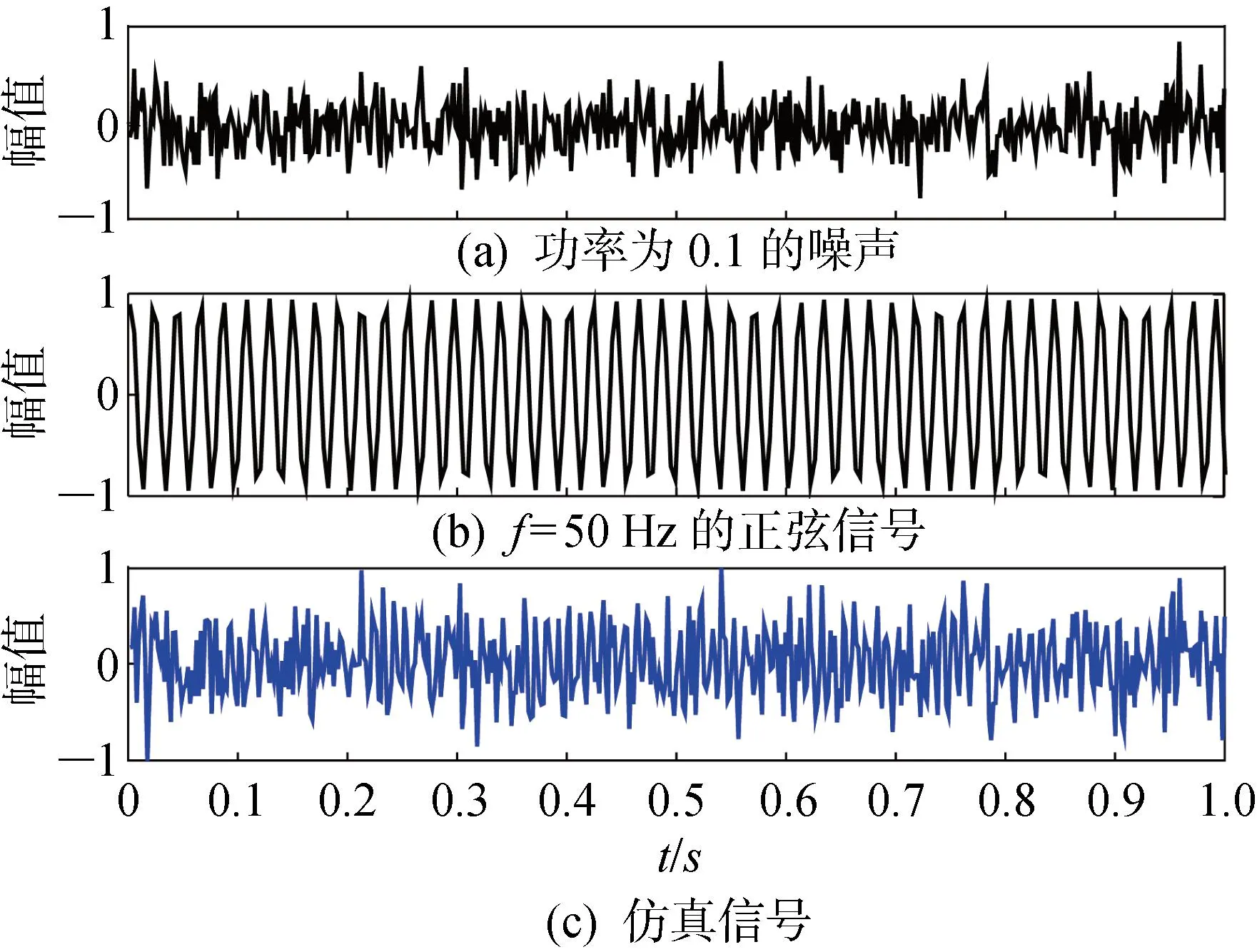
图2 仿真信号波形图Fig.2 Waveform of simulation signal

2.2 仿真信号模态分解

为突出CEEMDAN·MPE对EMD模态混淆的抑制作用,分别采用EMD、EEMD、CEEMDAN和CEEMDAN·MPE对S(t)进行模态分解,分解结果如图3所示.图中:IMF为不同模态分解方法得到的固有模态函数;R为不同模态分解方法得到的余项.图3(a)为EMD结果,不难发现IMF1是难以除去的噪声信号;IMF高频模态混淆严重,如IMF2在t=0.24,0.42,0.54,0.80 s附近都出现高频向中频发展的现象;中频模态混淆有所缓解,如IMF3在t=0.42 s及右端点附近存在向低频发展的趋势;低频相对稳定,如IMF6.图3(b)为EEMD结果,高频IMF模态混淆相比EMD有所缓解,但依旧存在,如IMF1在t=0.42 s处向中频发展;中频相对稳定,如IMF4和IMF5;低频出现模态分裂[17],该现象是模态混淆的第2种现象,即相同的模态分量出现在不同的固有模态函数中,如IMF7和IMF8.图3(c)为CEEMDAN结果,低频分布稳定,高频IMF1出现了模态混淆,出现在t=0.42,0.64 s附近;图3(d)为CEEMDAN·MPE结果,分解得到的IMF从高频向低频依次排列,未见明显模态混淆现象.

图3 仿真信号经不同方法的分解结果Fig.3 Results of decomposition of simulation signals by different methods

2.3 仿真信号Hilbert变换和INHT对比分析

为验证CEEMDAN·MPE-INHT含噪振动信号时频分析的准确性,依据图3不同模态分解方法所得IMF结果,分别进行EMD-HT、EEMDNHT、CEEMDAN-INHT和CEEMDAN·MPEINHT,得到的变换结果即时频谱如图4所示.图中:E为能量谱密度.

图4 仿真信号时频谱图Fig.4 Time-frequency spectrum of simulated signals

图4(a)为EMD-HT时频谱,可发现时频谱出现了50 Hz以上的虚假分量,该分量较发散,难以识别,时频谱在时间和频率这两个维度的分辨率都不高.图4(b)为EEMD-HT时频谱,可发现50 Hz以上的虚假分量相比EMD-HT少,频率分辨率有所提高.图4(c)为CEEMDAN-INHT得到的时频谱图,基本未见低频模态混淆,50 Hz以下时频谱频率分辨率高,但是在t=0.12,0.36,0.80 s附近出现了高频噪声干扰导致频率分辨率降低.对比图4(a)、图4(b)和图4(c)时频谱在高频和低频处的分辨率,可以发现CEEMDAN相比EMD和EEMD,对低频噪声具有很好的抑制作用,但对高频噪声缺乏控制力度.图4(d)所示为CEEMDAN·MPE-INHT得到的时频谱图,该时频谱在时间和频率维度均具有较高分辨率,未见高频和低频模态混淆.再次表明CEEMDAN对噪声信号引起的低频模态混淆具有良好的抑制作用,MPE也能有效控制噪声信号引起的高频模态混淆,同时CEEMDAN·MPE得到的IMF经过INHT能够得到具有实际物理意义的时频信息,即CEEMDAN·MPE-INHT时频分析算法不仅可有效抑制噪声信号引起的EMD模态混淆,同时得到时频分辨率双高的信号频谱图.

3 基于 CEEMDAN·MPE-INHT 的含噪振动信号时频分析

振动信号在自然界分布极广,本文实际应用中,以含噪爆破地震波振动信号作为研究对象,重点研究CEEMDAN·MPE-INHT算法的实际含噪振动信号时频分析.

为满足交通运输需求,将福建某原有双向四车道隧道原位扩建为双向八车道隧道,相关设计参数如表1所示.施工要求右侧隧道在封闭施工过程中左侧隧道依然保持正常通车状态,因此,在右侧隧道进行爆破施工时,有必要对左侧通车隧道进行动态跟踪监测.

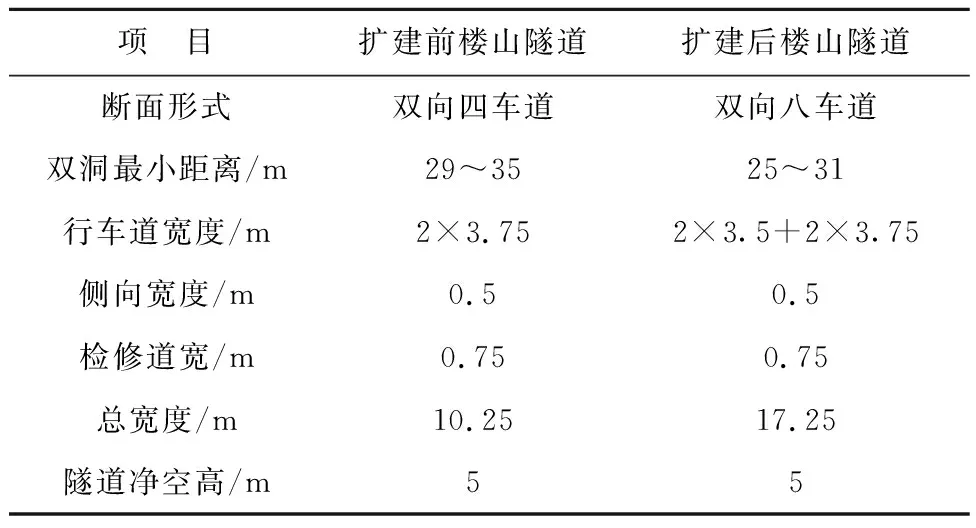
表1 隧道扩建前后设计参数Tab.1 Design parameters before and after tunnel expansion

采用UBOX-5016爆破振动智能监测仪对左侧通车隧道进行监测,选取监测点中一条典型爆破振动信号作为研究对象,如图5所示.图中:v为速度;采样时间t=1.0 s;采样点为 1 500.

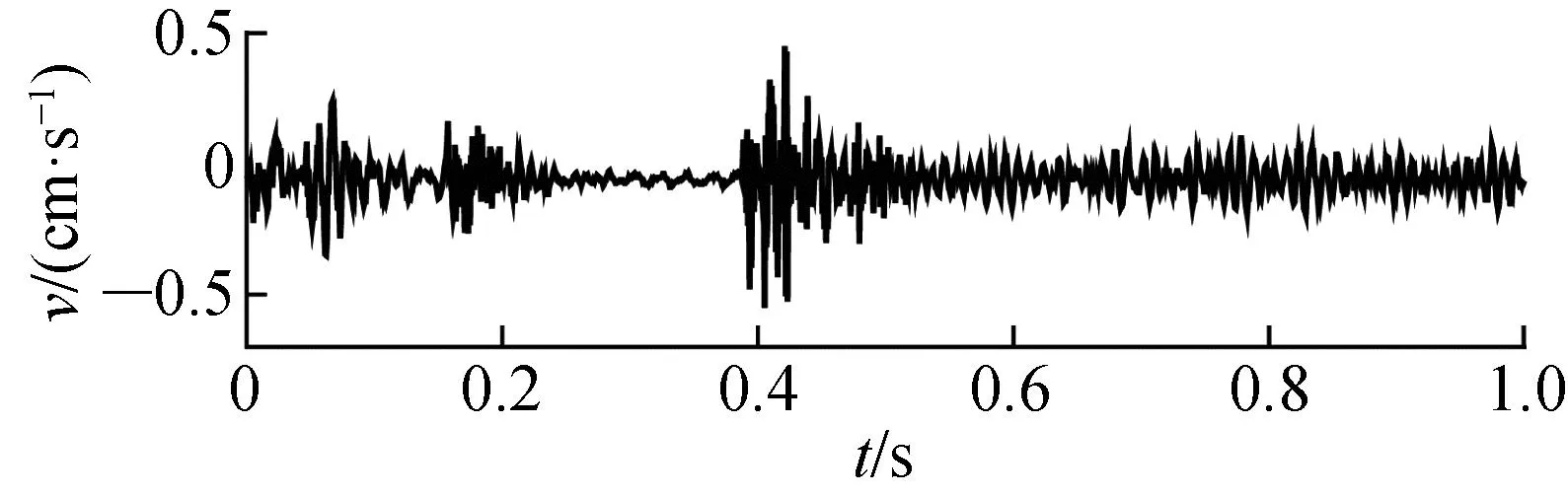
图5 实际爆破地震波监测信号波形图Fig.5 The waveform of the actual blasting seismic wave monitoring signal

对图5所示的爆破地震波监测信号进行基于CEEMDAN·MPE-INHT的时频分析,分析结果如图6～图13所示.图6～图13中的(a)图是图5信号经CEEMDAN·MPE得到的IMF;(b)图是每个IMF对应的边际谱;(c)图是每个IMF的时频谱图,这里忽略了余项R.

图6 IMF1时频能量特征图Fig.6 Time-frequency energy characteristic of IMF1

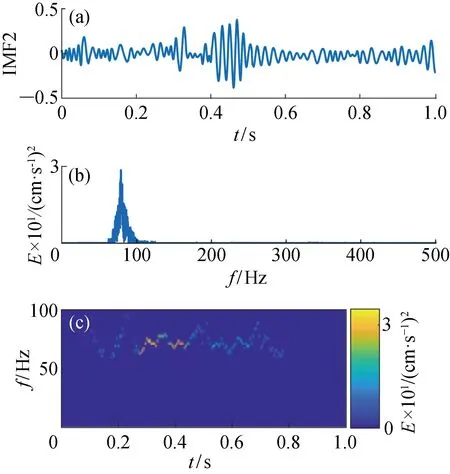
图7 IMF2时频能量特征图Fig.7 Time-frequency energy characteristic of IMF2

图8 IMF3时频能量特征图Fig.8 Time-frequency energy characteristic of IMF3

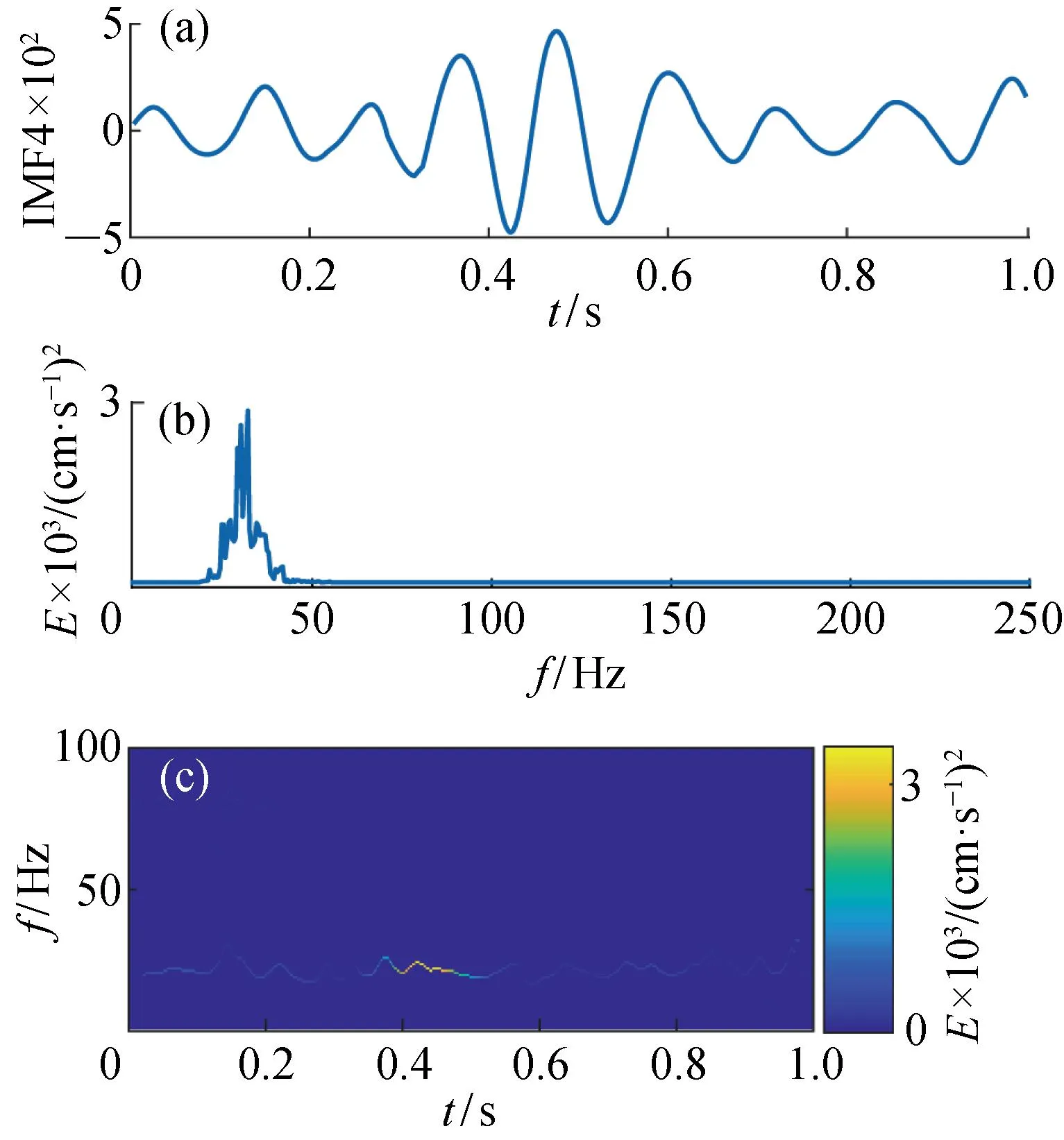
图9 IMF4时频能量特征图Fig.9 Time-frequency energy characteristic of IMF4

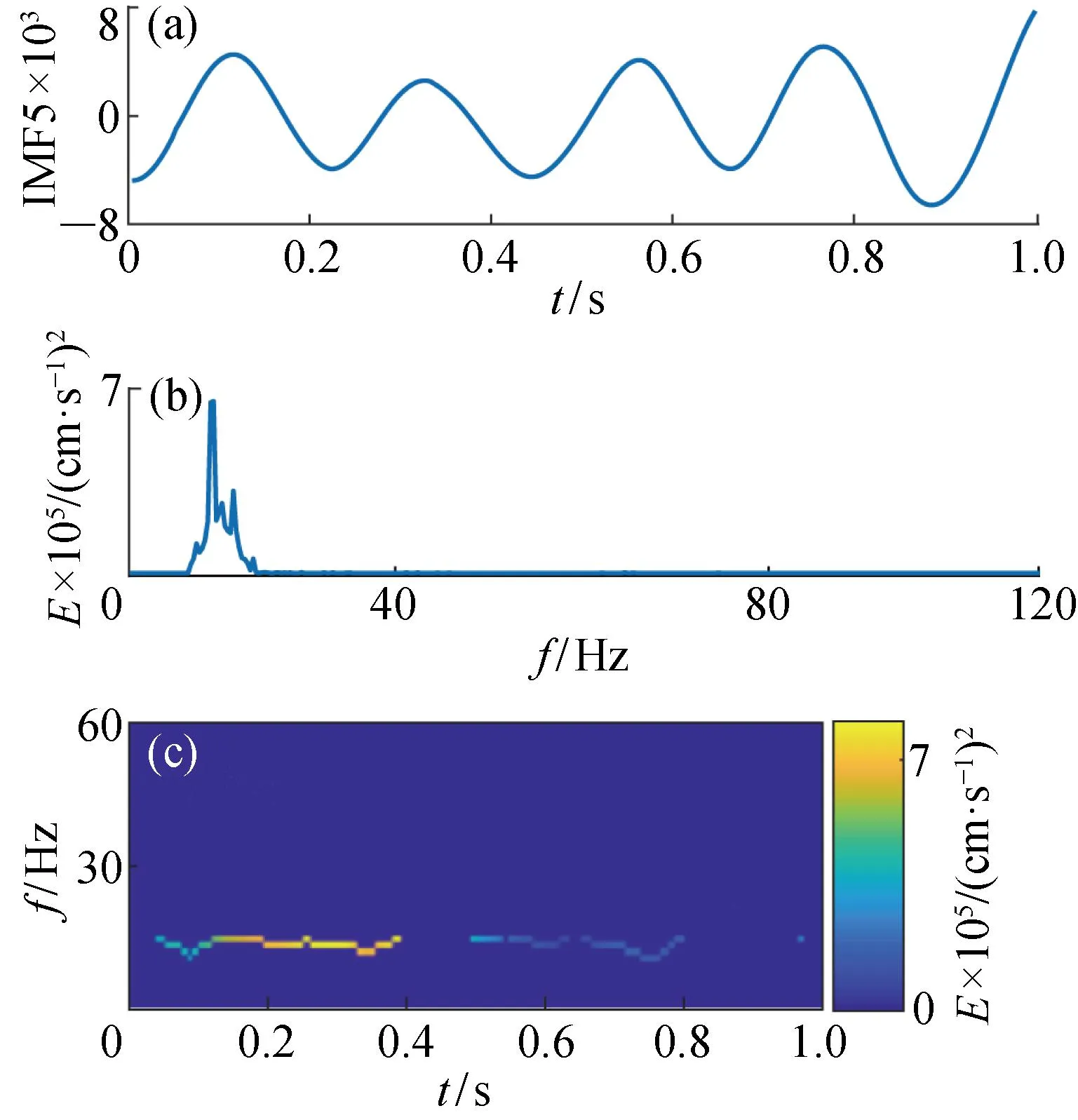
图10 IMF5时频能量特征图Fig.10 Time-frequency energy characteristic of IMF5

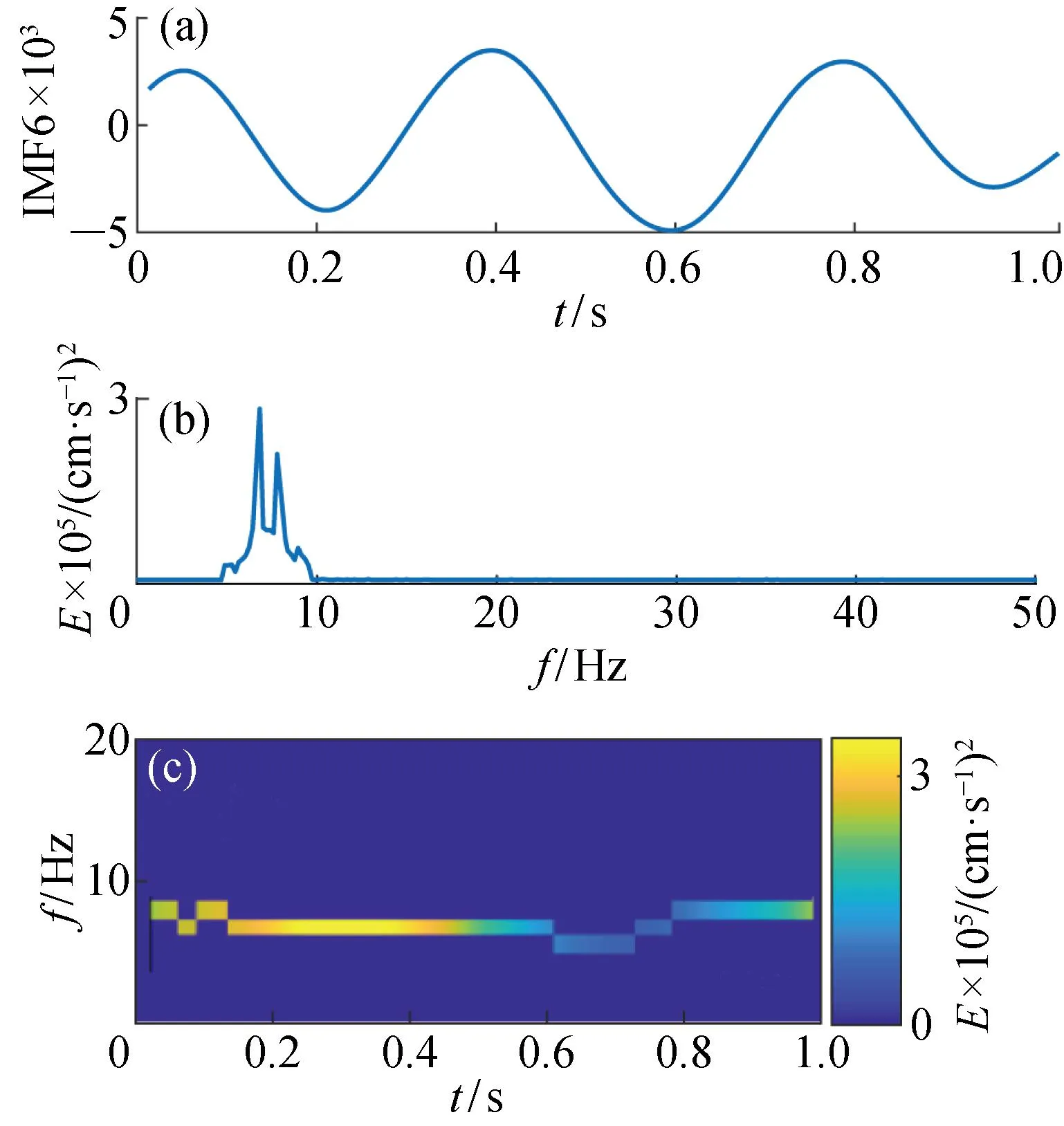
图11 IMF6时频能量特征图Fig.11 Time-frequency energy characteristic of IMF6

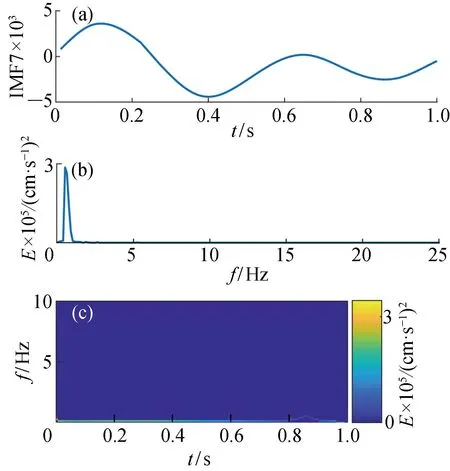
图12 IMF7时频能量特征图Fig.12 Time-frequency energy characteristic of IMF7

图13 IMF8时频能量特征图Fig.13 Time-frequency energy characteristic of IMF8

观察图6～图13的(a)图可发现,图5信号经CEEMDAN·MPE得到了8个IMF分量,IMF从高频到低频依次排列,每个IMF分量都比较稳定,未见明显的模态混淆.

观察图6～图13可发现,基于CEEMDAN·MPE-INHT时频分析算法得到的时频谱图在时域和频域都拥有很高的分辨率.其中IMF1频率范围为100～300 Hz,持续时间0.00～1.00 s;IMF2频率范围为60～100 Hz,持续时间0.10～0.80 s;IMF3频率范围为40～60 Hz,持续时间0.00～0.80 s;IMF4频率范围为20～40 Hz,持续时间0.00～1.00 s;IMF5频率范围为10～20 Hz,持续时间0.08～0.80 s;IMF6频率范围为5～10 Hz,持续时间0.00～1.00 s;IMF7和IMF8频率最低,主要在0～5 Hz,持续时间0.00～1.00 s.通过分析图6～图13可发现,信号能量主要集中在IMF1和IMF2中,其次在IMF3和IMF4中,地震波信号频率主要分布在100～300 Hz,能量也主要集中在高频.

进一步分析得到图5中的信号的三维时间-频率-能量谱图,如图14所示.观察图14,可发现图5含噪振动信号的主频是110.5 Hz,爆破地震波信号能量也主要集中在100 Hz以上的频率部分,该结果和单个IMF时频能量特征图时频能量信息分布一致.现有研究表明[20-21],地下工程中既有隧道的固有频率在50 Hz左右,结合本次爆破地震波信号时频图和三维时间-频率-能量分布情况,可以初步判断本工程分离式隧道一侧隧道扩挖爆破产生的地震波信号不会引起另一侧隧道的共振.

图14 爆破地震波监测信号时间-频率-能量三维图Fig.14 Time-frequency-energy three-dimensional diagram of blasting seismic wave monitoring signal

综上所述,基于CEEMDAN·MPE-INHT的含噪振动信号时频分析算法,不仅有助于抑制含噪监测信号引起传统EMD固有的模态混淆现象,同时CEEMDAN·MPE得到的IMF经INHT得到的时频图和三维时频能量图可清晰展示振动信号内在所蕴含的频率-能量之间的对应关系,即得到的时频信息具有清晰的物理意义.对含噪振动信号特征参数提取、振动危害控制及科学制定防护措施具有重要的意义.

4 结论

(1) 通过CEEMDAN·MPE-INHT算法在含噪仿真振动信号和实际含噪振动信号时频分析中的应用,验证了该算法可抑制EMD固有的模态混淆现象,并得到时频分辨率均高的时频谱图,谱图对应的时频参数实际物理意义明确.

(2) INHT得到的瞬时频率为IMF的调频分量Hilbert变换得到的,使得传统的Hilbert变换免受Bedrosian定理的限制,因此INHT相比Hilbert变换得到的瞬时频率真实性更高.

(3) 基于CEEMDAN·MPE-INHT含噪振动信号时频分析算法,可得出含噪振动信号内在所蕴含的时间-频率-能量之间的对应关系,该对应关系有助于含噪振动信号内在特征的识别和实际工程振动危害控制.