冲刷防护作业中流态固化土对海洋桩基作用力的数值研究

李濡宇, 毋晓妮, 陈锦剑, 蒋海里, 王会丽

(1. 上海交通大学 海洋工程国家重点实验室,上海 200240;2. 上海公路桥梁(集团)有限公司,上海 200433)

在国家 “海洋强国”战略实施下,我国正加快对海上空间的开发利用.跨海大桥、海上风力发电和海洋油气平台工程项目日益增多[1].这些工程大多采用桩基础.海洋桩基受到波浪和海流的作用,其周围水动力条件发生改变后会打破桩基周围海床泥沙平衡,容易发生局部冲刷,导致桩基承载力弱化,而发生结构倾覆等工程安全问题.统计资料表明,冲刷是海洋工程事故的重要原因[2].为了确保工程的安全和稳定运行,有必要对海洋结构的桩基础进行局部冲刷防护.

2019年,国家电投集团江苏海上风力发电有限公司在江苏如东大丰风电场首次采用固化土方案进行桩基防冲刷工程实践探索[3-4].该技术对淤泥进行固化处理,利用流态固化土初期的流动性,将其泵送至桩基周围海床表面或者发展中的冲刷坑中,随着时间推移,流态固化土逐渐硬化成型,形成防护层,可起到冲刷防护和修复的效果[5].连续两年的现场监测结果表明,固化土方案能有效控制桩基础局部冲刷,是一种有效且具备广阔应用前景的防冲刷新技术.然而,在施工过程中,泵送流态固化土会对承载力弱化的桩基础产生作用力,该作用力的量级大小以及是否会影响既有工程的安全,犹未可知.因此,研究泵送过程中流态固化土对海洋桩基的作用具有重要的科学意义和工程应用价值.

初始状态的高含水率固化土是一种流态化的泥浆,属于非牛顿流体范畴[6].目前仍未有针对泵送过程中固化土对桩基作用力的相关研究.但针对类似的非牛顿流体对结构作用力的研究,现有研究中多为陆上泥石流和海洋滑坡等类似泥浆流对桩基、桥墩以及管线的作用.王友彪[7]通过试验和数值手段研究了陆上泥石流对桥墩的冲击力,提出了冲击力三层模型.Zakeri等[8-9]通过试验和数值手段研究了海底滑坡对管线的冲击作用,得出了管道拖曳力经验公式.冯斌等[10]和Li等[11]分别开展了海底滑坡对海洋桩基作用力的试验和数值分析,对作用力的影响因素进行了探讨.Randolph等[12]提出了海底滑坡对管线作用力的土力学分析思路,给出轴向和法向承载系数计算公式以及管道的破坏包络面.王立忠等[13]通过试验对近海慢速滑动泥流对管线作用进行研究,得到了管道受力的一般规律.以上现有研究为本研究提供了可靠的研究思路,即采用两相流技术对流态固化土对桩基的作用力进行研究.

考虑到泵送施工的流态固化土对桩基可能造成的不良影响,本文基于东海大桥海上风电场固化土冲刷防护项目背景,参考相关水文地质资料,建立数值模型,分析了流态固化土对桩基作用力的影响规律,提出了作用力简化分析思路,并给出了流态固化土对桩基作用力的简易评估公式.研究结果可为固化土防冲刷技术的工程应用提供控制依据.

1 理论基础

1.1 基本假设

目前,固化土防冲刷技术于东海大桥附近风电场有初步应用探索.实际工程中,整个流态固化土浆液在泵送过程处于复杂多变的海洋环境,存在诸多不确定性,有必要对模型进行简化.

(1) 一般地,常选平潮期分批次施工,波浪作用可忽略不计.各批次施工周期相较于潮流变化周期较短,且潮流随深度变化较小,因此可简化为恒定水流环境.

(2) 桩基础刚性较大,位移及振动可忽略,可视为刚性体插入海床.恒定流作用下泵浆管位移影响忽略,视为竖直向下的固定刚体.

(3) 实际的冲刷坑形状复杂、不规则.为方便分析,根据文献[14],采用概化的倒圆台形冲刷坑模型.

1.2 两相流模型

实际工程中,常对工程废弃土、海洋滩涂、疏浚淤泥等泥状物进行固化处理和泵送施工,实现泥状物的资源化利用.从泥源土特性来讲,这些原料土多为淤泥质黏土,为保证流动性要求,原料土初始含水率通常需调配至80%～135%(2.5～3.5倍液限),因此,高含水率流态固化土为泥浆状材料,可看成一种具有黏滞性的非牛顿流体.在防冲刷应用场景中,高含水率流态固化土泵入桩基周围冲刷坑中,其运动过程可视作泥浆在水中流动,而非土体滑动,可以用两相流理论进行分析[15].

高含水率流态固化土在水中流动扩散,浆水交界面会有掺混,因此采用欧拉两相流模型模拟高含水率流态固化土在水中流动过程.其控制方程包括连续性方程和动量方程.多相流连续性方程如下:

(1)

式中:αq、ρq和Uq分别为第q相的体积分数、密度和速度;t为时间.多相体积分数满足下式:

(2)

式中:n为流体相数.

动量方程由Navier-Stokes描述,表达式如下:

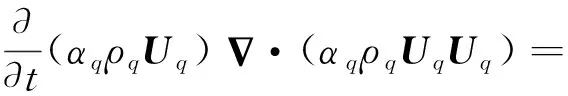
Fq+Flift,q+FVm,q+Ftd,q

(3)

(4)

(5)

Kpq为相间动量交换系数.

2 数值模型建立与验证

通过ANSYS Fluent建立考虑水流和流态固化土的欧拉两相流数值模型,对桩基础周围冲刷坑内流态固化土泵送过程进行模拟.初始状态,计算域充满恒定流速的动水以模拟恒定水流环境,流态固化土从泵浆管口泵入,并对桩基础产生作用力,分析泵速、海流流速、固化土类型等因素对桩基所受作用力的影响.

2.1 计算域和边界条件

本研究的重点区域为水面以下部分,因此仅建立水面以下模型,计算模型如图1所示.桩径D设置为5 m.计算域长宽为18D×14D,水深Hw取10 m.本模型的冲刷坑深度h取6 m[14-16],冲刷坑顶部宽度为2h[16].泵浆管径d取 200 mm,H为水下部分泵浆管长,W为泵浆管口至桩基外表面的水平距离.由于桩的遮蔽效应[1],在桩下游泵浆受流场扰动较小,固化土留存较多,同时结合前期数值试算结果,本文选取桩下游,泵浆管口较低的位置作为泵浆基准点,即W=1.5 m,H=14.5 m的M0点.

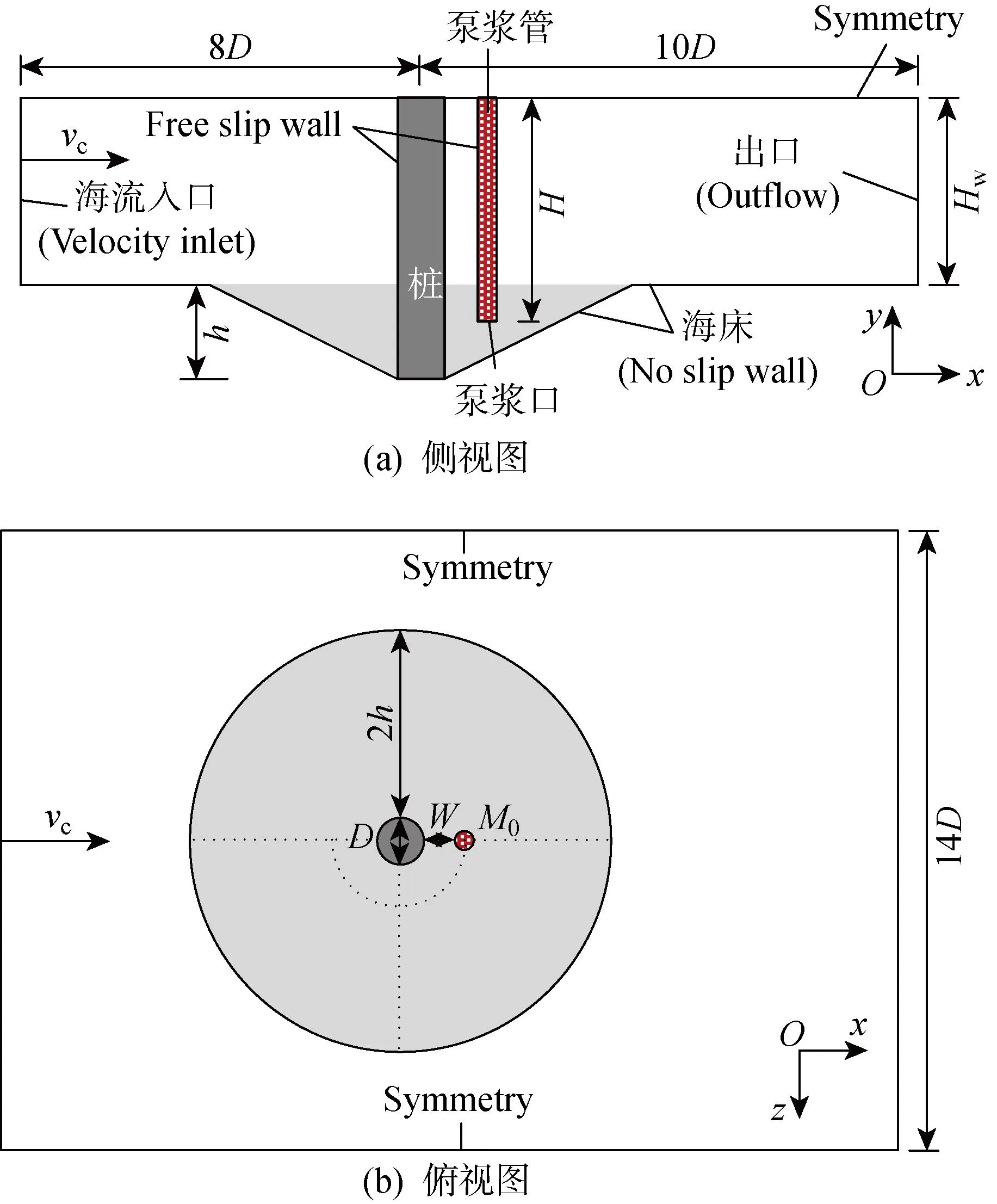
图1 几何和边界设定Fig.1 Setting of geometry and boundary condition

海流入口设置为速度入口边界(Velocity inlet),出口为自由出流边界(Outflow).计算域两侧为对称边界(Symmetry),可减小流体反射.Roulund等[17]指出当弗劳德数Fr<0.2时,可忽略空气层对水流结构的影响,因此,水流自由表面采用“刚盖假定”,即对计算域顶部也采用对称边界.底部海床面为光滑壁面(Free slip wall),其底床粗糙度(Roughness height)主要取决于沉积物粒径大小和底床起伏(比如砂脊、砂波的影响).此处不考虑底床起伏的影响,故仅采用底床沉积物中值粒径d50表征底部边界粗糙度.据李宏伟等[18]的研究可知,当底床的粒径小于1 mm时,粗糙度对流场的影响可忽略,而海床土为淤泥质粉土,其中值粒径远小于1 mm,则可以合理假设计算域的整个底部边界为光滑壁面.桩基材质为钢材,泵浆管为PVC材质,两者的表面粗糙度通常小于1 mm,同理,可忽略桩基和泵浆管表面粗糙度影响,因此数值模型中设置桩基和泵浆管表面为光滑壁面.泵浆管入口采用速度入口边界,以恒定流速泵浆.入口处水流流速为vc.

2.2 材料属性

高含水率固化土在水中流动时,可看成黏滞性非牛顿流体,采用流变模型进行描述.然而,目前关于高含水率固化土的流变特性研究十分有限.本研究参考Yin等[15]的研究成果,以初始含水率为165%,水泥掺量为200 kg/m3,盐度为0的固化伊利土的参数为本研究的基准流变参数S0.为满足泵送施工要求,固化土流动值宜为160～200 mm[19].根据Yin等[15]提出的流动值与流变参数经验关系,另补充两组材料参数S1、S2,详见表1,对材料的影响进行分析.表中:μ为黏度;τ0为屈服应力;ρ为高含水率流态固化土密度;Ds为坍落流动值.通过调研,总结得出80%～135%初始含水率的流态固化土密度ρ范围在1 350～1 600 kg/m3,本研究统一取 1 400 kg/m3.

表1 固化土浆液性质Tab.1 Properties of solidified slurry

2.3 网格划分

图2为数值模型网格划分情况.采用ANSYS Workbench的ICEM-CFD子程序对全域进行非结构化网格划分(六面体网格),最大网格尺寸为2.32 m.由于桩基和泵浆管附近流场变化复杂,也是需要重点关注的流场区域,因此对桩周和管周进行局部网格加密细化,网格尺寸为0.5 m.总网格数达到53.4万.

图2 网格特性Fig.2 Characteristics of grid

2.4 求解设定

本数值计算采用瞬态分析方法.不同工况泵送固化土的总量保持恒定,即212 m3.计算结束时间取决于泵送固化土的速度.以泵速vm=2.5 m/s为例,计算总时长为45 min=2 700 s,计算时间步长取0.02 s.多相流计算时,压力场和速度场的耦合采用Phase Coupled SIMPLE算法求解,空间离散采用二阶迎风格式,基于单元的最小二乘法用于梯度的数值逼近,瞬态项选用二阶迎风差分格式.

2.5 方法验证

在进行数值研究之前,需要对流态固化土与单桩相互作用的数值模型进行验证.目前,在海洋环境中泵送固化土的研究十分有限,没有直接相关的试验或者数值数据可参考.考虑到固化土在泵送过程中时变性可忽略,泵浆阶段的高含水率固化土在水下的运动可视为泥浆在水中流动,流动过程中对桩基础的作用可视作水下流动的泥浆对桩基础的作用.因此,本文将数值模拟结果与文献[10]中的室内试验结果进行对比,以验证流态固化土与单桩相互作用的数值模型的可靠性.该试验以泥浆在水下的流动模拟海底滑坡运动过程,分析海底滑坡与缓坡海床上的单桩的相互作用.本文参考该物理模型试验,建立两相流数值模型,具体的数值模型建立过程可参见Li等[11]的研究.将数值计算结果与文献[10]中的试验结果进行了对比,如图3所示.图中:CD为阻力系数;Renon为非牛顿流体的雷诺数.从结果对比图3可以看出,不同泥浆性质和泥流流速条件下(即泥流的雷诺数不同),水下流动的泥浆与桩基的相互作用力的数值结果与试验结果在整体趋势上保持一致.因此,可认为该数值模型能较好模拟水下泥流对单桩的作用过程,输出结果有效且可靠,即该数值模型可应用于初始阶段流态固化土在水下流动过程中对单桩的作用力分析.

图3 数值方法和模型验证Fig.3 Verification of numerical method and model

3 结果讨论

3.1 影响因素分析

对沿水深整个桩基上所受的合力Fx进行分析.合力Fx以顺水流方向为正值,由水流和流态固化土两部分贡献.

为研究动水条件下流态固化土对桩基所受合力的影响,设计单因素数值试验,考虑vc,vm和固化土类型的影响.以东海大桥风电场为例[20],水流流速通常为0.5～2.5 m/s,根据现场实际推算出泵送速度的范围为2～3 m/s,固化土类型考虑S0、S1、S2这3种不同流变参数的固化土,设计工况如表2所示.以vc=1 m/s,vm=2.5 m/s,固化土S0为基准工况.工况2～4旨在探究水流流速影响,工况6～10研究泵送速度的影响,工况11和12关注固化土类型的影响.

表2 单因素分析计算工况Tab.2 Single factor analysis

图4所示为vc,vm和固化土类型(不同流动值及流变参数)这3种因素对桩上合力的影响.由图4(a)可见,随泵浆过程发展,合力最终都归于稳定峰值.当流速较小(vc≤0.5 m/s)时,合力稳定峰值为负值,这归因于流态固化土在逆水流方向的作用贡献.当流速较大(vc>0.5 m/s)时,合力稳定峰值为正值,且随流速增大,水流力贡献越来越大,稳定峰值不断增大.相较于基准工况(vc=1 m/s),vc增至2.5 m/s,可使合力稳定峰值增大 1 209.57%.由图4(b)可以看出,泵送速度的变化对桩上受合力影响不大,虽然泵送速度不低,但泵送方向保持为竖直向下的情况下,流态固化土并不会对桩结构产生直接的冲击,而且水环境也会对固化土浆液的流动产生阻力.图4(c)中,当流态固化土流动值较大(流变参数较小,S0)时,合力峰值为正值,此时为水流作用主导.当流态固化土流动值较小(流变参数较大,S1/S2)时,合力峰值为负值,且随流动值减小(流变参数增大),流态固化土在逆水流方向的作用贡献越来越大,合力峰值不断减小.相较于基准工况S0,S2流态固化土为合力峰值带来的变化达到490.91%.

图4 参数分析Fig.4 Parameter analysis

为进一步探究多因素的综合影响,理清各因素影响的相对大小,设计正交数值试验,进行参数敏感性分析,参数设定如表3所示.采用L9(33)正交表,科学全面地选择9个工况.相较于全面试验的27个工况,正交试验设计极大减少工作量.正交数值试验设计如表4所示.正交试验结果分析曲线如图5所示.图中:Fxp, a为某影响因素在某一水平条件下所有工况的合力峰值的平均值.

表3 因素和水平Tab.3 Factors and levels

表4 正交试验Tab.4 Orthogonal tests

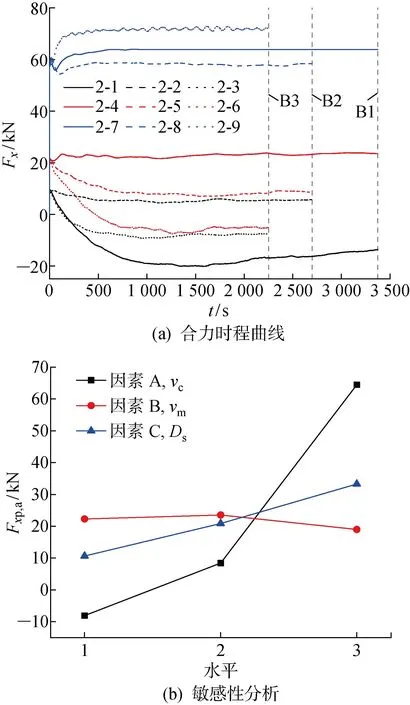
图5 正交试验结果分析Fig.5 Results of orthogonal tests

图5(a)为正交试验结果的时程曲线,可以看出,泵浆初始时刻,桩上合力大小仅取决于水流流速,开始泵浆以后,或上升或下降至稳定峰值,桩身受力受水流速流、泵送速度和固化土性质的综合影响.本文采用极差分析方法[21]对合力峰值(Fxp)进行参数敏感性分析.极差分析法也称R法,是一种针对正交试验数据的分析方法.该方法可通过计算R值(因素极差值)来判断影响因素的敏感情况.该方法先计算某个影响因素在某一水平条件下所有工况的试验数据的平均值Kavg,然后对该因素在不同水平条件的Kavg的波动情况进行分析,Kavg的极差值即为R值.某影响因素的R值越大,意味着该影响因素对结果影响越显著,即该因素越敏感.本文评价各影响因素对合力峰值的影响显著性,先计算出各影响因素的Fxp,a,结果如图5(b)所示.从Fxp,a的波动范围来看,随水平变化,水流流速的波动范围最大,即水流流速的R值最大.因此,水流流速对合力峰值的影响最大,其次是固化土类型,泵送速度影响最小.

3.2 流态固化土对桩基作用力与波、流作用力的对比

如上分析,桩上合力Fx由水流和流态固化土共同作用产生.采用合力指标忽略了两部分各自产生的力在作用点和方向上的差异,不能全面评价两部分力对桩的效应,因此,需要单独对两部分产生的作用力进行探究.首先,以单因素分析的基准工况为例,即vc=2.5 m/s,vm=1 m/s,固化土S0,对静水中流态固化土对桩的作用力Fx0和纯水流对桩的作用力Fxc的量级进行评估,值得注意的是,Fx0和Fxc方向相反.各作用力随时间变化如图6所示.

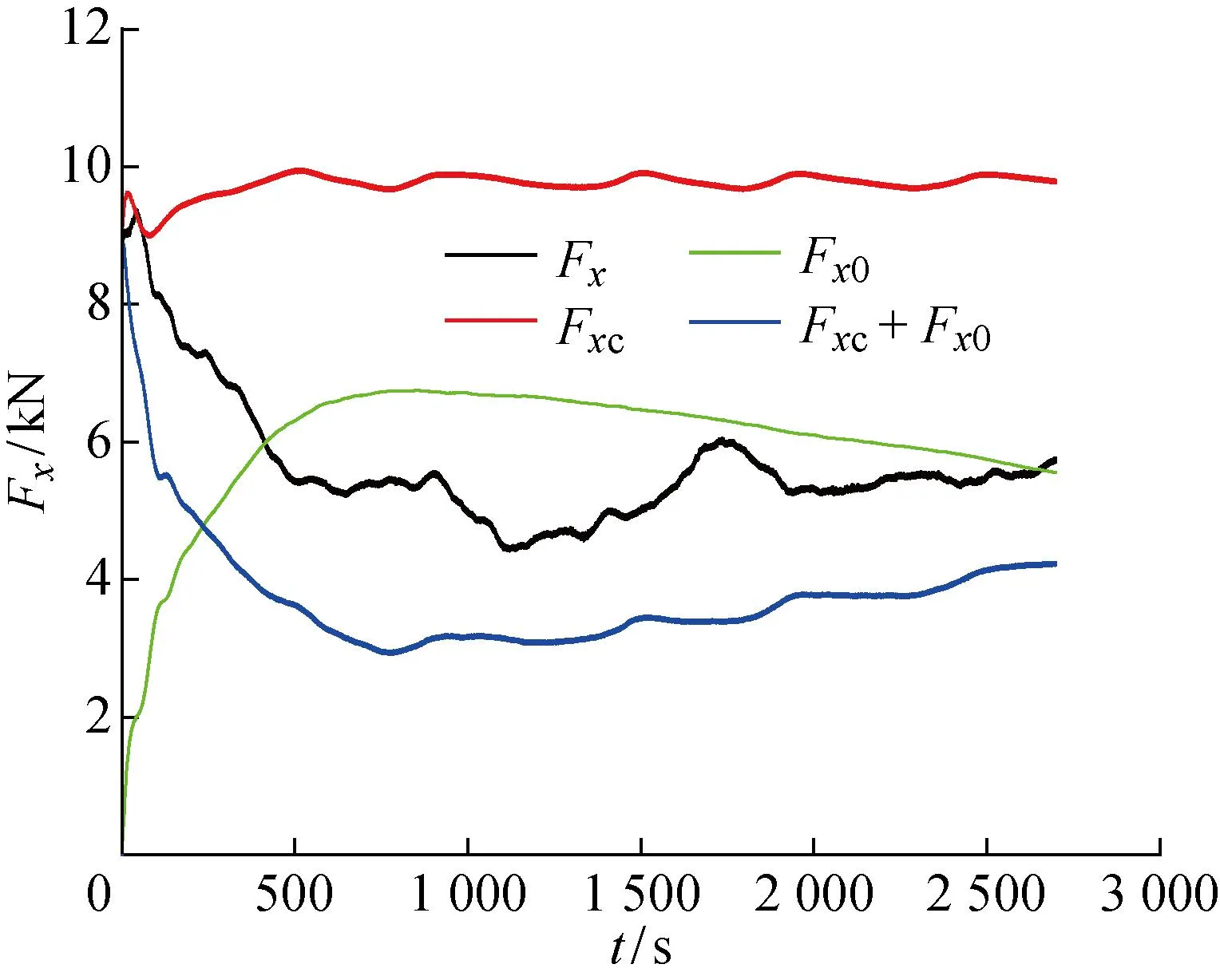
图6 桩上作用力随时间变化Fig.6 Force acting on monopile

由图6可见,水流与流态固化土共同作用的合力Fx略大于纯水流作用与静水中流态固化土作用的叠加值Fxc+Fx0,差距较小,两者量级一致.因此,在计算桩上所受作用力时,可采用解耦分析思路,单独考虑静水中流态固化土对桩的作用力,再与海流等海洋环境荷载叠加.

事实上,海洋桩基同时受波浪、海流等作用,在对采取固化土冲刷防护措施的桩基承载力进行核算时,需考虑波流共同作用.为进一步评估该解耦分析思路的可行性,采用数值方法计算得到静水中流态固化土对桩的作用力峰值,并同时采用数值方法或《海港水文规范》[22]、《港口工程荷载规范》[23]计算桩上的波流共同作用力,对计算出的各作用力大小进行对比分析.选用东海风电场附近海域50年重现期的波浪参数:平均波高2.83 m,波周期7.76 s,波长74.1 m.潮流流速选用设计平均流速2.39 m/s[20].流态固化土类型为S2,泵速取3 m/s.计算结果如图7所示.

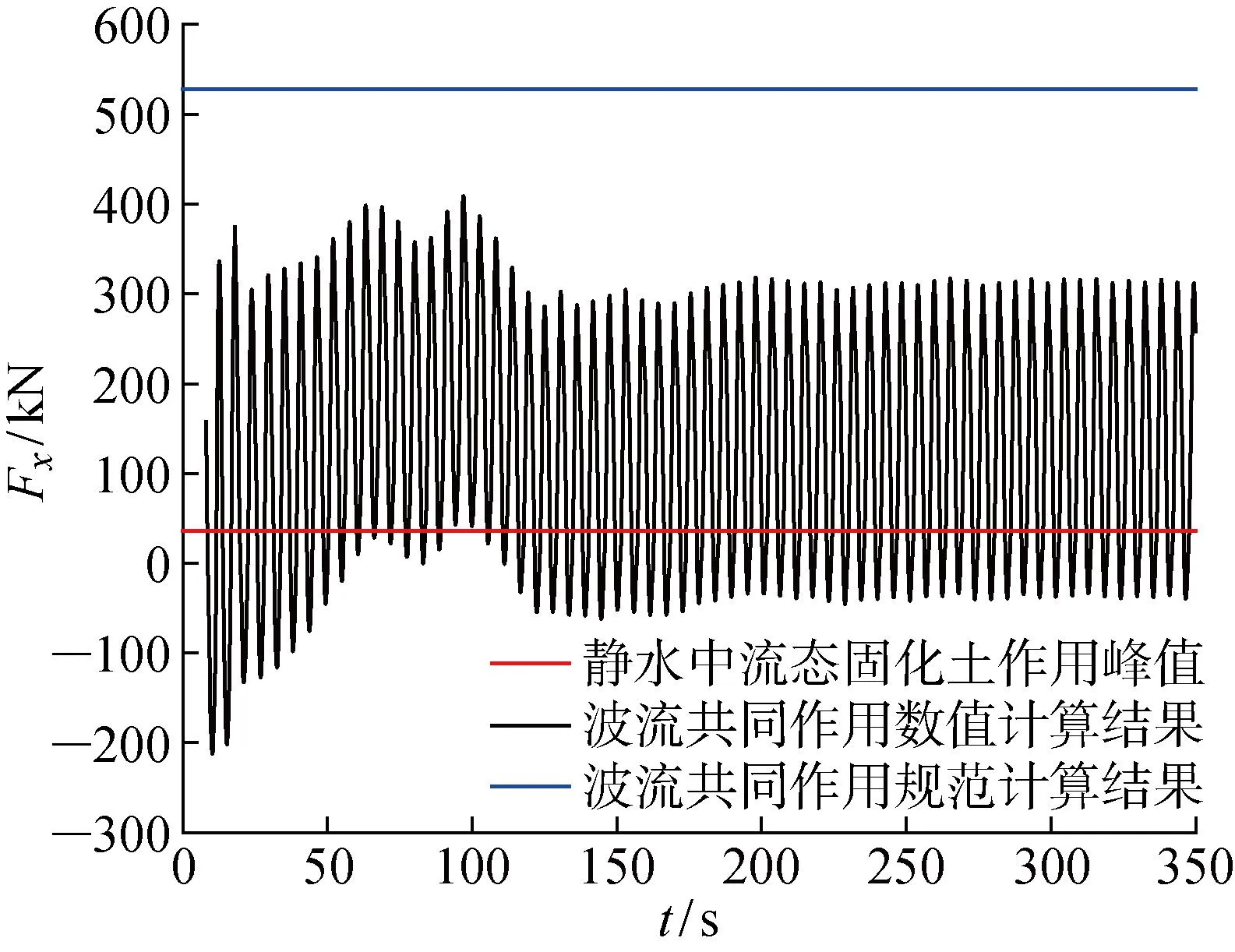
图7 桩上不同力对比Fig.7 Comparison of force acting on monopile

可以看出:数值计算得出的波流共同作用力平台段峰值316 kN与静水中流态固化土对桩基的作用力峰值35.6 kN的叠加值为351.6 kN,小于波流共同作用力的规范计算结果528 kN,说明采用解耦分析思路计算出的桩上作用力是安全保守的.因此,本文建议,在实际工程中,对需要采取固化土冲刷防护措施的桩基承载力进行核算时,桩上作用力可采用上述解耦分析思路求解,先对静水中流态固化土对桩的作用力进行计算,再与波流等海洋环境荷载叠加.

3.3 流态固化土对桩基作用力经验公式

目前,关于海洋桩基所受波流等荷载计算已经有较多研究成果和规范可供参考.然而,尚未有关于流态固化土对桩基作用力的研究.针对流态固化土会对桩基产生不利影响的问题,采用计算流体动力学方法,模拟了静水中单桩基础周围冲刷坑中流态固化土泵送过程,评估流态固化土对桩基础的作用力.下面对固化土类型和泵速影响进行定量分析.模拟S0、S1、S2共3种类型固化土,2、2.5、3 m/s这3水平泵速,共9种工况.

本研究中,流态固化土作用力方向为逆水流方向,皆为负值,本研究只关注其大小,即取绝对值.图8为静水中流态固化土对桩基作用力大小的时程曲线.可以看出,固化土流变参数越小(流动值大)时,作用力大小逐步上升至平台段;固化土流变参数越大(流动值小), 作用力大小初期上升后略微下降,下降趋势愈发明显.这主要是因为固化土流变参数越大(流动值越小),流动性越弱,容易在桩一侧堆积,进而产生桩前后压差,导致峰值出现[24],如图9所示.图中:Hp为1-1截面与数值计算域顶部的距离,本文取14 m;采用流态固化土体积分数φm表征流态固化土流动形态;pm为流态固化土桩周压力.

图8 静水条件泵送固化土对桩基作用力大小随时间变化Fig.8 Distribution of force acting on monopile in static water with time

图9 单桩周围的固化土流动形态及压力分布图Fig.9 Shape of solidified slurry and pressure distribution around monopile

流态固化土对桩基作用力峰值Fx0, p为最不利情况,对其进行量化分析评估.固化土类型与泵速对作用力峰值影响如图10所示.可以看出,随泵速和固化土流变参数增大(流动值减小),作用力峰值呈线性递增趋势.因此,对Fx0,p、Ds和vm进行无量纲化处理,并采用多元线性回归方法对结果进行拟合,提出无量纲峰值作用力F′的经验公式:

图10 静水条件下泵送固化土对桩基作用力峰值变化Fig.10 Peak value of force acting on monopile in static water

(6)

式中:重力加速度g=9.806 m/s2;管径d=0.2 m;流动值试验采用的标准有机玻璃圆筒直径Ds0=0.08 m,拟合优度为0.95.其中,无量纲的峰值作用力F′ 表达式如下:

(7)

式中:海水密度ρw=1 000 kg/m3;Hw+h为冲刷坑底的水深16 m;D=5 m.实际工程中,可利用经验公式对静水中流态固化土对桩基作用力进行快速评估,结果可作为现场施工的控制依据.

4 结论

本研究采用计算流体动力学方法,结合东海大桥海上风电场实测水文资料,模拟了桩基础周围冲刷坑中流态固化土泵送过程,分析了泵送过程中海洋桩基受力变化,得到如下结论:

(1) 泵送流态固化土过程中,桩身所受作用力由海流流速、固化土性质以及泵速共同决定.海流流速越大,流态固化土流动值减小(流变参数增大),泵速增大,对桩所受作用力的贡献越大.其中,海流流速因素对桩身受力影响最大,其次是固化土类型,泵浆速度影响最小.

(2) 通过与波、流作用做对比,单独考虑静水中流态固化土对桩的作用力,再与波流共同作用力叠加的解耦分析思路具备可行性,提供了一种在桩基防冲刷施工作业中考虑流态固化土作用的简化计算方法.

(3) 基于因冲刷导致的桩基础承载力弱化现状,提出了静水中流态固化土对桩基作用力峰值综合经验公式,结合风浪流力相关规范,实现快速评估泵浆过程中桩受的作用力,结果可作为现场施工的控制措施的依据.

致谢本文作者对国家自然基金、上海市科学技术委员会以及对本研究提供指导和建议的相关人员表达衷心的感谢.