隧道周围饱和软土二维非线性固结分析

胡安峰, 龚昭祺, 肖志荣, 陈 缘

(1. 浙江大学 滨海和城市岩土工程研究中心, 杭州 310058; 2. 浙江省建筑设计研究院, 杭州 310006;3. 浙江大学建筑设计研究院有限公司, 杭州 310028; 4. 浙江大学平衡建筑研究中心, 杭州 310028;5. 浙江科技学院 土木与建筑工程学院, 杭州 310023)

隧道周围土体固结主要与土体性质、盾构施工、衬砌渗漏和交通荷载等因素相关.其中,盾构施工过程会对隧道周围土体造成扰动,在地下水丰富的地区由于盾构推进的挤压和压浆等作用表现为产生超静孔隙水压力.因地面透水以及隧道损伤导致透水通道的形成,超静孔压会逐渐消散,从而引起隧道周围土层发生固结与沉降.同时,软土在固结过程中压缩性与渗透性具有非线性变化的特性,使得隧道周围土体固结问题更为复杂.

目前,关于盾构隧道渗漏和固结问题的研究方法主要有现场实测法、数值模拟法和解析法.蒋洪胜等[1]、陈宇等[2]通过实测隧道初始超静孔压,给出了超静孔压的分布范围及不同位置处的大小;魏新江等[3]提出盾构施工后土体超静孔压分布范围及计算公式,但仍需实测数据验证;Shi等[4]利用粉质黏土芯样一维固结试验获得的固结变形比估算固结沉降,并依此研究煤矿倾斜盾构通道的稳定性;Mair等[5]通过将地表沉降剖面与地层沉降进行对比,发现可用高斯曲线描述由隧道开挖引起的地表沉降;Jallow等[6]利用Plaxis 3D模型分析了盾构施工诱发的长期沉降机理,通过与实测数据对比,评估了固结对长期沉降的影响.Shin等[7]研究了盾构管片和周围土体之间的力学和水力耦合作用,考虑盾构隧道因各种因素导致的水力条件恶化,提出了一种渗漏控制和评估方法;Wu等[8]采用一维渗漏单元模拟衬砌局部渗漏以减小计算误差,研究结果表明,地下水渗漏导致隧道周围孔隙水压力降低,衬砌顶部渗漏对地表沉降有较大影响; Huangfu等[9]基于复变量方法推导得到二维稳态地下水渗流解析解,计算得到隧道周围土体中孔压场分布;郑永来等[10]通过有限元分析了隧道衬砌不均匀渗漏条件对地表长期沉降的影响;詹美礼等[11]统一考虑土体流变及渗流,采用坐标映射的方法,获得了隧道周围土体孔压消散及固结解析解,但并未考虑土体在固结过程中压缩性与渗透性的非线性变化;Zhang等[12]采用Boltzmann模型描述土体的黏弹性,并将列车荷载简化为三角形循环荷载,对盾构隧道周围土体长期沉降进行了解析求解.

综上所述,诸多学者利用各种方法研究了隧道施工、透水条件、土体流变和列车荷载等因素对固结沉降的影响规律,但是在现有的研究中,考虑隧道周围软土压缩性和渗透性变化的尚不多见.然而在土体固结过程中,随着孔隙水压力的消散和有效应力的增加,土体压缩性和渗透性将随着孔隙比的减小呈现出非线性变化,进而对土体固结规律以及沉降发展产生重要影响.尽管曹奕[13]在隧道周围土体固结分析中,考虑了土体压缩性和渗透性的非线性变化,但遗憾的是,他采用的分析方法无法获得整个场域上的解答[14].因此,本文基于渗透系数和有效应力随孔隙比变化的非线性模型,建立二维固结控制偏微分方程,并利用一种交替隐式差分法对方程进行了求解,获得了在不同透水条件下隧道周围全场域软土的非线性固结解答,研究了软土非线性参数Cc、Ck和Cc/Ck对固结性状的影响规律.

1 问题描述

计算简图如图1所示.图中:H为土体厚度;h为隧道中心埋深;B为隧道一侧土体宽度;r1和r2分别为隧道内外半径.地基表面排水,左右两侧及底部不排水,隧道衬砌考虑完全透水、完全不透水以及半透水3种情况.

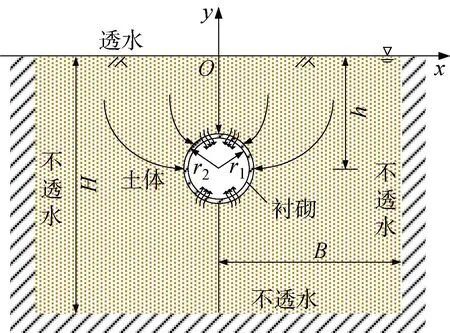
图1 计算简图Fig.1 Computing model

基本假定为:① 隧道在纵向无限长,满足平面应变条件; ② 土体饱和,土颗粒和孔隙水不可压缩,孔隙水流动服从 Darcy定律; ③ 变形为小变形; ④ 地基中各点土体所承受的竖向总应力不随时间变化; ⑤ 地基内各点土体自由变形,不受土体自身或隧道成拱作用带来的影响.

2 控制方程

由土单元体内水量的变化率等于土体积变化率,可得基本控制方程为

(1)

式中:γw为水的重度;ks为土体渗透系数;u为超静孔压;εv为土体体积应变;t为固结时间.

土体的压缩性和渗透性服从如下规律[15-16]:

(2)

(3)

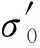
由式(2)和(3)可得:

(4)

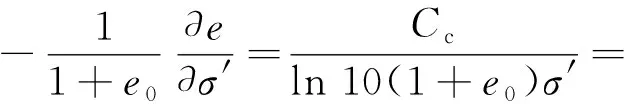
(5)

式中:mv为体积压缩系数;mv0为初始体积压缩系数.

由有效应力原理:

(6)

以及:

(7)

联立式(5)得:

我国国家卫生计生委也提倡建设节约型医院，各医院纷纷响应国家号召，在制定节能计划之前，引进一套有效的能耗监测系统，对医院各科室的水电气能耗进行能耗监测，以掌握全院能耗动向，分析用能分布，制定节能考核指标，以达到节能降耗的目的。有了能耗监控系统，医院管理者对本院的能耗指标的监控和管理更加容易。将系统得到的能耗分项和分析报表进行科学的分析，进而制定相关节能举措。

(8)

将式(4)和(8)代入式(1)可得二维非线性渗流固结控制方程:

(9)

边界条件如下:

(1) 地表处为完全透水,即y=0时,u=0.

其中:κ为衬砌与土体的相对渗透性系数;kl为隧道衬砌渗透系数.当κ=0时,隧道完全不透水;当κ趋向无穷时,隧道完全透水;而处于半透水状态时,需考虑衬砌与土的渗透系数、衬砌尺寸效应,孔压梯度与孔压正比例相关[15].

初始条件如下:

u|t=0=u0

(10)

式中:u0为初始超静孔压,根据现有文献研究结果,软土盾构壁后初值u0=30 kPa,并按照相同的模式沿隧道径向衰减[1,11].

3 有限差分法求解

由于式(9)为非线性方程,目前该固结控制方程只能在一系列严格假定的情况下获得解析解[13],而且解析方法存在部分场域不可解的问题,所以难以获取全场域解答.有限差分法是一种可将时空离散化的近似方法,可以求解任意偏微分方程形式下时间和空间位置处的解,因此,本文采用有限差分法进行相应求解[16-18].为避免差分方法中显示差分因时间步长和空间步长造成的稳定性差问题[19],文中采用一种交替方向隐式差分法(ADI).每一时间步的网格剖分如图2所示,由于网格剖分坐标系为笛卡尔坐标系,所以隧道边界的圆形近似处理为多边形.

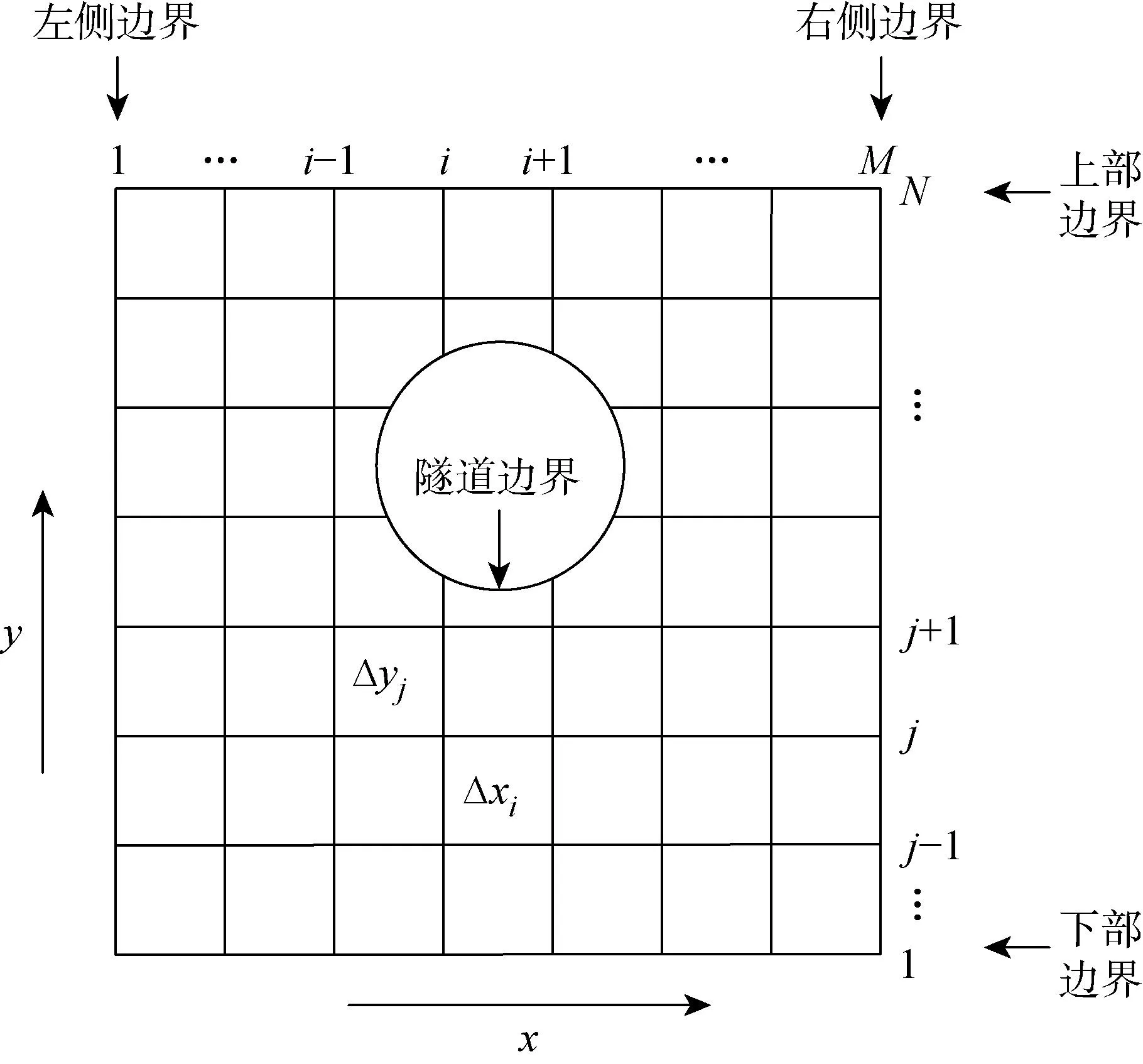
图2 网格剖分示意图Fig.2 Schematic diagram of mesh division

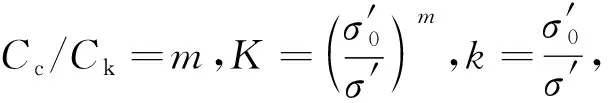
(11)

(12)

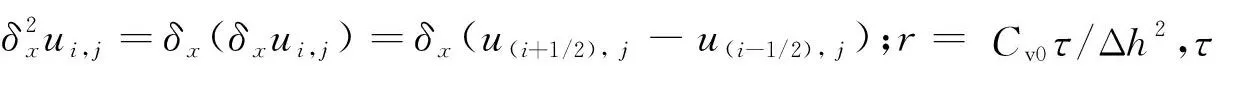
引入初始超静孔压u0,分别按式(11)和(12)计算得到下一时间步的超静孔压场分布,按固结度定义即可计算得到固结度;再将当前得到的超静孔压作为下一时间段内的起始孔压,循环计算直至得到终止时刻的孔压和固结度,计算流程图如图3所示.

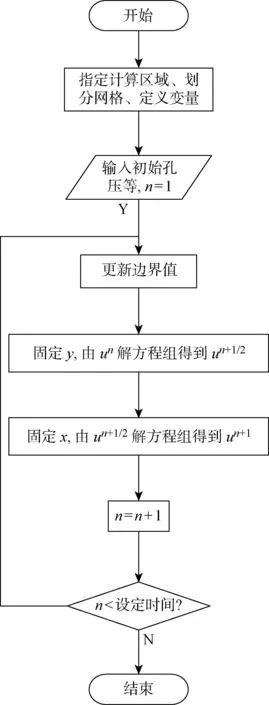
图3 差分计算流程图Fig.3 Flow chart of finite difference calculation

4 验证与分析

根据有限差分格式和相关计算流程,编制了MATLAB计算程序.为验证计算方法的正确性,将本文差分解与已有的Terzaghi-Rendulic固结方程解析解[13]进行计算对比.在此基础上,考虑了隧道不同透水条件,研究了Cc、Ck等参数对固结性状的影响.研究表明,Cc/Ck取值范围一般为0.5～2.0,大多为0.5～1.0[20],结合杭州萧山软土GDS固结试验[21],本文分别取Cc/Ck=0.50,0.75,1.00,1.25进行计算分析.隧道几何参数与物理参数为[13]:h=11 m;r1=2.75 m;r2=3.10 m;ks0=5.40 nm/s;e0=1.40;Cc=0.25;土的重度γs=18 kN/m3.

4.1 验证

平均固结度U采用超静孔压来计算,如下式所示:

(13)

式中:si,j=ΔxiΔyj为离散点(xi,yj)处空间步长所围面积.

当不考虑土体在固结过程中压缩性与渗透性的非线性变化时,式(9)所表示的固结方程即退化为Terzaghi-Rendulic固结方程.为验证计算方法的正确性,将退化解与Terzaghi-Rendulic固结方程解析解进行了对比分析,具体结果如表1所示.

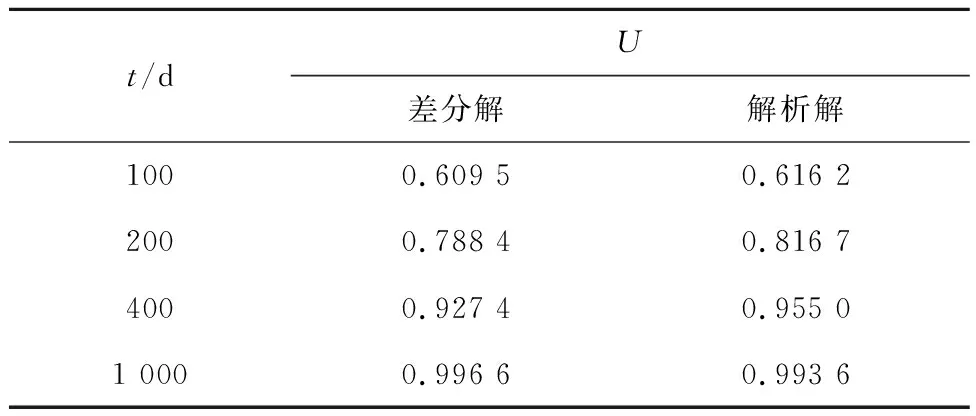
表1 差分计算结果与解析解对比Tab.1 Comparison of results obtained by finite difference method and analytical method

由表1知,差分解与Terzaghi-Rendulic固结解析解基本一致,最大误差不超过3.6%,说明了计算方法的正确性,两者存在较小差别的原因可能是两种计算方法的边界不完全重合.

图4给出了衬砌完全透水情况下超静孔压随时间消散的云图.由图可见,所采用的计算方法能正确反映超静孔压的消散规律.

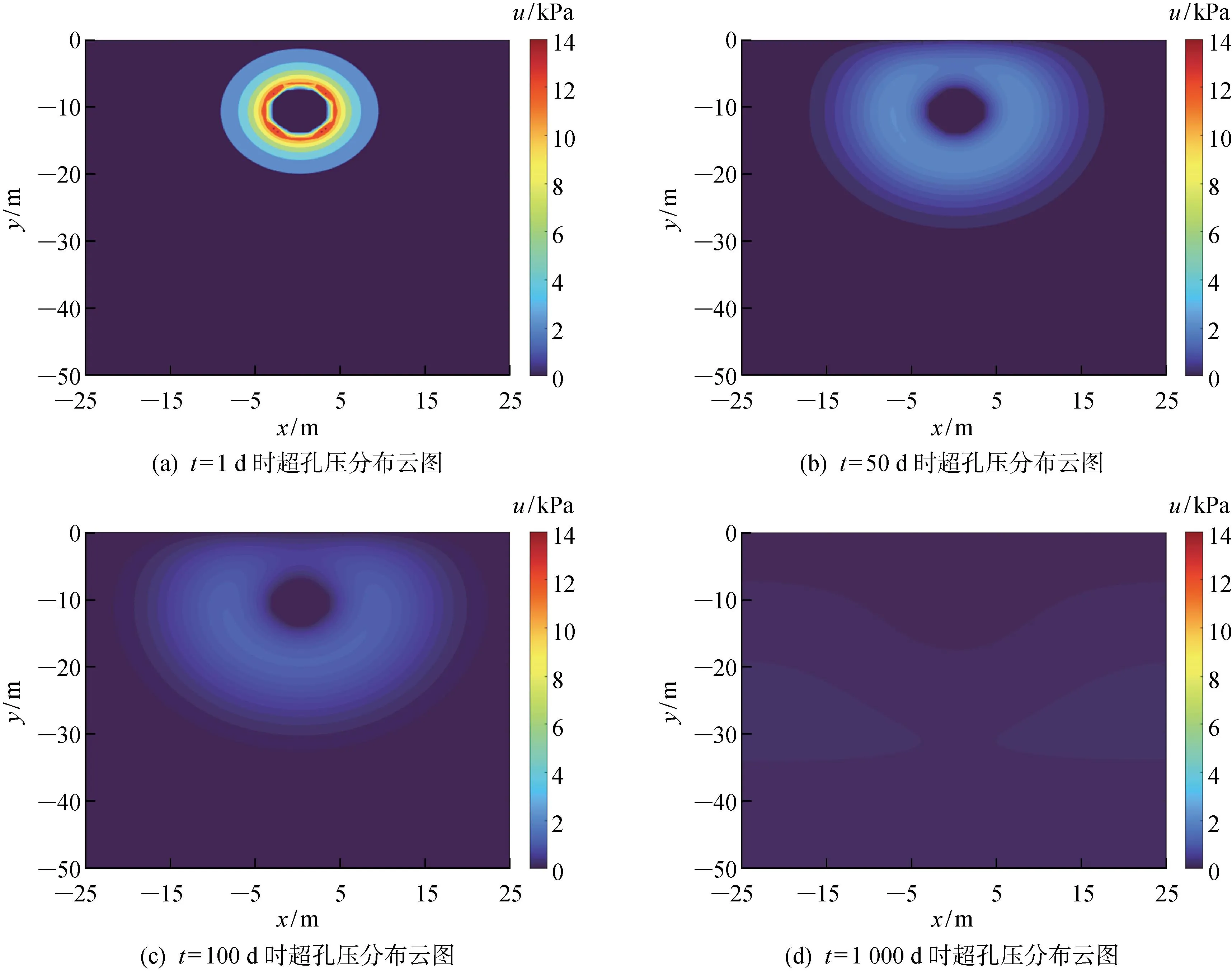
图4 不同时间超静孔压分布云图Fig.4 Nephogram of excess pore water pressure distribution at different times

4.2 隧道透水条件对固结特性的影响

为研究隧道不同透水条件对固结的影响,分别取隧道完全透水、半透水(取kl/ks0=0.001,0.01,0.1)、完全不透水时计算土体的固结度(见图5).

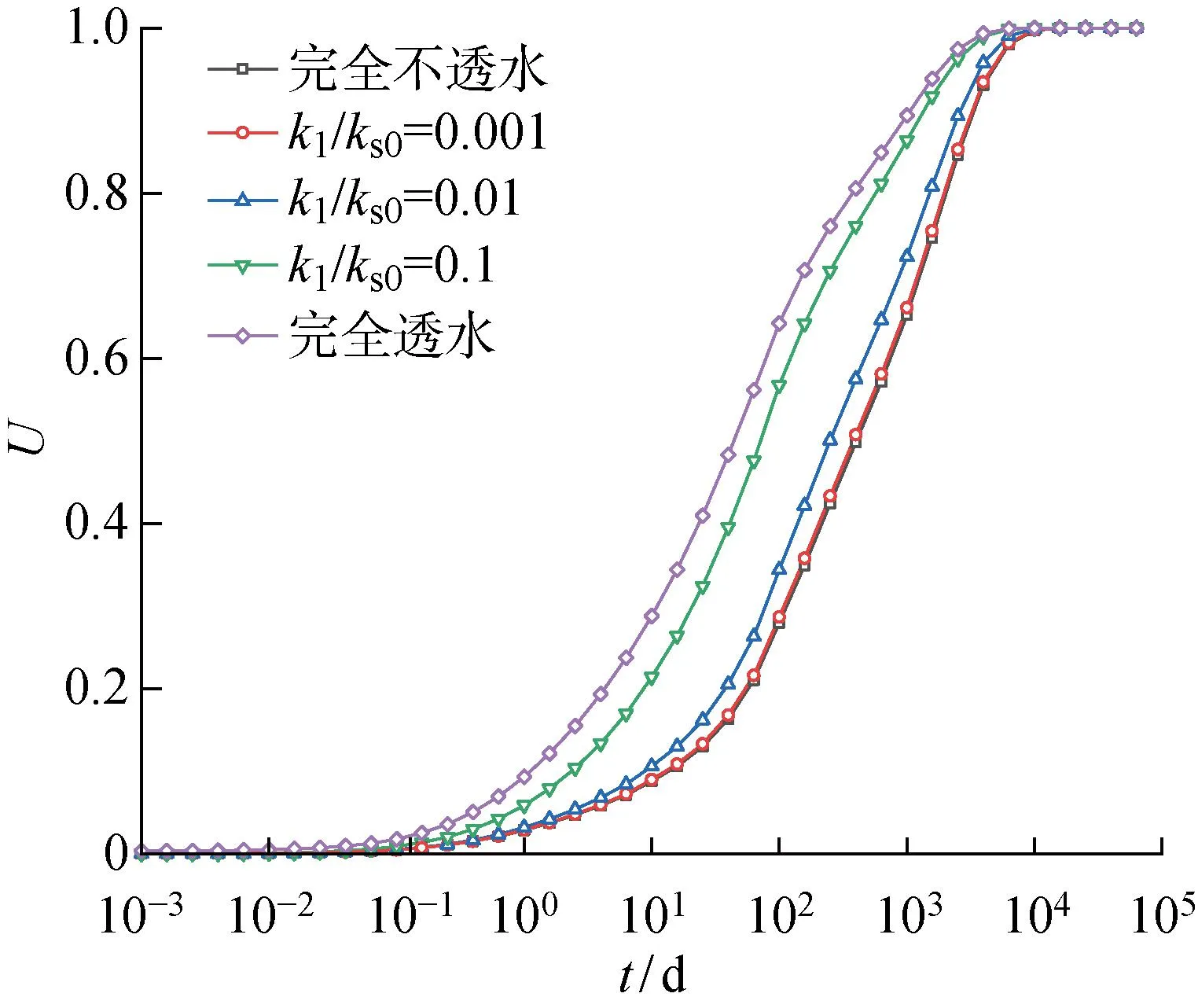
图5 不同隧道透水条件下固结度Fig.5 Degree of consolidation under different tunnel permeability conditions

由图5可见,前1 000 d不同隧道透水条件下的固结速率均较大,固结度发展随时间推移均趋于平缓.这是因为随着土体的固结,超静孔压逐渐消散,土体有效应力不断增加,孔隙比不断减小,导致体积压缩系数和渗透系数不断减小,土体固结不断减慢.随着隧道透水能力的增强,在相同固结时间内固结度越来越大,完全透水情况下,因隧道透水能力强,孔压消散速率快,与完全不透水情况相比固结度最大相差达36.3%,达到完全固结所需时间减少.

4.3 Ck对固结特性的影响

图6为Ck对隧道周围土体平均固结度发展的影响情况.由图可见,当Cc值相同时,不同Ck值对固结影响显著,Ck值越小,相同时间内固结度越大,平均固结度最大差值超过20%.图7给出了某一时刻土体中初始有效应力与当前有效应力之比的云图.结合图6和图7可见,在渗流固结过程中,土体中有效应力将产生重分布现象,在固结发展过程中,部分区域土体的有效应力减小,此区域内固结速率随着Ck的减小而增大,但对于有效应力增大的区域,固结速率却随着Ck的增大而增大.由于Ck在有效应力减小区域对整体固结度发展的影响更为显著,所以最终的整体平均固结度呈现出随Ck值减小而增大的效果.

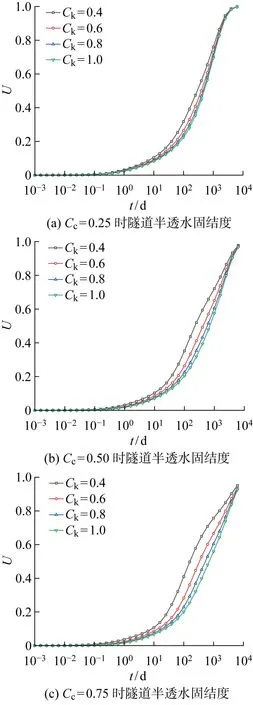
图6 Ck对隧道周围土体固结度的影响Fig.6 Influence of Ck on consolidation degree of soil around tunnel

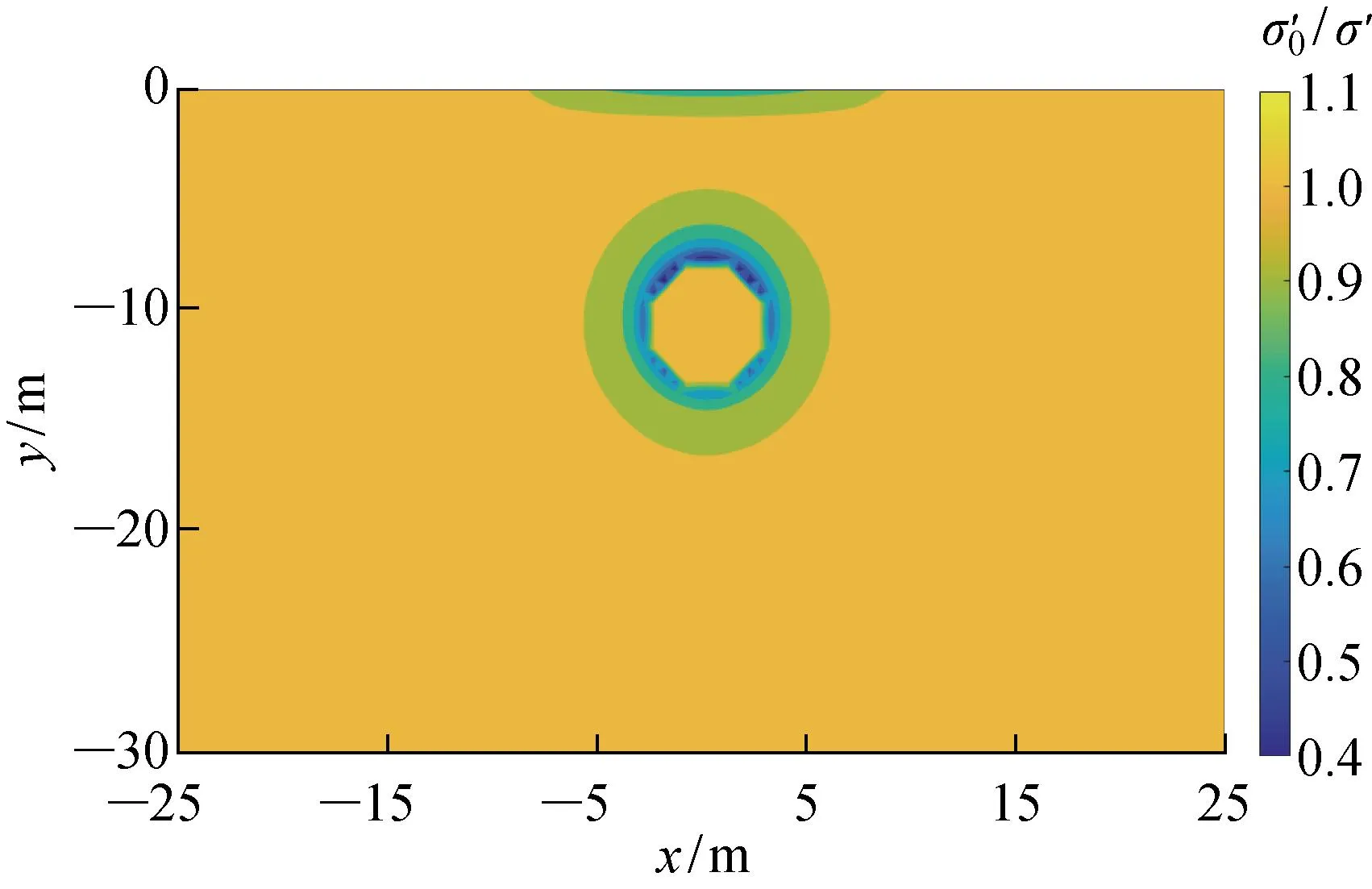
图7 某时刻云图 cloud map at a certain time

4.4 Cc对固结特性的影响

图8为Cc对隧道周围土体平均固结度发展的影响情况.由图可见,当Ck值相同时,Cc对固结度发展的影响总体不大,尤其在固结发展前期,曲线间距较小.在固结发展后期,Cc值越大相同固结时间内固结度越小.同时,对比图6可以看出,在相同条件下,渗透指数Ck比压缩指数Cc对固结度的发展影响更为显著.Cc对固结特性的影响原因与4.3节分析类似,此处不一一赘述.

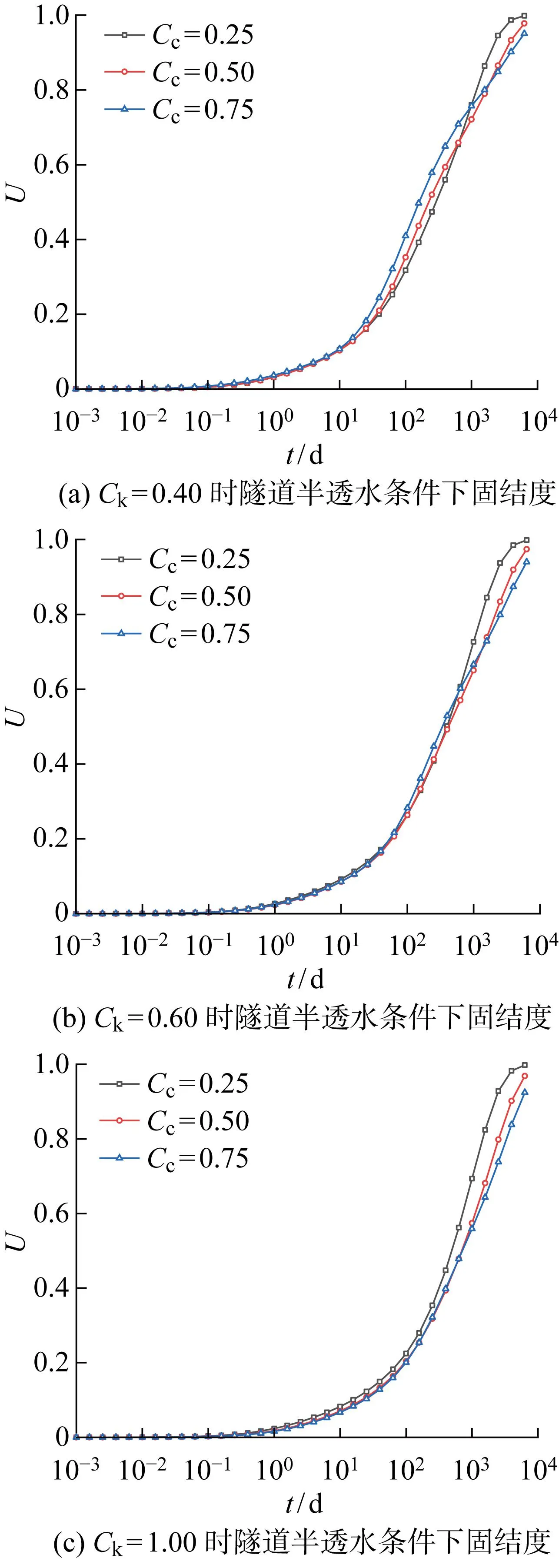
图8 Cc对隧道周围土体固结度的影响Fig.8 Influence of Cc on consolidation degree of soil around tunnel

4.5 Cc/Ck对固结特性的影响

目前,隧道周围软土非线性固结解析中仅考虑渗透系数与压缩系数同步变化,即Cc/Ck=1.图9所示为Cc/Ck对隧道周围土体固结度的影响.由图可见,隧道周围土体固结度随Cc/Ck值的增大而增大.当Cc/Ck<1,=1,>1时,相同时间内固结度发展差异较大,最大差值近15%.因此,在计算分析中必须考虑渗透系数与压缩系数的非同步变化,才能得到更为精确的计算结果.同时,从图中还可以看出,非线性解与线性解的差别也较大,因此在计算分析中考虑非线性尤为必要.平均固结度随Cc/Ck的增大而增大,原因分析同4.3节.

图9 Cc/Ck对隧道周围土体固结度的影响Fig.9 Influence of Cc/Ck on consolidation degree of soil around tunnel

5 结论

通过引入e-lgk与e-lgσ′模型,建立了隧道周围土体二维非线性固结控制方程.针对现有理论解析的不足,运用有限差分法对控制方程进行求解,考虑了隧道不同透水条件、Cc和Ck不同取值的影响,研究了隧道周围土体固结发展规律,主要结论如下:

(1) 本文采用的差分法解决了解析法中解析域不完整的问题,可以求得整个计算域上的孔压分布以及消散规律.

(2) 隧道透水情况对固结度的发展影响显著,相同时间内3种透水情况对应的固结度差异较大;当隧道为半透水条件时,随着衬砌渗透系数与土体初始渗透系数比值kl/ks0的增大,相同固结时间内固结度越大.

(3)Cc和Ck均是影响固结发展的重要因素.渗透指数Ck对固结度的发展影响相较于Cc更为显著.在有效应力减小区域Ck值对整体固结度发展的影响显著.

(4) 在隧道周围土体固结分析中,考虑非线性以及渗透系数与压缩系数的非同步变化尤为必要.