耦合Kundu-Eckhaus方程的局域波解及其动力学特性
刘 然,郭明敏,宋 妮
(中北大学 数学学院,山西 太原 030051)
0 引 言
近年来,非线性方程的局域波研究受到众多学者的广泛关注。局域波按照其传播方式[1],主要包括孤子、呼吸子和怪波。孤子在不受外界阻力影响状态下,具有稳定结构的波包和很好的粒子性[2-3]; 呼吸子是一类具有呼吸特点的特殊非线性波,以局域振荡的方式存在,与背景场之间存在周期性能量交换[4]; 怪波是一类短寿命且具有高能量的局域波,极具瞬时性和偶然性,其振幅高度至少超过背景场2倍以上[5-6]。一般情况下,数学物理问题可通过非线性微分方程来描述,这对揭示局域波的动力学特性具有重要的作用[7]。
非线性薛定谔(NLS)方程常用于研究局域波,Kundu-Eckhaus(KE)方程[8]是NLS方程的可积推广,也是分析局域波动力学特性的一个重要模型[9]。到目前为止,已经有不少学者对KE方程进行了研究。Zhai等[10]运用广义Darboux变换得到三分量耦合NLS方程的怪波解,Qiu等[11]利用Darboux变换构造出二分量KE方程的怪波解,Qi等[12]阐述了五次非线性项对超短光脉冲在non-Kerr光纤中传播的影响,扎其劳[13]利用广义Darboux变换对KE方程的一阶怪波和二阶怪波进行了研究,邱德勤等[14]进一步发展了KE方程,给出耦合KE方程的N阶Darboux变换,得到该方程的高阶怪波解,Deng等[15]基于Hirota双线性法得到了KE方程的N阶孤子解。
基于上述工作,本文将研究耦合三分量KE方程
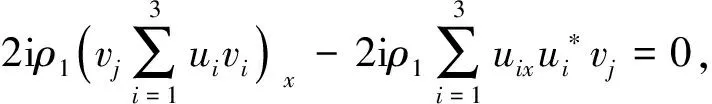
(1)
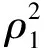
1 广义Darboux变换
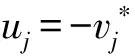

Φt=VΦ=(2iλ2J+2λQ+iJ(Q2-Qx)-
(2)
其中,
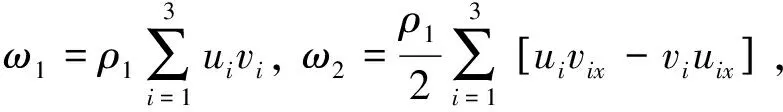
λ为谱参数,Φ=(φ,φ,χ,ψ)T为方程(2)的特征函数。通过相容性条件Ut-Vx+[U,V]=0可以得到方程(1)。
构造Darboux矩阵
T=λI-HΛH-1,
(3)
其中,
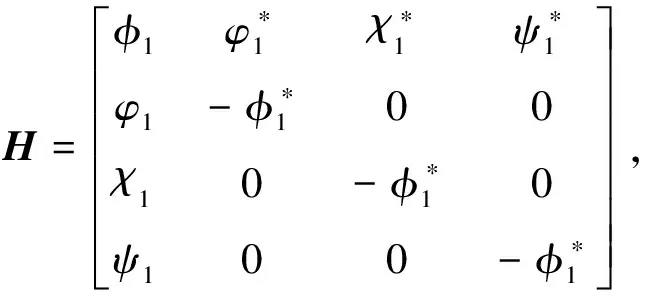
I是一个4×4的单位矩阵,Φ1=(φ1,φ1,χ1,ψ1)T是方程(2)的特征函数。
假设Φ1=Φ1(λ1,η)是方程(2)对应于谱参数λ=λ1(1+η2)的一个特解,η是一个小扰动参数,在η=0处对Φ1进行泰勒展开,有
(4)
其中,
当v1=v1[0],v2=v2[0],v3=v3[0]和λ=λ1时,方程(1)的广义Darboux定义如下:

(5)
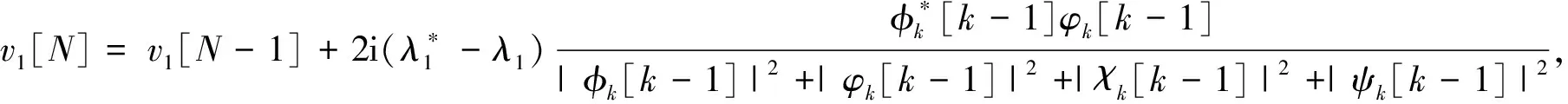
(6)
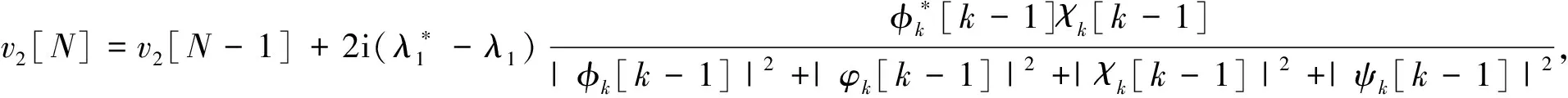
(7)
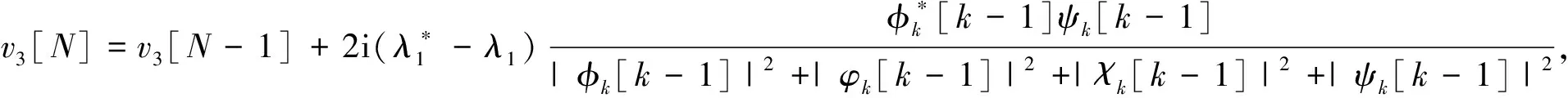
(8)
其中,
T1[k]=λ1I-H1[k-1]Λ1H1[k-1]-1,
Φ1[N-1]=(φ1[N-1],φ1[N-1],χ1[N-1],ψ1[N-1])T,
2 局域波的动力学特性
假设方程(1)的种子解为v1[0]=d1eiθ,v2[0]=d2eiθ,v3[0]=d3eiθ,其中
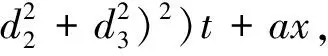
式中:a,d1,d2,d3均为任意实常数。当λ=λ1(1+η2)时,计算得出方程(2)的特解如下:
(9)
其中,
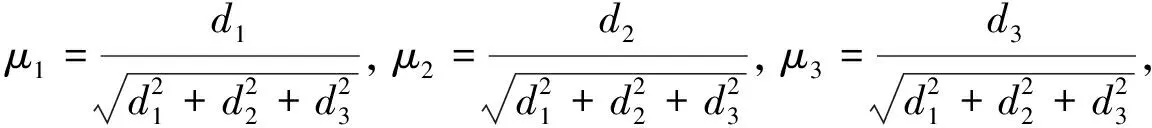

(10)
2.1 一阶局域波
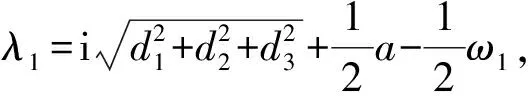

(11)
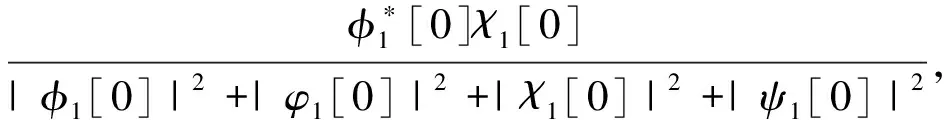
(12)
(13)
v1[1],v2[1],v3[1]的具体表达式较繁琐,此处省略。在其表达式中,包含a,d1,d2,d3,α,β等6个自由参数。
1) 当a=0时,有两种情况:
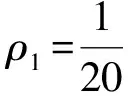
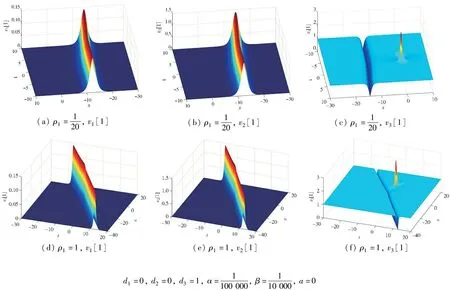
图1 一阶怪波与孤子相互作用的演化图
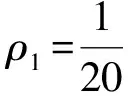
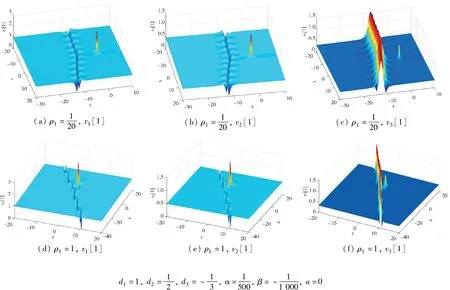
图2 a为0一阶怪波与呼吸子相互作用的演化图
2) 当a≠0且di≠0(i=1,2,3)时,v1[1],v2[1]和v3[1]的一阶局域波如图3 所示,一阶怪波与一列呼吸子相互作用,并且呼吸子的传播方向与t轴的夹角为锐角。

图3 a为时一阶怪波与呼吸子相互作用的演化图
2.2 二阶局域波
考虑如下极限式
(14)
根据方程(6)~(8),得到方程(1)的二阶局域波解
(15)
(16)
(17)
v1[2],v2[2],v3[2]的具体表达式太复杂,此处省略不写。表达式中有8个自由参数a,d1,d2,d3,α,β,m1,n1,下面分情况讨论二阶局域波的动力学行为。
1) 当d1=d2=0,d3=1时,分两种情况讨论:
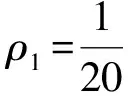
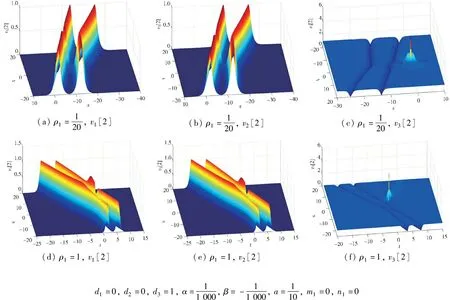
图4 α=, m1=n1=0时二阶怪波与孤子相互作用的演化图
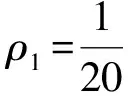
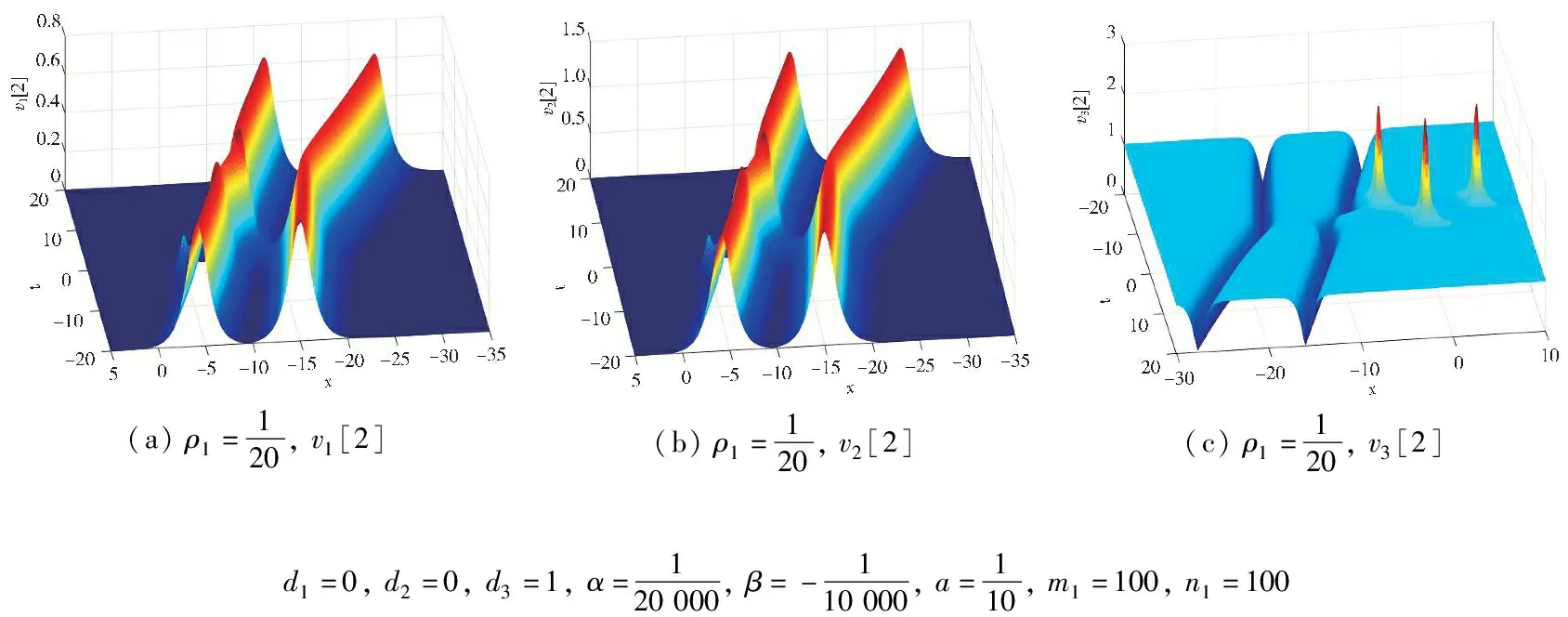
图5 =100时二阶怪波与孤子相互作用的演化图
2) 当di≠0(i=1,2,3)时,v1[2]、v2[2]和v3[2]表现为二阶怪波与两列呼吸子相互作用,且呼吸子呈字母“K”形排列,如图6 所示。若参数m1=30,n1=30,比较图6(a),图6(b),图6(c)和图6(d),图6(e),图6(f)发现,受分离函数Ω(η)的影响,二阶怪波分离成3个一阶怪波且呈三角形排列。
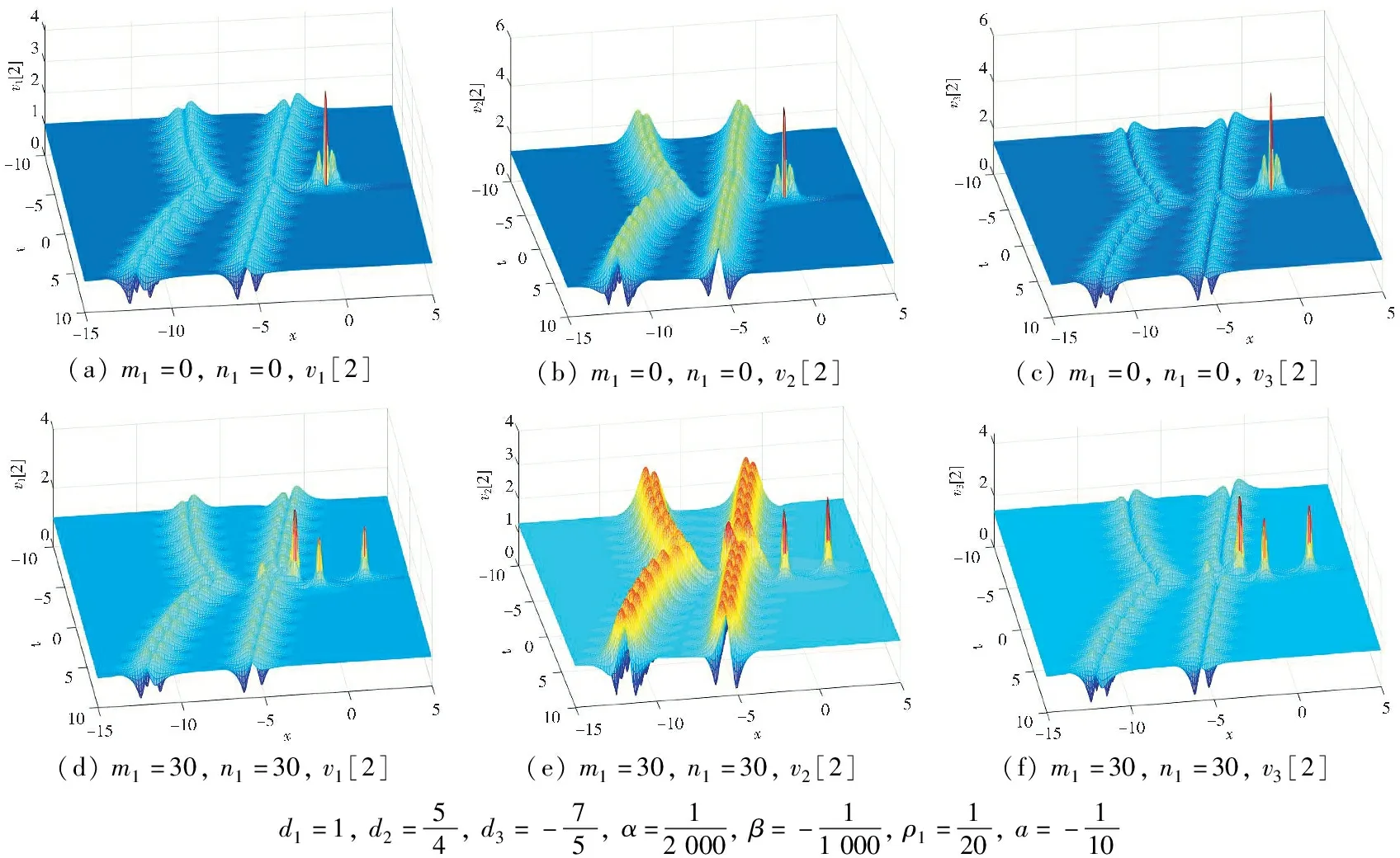
图6 二阶怪波与呼吸子和孤子相互作用的演化图
3 结 论
本文以三分量耦合KE方程为研究对象,选取一组相同指数形式的函数作为方程的种子解,计算得到Lax对方程的特解,然后运用泰勒公式构造方程的广义Darboux变换,得到一阶和二阶局域波解。通过数值模拟,对局域波解中的参数取不同值,分情况研究了3种局域波的相互作用方式,绘制出一阶和二阶局域波形图,进一步分析了其动力学特性。结果表明,在零振幅背景下,怪波与亮孤子相互作用时不容易被发现,与暗孤子和呼吸子相互作用时能被清晰观察。此外,由于分离函数的作用,二阶怪波分离成3个一阶怪波。所得结果对高阶局域波的研究具有一定的理论意义,同时丰富了耦合KE方程的研究。

