改进PM 算法数值求解常微分方程边值问题
谢正荣, 艾轶博, 张卫冬,
(1.北京科技大学国家材料服役安全科学中心,北京 100083;2.华东师范大学数学科学学院,上海 200241)
0 引言
文献[1]利用微分方程残差将常微分方程初值问题的数值求解过程转化为一个优化问题,在梯形数值积分公式的基础上,引入弹性梯度下降法优化参数求得符合精度要求的数值解。本文将其称作PM 算法,该算法基本流程如下:首先在各积分节点处设置二元参数对{wk,bk},独立地线性逼近该节点处的最高阶导函数;随后,从最高阶导函数层开始逐阶向上使用复化梯形求积公式数值积分至解函数层;最后,基于微分方程的残差,迭代优化参数对{wk,bk}。
PM 算法与仅用于求解线性常微分方程初值问题的同类工作[2–3]相比,具有精度高、收敛速度快的优点;而基于循环神经网络的强大逼近能力,PM 算法尤其适用于高阶非线性常微分方程初值问题的数值求解。此外,与文献[4—5]中纯网络型结构的试解相比,PM 方法可严格满足初值条件;而由文献[6]可知,文献[4—5]的方法中,边界误差与域内残差存在竞争关系,故无法严格满足初值条件。
值得注意的是,原始PM 算法虽有上述优势,但它无法解决常微分方程的边值问题:欲启动第k阶梯形求积过程,则需要该阶导函数的初值,即y(k)(x0),否则只能计算各区间内的增量。由于边值问题并不能够提供足够的初值条件,这便导致了此算法无法求解边值问题。以二阶常微分方程两点边值问题I 型边界条件为例

无法完成,进而导致整个求解过程失败。
为将原算法推广至边值问题求解,本文作出如下4 点改进:
1) 提出“分离原理”,使得PM 算法可在一阶常微分方程组形式下使用,从而为PM 算法求解二阶常微分方程两点边值问题提供理论基础。具体地,选取状态量将其转化为一阶常微分方程组,随后基于分离原理分别训练边界误差和域内残差;
2) 在一阶常微分方程组架构中发现了二阶常微分方程I/II 型边值问题在计算格式上的等价性;
3) 在参数集不变的前提下,利用现有参数,保持导数关系,假设缺失的初值条件,结合分离原理,实现PM 算法求解常微分方程I/II 型边值问题,简记为“导数法”;
4) 引入额外参数补充缺失的初值条件,结合分离原理,实现PM 算法求解常微分方程I/II/III 型边值问题和混合型边值问题,以下简记为“增参法”。
最后,通过针对边值问题的数值实验测定了PM 算法的收敛阶(2 阶收敛)。
关注常微分方程两点边值问题数值求解的文献通常仅仅只是针对I 型边界条件展开理论推导、提出对应的专门化的解决方案,例如文献[7—12]。但一般而言,III 型和混合型边值问题的数值求解难度明显大于I 型问题。本文提出的“增参法”是直接面向III 型和混合型边界条件的,且同时兼容I/II 型问题。此外,本文在一阶常微分方程组形式下发现了I/II 型边值问题在计算格式上的等价性,此发现有助于将已有的I 型边界条件处理方式直接应用于II 型问题,提高算法代码复用率。
1 预备知识
原始PM 算法求解单个常微分方程初值问题的基本原理如下。

由于g(xi)和g′(xi)无法直接获得准确值,且不同积分节点处g(xi)和g′(xi)的值不同,即线性主部的斜率和截距随积分节点变化,故考虑为不同积分节点处的线性主部选取不同的可调二元参数对(wi,bi),并通过优化技术不断调整{(wi,bi)}mi=0,以使得
此即为二元参数对(wi,bi)的数学解释。
(ii) 若待求函数仅n阶可导,则(wi,bi)不可作如上理解。但是从积分角度而言,g(x)不够光滑并不影响对其作梯形数值积分,故PM 算法仍然有效。因此,(i)中的解释可看作是“最高阶导函数离散线性参数化”的思想来源。
2 分离原理:改进PM 算法处理边界条件的理论基础
PM 算法求解边值问题时,除需要收敛计算域内各处的微分方程残差外,还需要极小化边界误差,故此时的目标函数将重构为一个多目标优化问题。事实上,将PM 算法应用于一阶常微分方程组初值问题求解时,每一个分量方程都存在一个微分方程残差向量,此时的目标函数同样需要把多个微分方程残差向量同时约束在内。因此,不妨先考虑如何改进原始的PM 算法以求解一阶常微分方程组初值问题,随后便可将相同的原理作用于高阶常微分方程/一阶常微分方程组边值问题求解了。以三元一阶常微分方程组初值问题为例,其一般形式如下

因为目标函数中存在三个误差对应的三个优化项,属于多目标规划。因此,引入λ1、λ2和λ3三个比例系数以表示各个优化项的重要程度。根据文献[13]的推导思路,基于李雅普诺夫稳定性理论易得,原始PM 算法收敛的一个充分性条件为

于是,便将一个多目标规划问题转化为三个相对独立的单目标规划问题加以求解,每一个单目标规划问题即可按照前文的推导方法获得属于自己的独立的自适应学习速率,然后用最速下降法实现极小化。此时权值、偏置值更新规则如下

增量式(11)右边第一项表示基于目标函数J1所作的迭代优化,之后两项以此类推。虽然分离原理告诉我们可以独立地极值化三个目标函数,但由于三个目标函数拥有完全相同的自变量,即所有权值、偏置值,故每一个目标函数都会对所有权值、偏置值作更新。因此,从权值、偏置值角度看,在每一步迭代中,每一个权值、偏置值的增量是所有残差分量引起的多个增量之和。
为强调分离原理本质上仍然是在对所有分量式误差以及可能的边界误差的极小化作综合平衡性考虑,即仍然处理的是多目标规划问题,在后文叙述中常微分方程组的目标函数仍取为等价重构前的加权平方和格式。
现对分离原理的数学本质作出说明:取

其中F=R,D,E,l=1,2,3,则有简化形式

现考虑二阶常微分方程边值问题,只需要将边界误差EBC视作额外增加的又一个微分方程残差分量,即由{R,D}扩张为{R,D,EBC}即可。显然{R,D,EBC}形式上等价于{R,D,E},从而符合上述分离原理范式,故可使用已有的等效学习速率计算公式基于最速下降法同时分别训练域内残差和边界误差。边界误差的权重系数及其在逐次处理方案下的等价形式将在第3 节中详细说明且适用于后文所有求解边值问题的章节内容。
3 改进PM 算法数值求解常微分方程(组)边值问题
以二阶常微分方程为例,边值问题描述为r′′=F(t,r,r′),t ∈[t0,tN]。I 型边界条件r(t0)=α,r(tN)=β;II 型边界条件r′(t0)=α,r′(tN)=β;III 型边界条件
借鉴打靶方法试探性假设缺失的初值,将边值问题转化为初值问题再加以数值求解这一思路,结合PM 算法自身特点,针对性地提出了两种假设初值的方案:保持导数关系假设初值(导数法);引入新参数假设初值(增参法)。转化为初值问题后再用PM 算法求解。
值得注意的是,PM 算法求解边值问题需要额外引入边界误差EBC训练参数调整假设的初值条件。因此,目标函数将由微分方程残差Ri和边界误差EBC两部分组成,二者权重分配参考文献[6,14]分别取λin=1,λBC=10。保证其收敛的自适应学习速率的推导将用到前文提出的分离原理,以分别保证上述两类误差各自收敛最终使得目标函数极小化。为方便,按逐次处理方案进行编程,我们对边值问题目标函数作如下等价变形
这一等价变形适用于下文所有涉及边界误差训练的情况,后文叙述中将省略。
为将II 型边值问题转化为I 型边值问题加以求解,后文所有讨论均在一阶常微分方程组形式中展开,理由详见3.1 节。但需要说明的是,本文提出的导数法与增参法亦可在单个二阶常微分方程形式下作类似推导构造出相应的处理方案。
3.1 二阶常微分方程I/II 型边值问题在一阶常微分方程组形式下的计算格式等价性
对于二阶常微分方程边值问题,I 型边界条件与II 型边界条件在其一阶微分方程组形式下等价。
二阶常微分方程I 型边界问题
令x=r,y=r′,可得如下二元一阶常微分方程组

即
一般形式的二元一阶常微分方程组的I 型边界问题如下
对比式(20)、式(23)和式(24)可知,二阶常微分方程的I 型边界问题的微分方程组形式和二阶常微分方程的II 型边界问题的微分方程组形式均是二元一阶常微分方程组的I 型边界问题的特例,故构造求解二元一阶常微分方程组I 型边界问题的算法即可同时满足求解二阶常微分方程I 型边界问题的和II 型边界问题的需求。所以,对于二阶常微分方程II 型边值问题,首先将其转化为一阶常微分方程组II 型边值问题形式,然后用一阶常微分方程组I 型边值问题的求解算法即可。基于此,后文中我们仅在二元一阶常微分方程组形式下展开讨论。
3.2 导数法求解一阶常微分方程组I/II 型边值问题

以此类推下去。注意,由于只是作近似处理,为避免引入更多的待定参数,故可省去各阶积分常数。按照上述规律类推,可到达0 阶导函数层即解函数层,再令i= 0,即可利用现有参数试探性补充边值问题中缺失的某个初值条件。由于上述类推格式存在逐阶求导关系,故称为导数法。
以二元一阶常微分方程组为例,注意到方程组第二个分量式缺少一个初值条件,不妨假设

1) 计算域内微分方程残差训练
当i=0 时,有

2) 边界误差训练
感兴趣的读者可以尝试在单个二阶常微分方程形式下写出EBC的表达式,并与式(35)做对比可知,将高阶微分方程转换为一阶常微分方程组形式再加以数值求解,往往可以简化计算,得到更为简洁的公式结果。
注意,上述公式表明EBC与第二分量式的参数U和V无关,仅取决于第一分量式的参数W和b,即

算例1 的参数配置见表1 和表2,求解精度见表3。

表1 算例1 导数法改进PM 算法的参数配置

表2 算例1 导数法改进PM 算法的参数配置

表3 算例1 导数法改进PM 算法的求解精度

算例2 的参数配置见表4,求解精度见表5。

表4 算例2 导数法改进PM 算法的参数配置

表5 算例2 导数法改进PM 算法的求解精度
3.3 引入独立参数试探初值条件
引入新参数假设初值,新参数相当于扩充微分方程残差的自变量维度,对于二阶常微分方程即有
因此,对于计算域内微分方程残差的训练,只需额外求解与新引入参数相关的梯度。然后,相应地对引入新参数前的等效学习速率公式补充相关项,即可沿用求解初值问题的程序代码。
与保持导数关系假设初值条件方法相比较,引入与旧参数集{w,b}无关的、独立的参数p和q补充初值条件,可以避免引入二次项增加公式复杂度和计算量,本文称此方法为增参法。
3.3.1 增参法求解一阶常微分方程组I/II 型边值问题
对于如下二元一阶常微分方程组

权值偏置值的更新规则如下
1) 计算域内微分方程的残差训练
基于分离原理,易得计算域内各分量式的自适应学习速率
所以,与常微分方程组初值问题中的G1和G2相比较,有如下关系
其中G1和G2参见式(32)和式(33),即引入独立参数试探初值条件方案中的域内残差与3.2 节的第1)小节中保持导数关系假设初值条件方案中的域内残差是一致的。于是,有
基于此,在二元一阶常微分方程组初值问题求解程序中,补充相关梯度、修正自适应学习速率后,即可直接用来求解二元一阶常微分方程组边值问题。
2) 边界误差训练
注意,上述公式表明,新引入的参数p和q不参与EBC的计算,且EBC与第二分量式的参数U和V无关,仅取决于第一分量式的参数W和b,即EBC=EBC(W,b)。由于分量式是一阶微分方程,所以计算EBC只需经过一次梯形求积分。这再一次表明,数值求解时,将高阶常微分方程转化为一阶常微分方程组再进行求解会更加简洁。
基于此,易知引入新参数试探初值条件方案中的∂EBC/∂W和∂EBC/∂b与保持导数关系试探初值条件方案中的∂EBC/∂W和∂EBC/∂b完全一致,从而边界处自适应学习速率计算公式亦保持一致,故此处不再赘述,所需梯度值及边界处自适应学习速率详见3.2 节中第2)小节。
算例3 悬链线方程[15]
I 型边界条件y(0)=1,y(5)=3.282 557。以Matlab 的bvp4c 命令所得数值解为参考。
设u=y,v=y′,则有
算例3 的参数配置如表6,分量式权重和边界误差权重见表7,表8 给出了求解精度。

表6 算例3 增参法改进PM 算法的参数配置

表7 算例3 增参法改进PM 算法的分量式权重和边界误差权重

表8 算例3 增参法改进PM 算法的求解精度
算例4[16]r′′=-r+2r′+t,t ∈[-2,1]。II 型边界条件r′(-2)=0.594,r′(1)=1。解析解r=(t-2)et+t+2。
取u=r,v=r′,一阶常微分方程组形式为

算例4 的参数配置见表9,求解精度见表10。

表9 算例4 增参法改进PM 算法的参数配置

表10 算例4 增参法改进PM 算法的求解精度
3.3.2 增参法求解一阶常微分方程组III 型边值问题
对于如下的二元一阶常微分方程组

1) 计算域内微分方程残差训练
记
算例5 的参数配置见表11,求解精度见表12,求解结果如图1 所示。

图1 算例5 增参法改进PM 算法的求解结果

表11 算例5 增参法改进PM 算法的参数配置
3.3.3 增参法求解一阶常微分方程组混合型边值问题
设有二阶常微分方程r′′=φ(t,r,r′),t ∈[t0,tN]。三类边界条件的统一形式如下
其中α0α1≥0,β0β1≥0。
对于二元一阶常微分方程组,则有
其中α0α1≥0,β0β1≥0。
易知,当α0=β0= 0 且α1̸= 0,β1̸= 0 时,即为I 型边值条件,当α1=β1=0 且α0̸= 0,β0̸= 0 时,即为II 型边值条件,当α1=β1= 1 且α0> 0,β0> 0 时,即为III 型边值条件。
当然,两端点处的边值条件可以是不同类型。例如:当α1̸= 0,α0= 0,β1=0,β0̸=0 时,t=t0处则为I 型边值条件,t=tN处则为II 型边值条件。如此,便是一个混合型边值问题。
记x(t)和y(t)为微分方程组的真实解。xt(t)和yt(t)为PM 算法所求得的微分方程组的近似解。xt(ti)和yt(ti)简记为xi和yi。x′(ti)的近似值x′t(ti),简记为x′i,设x′i=wixi+bi,i= 0,1,···,N。y′(ti)的近似值y′t(ti),简记为y′i,设y′i=uixi+vi,i=0,1,···,N。
记W= [w0,w1,···,wk,···,wN]T,b= [b0,b1,···,bk,···,bN]T,U= [u0,u1,···,uk,···,uN]T,V= [v0,v1,···,vk,···,vN]T。注意方程组第缺少x(t0)和y(t0)两个初值条件,设

其中θ=W,b,U,V,µ,τ,p,q。
1) 计算域内微分方程残差训练
记

同理可得
2) 边界误差训练
算例6r′′=-r+2r′+t,t ∈[-1,1]。混合边界条件如下,当t=-1 时,II 型边界条件-r′(-1) =-0.264 24。当t= 1 时,III 型边界条件r(1)+r′(1) = 1.281 7。解析解r=(t-2)et+t+2。
取x=r,y=r′,一阶常微分方程组形式为
算例6 的参数配置见表13,求解精度见表14,求解结果如图2 所示。

图2 算例6 增参法改进PM 算法(逐点配置η)的求解结果

表13 算例6 增参法改进PM 算法的参数配置

表14 算例6 增参法改进PM算法的求解结果
4 PM 算法的收敛阶
采用文献[12]的做法,通过针对边值问题的数值实验来比较本文PM 算法与传统的迎风格式和中心差分格式的收敛阶
微分方程
I 型边界条件u(0)=0,u(1)=0,解析解u=sin(πt)。
取x=u,y=u′,一阶常微分方程组形式为
边界条件处理方案选用3.3 节中的增参法。迭代精度10-10,允许最大训练次数5 500,分量式与边界误差权重λ1=λ2= 1/2,λBC= 10。收敛阶的实验结果见表15。
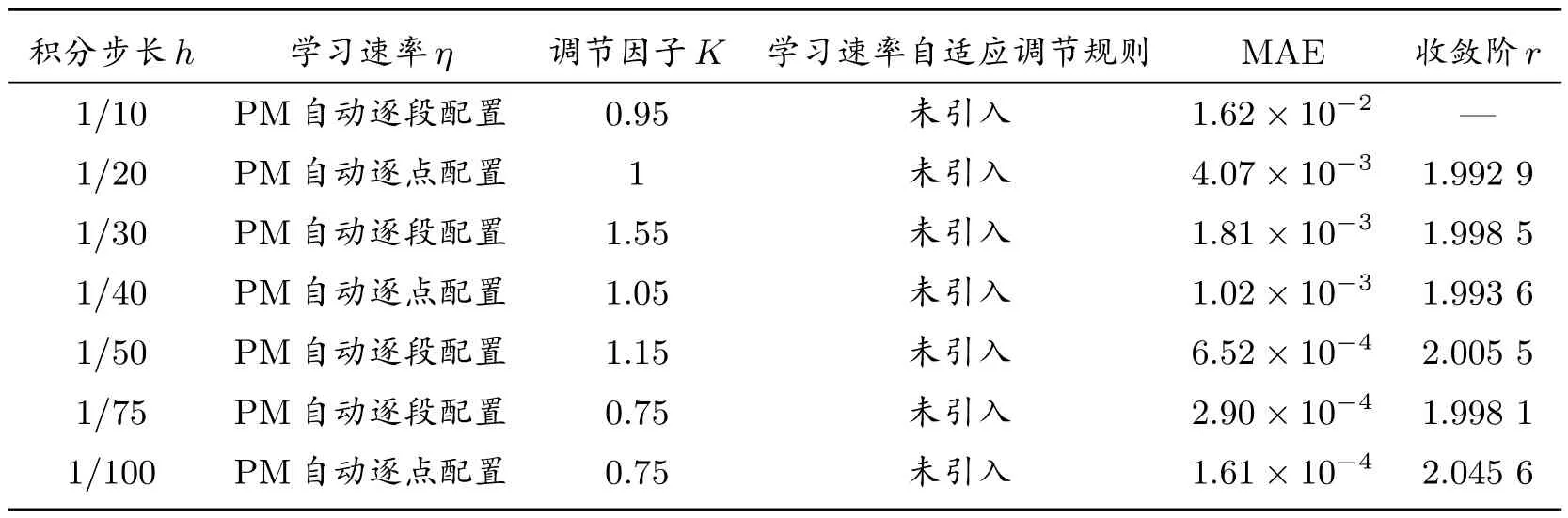
表15 PM 算法的收敛阶
已知迎风格式是1 阶收敛,中心差分格式是2 阶收敛,本文改进的PM 算法收敛阶为2 阶。
5 总结
本文首先介绍了现有文献中PM 算法的基本原理和计算过程,随后考虑到将高阶常微分方程转化为一阶常微分方程组进行求解是传统递推型数值解法的常规预处理方式,有利于计算的范式化和推广,故为在常微分方程组形式下使用PM 算法,提出分离原理将微分方程组对应的多目标优化问题转化为多个相对独立的单目标优化问题。PM 算法的前向计算过程依赖于复化梯形求积公式的递推型数值解法,因此在求解初值条件缺失的两点边值问题时该算法失效。为将该算法推广至边值问题求解,借鉴试射法的思想,结合PM 算法的特点,提出了保持导数关系试探初值条件和引入独立参数试探初值条件两种解决方案,并基于提出的分离原理引入边界误差训练,这两种方法在求解边值问题时均取得了较好的效果;最后,通过针对边值问题的数值实验测得改进后的PM 算法的收敛阶为2 阶。

