Banach 空间中复合刚性Volterra泛函微分方程隐显Euler 方法的稳定性分析
龙 滔, 余越昕
(湘潭大学数学与计算科学学院,湘潭 411105)
0 引言
近年来,刚性Volterra 泛函微分方程初值问题数值方法的研究得到了众多学者的高度关注,取得了大量研究成果[1–10]。对于复合刚性微分方程,由于问题可分解成刚性部分和非刚性部分,自然的想法是用隐式方法求解刚性部分,显式方法求解非刚性部分,从而达到提高计算效率的目的。对于各种复合刚性问题隐显方法的研究可参见文献[11—15]。对于复合刚性Volterra 泛函微分方程,Li[16]给出了求解问题的正则Euler 分裂方法,研究了方法的稳定性和收敛性。应当指出,上述研究成果大都是在内积空间中基于单边Lipschitz 条件获得的。然而对于某些刚性问题,其单边Lipschitz 常数却不可避免地取非常巨大的正值。因此,有必要突破内积空间和单边Lipschitz 常数的限制,直接在Banach 空间中研究数值方法的相关结论。鉴于此,本文将隐显Euler 方法用于求解Banach 空间中一类非线性复合刚性Volterra 泛函微分方程。
1 求解问题的隐显Euler 方法
设X是实或复的Banach 空间,//·//为其范数,对于任意给定的时间间隔I ⊂R,定义符号CX(I)表示由所有连续映射x:I-→X构成的Banach 空间,其中范数//x//∞=maxt∈I //x(t)//。考虑如下初值问题
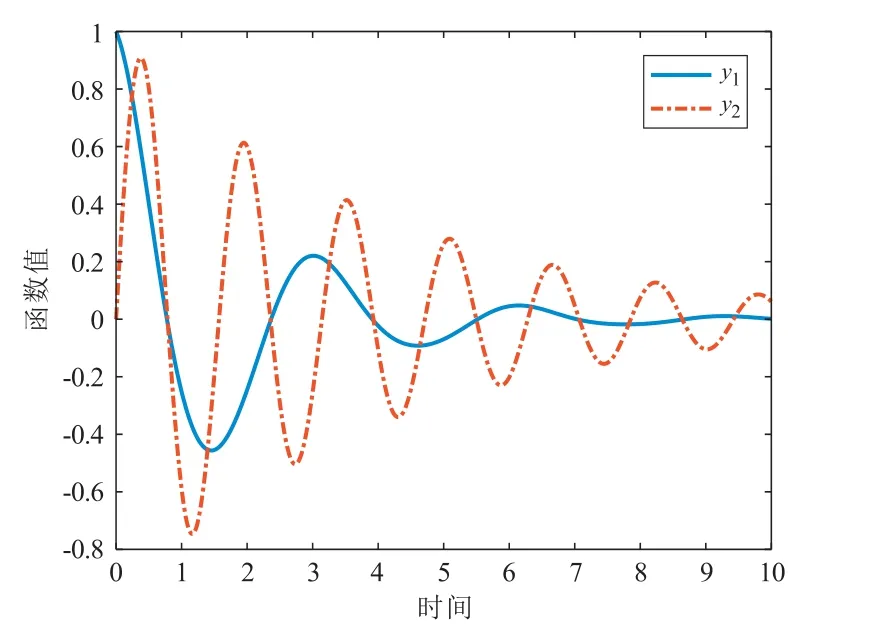
其中a、b、τ是常数,-∞ α1、α2、β1和β2是适度大小的实常数,并且函数µ1(t)和µ2(t)满足 参考文献[17],定义 为了描述方便,我们把满足条件(3)∼(6)的所有问题(1)记作问题类D(α1,α2,β1,β2,µ1,µ2)。另外,若问题(1)中的积分区间[a,b]变成[a,+∞)且也满足条件(3)∼(6),则我们把这类问题记作问题类¯D(α1,α2,β1,β2,µ1,µ2)。 将隐式Euler 和显式Euler 分别应用于问题(1)中的f1(t,y(t),y(·))和f2(t,y(t),y(·)),得到求解问题(1)的隐显Euler 方法 其中插值函数yh(t)表示真解y(t)在区间[a-τ,tn+1]上的近似值,yn是真解y(tn)的逼近,hn=tn+1-tn是给定的步长。记时间网格∆h:={t0,t1,···,tN}且满足a=t0 为了分析隐显Euler 方法的稳定性,我们引入问题(1)的扰动问题 定理1 假设问题(1)属于问题类D(α1,α2,β1,β2,µ1,µ2),设yn和zn是隐显Euler 方法求解问题(1)及其扰动问题(12)得到的数值解序列,则有 由此完成定理1 的证明。 定理2 假设问题(1)属于问题类D(α1,α2,β1,β2,µ1,µ2),设yn和zn是隐显Euler 方法求解问题(1)及其扰动问题(12)得到的数值解序列,记 由此我们很容易获得以下定理。 定理3 假设问题(1)属于问题类D(α1,α2,β1,β2,µ1,µ2),设yn和zn是隐显Euler 方法求解问题(1)及其扰动问题(12)得到的数值解序列,且α1+α2+2(β1+β2)<0,则有 在本节,我们将给出隐显Euler 方法的渐近稳定性结果。 这里ξk=tnk,ξ0=t0=a,n0= 0。由于hn ≤µ(0)1,对于nk ≤n ≤nk+1-1,根据定理1,我们有 且满足0< ˜Cµ<1。因此,类似定理4 的证明,我们很容易获得以下定理。 定理5 假设问题(1)属于问题类¯D(α1,α2,β1,β2,µ1,µ2),设yn和zn是隐显Euler 方法求解问题(1)及其扰动问题(12)得到的数值解序列,且˜h=infn≥0{hn}>0,当 例1 考虑如下非线性刚性初值问题 故由定理3 和定理5 知,问题(44)在区间[0,10]和[0,+∞)分别是稳定的和渐近稳定的。 我们将用隐显Euler 方法(9)和(10)以及全隐Euler 方法[17] 分别表示数值解yn与真解y(tn) 的误差和计算阶,E(h) :=//yn-zn//1表示问题(1)和扰动问题(12)的误差。 取h= 0.01,将方法(9)和(10)以及全隐Euler 方法(45)分别应用于问题(44),其数值解如图1 和图2 所示。从图1 和图2 可以看出,方法(9)和(10)与全隐Euler 方法(45)图形基本一致。 图2 全隐Euler 方法(45) 取h=1/N(N=400,800,1 600,3 200),将方法(9)和(10)以及全隐Euler 方法(45)分别应用于问题(44),结果见表1。从表1 可以看出,方法(9)和(10)与全隐Euler 方法(45)在同一步长下,其误差相当,且都是1 阶收敛。而方法(9)和(10)的CPU 时间低于全隐Euler 方法(45),从而说明方法(9)和(10)较方法(45)能够降低计算成本。 表1 当t=10 时,方法(9)和(10)以及方法(45)求解问题(44)的误差 给出问题(44)的扰动值 取h=0.01,其误差E(h)如图3 所示。从图3 可以看出,方法(9)和(10)是渐近稳定的,从而说明本文所给结论的正确性。 图3 h=0.01,问题(44)的误差E(h) 在本文,针对Banach 空间中复合刚性Volterra 泛函微分方程,将隐式Euler 用于问题刚性部分的求解,显式Euler 用于非刚性部分的求解,得到了求解问题的隐显Euler 方法。给出了方法的稳定性及渐近稳定性条件,最后的数值试验结果显示隐显Euler 方法(9)和(10)比全隐式Euler 方法(44)能够大幅度提高计算效率,从而表明隐显方法求解复合刚性问题时,有较好的稳定性和较高的计算效率。
2 隐显Euler 方法的稳定性分析
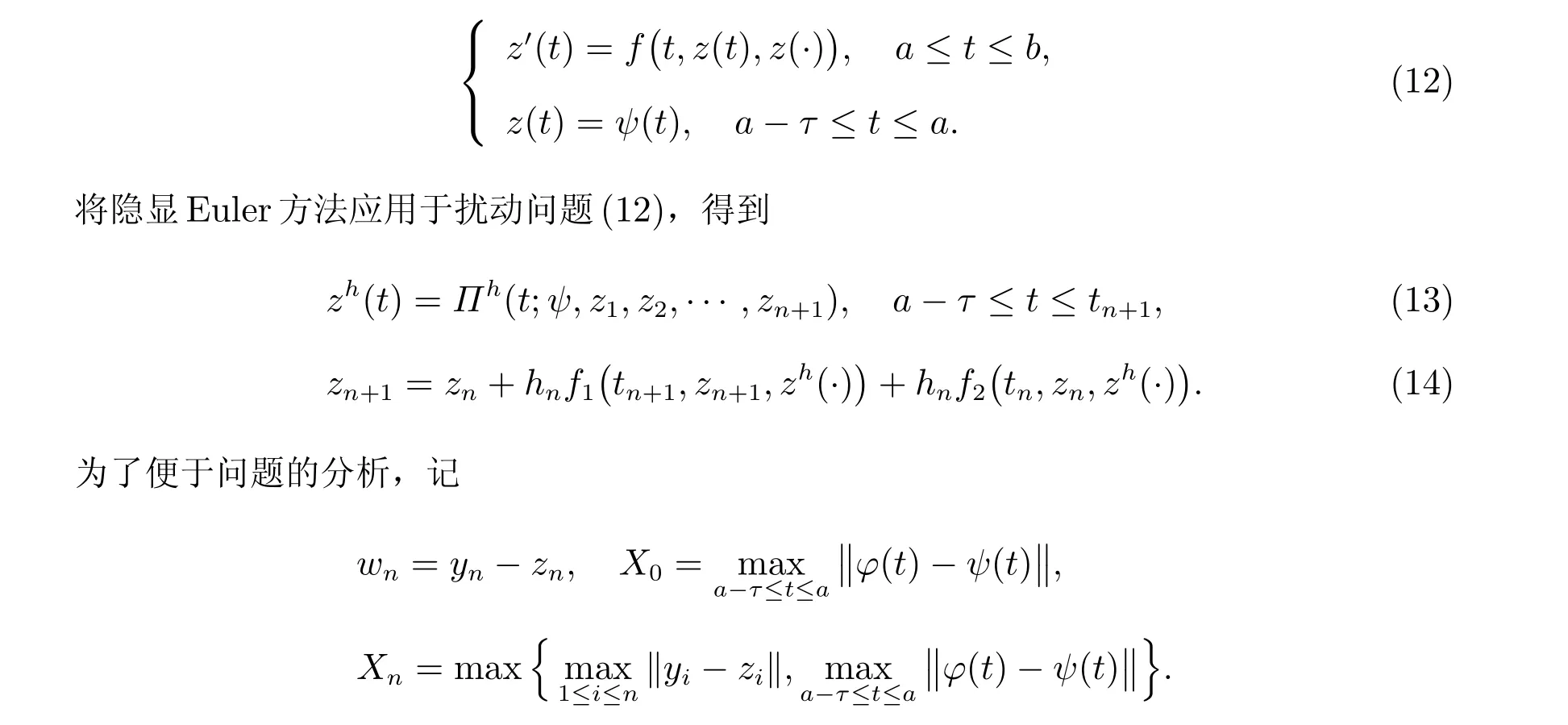
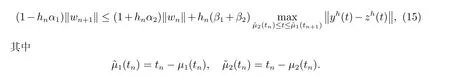
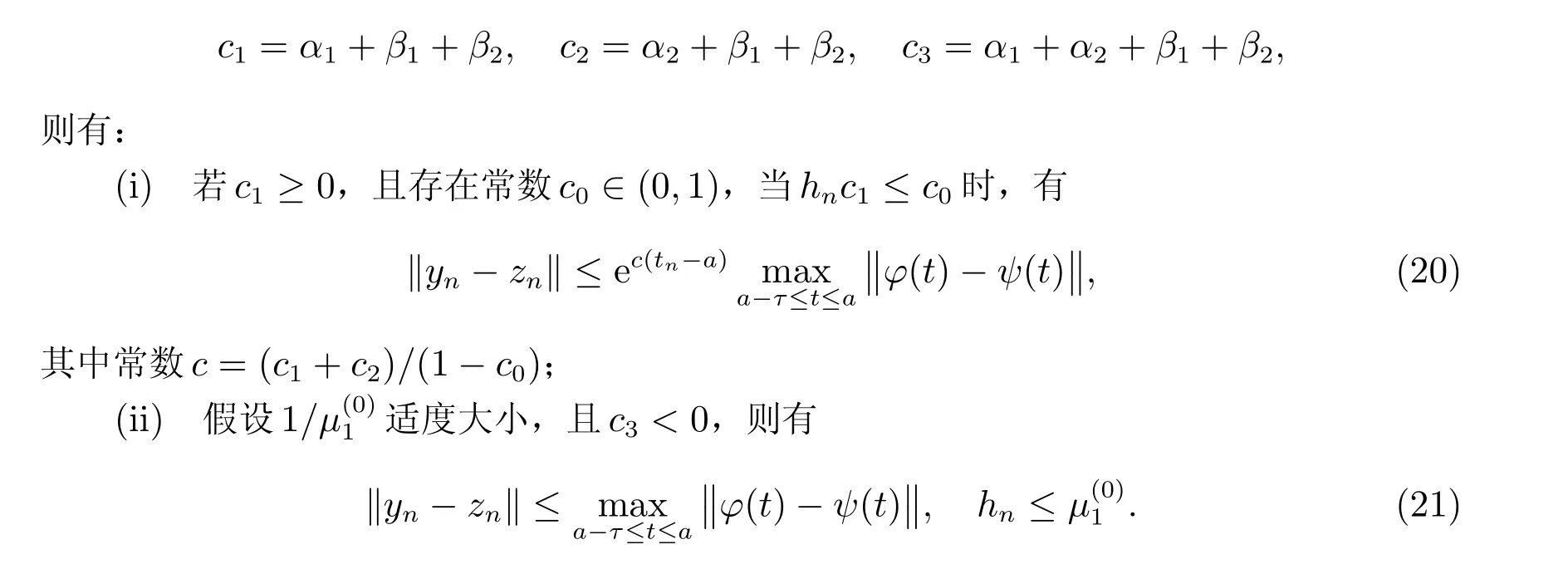
3 隐显Euler 方法的渐近稳定性分析
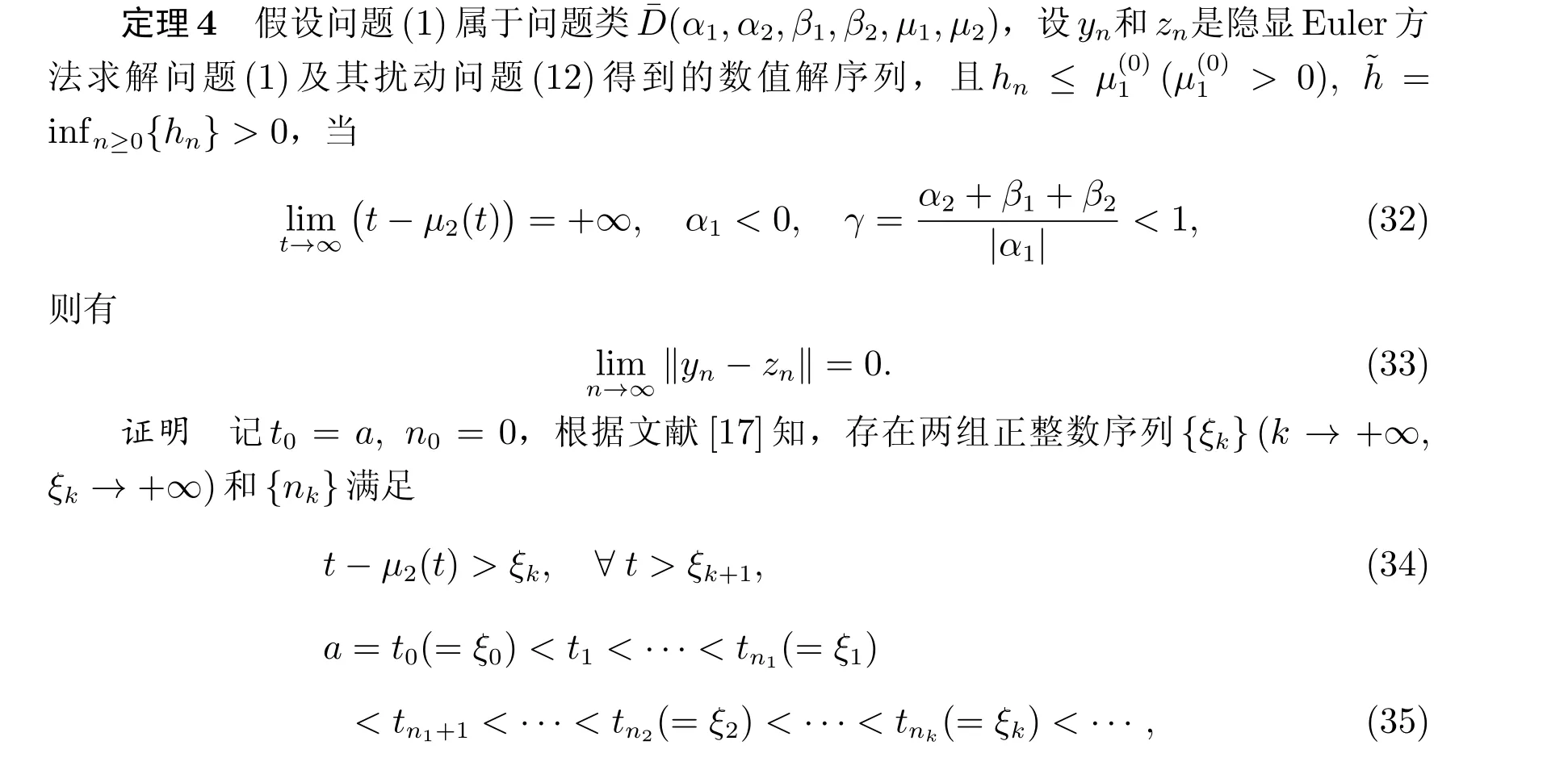

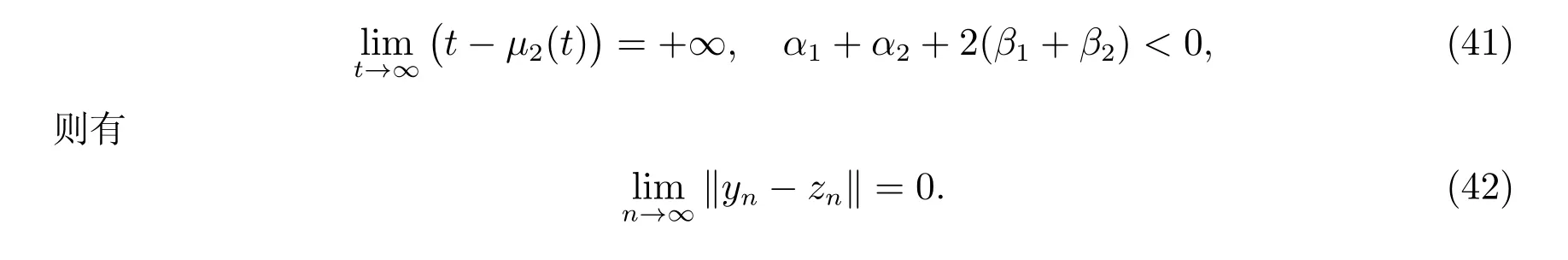
4 数值试验




5 结论

