新型布谷鸟搜索算法及其应用

覃国锐

(广西科技师范学院，广西 来宾 546199)

0 引言

布谷鸟搜索(Cuckoo Search, CS)算法[1]由于其迭代公式简单、参数调节少、寻优能力强等特点，自提出后迅速在各个领域得到了成功应用。但该算法和其他群智能算法一样存在收敛速度慢和计算精度不高等缺点，对此一些学者提出了各种改进方法及应用。文献[2]提出一种改进的分数阶布谷鸟搜索算法，通过在莱维飞行中引入分数阶差分，并对历史信息加以利用，提高了算法的局部搜索能力。文献[3–4]通过改进发现概率和步长的自适应调整来提高算法性能。文献[5]通过修改局部搜索位置更新公式，然后将种群一分为二，较优种群和较差种群分别按不同的更新公式进行迭代来增强算法的局部搜索能力。文献[6]对CS 算法中的步长控制量和淘汰概率进行优化调整，并对水质监测无线传感器部署进行优化。文献[7]提出基于逐维反向学习的动态自适应布谷鸟算法，首先对解进行逐维反向学习，然后使用精英保留方式和缩放因子提升算法活力。文献[8]提出分段加权布谷鸟算法及其应用，通过引入自适应步长控制量和相应的分段加权位置更新公式来改进算法。文献[9]提出改进的布谷鸟MT 反演算法，引入粒子群算法中的全局最优解加强算法的局部勘测能力。文献[10]提出基于改进布谷鸟算法的PID 控制器整定新方法，首先运用t分布随机序列初始化种群，然后将布谷鸟算法和非线性随机直接算法结合，提升了全局搜索性能。文献[11]提出动态调整概率的双重布谷鸟搜索算法，在发现概率中引入分布熵及采用新型步长因子与莱维飞行构成双重搜索模式，寻优性能明显提升。文献[12]提出基于局部搜索增强策略的自适应反向学习布谷鸟算法，采用反向学习扰动机制和自适应发现概率提高算法的收敛速度及解的质量。文献[13]提出基于改进布谷鸟搜索(Improved Cuckoo Search, ICS)算法的圆度误差评定，引入轮盘赌选择方法，对CS 中的莱维飞行步长缩放因子及重新寻窝概率进行优化，精度和收敛速度优于基本CS 算法。文献[14]提出多物种布谷鸟搜索算法，旨在模拟多个布谷鸟竞争生存的物种来验证该算法的有效性。

上述算法从不同角度提高了CS 算法性能，本文进一步利用信息分享、局部增强算子和新方式建立鸟巢来提高种群多样性、局部勘探能力和收敛速度。通过15 个基准函数和2 个图像配准问题对算法性能进行评测，验证了所提算法的有效性。

1 算法介绍

1.1 布谷鸟搜索算法

布谷鸟搜索算法是利用莱维飞行特性来模拟布谷鸟寻窝产卵的行为求解优化问题。寻窝产卵的位置i的更新公式为

其中xti表示第i个鸟巢在第t代的位置，n表示种群规模数目，a0为常数，通常取值为0.01，L´evy 表示莱维飞行，best 为当前最优位置，“·”表示点乘。若宿主发现外来鸟蛋时，则以pa ∈[0,1]的概率丢弃鸟巢，然后以

的方式建立新巢，其中x表示整个鸟巢，r ∈[0,1]为服从均匀分布的随机数，xtg和xtk表示第t代种群随机的两个位置。莱维飞行是一个带重尾的随机游走，以小步长聚集和偶尔大步长跳跃，这种方式有利于算法跳出局部最优。莱维飞行的数学表达式如下

其中Γ为伽马函数，µ和ν是相互独立的随机变量，服从均值为0，方差为1 的正态分布，β ∈[1,2]为常数。

1.2 ICS 算法

本文利用信息分享、局部增强算子和新方式建立鸟巢来改进基本的布谷鸟搜索算法。

1.2.1 信息分享

在CS 中，通过式(1)进行莱维飞行搜索，其计算过程先求出第i个个体位置与最优位置的差值然后再作用于第i个个体位置，这种相似行为的计算方式如文献[15]所述，可能会导致搜索空间多样性的丧失。因此，如果个体陷入局部最优值，则无法逃脱。在这种情况下，ICS 算法必须采用新机制增强勘探能力，跳出局部最优。该机制的核心思想是通过交换群内不同位置的信息来提高种群多样性和利用正余弦函数的周期性和振荡性趋于全局最优。具体操作如下：首先，从整个鸟巢随机选取3 个个体，如x(p1)、x(p2)、x(p3)，其中每一个p都是由randperm(n)函数随机生成，n表示种群规模；然后，通过

对每一个个体进行重组，在重组过程中加入正余弦函数以增强解的搜索空间，使其邻域搜索更加高效。其中maxiter 为最大迭代次数，r ∈[0,1]为随机数，其他参数含义与式(1)相同。其目的换替代式(1)。

1.2.2 局部增强算子

在CS 中，其核心思想是通过莱维飞行搜索最优解。由于莱维飞行是多数小步长聚集和偶尔大步长跳跃，这种方式虽然有利于跳出局部最优，但搜索的精度完全由小步长聚集来确定，显然这是基本布谷鸟搜索算法精度不高和收敛速度慢的主要原因。针对这一不足，本文引入局部增强算子，将式(1)进行修改，并使用随迭代次数变化公式，使其在迭代初期搜索范围较广，而迭代后期搜索范围较窄，然后再在最优值附近进行搜索，其计算公式如下

其中r1,r2∈[0,1]为随机数。

1.2.3 新方式建立鸟巢

在CS 中，以式(2)方式建立新鸟巢，虽然在一定程序上增加了新鸟巢位置的可能性，但未保留当前种群最优位置，使得搜索效率低下。因此，本文将式(2)重新定义为如下公式

1.3 ICS 算法实施步骤

基于上述3 个层面的改进，新算法可表述如下：

步骤1 设置种群规模、最大迭代次数和问题边界，并在边界范围内随机初始化鸟巢，求出最优值和最优解；

步骤2 判断是否达到最大迭代次数，如果是，输出最优值和最优解，否则进入步骤3；

步骤3 按照式(5)计算b，对每一个鸟巢判断随机数r，如果r ≤0.5，那么执行式(8)∼(10)，否则执行式(6)∼(7)，并越界处理与计算此时鸟巢的最优值，如果较之前的优越，则更新最优值和鸟巢；

步骤4 产生一个随机数，若大于pa，则执行式(11)，对种群中每一个新鸟巢进行越界处理，计算此时鸟巢的最优值，如果较之前的优越，则更新最优值和鸟巢；

步骤5 判断此时的最优值，若较步骤1 中的最优值优越，则替换最优值和最优解。迭代次数加1，跳转步骤2。

1.4 ICS 算法时间复杂度分析

算法的种群规模为n，最大迭代次数为maxiter，搜索空间维数为dim，CS 算法的时间复杂度为O(n×maxiter×dim)，而ICS 算法在莱维飞行的寻优过程中只是以一定概率执行式(5)∼(9)，并未增加CS 算法的时间复杂度。

2 仿真实验及比较

为了验证本文所提出ICS 算法的性能，选取15 个基准函数进行测试，如表1 所示，并与基本的CS 算法、GWO 算法[16]和SSA 算法[17]进行性能比较，比较结果如表2 所示。算法的参数设置为：种群规模为30，最大迭代次数为500，pa= 0.25，每种算法独立运行30 次，所有结果均为30 次实验的平均值和标准差，加粗字体表示与其他算法比较时求解的最优值，实验环境为Windows 10，在Matlab 2016a 软件中编程实现。从表2 可知，对函数f12而言，ICS 算法求解的平均值和方差比CS 算法稍差，对函数f11而言，ICS 算法求解效果与CS 算法和SSA 算法一致，但优于GWO 算法。对函数f13、f14和f15，ICS 算法求解的平均值虽然与CS 算法一致，但方差优于它，且平均值和方差均优于GWO 算法和SSA 算法。其余10 个函数ICS 算法求解的结果均优于CS 算法、GWO 算法和SSA 算法；尤其对函数f1、f5、f6、f8、f9，f11、f13、f14和f15，ICS算法求解结果达到理论最优值，而未达到理论最优值的函数f2、f3、f4、f7、f10，ICS 算法求解精度比CS 算法、GWO 算法和SSA 算法提高了几个到几百个数量级不等。值得一提的是，对函数f5，其理论最优值位于一条狭长的山谷中，众多算法难以获得其全局最优，但本文算法获取了理论最优值，可见ICS 算法的优越性。

表1 基准函数

表2 ICS 算法与其它算法的比较结果

图1 展示了4 种算法对部分基准函数的寻优曲线(随机选取一次)。从图1 可知，ICS 算法的收敛速度和计算精度较其他3 种算法优越。显然，ICS 算法具有更快的收敛速度和更高的计算精度。

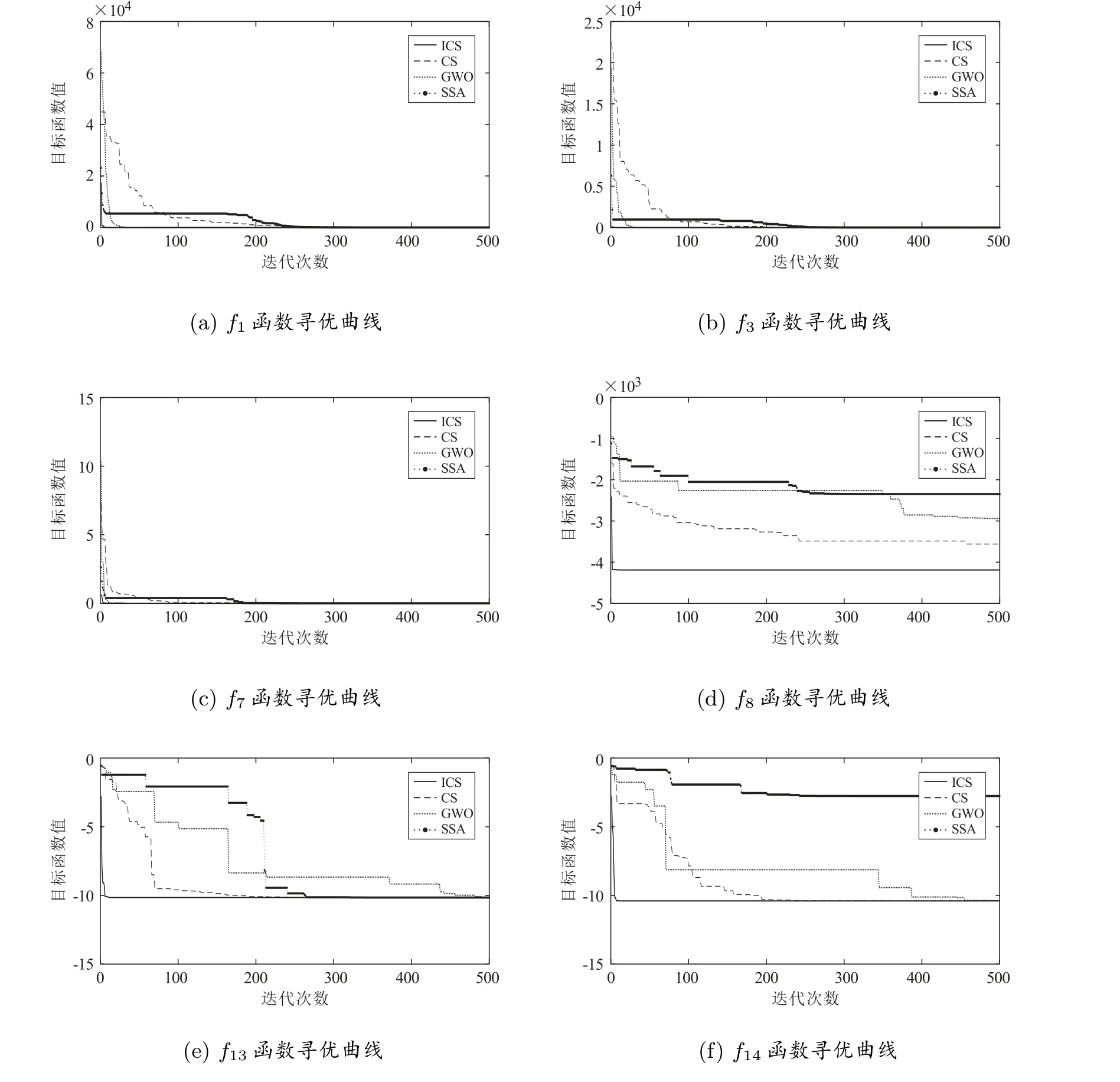
图1 部分函数的收敛曲线

进而，我们将本文ICS 算法与其它改进算法进行比较，结果如表3 所示，表中“—”表示相关算法未对相应函数进行测试。由表3 可知，与文献[3]的APCS 算法比较，仅函数f9结果ICS 算法结果一致，其余4 个函数结果均次于ICS 算法，且其迭代次数为600。与文献[18]的LECUSSA 算法比较可知，仅函数f12结果优于ICS 算法，其余14 个函数结果均次于ICS 算法。与文献[19]的RCSSA 算法比较可知，仅函数f3结果优于ICS 算法，函数f1、f9和f10测试结果与其相同，其余11 个函数测试结果均次于ICS 算法。与文献[20]的CGSSA 算法比较可知，仅函数f7和f13结果优于ICS 算法，函数f6、f9和f10测试结果与其相同，其余10 个函数测试结果均次于ICS 算法。因此，本文所提出的ICS 算法无论与基本算法相比，还是其他改进算法相比，都具有显著的优势。

表3 ICS 算法与相关改进算法的比较结果

3 ICS 算法在医学图像配准中的应用

3.1 互信息图像配准

在图像配准过程中，坐标、角度和大小保持不变的图像称为参考图像，记为R，待配准的图像称为浮动图像，记为F。设R(i,j)和F(i,j)分别表示参考图像和浮动图像的灰度值。令(x,y)表示浮动图像在横坐标和纵坐标的位移，(u,v)表示浮动图像中心的坐标，θ表示浮动图像的旋转角度，T表示作用在浮动图像上的仿射变换，可以表示为

对参考图像和浮动图像进行配准，实质上是求解最佳的几何变换T，使得其互信息最大。基于最大互信息的图像配准无需对图像进行分割和特征点的提取，互信息(Mutual Information, MI)是信息论中描述两个系统之间相关性的度量函数。图像配准的互信息可以定义为两幅图像间的相似程度，参考图像的熵表示为

其中N表示图像的总像素点数，pi表示灰度值为i的像素点数。图像R和F的联合熵表示为

其中pRF(r,f)是随机变量R和F的联合概率分布函数。图像R和F的互信息表示为

互信息未解决图像重叠区域的影响，而归一化互信息(Normalized Mutual Information, NMI)的配准结果更加准确和稳定。因此，本文采用

作为图像配准的目标函数。

3.2 仿真实验与结果分析

实验1 选用MRI 脑部横断面图像(257×221)进行配准实验。如图2 所示，图2(a)为参考图像，图2(b)是将参考图像水平、垂直方向分别移动13 个和7 个像素，绕中心旋转10◦得到的浮动图像。由于智能算法的不稳定性，每个算法独立运行30 次，最优配准参数的效果图如图2(c)所示；30 次平均配准参数计算结果如表4 所示；4 种算法平均NMI 值进化曲线比较图如图2(d)所示。通过观察图2(c)中4 种算法的MRI 图像配准结果图，难以分辨其优劣，但从表4 的定量结果可知：ICS 算法的Delta 值最小，而NMI 值最大；且就Delta 值和NMI 值而言，ICS 算法优于其他算法；就运行时间而言，ICS 算法小于CS 算法，但大于GWO 算法和SSA 算法，可见ICS 算法运行较慢，在没有增加算法复杂度的情况下，ICS 算法的运行效率略有提升。另外，从图2(d)的4 种算法NMI 值进化曲线比较图可知：ICS 算法收敛速度最快、精度更高，基本上在15 代以内达到了全局最优解；且明显优于GWO 算法、SSA 算法和CS 算法，这充分说明改进后的ICS 算法在全局搜索和局部搜索能力方面得到了改善。

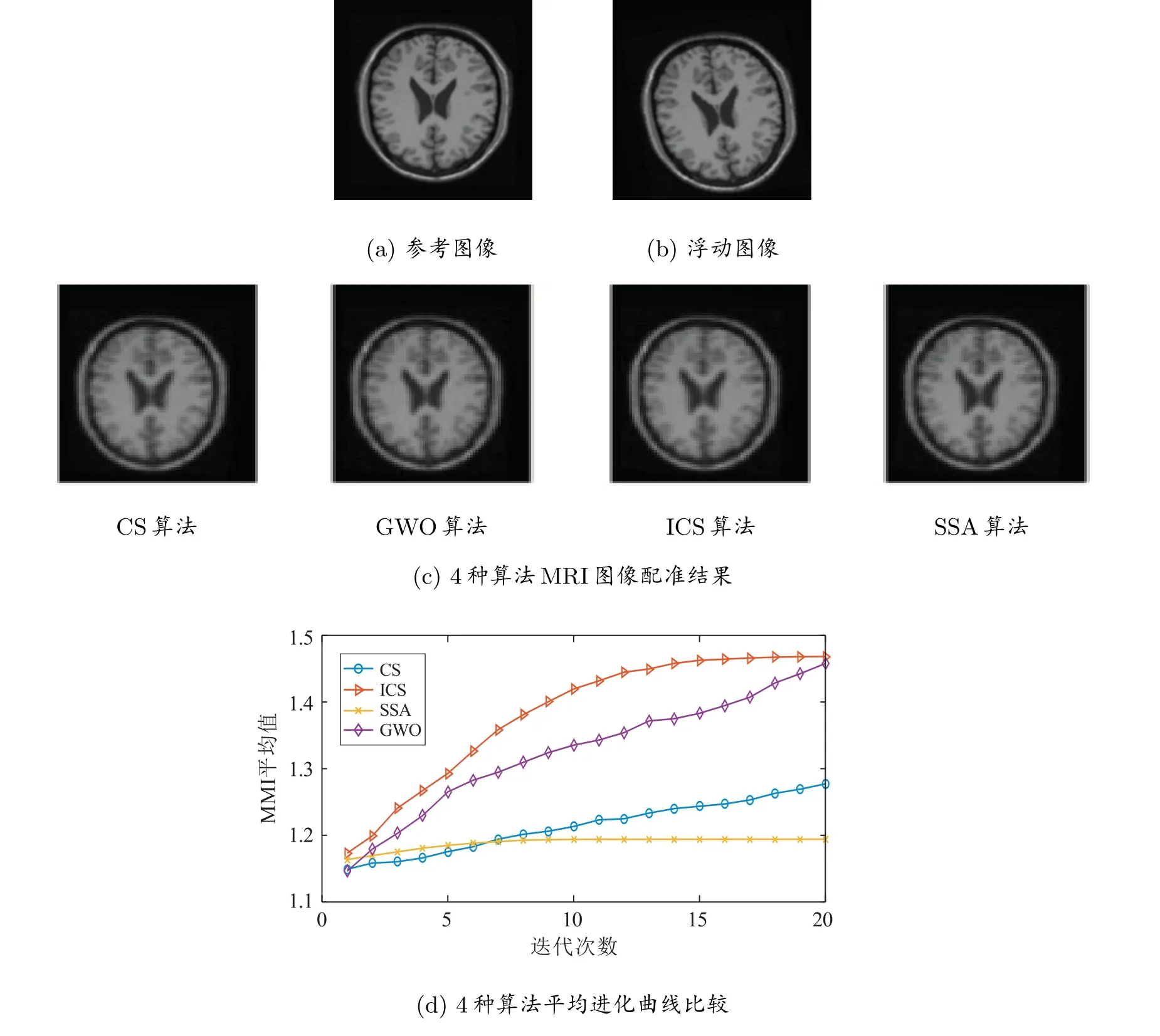
图2 MRI 配准效果

表4 ICS 算法与其他算法的MRI 图比较

实验2 选用脑部图像(256×256)进行配准实验。如图3 所示，图3(a)为参考图像，图3(b)是将参考图像沿水平、垂直方向移动8 个和10 个像素，绕中心旋转20◦得到的浮动图像。同样每个算法独立运行30 次，其它实验参数保持不变。最优配准参数的效果图如图3(c)所示；30 次平均配准参数计算结果如表5 所示；4 种算法平均NMI 值进化曲线比较图如图4(a)所示，4 种算法求解的x、y、θ值折线图如图4(b)∼(d)所示。

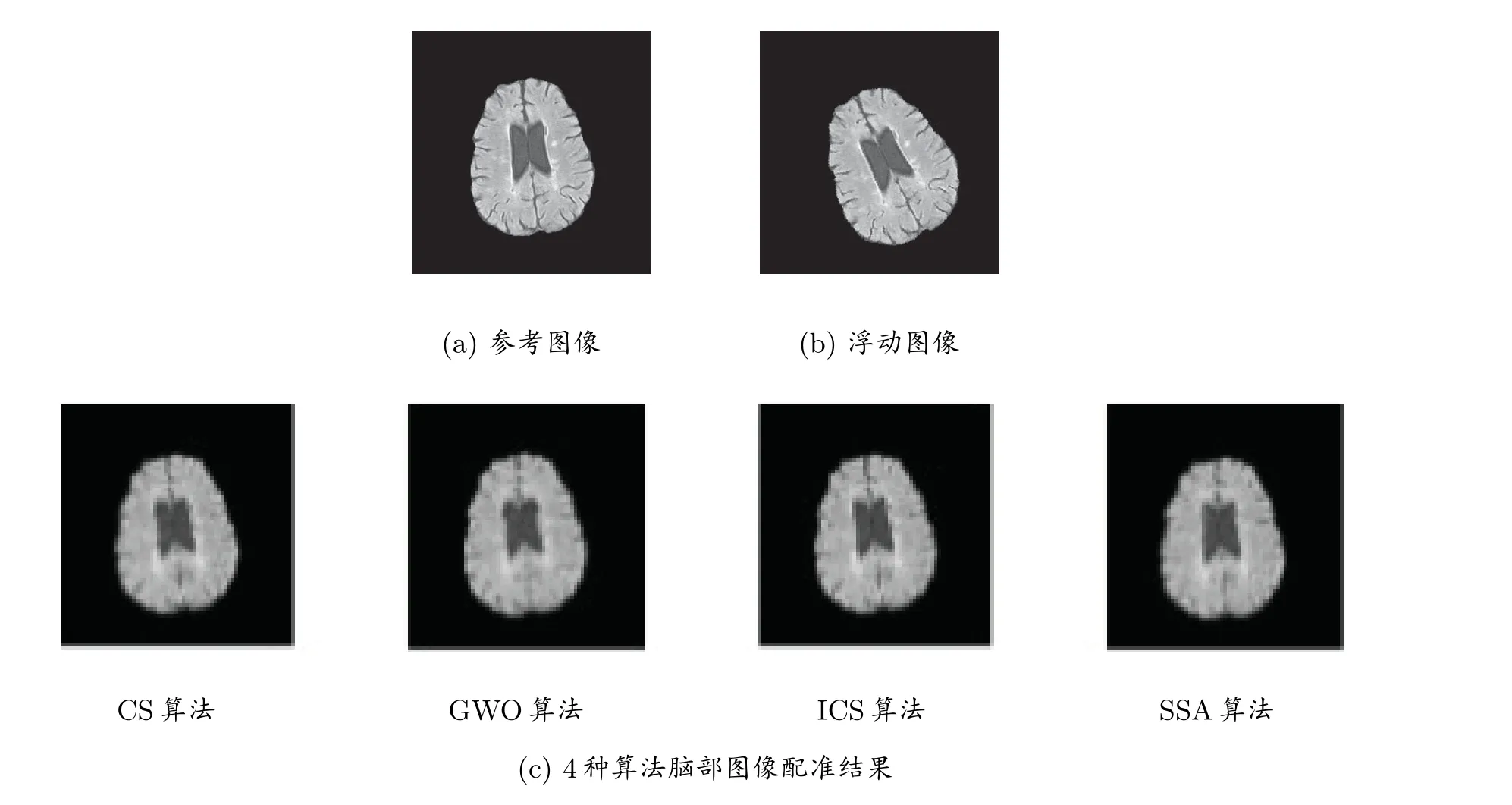
图3 脑部配准效果

图4 4 种算法求解的x、y、θ 的折线图

表5 ICS 算法与其他算法的脑部图比较

从表5 可知：在增大图像尺寸时，ICS 算法的求解性能依然优越，就Delta 值和NMI 值而言，ICS 算法优于其他3 种算法；就运行时间而言，ICS 算法小于CS 算法，但大于GWO 算法和SSA 算法。从图4(a)的4 种算法NMI 值进化曲线比较图可知：ICS 算法依然收敛速度最快、精度更高，且明显优于其他3 种算法。这也进一步说明了改进后的ICS 算法具有更强的全局搜索和局部搜索能力。另外，从图4(b)∼(d)的拆线图可知：GWO 算法、SSA 算法和CS 算法优化的x、y、θ值波动范围较大，大部分结果偏离全局最优解，而ICS 算法优化的x、y、θ值波动范围最小，基本上都在全局最优解x=-8 像素、y=-10 像素和θ=-20◦附近，而且结果较为稳定，这说明改进后的ICS 算法鲁棒性更好。

4 结束语

本文针对基本布谷鸟搜索算法的不足，利用信息分享、局部增强算子和新方式建立鸟巢等来提高种群多样性、局部勘探能力和收敛速度，进而提出了一种新型的布谷鸟搜索算法。通过15 个基准函数和2 个图像配准的仿真实验，所有实验表明，所提算法具有更好的收敛速度、计算精度和鲁棒性。