融合坐标系误差模型的工业机器人运动学标定*

陈 琳,乜聘广,蒙成琦,潘海鸿

(广西大学机械工程学院,南宁 530004)

0 引言

工业机器人由于动作迅速、适应性强等特点已经应用于工业生产的各个领域。由于受绝对定位精度低的影响,工业机器人主要应用于搬运、喷涂、点焊和装配等只对重复定位精度有较高要求的领域[1-2]。为使其可以应用于更加广泛的领域(精密加工、航空航天等),对机器人进行运动学标定来提高其绝对定位精度是非常必要的[3-5]。

机器人运动学标定一般分为运动学建模、误差测量、参数辨识与误差补偿4个步骤[6]。运动学建模是描述机器人运动和进行运动学标定的根本,由于机器人几何参数误差对于机器人绝对定位精度的影响比例达到80%[7-8],因此机器人的运动学建模大部分都是针对于机器人关节连杆几何参数误差建立的[9-10]。

D-H(denavit-hartenberg)参数模型是目前应用最为广泛机器人建模方法,但是D-H模型并不能完整的描述机器人的结构参数。比如当2个平行的旋转轴轴线出现稍许变动,DH 参数就将产生巨大变化,影响建模。为了弥补D-H模型的缺点,一些学者引入了绕y轴旋转量β建立MD-H模型;还有一些学者提出新的运动学模型。OKAMURA等[15]借助旋量理论与李代数提出了指数积模型;ZHUANG等[16]提出了满足“完整性”和 “参数连续性”的CPC模型进行机器人运动学标定;白云飞等[17]基于6参数模型进行误差建模并根据制造公差确定误差参数范围进行机器人运动学参数辨识,但是并未考虑工具坐标系对位置准确度的影响。

为完整的描述机器人的结构误差参数,提高机器人运动学标定后的位置准确度,提出一种融合多坐标系的误差模型实现工业机器人运动学标定。在埃夫特ER6B-C10型6自由度工业机器人上搭建实验平台,验证融合多坐标系误差模型的有效性和准确性。

1 机器人误差模型

1.1 机器人建模

图1为建模得到的机器人坐标系模型。

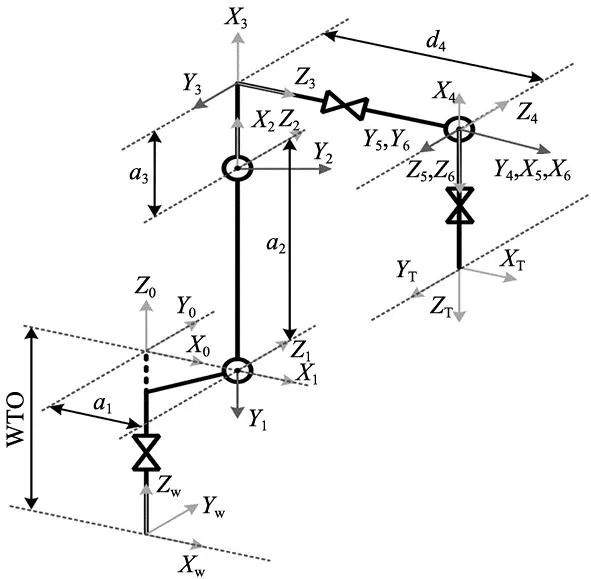
图1 机器人坐标系系统

根据D-H参数模型的描述,相邻杆件坐标系之间的变换矩阵公式为:

(1)

(2)

式中:

n11=cBicCi-sAisBisCin12=-cAisCi
n13=cCisBi+cBisAisCin14=Xi
n21=cBisCi+cCisAisBin22=cAicCi
n23=sBisCi-cBicCisAin24=Yi
n31=-cAisBin32=sAi
n33=cAicBin34=Zi

式(1)与式(2)的参数对应关系:

(3)

1.2 基于6参数模型机器人几何误差模型

由机器人微分运动可知,机器人连杆上某一坐标系微分运动为D=[dTδT]T,其中d=[dxdydz],δ=[δxδyδz],写成矩阵的形式为:

(4)

式中:I3为三阶单位矩阵,[δ]是向量δ的反对称矩阵,d为微分位移量,δ为微分旋转量。

对于机器人同一杆件(视为刚体)的两个坐标系{i-1}、{i},取坐标系{i-1}为参考坐标系,当坐标系{i-1}存在微分误差i-1D时,假设坐标系{i-1}与坐标系{i}之间的齐次变换微分矩阵为dT,则坐标系{i-1}与坐标系{i}之间的变换矩阵T与齐次变换微分矩阵为dT的关系为:

dT=[D-I4]·T=Δ·T

(5)

式中:I4为4阶单位矩阵,Δ为矩阵算子,即一个坐标系的微分变化量可由微分算子乘以该坐标系得到[18]。式中的微分算子Δ是相对于固定坐标系的,故将其记为Δ0,相对于当前坐标系的微分算子即为Δi,根据刚体的微分运动学式(5)可写为:

dT=Δ0·T=T·Δi

(6)

故:

Δi=T-1·Δ0·T

(7)

由6参数模型变换矩阵与相应的运动学公式即可推得6参数模型下的坐标系{i}的微分误差矩阵:

(8)

式中:

m21=-m12=sinAi·δBi+δCi
m13=-m31=-ZisinCiδAi+cosAicosCi·δBi
m23=-m32=cosCi·δAi-cosAi·cosCi·δCi
m14=δXi+Y·δCi-ZisinCi·δAi+
(YisinAi-Zi·cosAicosCi)·δBi
m2,4=δYi+ZicosCi·δAi+(-XisinAi-Zi·cosAisinCi)·δBi
m34=δZi+(Yi·cosAi·sinCi+Xi·cosAi·cosCi)·δBi+
(-YicosCi-XisinCi)·δAi

式中:δXi,δYi,δZi,δAi,δBi,δCi分别是6参数模型中参数Xi,Yi,Zi,Ai,Bi,Ci的误差量。将式中的微分平移量di和微分旋转量δi与6参数模型的几何参数误差量的映射关系写为矩阵形式:

(9)

定义式(9)中的转换矩阵为Hi,且ΔRi,6参数=[δXi,δYi,δZi,δAi,δBi,δCi]T,ei=[dxi,dyi,dzi,δxi,δyi,δzi]T,则式(8)写为:

ei=HiΔRi,6参数

(10)

对于6自由度工业机器人来说,需要将6个关节的误差传递到末端,因此引入关节i到机器人末端法兰的齐次变换矩阵:

(11)

根据微分运动中两坐标系的误差矩阵建立机器人末端位姿的误差模型:

(12)

式中:M1、M2、M3、M4、M5、M6、M7、M8、M9均为3×n矩阵,ΔX=[ΔX1…X6]T,ΔY,ΔZ,ΔA,ΔB,ΔC与ΔX的含义类似。

1.3 工具坐标系误差模型

在对机器人进行几何参数标定时,需要在机器人第6关节处安装靶标(工具点)。由于安装误差,测量过程中会将此误差引入到模型中,导致辨识精度降低。

图2为工具坐标系误差简图,其中{R6}为机器人第6关节坐标系,{TOOL}为工具点坐标系。P点为坐标系{TOOL}在坐标系{R6}的理论位置,P′点为实际位置。忽略工具点的姿态变化,P点与P′点之间的微分误差矩阵为:

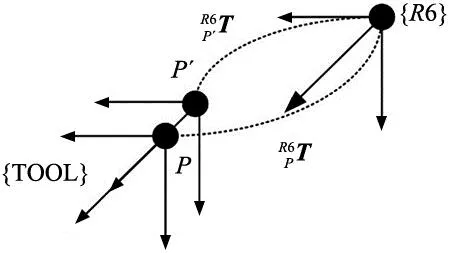
图2 工具坐标系误差简图

(13)

式中:[δXR6,δYR6,δZR6]T为工具坐标系位置误差向量。

因为在串联型6自由度机器人每个杆件的误差是线性叠加的,不考虑机器人姿态的影响,融合多坐标系的误差模型为:

(14)

式中:I3为三阶单位矩阵。

式(14)可简写为:

e总=J·δ

(15)

2 运动学参数辨识方法与补偿方法

运动学参数辨识是将测量的数据代入到误差模型中求解误差参数的过程。由式(15)建立的误差模型可知,为获得机器人几何参数误差必须对机器人末端进行多组采样,将采样数据带入误差模型中构造超定方程,通过线性最小二乘解作为几何参数误差的近似解。

由于机器人扩展雅可比矩阵不是方阵,因此无法直接求解机器人扩展雅可比矩阵的逆矩阵,这里采用矩阵奇异值分解(SVD)的方法分解机器人扩展雅可比矩阵,即:

(16)

式中:V和Q都是正交矩阵,D=diag(σ1,σ2,…,σr),σ1,σ2,…,σr是J的非零奇异值。相应的广义逆矩为:

(17)

因此,将式(17)带入式(15)中可得最小二乘解的表达式:

(18)

运动学补偿是将辨识出的参数误差值补偿到机器人结构参数中。因为对机器人进行全参数补偿会改变机器人逆运动学求解算法,故采用参数降维补偿法。对D-H模型中的参数进行运动学分析发现逆运动学求解算法使用的参数有10个,分别是[θ1～θ6,a1～a3,d4]。由式(3)可得,当θ发生微小变换时,参数a的误差可近似等于参数X的误差。由此参数[θ1～θ6,a1～a3,d4]对应式(14)中的误差参数为[δC1～δC6,δX1～δX3,δZ4],再加上工具坐标系3个误差参数[δXR6,δYR6,δZR6],所以式(14)化简为:

(19)

采用最小二乘法对13个误差参数辨识,将辨识出的参数误差直接补偿到机器人的结构参数和工具坐标系中,完成机器人的误差补偿。如图3所示。

图3 辨识补偿流程图

3 机器人标定与补偿实验

采用美国API型激光跟踪仪测量系统对埃夫特ER6B-C10型6自由度工业机器人进行标定和补偿实验。美国API激光跟踪仪测量系统其测量精度为±10 μm,±3.5 μm/m,此精度远小于未经标定的机器人位置准确度,因此其测量误差在标定过程中可以忽略不记。机器人标定与补偿实验平台如图4所示。机器人DH参数如表1所示。

表1 埃夫特ER6B-C10型6自由度工业机器人D-H参数

图4 机器人标定与补偿实验平台

3.1 机器人几何参数标定与补偿实验

为了减少测量噪声对标定误差的影响,根据埃夫特ER6-C10机器人的实际臂展,在机器人常用的工作空间中选取边长为800 mm的立方体,在立方体中随机均匀的选取50个采样点,分别使用MD-H误差参数模型[19]和融合多坐标系的误差模型进行参数辨识,辨识结果分别如表2和表3所示。

表2 MD-H模型辨识的误差参数

表3 融合多坐标系的误差模型辨识的误差参数

根据辨识结果修正机器人结构参数,并在上述立方体中在选取20个采样点进行位置误差测量。补偿前的误差如图5所示,补偿后误差如图6所示。

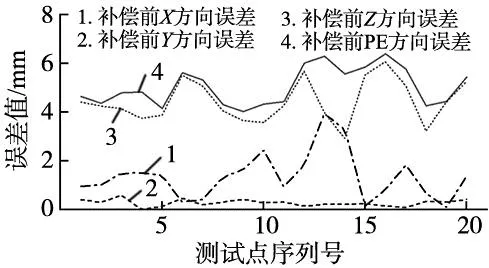
图5 补偿前各测试点各方向误差图

对比标定前的位置误差,经过MD-H辨识补偿后的采样点位置误差均下降到0.8 mm以下,经过融合多坐标系的误差模型辨识补偿后的采样点位置误差均下降到0.3 mm以下,如图6d所示,证明融合多坐标系的误差模型是有效的。

几何参数误差补偿前后各个方向平均误差对比如表4所示。

表4 几何参数误差补偿前后各个方向平均误差对比 (mm)

由表中数据可以看出MD-H法和融合多坐标系均减少了机器人位置误差。MD-H法将平均位置误差由5.047 3 mm下降到0.474 7 mm,精度提高90.59%;融合多坐标系将平均位置误差由5.047 3 mm下降到0.210 7 mm,精度提高95.82%,证明融合多坐标系的误差模型是准确的。

3.2 绝对定位精度检测

根据国家标准《GB/T12642-2013工业机器人性能规范及其试验方法》中对机器人位置准确度检测方法的规定。位置准确度[20]表示指令位置和从同一方向接近该指令位置时的实到平均值之间的偏差。偏差值越小,机器人绝对定位精度越高。首先,在机器人工作空间正前方的一块正方形区域内选取5个测试点,控制机器人按一定顺序循环运动。通过激光跟踪仪测量每个点的实际位置,如此循环30次。几何参数误差补偿前的位置准确度(AP)检验结果,如表5所示。

表5 几何参数误差补偿前的位置准确度 (mm)

完成MD-H误差模型辨识补偿后的位置准确度检验结果,如表6所示。

表6 MD-H误差模型辨识补偿后的位置准确度 (mm)

完成融合多坐标系的误差模型辨识补偿后的位置准确度检验结果,如表7所示。

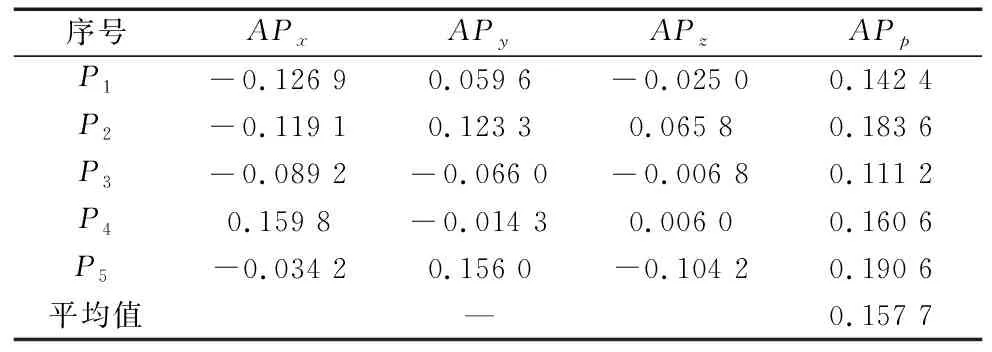
表7 融合多坐标系的误差模型辨识补偿后的位置准确度 (mm)

由表5～表7可知,机器人末端位置准确度经过MD-H误差参数模型辨识补偿后由5.251 0 mm降低到0.306 9 mm,经过融合多坐标系误差模型辨识补偿后由5.251 0 mm降低到0.157 7 mm,两者比较,位置准确度提升了48.61%;由图7可以看出融合多坐标系的误差模型辨识补偿后的位置准确度比MD-H法补偿后的波动较小,说明融合多坐标系的误差模型辨识补偿后的效果更好。

图7 补偿前后各测试点位置准确度对比图

4 结论

针对D-H模型不能完整的描述机器人结构误差的问题,提出使用6参数模型进行机器人坐标系及误差模型的建立。考虑工具坐标系的误差模型,融合到机器人误差模型中,建立融合多坐标系的误差模型。分别使用MD-H法和融合多坐标系的误差模型对埃夫特ER6B-C10型6自由度工业机器人进行标定和补偿实验,并对补偿后的机器人进行位置准确度检测。实验结果表明融合多坐标系的误差模型辨识补偿后的机器人位置准确度相比MD-H误差模型辨识补偿后提高了48.61%,证明了融合多坐标系的误差模型的补偿效果优于MD-H误差模型。