基于动凝聚和线性互补的齿轮动态接触分析*

董昭荣,张 楚,董惠敏

(大连理工大学机械工程学院,大连 116024)

0 引言

齿轮传动在机械领域占有极其重要的地位,齿轮啮合过程中的变形仿真是齿轮设计的关键步骤,然而由于齿轮三维动态啮合有限元接触分析具有高度非线性以及大量的自由度特点,其计算往往不能兼顾精度与效率。

为了提高计算效率,凝聚法是减少计算自由度的有效方法。GUYAN[1]提出静凝聚方法,忽略惯性力的影响;CALLAHAN[2]改进了Guyan缩聚法,计入了部分惯性力的影响;李伟明[3]利用逐级迭代缩减方法验证了迭代级数与计算精度的规律;FRISWELL等[4]迭代改进方法将静凝聚进一步扩展到动力学领域;XIA等[5]重新推导计入质量阵影响的迭代公式,使现有的动凝聚方法收敛速度更快;WEI等[6]直接从简化的振动方程推导出响应灵敏度,提高基于响应的大型结构有限元模型修正的计算精度和效率。

齿轮的接触分析对研究其传动性能有重要意义。VIDEKEY[7]提出应用赫兹接触理论得到齿轮应力于啮合线方向的变化规律;LITVIN等[8]利用微分几何和解析法研究了齿轮啮合的接触条件;谭自然[9]基于解析法研究齿根裂纹对齿轮时变啮合刚度及动态接触特性的的影响。ZHANG等[10]基于点面线性互补方法提出解决三维齿轮准静态接触分析方法。

目前,现有的动凝聚方法多数基于静凝聚公式基础上对其计入惯性力的影响,针对不同的计入方式出现许多动凝聚的改进方法,其中迭代改进方法最为常见。物理型缩减技术方面,三级近似递推缩减公式的精度最好[3],但是目前还未有人基于三级近似递推缩减公式推导其迭代改进的动凝聚公式。据此针对大型结构的有限元模型,本文推导了一种新的动凝聚公式,并且应用到齿轮的动力学接触分析研究中。有限元方法是研究齿轮的动力学接触分析的主要方法,但是其非线性运算使其分析过程需要占据大量的资源,针对这一问题,本文在有限元方法的基础上,结合动凝聚方法、Bozzak-Newmark方法以及文献[11]中点面线性互补方法,推导出新的齿轮动态接触分析求解方程。并且利用本文研究方法计算了一对斜齿轮的接触应力,与ANSYS斜齿轮对的动态接触分析结果进行对比,该方法计算效率与计算精度得到了验证。

1 新的动凝聚方法分析

动凝聚方法可以减少运动微分方程计算自由度,极大的提高结构动力分析的效率。对于具有N自由度模型的运动微分方程:

(1)

式中:[M]是质量阵,[C]是阻尼阵,[K]是刚度阵,{Q(t)}为位移向量,{F}为系统所受外力向量。为减少计算量,构造缩减矩阵[T],将整体自由度凝聚到主自由度上,即:

{Q(t)}=[T]{q(t)}

(2)

将式(2)代入式(1),并在式(1)两边同时乘以缩减矩阵的转置可得:

(3)

式中:[MR]=[T]T[M][T]、[CR]=[T]T[C][T]、[KR]=[T]T[K][T]、{FR}=[T]T{F}分别为凝聚后的质量阵、阻尼阵、刚度阵和外部力向量。凝聚方法的差别之处主要在于缩聚转换矩阵[T]不同[1]。WEI等[6]针对大型结构从简化的振动方程推导一种动凝聚方法提高了有限元模型的计算精度与计算效率。其最终缩减矩阵由以下公式计算:

(4)

(5)

为验证其与传统动凝聚关系,将上述公式[M]d反代入到迭代方程(4)得:

(6)

由此可见,文献[6]中利用二级近似递推缩减公式迭代计算缩减矩阵,根据张德文推导缩减公式,三级近似递推缩减公式计算精度最高,因此重新推导分块后n自由度系统的运动微分方程:

(7)

根据上式的第二行可得:

(8)

(9)

(10)

(11)

(12)

(13)

(14)

三级近似模型缩聚公式精度高于二级近似模型缩聚[3],因此利用基于文献[6]二级近似模型缩聚迭代改进思想,利用迭代思想重新计入三级近似模型缩聚公式中的惯性力的影响,进一步提高动凝聚的计算精度。

动态凝聚方法是处理大型有限元结构问题的有效方法。利用转换矩阵[T],将整体计算自由度转换为主自由度,从而使用变换矩阵形成更小计算自由度的简化系统。在凝聚之前的计算自由度达到108,凝聚之后的自由度仅仅为104。因此,对简化系统进行接触分析可节省大量计算时间。

2 斜齿轮系统的动力学点面线性互补接触分析

根据文献[10]对于一对斜齿轮有限元模型,为建立主从动齿轮之间的点面互补模型,假设主动齿轮2为接触体,从动齿轮1为目标体。接触体上潜在接触区域的点分别对应于目标体上潜在接触区域面网格中的最小的面,如图1所示。主从动齿轮之间的法向接触力{Fn}与接触间隙{gn}形成互补关系,即为:

图1 主从动齿轮接触单元(ok-pk为接触面法线方向)

{Fn}·{gn}=0,{Fn}≥0,{gn}≥0

(15)

因此,本文第2节的内容围绕如何对上式建立惩罚方程进行展开。首先在目标体建立全局坐标系S{O:x,y,z},在接触体上潜在接触区域内每一个节点为原点建立节点坐标系Sk{ok;nk,αk,τk},k是接触体上第k个节点ok。

本文假设边界条件为初始速度、加速度和位移均为0。

斜齿轮的重合度一般为2～3,在啮合过程中,最多有3个齿面同时接触。因此分别选择有限元模型上主动轮3个接触齿面节点和中心,以及从动齿轮的3个接触齿面的节点作为主自由度所在节点,如图2和图3所示,并且在ANSYS验证时将3对接触面设置接触对。将凝聚后的坐标代入两个齿轮的运动微分方程,方程两侧同乘[T]T可得:

图2 灰色圆点表示从动齿轮1主自由度所在节点 图3 灰色圆点表示主动齿轮2主自由度所在节点

(16)

式中:[MR]=[T]T[M][T],[CR]=[T]T[C][T],[KR]=[T]T[K][T],{FR}=[T]T{F}。

由文献[10]可知变形后间隙与初始间隙与目标体位移与接触体位移关系为:

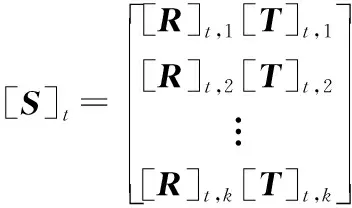
(17)

式中:{gn}为变形后接触体节点与目标面间隙,{gn,0}为初始间隙,{q}t为目标体节点位移向量,[S]t将目标体上节点沿全局坐标系下的位移变换为接触体节点映射在目标面上节点沿法向接触方向的位移,{qn}c为接触体节点沿法向接触力方向位移。

根据换齿的过程,在整个齿轮啮合的过程中,可视为换齿过程的循环,因此可以只研究一个换齿时间段的应力变化,将时间等距离散。

根据Bozzak-Newmark方法[11],令αB=0.2,βB=0.5,γB=0.25,接触体凝聚后运动微分方程可以转换为:

[K*]c{q}c,j+1={QR}c-{QRF}c,j+1+{F*}c,j+1

(18)

根据文献[10]消去接触体平衡方程中切向力影响,经推导后接触体沿法向接触方向的平衡方程为:

(19)

同理,凝聚后的目标体平衡方程经Bozzak-Newmark方法转化后,利用虚功原理可得到目标体沿法向接触方向的平衡方程[10]可以表示为:

(20)

将最终推导的接触体和目标体的运动微分方程代入到文献[10]中推导所得几何方程(17)消除节点位移,得到接触间隙和力的关系式:

(21)

最后整理出接触体和目标体线性互补求解方程为:

(22)

式中:

根据接触体平衡方程,目标体平衡方程,间隙位移关系,消去接触体和目标体的节点位移得到最终的线性互补方程。此时结合lemke算法可以得到各个时刻的接触压力和接触间隙,并反带入到主从动齿轮的运动微分方程,得到各时刻齿轮的变形位移。

3 验证示例

为验证推导得到动凝聚方法的有效性,利用ANSYS中beam188单元建立轴-圆盘有限元模型,如图4所示,内孔直径0.02 m,外径从左到右依次为0.03 m、0.04 m、0.02 m、0.03 m,长度从左到右依次为0.4 m、0.6 m、0.6 m、0.4 m,弹性模量2.01 GPa,泊松比0.3,密度7.8e-3 kg/m3,圆盘质量0.35 kg,圆盘直径0.04 m,设置在轴中心节点处。

图4 轴-圆盘有限元模型

图5 各方法计算中心节点位移结果对比图

图6 计算步骤示意图

对轴中心节点处施加绕X轴转矩M=10*sin(t),分别利用完全法、新凝聚方法计算得到中心节点位移变化。

利用该凝聚方法计算中心节点Y方向平稳后一个变化周期内最大位移为3.583×10-5,Wei Tian所提出凝聚法的计算误差0.885%,完全法计算得到3.615×10-5,计算误差为0.58%,计算时间由完全法的9.23′′缩短为1.201′′,计算精度约为Wei Tian法的1.53倍,由此验证了所推导得到的新凝聚公式的有效性。

为验证动态线性互补接触分析方法的有效性,以本文研究方法和ANSYS瞬态动力学完全法对斜齿轮对在固定转矩和固定转速条件下进行接触分析。

两个齿轮的法向模数为m=3.0,齿数为36,压力角20°,齿宽0.03 m,螺旋角15°/-15°,弹性模量2.06 GPa,泊松比0.3,密度7.85e3 kg/m3,材料阻尼0.004 N·s/m。对主动齿轮中心施加100 rad/s的转速,对从动轮施加100 N·m的边界条件,为防止产生较大冲击,采用斜坡函数形式加载转速和转矩。设置收敛条件为:

|ωk-ωk-1|/ωk≤ε

(23)

式中:k为迭代次数,ω为固有频率,设误差容差ε为10-4。以下是利用ANSYS和本研究方法计算的在各时刻主动齿轮最大接触压力和传动误差随时间变化图形。

根据图7和图8可知,ANSYSY瞬态动力学与所提出的线性互补接触分析方法结算结果中,最大接触压力相对误差为4.01%,最大传动误差差值相差0.94%,将图2和图3中的主自由度对应的接触对分别设置为1、2、3。两种齿轮动态接触分析方法在0.006 s和0.007 2 s齿面接触压力分布图对比情况为如图9和图10所示。

图7 最大接触压力时域图 图8 传动误差时域图

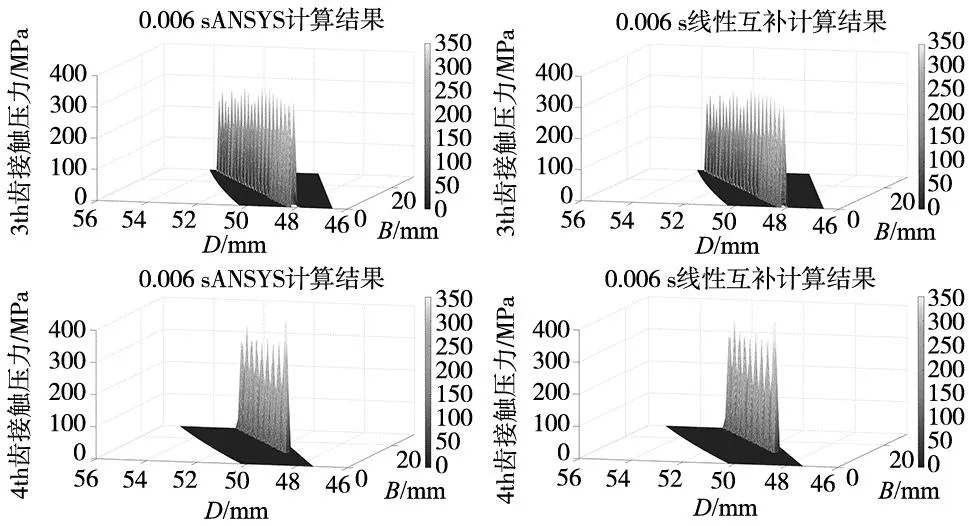
图9 0.006 s各齿面接触压力分布情况对比

图10 0.007 2 s各齿面接触压力分布情况对比

0.006 s时刻ANSYS计算最大压力为473.1 MPa,线性互补方法计算值为455.5 MPa,相对误差为3.72%;0.007 2 s时刻ANSYS计算最大压力为536.3 MPa,线性互补方法计算值为550.7 MPa,相对误差为2.69%。

利用缩减转换矩阵将运动微分方程中的全阶自由度凝聚到更少的主自由度上,在凝聚前自由度大约为109,凝聚后的自由度约为104,极大的减少计算量,利用ANSYS瞬态动力学分析计算需要总时间为3060′58′′,而利用线性互补方法求解需要总时间为395′59′′。因此该方法具有较好的精度与较高的计算效率。

4 结论

针对大型结构有限元模型,本文利用迭代方法,对三级近似迭代动凝聚公式重新计入惯性力的影响,提高动凝聚公式计算精度。利用动凝聚方法可将计算自由度缩减到所选主自由度上,减少分析过程计算量,然后结合点-面线性互补方法完成了齿轮的动态接触分析。由算例可知该方法在一定的转速和扭矩下具有较高的计算精度和计算效率。本文为动凝聚方法以及齿轮动态有限元接触分析提供了新的有效的思路。