基于改进ESO和分数阶滑模的PMSM转速控制*
任金霞,何明晏,姚广辉
(江西理工大学电气工程与自动化学院,赣州 341000)
0 引言
永磁同步电机不仅构造简单,效率也比普通感应电机高,已经在工农业生产、船舶等领域当中广泛应用[1]。当电机控制系统受到内外部扰动时,传统滑模控制系统的稳定性和抗干扰能力并不能达到实际的控制条件[2]。因此,需要设计改进分数阶滑模控制器来代替传统滑模控制器,使得电机转速控制达到期待的控制效果[3]。另外,机械传感器会影响电机控制系统的稳定性,给实际的系统控制带来很大的局限性。而无传感器控制技术可以避免机械传感器带来的众多弊端[4]。而扩展状态观测器(ESO)是无传感器控制技术中最好的技术之一。ESO不仅可以用来观测电机的转速信息,还能精确估计电机控制系统受到的内外部扰动[5]。
侯孝涵等[6]将滑模控制与反馈线性化理论相联系,并提出了一种新型双幂次趋近律,设计出具有抗干扰能力强、动态性能好等优点的新型电机控制系统。郑美茹等[7]将分数阶次符号函数与滑模控制相结合,提出了新型的滑模控制策略,仿真结果证明了该策略具有上升时间短、鲁棒性好等优点。郭小定等[8]提出了一种新型指数趋近律,并设计了一种新型的永磁同步电机滑模控制系统,实验结果证明该方法能够提高系统的瞬态性能指标和稳定性。彭秋铭等[9]设计了一种新型ESO,并设计了转子观测器,仿真结果说明该方法能够精确估计转子的位置和速度,具有良好的抗干扰性能。
为了解决传统滑模控制系统中的动态、稳态性能和抗干扰性能不佳的问题,本文将分数阶控制理论引入到滑模变结构控制中。本文提出了一种新型分数阶趋近律,设计了一种改进的非线性比例积分滑模面,并由此实现了一种改进分数阶滑模转速控制器的设计。同时,利用改进的非线性转速环ESO来估算电机系统的内外部扰动,提高电机转子速度的观测精确度和系统的抗干扰能力。
1 分数阶微积分理论
分数阶微积分理论在工程应用领域有大的发展前景,其衍生的分数阶控制也是控制领域中的热门方向。其中,分数阶控制中的操作算子可以定义为:
(1)

分数阶导数有多种定义,而R-L分数阶微积分运用最为广泛,其定义为:
(2)
式中:n-1<β≤n,Γ(·)为欧拉的Gamma函数。
2 永磁同步电机数学模型
将表贴式三相PMSM作为控制对象,并选用id=0控制的控制方法,其在d-q坐标系下的数学模型为:
(3)
式中:R为定子电阻,ud、id为d轴的定子电压和电流,uq、iq为q轴的定子电压和电流,ψf为磁链,L为定子电感,J为转动惯量,pn为极对数,ωm为机械角速度,TL为负载转矩,B为阻尼系数。
3 PMSM转速控制系统设计
为了解决传统滑模控制系统中的动态、稳态性能和抗干扰性能不佳的问题,本文采用改进的分数阶滑模转速控制器(FOSMC)代替传统滑模转速控制器,采用改进的非线性转速环扩展状态观测器(ESO)来获取精确的转子速度信息和系统的内外部扰动误差。PMSM控制系统的控制策略总框图如图1所示。
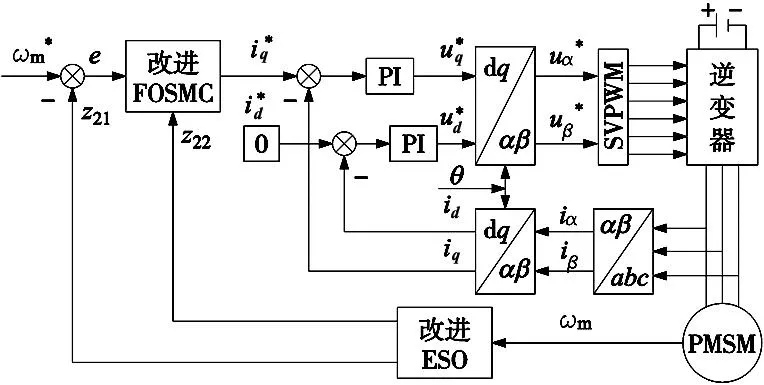
图1 PMSM控制策略总框图
3.1 转速环扩展状态观测器(ESO)的设计
在三相PMSM控制系统中,多个控制变量之间存在耦合程度大、非线性程度高的情况。当控制系统受到内外部扰动的影响时,传统的滑模控制方案存在稳定性差的局限性。扰动ESO不仅可以精确估计系统的内外部扰动大小,还具有精准观测电机转速的能力。
当考虑电机自身参数变化和外部扰动时,永磁同步电机的运动方程为:
(4)

选取参数λ和μ分别表示内部和外部扰动,其表达式为:
(5)
故式(5)可简写为:
(6)
根据式(6),定义x1=ωm,x2=μ,则式(6)可改写为:
(7)
式中:ϑ为x2的扰动。
基于双曲正切函数的常规非线性ESO的表达式为:
(8)
将改进指数型函数Φ1(eγ,τ1)代替式(8)中的双曲正切函数,来削弱系统的抖振情况,Φ1(eγ,τ1)的表达式为:
(9)
式中:τ1>0用来表示边界层厚度。
则改进的非线性转速环ESO的表达式为:
(10)
3.2 分数阶滑模控制器的设计
定义给定的电机转速参考值为ωref,则PMSM控制系统的转速误差可表示为:
e=ωref-ωm
(11)
对式(11)进行求导运算,并结合式(6),则得:
(12)
结合PMSM系统的状态控制变量,将传统积分滑模面设计为:

(13)
式中:c为积分滑模面参数,c>0。
本文将非线性函数Φ2(e,τ2)代替式(13)中的转速误差函数e(ξ)。非线性函数Φ2(e,τ2)可以放大转速误差,使系统在较小的误差情况下,也能拥有优异的控制性能。Φ2(e,τ2)的表达式为:
(14)
式中:τ2为边界层厚度,τ2>0。
在传统积分滑模面的基础上,设计改进的非线性比例积分滑模面为:

(15)
式中:kp>0,ki>0。
将反正弦三角函数作为开关函数,来削弱系统的抖振现象,Φ1(s)的表达式为:
(16)
式中:τ3>0用来表示边界层厚度。
另外,定义一个sigmoid型函数为:
(17)
式中:a为正常数。
通过研究分数阶微积分理论,并结合常用的指数趋近律函数,设计了新型分数阶趋近律,其表达式为:
(18)
式中:x为系统状态变量,ε>0,k>0,0<α<1,0<β<1,0 (19) (20) 对式(20)进行导数运算,并结合式(12)、式(15)和式(18),得: (21) 在MATLAB/Simulink环境下进行仿真实验来验证改进的PMSM控制系统的可靠性,控制方式采用id=0控制。 在图2中给出了PMSM控制系统的控制策略对比框图。 图2 PMSM控制策略对比框图 表1给出了表贴式PMSM控制系统的仿真参数。 表1 PMSM控制系统仿真参数 在式(18)定义的新型分数阶趋近律和式(13)定义的传统积分滑模面的基础上,设计了新型分数阶滑模控制器(FOSMC)。并与由式(8)定义的常规非线性ESO相结合,实现了PMSM新型分数阶滑模控制系统的设计。 本文将式(15)代替式(13),提出了改进的非线性比例积分滑模面,并与式(18)定义的新型分数阶趋近律相结合,实现了改进的分数阶滑模控制器的设计。同时,将式(10)代替式(8),设计了改进的非线性转速环ESO。在改进的分数阶滑模控制器和非线性转速环ESO的基础上,实现了改进的PMSM分数阶滑模控制系统的设计。 对于PMSM的转速环滑模控制,分别对传统滑模控制、新型分数阶滑模控制和改进的分数阶滑模控制的情形进行系统仿真,并在不同实验条件下验证这3种控制策略的抗干扰性和动态性能。统一的仿真初始条件为:仿真时间设为0.4 s,给定电机转速设为800 r/min。 电机空载启动,系统仿真曲线及数据结果,如图3和表2所示。 表2 空载状态下的系统仿真数据 (a) 电机转速 (b) 电机转速估计误差 由图3和表2可知,当系统空载启动时,在改进的分数阶滑模控制策略下,控制系统的峰值时间比传统滑模控制和新型分数阶滑模控制情形下都更短,并且超调量也更小,则说明改进的分数阶滑模控制系统具有更好的动态性能。另外,改进的分数阶滑模控制系统的稳态误差仅为0.025转,几乎可以忽略不计,则说明其具有更好的稳态性能。 电机空载下启动,电机转速在0.2 s时由800 r/min突加至1200 r/min。系统仿真曲线及数据结果,如图4、表3和表4所示。 表3 突加转速时的系统仿真数据 表4 突减转速时的系统仿真数据 (a) 电机转速 (b) 电机转速估计误差 由图4、表3和表4可知,当系统突加突减转速时,在改进的分数阶滑模控制情形下,与其他两种控制情形下相比,其峰值时间、调节时间都更少,具有更好的过渡过程响应指标。同时,在突加突减转速两种情况下,改进的分数阶滑模控制系统的转速波动和稳态误差都更小,拥有更强的抗干扰能力。 电机空载下启动,系统在0.2 s时突加5 N·m转矩负载,在0.35 s时突减转矩负载至3 N·m。系统仿真曲线及数据结果,如图5、表5和表6所示。 表5 突加负载时的系统仿真数据 表6 突减负载时的系统仿真数据 (a) 电机转速 (b) 电机转速估计误差 由图5、表5和表6可知,当系统突加突减负载时,与传统滑模控制和新型分数阶滑模控制情形下进行比较,改进的分数阶滑模控制系统具有更短的调节时间,具有更好的系统稳定性。另外,在突加突减负载两种情形下,改进的分数阶滑模控制系统的转速波动和稳态误差都更小,拥有更强的削弱抖振能力。 由于PMSM控制系统的数学建模可能存在偏差,故改变电机内部参数,分析PMSM控制系统在传统滑模、新型分数阶滑模和改进分数阶滑模控制下的响应情况。系统电机空载下启动,将系统仿真参数中的转动惯量J由0.000 2 kg·m2倍增0.000 4 kg·m2,其他参数仿真参数保持不变。系统仿真曲线及数据结果,如图6、表7所示。 表7 改变转惯量时的系统仿真数据 (a) 电机转速 (b) 电机转速估计误差 由图6、表7可知,当系统改变转动惯量时,与传统滑模控制和新型分数阶滑模控制情形下相比,改进的分数阶滑模控制系统具有更短的峰值时间,具有更好的阻尼程度。同时,改进的分数阶滑模控制系统的稳态误差仅为0.03转,分别是传统滑模和新型分数阶滑模控制情形下的7.5%和16.7%, 则说明其具有更好的鲁棒性。 本文提出了一种改进的非线性比例积分滑模面,以及一种新型分数阶趋近律,并由此设计出改进的分数阶滑模转速控制器。同时,设计了改进的非线性转速环ESO来代替常规的转速环ESO,实现了系统扰动和转速的精确估计。最后在MATLAB/Simulink环境下进行实验仿真,对传统滑模、新型分数阶滑模和改进分数阶滑模3种控制情形下的仿真结果进行比较,并判断3种控制策略下系统控制性能的优劣。结果表明,本文设计的改进的PMSM分数阶滑模控制系统,可以明显改善系统抖振情况,系统稳定性和抗干扰能力明显增强,还可以提升系统的动、稳态性能。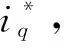

4 稳定性分析
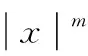
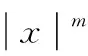


5 仿真结果及分析


5.1 空载状态下的系统仿真

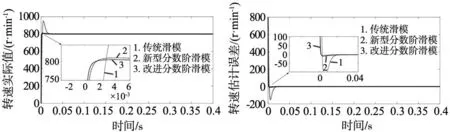
5.2 突加突减转速时的系统仿真
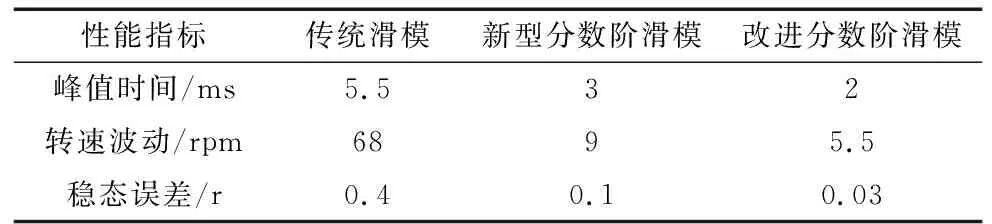


5.3 突加突减负载时的系统仿真
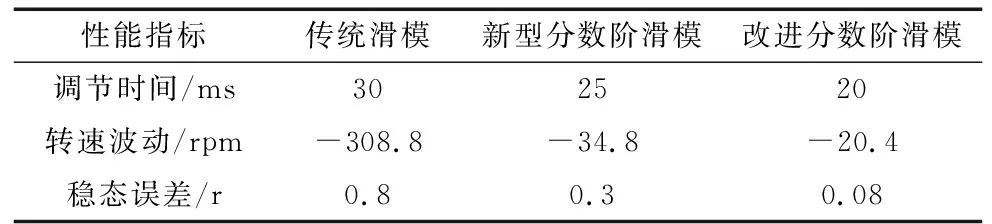


5.4 改变转动惯量时的系统仿真

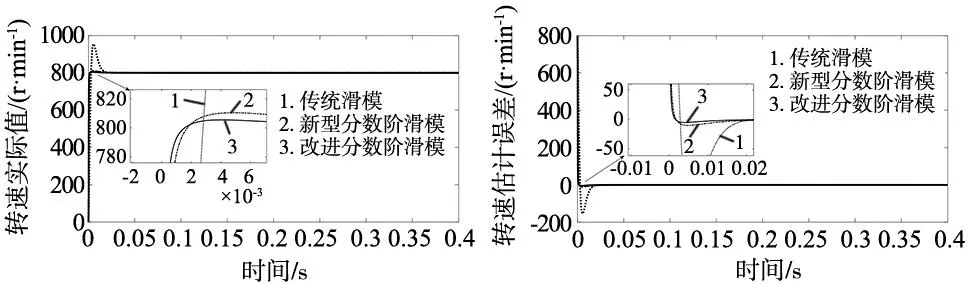
6 结论

