改进扰动观测器的IM自适应滑模反步控制*
满忠璐,于海生,孟祥祥,杨 庆,王建坤,崔 鹏
(青岛大学 a.自动化学院;b.山东省工业控制技术重点实验室,青岛 266071)
0 引言
异步电机,又称感应电机(induction motor,IM)。目前,学者们设计了不同的控制算法,来提高非线性系统的控制性能,如反步控制、滑模控制和自适应控制等。在这些控制方法中,滑模控制具有良好的鲁棒性并且对系统参数精度要求不高[1-2]。然而,传统的滑模控制会产生抖振,这就使得系统的控制精度下降。因此,如何抑制抖振成为滑模控制研究的关键[3-4]。
解决滑模抖振的方法有很多种,例如,高阶滑模、改进趋近律等。GUO等[5]设计一种自适应高阶滑模的方法来减小抖振并增强了系统的鲁棒性;宁博文等[6]应用二阶Super-Twisting滑模控制方法有效的削弱了抖振对系统的影响;ZHOU等[7]借由全阶终端滑模来消除奇异性并减小抖振;ZHANG等[8]设计了一种改进的恒速率趋近律,用以平衡提高系统响应速度的要求与减小抖振的要求。JUNEJO等[9]利用自适应滑模趋近律来提高跟踪精度、减小抖振;WANG等[10]将系统状态变量的功率项和开关增益项纳入传统的指数趋近律中,可以有效地抑制滑模抖振,提高系统状态到达滑模表面的收敛速度。
一般来说,趋近律方法是系统状态对应的控制增益函数,用来满足鲁棒性和减少抖振。在趋近的过程,将控制增益调整到一个较大的值,使系统轨迹快速到达滑模面。在滑动阶段,控制增益降低到一个小值,以减少控制信号中的抖振。因此,在存在扰动和不确定性时,滑模面附近的鲁棒性降低[11-12]。
本文针对滑模抖振的问题,提出了一种基于自适应趋近律的滑模控制方法,根据系统状态与滑模面的变化来减少抖振和趋近过程时间。设计改进的干扰观测器来消除干扰的影响。本文在以上文献的基础上,进一步缓解了快速性与抖振之间的冲突,并消除了超调。实验结果表明,所设计控制方法解决了控制系统内部参数不确定、外部负载未知和摩擦等问题,实现了良好的速度跟踪性能。
1 异步电机的数学模型
在d-q同步旋转坐标系下异步电机数学模型[13]:
(1)
式中:λs=[λsdλsq]T、λr=[λrdλrq]T为d、q轴定转子磁链,is=[isdisq]T、ir=[irdirq]T为d、q轴定转子电流,us=[usdusq]T为d、q轴定子电压。
对式(1)第一行变换得:
(2)

结合式(1)、式(2),按转子磁场定向简化电机模型并写成状态方程的形式:
(3)
式中:
2 自适应滑模反步控制器设计
图1为异步电机自适应滑模反步控制的系统框图,自适应滑模反步控制器调节系统的动稳态性能,扰动观测器输出扰动补偿,消除集总扰动影响。

图1 改进扰动观测器的异步电机自适应滑模反步控制框图
定义x4和x3的跟踪误差为:
(4)
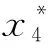
(5)
取
(6)

(7)
选择系统滑模面为:
s=cφ1+φ2
(8)
式中:c为滑模面系数。
求取滑模面的时间导数:
(9)
一般趋近律如式(10)所示。
(10)
上述趋近律,通过设计较大值的ε、k可以使控制器具有较好的响应速度,然而由于滑模控制器的固有特性,较大值的ε、k会使系统的抖振增大。
为了进一步抑制抖振现象,选用sat(s)函数来替代sgn(s)函数并将饱和函数定义为:
(11)
以上饱和函数的含义可以表示为:在▽所界定的范围内,是线性反馈控制;在▽所界定的范围之外,是开关控制。
因此同时考虑系统的动态及稳态性能设计如下趋近律[12]:
(12)

结合式(9)和式(12)得到:
(13)
选择李雅普诺夫函数为:
(14)
对式(14)求导可得:
(15)
为使系统稳定,令:
(16)
此时kλ>0,式(15)可表示为:
(17)
由式(5)可得:
(18)
定义电流误差为:
(19)
对式(19)求导可得:
(20)

选择李雅普诺夫函数:
(21)
对式(21)求导可得:
(22)
为使控制器渐近稳定,令:
(23)
此时,可以得到控制律为:
(24)
将式(23)代入式(22)可得:
(25)
控制器渐近稳定。
3 观测器设计
3.1 扰动观测器设计
根据电磁转矩方程与运动方程可得:
(26)
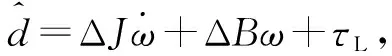
(27)
由式(26)和式(27)可得:
(28)
为了解决扰动对电机系统控制的影响,采用扰动观测器来消除扰动对系统的影响,扰动观测器为[14]:
(29)


(30)
式中:I0>0为电流的上限,根据式(27)可得:
(31)
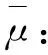
(32)


(33)
根据式(28)和式(32)设计扰动观测器,为:
(34)
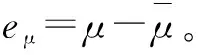
为了证明该扰动观测器的稳定性,定义Lyapunov函数Vdo。
(35)

(36)
3.2 磁链观测器选择
本文所用磁链观测器为文献[16]所设计的滑模磁链观测器,磁链观测器为:
(37)
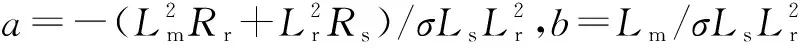
(38)
由文献[16]所知所设计观测器为渐近收敛的。
(39)
3.3 稳定性分析
定义整个系统Lyapunov函数为:
V=V2+Vfo+Vdo>0
(40)
对式(40)求导得:
(41)
由Lyapunov稳定性判据和Lasalle不变集可知,整个控制系统是渐近稳定的。
4 仿真实验验证
在MATLAB/Simulink环境中搭建异步电机控制系统。其中包括异步电机模型、SVPWM逆变器、坐标变换、磁链观测器、扰动观测器和自适应滑模反步控制器等模块,电机参数如表1所示。所示控制器的参数在合适的范围内由试凑法得出,参数较大时系统响应速度变快,稳定性较差;参数较小时,响应速度变慢,为了使系统动稳态性能均表现良好,选定控制器参数为:kλ=150,kid=kiq=1500,k=12,ε=0.7,η=7。观测器的参数同样在合适的范围内由试凑法得出,k1过大会导致波形失真,其余参数变化与控制器相似,磁链观测器参数为:k1=0.001,k2=k3=k4=100,p=q=0.5。扰动观测器参数L=1500,kω=15。
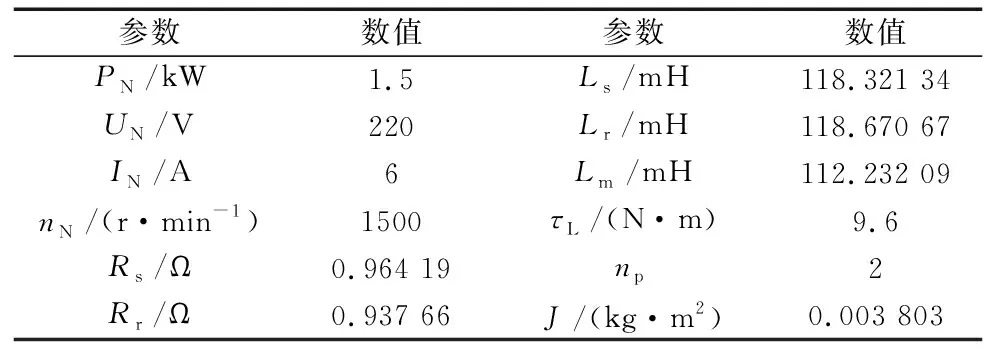
表1 异步电机参数
4.1 无负载转矩注入时的仿真结果与分析
为了说明与传统的SMBC相比,该ASMBC能够有效的减小抖振并缩短到达时间,在不考虑系统的干扰的情况下进行本实验。图2为当给定速度从200 r/min变为700 r/min时,电机的速度响应。如图2所示,ASMBC的到达时间0.043 s,比SMC方法的到达时间0.075 s要快。此外,如图3所示ASMBC的isq抖振明显小于SMBC。

(a) ASMBC转速曲线 (b) SMBC转速曲线图2 转速曲线
图4和5为在速度变化时,DO和IDO与ASMBC结合的实验结果。可以看出,所提出的IDO可以有效地避免在速度突然改变时出现的超调问题。如上一节所述,DO中的积分项μ导致了对扰动的错误估计,而IDO解决了该问题。

(a) ASMBC+IDO转速曲线 (b) ASMBC+DO转速曲线图4 转速曲线
4.2 负载突变时的仿真结果与分析
图6为突加负载转矩时,ASMBC+IDO和SMBC的速度变化变化。在1 s时增加2 N/m的负载转矩,在2 s时取消,如图所示ASMBC+DO的控制方法在负载突变时,最大约有150 r/min的转速波动;而ASMBC+IDO的转速波动最大只有约24 r/min,且调节时间要短得多。因此ASMBC+IDO控制方法比SMBC控制方法的抗干扰能力更好。

(a) SMBC转速曲线 (b) ASMBC+IDO转速曲线图6 转速曲线
5 结论
本文设计了自适应滑模反步的控制策略并改进了扰动观测器。利用反曲正弦函数设计自适应律改进滑模趋近律,加了快电机系统的动态响应速度并抑制滑模控制中的抖振现象。然后,为了消除传统扰动观测器中由于积分项累积带来的超调现象,采用饱和函数改进了扰动观测器,用以估计电机内部参数的变化和外部扰动并减小超调。仿真结果表明,扰动观测器可以快速估计扰动值并且不会给控制系统带来超调。本文的控制策略使异步电机控制系统的响应速度增强、抖振减小,并有效的抑制了负载扰动,使控制系统具有良好的动态性能、稳态性能和鲁棒性。最后,实验结果验证了该控制方法的有效性。

