基于科氏质量流量计的微米级煤尘和岩尘颗粒分类方法

刘丹丹,朱鸿飞,李德文,郭胜均,汪春梅

(1. 黑龙江科技大学 电气与控制工程学院,黑龙江 哈尔滨 150022; 2. 中煤科工集团重庆研究院有限公司,四川 重庆 400037)

煤炭在我国能源中的主体地位在短期内无法动摇,煤炭行业必须走出一条低碳化、高效、清洁的道路,助力实现“碳中和、碳达峰”愿景[1-3]。在煤矿开采过程中,产生的矿尘主要为煤尘和岩尘,二者危害性极大,而且岩尘颗粒的粒径要比煤尘的小得多,更易被人体吸入肺中,从而患上呼吸系统疾病。

为了更好地去除矿尘中的各种组分,需要将煤尘、岩尘以及二者混合物进行分类、分选,同时,分质、分级也是煤矿开采过程中不可或缺的一部分[4]。干法选煤技术[5-6]是我国煤炭行业目前正在运用与完善的分类方法,其中细粒煤分选一直是干法选煤技术中的难点之一,现有分类方法仅能实现毫米级粒径的颗粒分类。科氏质量流量计(Coriolis mass flow meter,CMF)可以实现小粒径颗粒的测量,具有测量精度高、介质广、多参数测量、非侵入式测量以及可重复性强等优点[7-11],可实现小粒径细粒煤的参数测量。

目前,研究人员在煤尘和岩尘以及CMF等方面展开了研究。魏存厚等[12]对全断面隧道掘进机工作面的岩尘分布规律进行了数值模拟,研究了协同通风对岩尘扩散的影响;马鹤[13]通过数值模拟与实验测定研究了气载岩尘的运移规律;Ismail等[14]运用流体动力学仿真优化了煤粉分级机模型。Gace等[15]采用双向流固耦合测量单U型管道,实验测量和数值模拟均满足单相水流测量的精度要求。Lu等[16]对气液两相流的流量计进行了动态误差修正。Pei等[17]研究U型管水流对振动特性的影响,发现相位检测器离固定端越远,对应的时滞就会越小。上述CMF测量均针对气液两相流,尚未验证气固两相流的情况,尤其是因为岩尘对人体的危害比煤尘大,所以需要首先分类判别煤尘与岩尘。

岩尘颗粒的粒径≤10 μm,煤尘粒径≤1 mm,为了对微米级煤尘和岩尘混合颗粒进行分类测量,本文中首先建立环形静电传感器模型,根据谐振式U型CMF的测量原理,研究测量管两侧的时间差和流体的质量流量的关系; 依据谐振式U型管道的结构参数选择ANSYS Model软件对谐振式U型测量管进行模态分析,确定CMF的激振频率; 采用双向流固耦合模拟CMF的测量过程,验证利用双向流固耦合及CMF装置对煤尘和岩尘混合颗粒进行分类的可行性; 测量煤尘和岩尘混合颗粒的体积流量,采用谐振式U型CMF测量管测量时间差; 最后采用ANSYS有限元仿真软件对测量管进行静力学分析以及数值模拟分析,验证微米级煤尘和岩尘混合颗粒分类的可行性,实现CMF对煤尘和岩尘混合颗粒的分类。

1 方法

1.1 煤尘和岩尘混合颗粒分类测量示意图

煤尘和岩尘混合颗粒分类测量示意图如图1所示。由图可知,流体从测量管前端入口处流入,经过环形静电传感器与谐振U型科氏流量计后,从测量管后端出口处流出;环形静电传感器可以测量流体的感应电荷量和平均速度,根据流体的流动性原理,可以标定测量管前端的体积流量,谐振式U型CMF测量管可以计算出流体通过该管道时的力学参数与时间差。

1—测量管前端入口; 2—环形静电传感器; 3—谐振U型科氏流量计; 4—测量管后端出口。

1.2 环形静电传感器模型的建立

环形静电传感器的模型最早由文献[18]提出。环形静电传感器几何模型的示意图如图2所示。由图可见,管道外壁接地,电极与管壁绝缘,管壁与电极之间产生的电容忽略不计;环形电极的轴向高度为w,内环直径为D,电极的内环和外环之间的径向厚度忽略不计;点电荷q以速度v沿z轴进行匀速移动,Z为颗粒速度与时间的乘积,Q为极板上的感应电荷量,E为点电荷流动产生的电场强度,x1为点电荷在y轴上的投影与极板中轴线的距离,θ1为积分块与轴线的夹角。

图2 环形静电传感器几何模型示意图

电荷通过环形静电传感器时,设F(x1,θ1)为点电荷到极板间的作用力,则在电极上产生的感应电荷量Q的计算公式[19]为

(1)

(2)

1.3 科氏质量流量测量原理

谐振式U型CMF的测量质量流量原理示意图[20]如图3所示。

(a)测量管结构

由图3(a)—(c)可知,流体从管道的前端流入,流经共振的管道,再从后端流出;当U型测量管内没有流体流动时,测量管将进行相位相同、幅度相同的上下振动,而且测量管道上各点振幅相同;当U型测量管内流体流动时,由于科氏力做功,在振动过程中测量管发生了一定程度的扭转,使得管道前端受到科氏力的遏制,振幅减小,相位滞后。

由图3(d)中的力学分析图中可知,出口与入口的动作方向恰好相反,A侧和B侧之间产生了相位差θ2;测量管平直段的长度为L,弯管的弯曲半径为r,振动角速度为ω,振动偏移量为Δx,扭转角度为θ2。设单位时间内流过测量管的流体质量流量为Qm,则谐振式U型测量管道所受的总扭矩T为

T=(4L+π)rωQm。

(3)

假设整个测量管的等效扭转刚度为K,由于科氏力扭矩的作用是使测量管道发生扭转,扭转角为θ2,并在这个弹性范围内扭转角很小,则由胡克定律可知

T=Kθ2。

(4)

由于管道的对称性以及A、B两侧所受的科氏力大小相同,因此2个监测位置的振动偏移量Δx相同,设A、B两侧输出的时间差为Δt,则振动偏移量Δx计算式为

(5)

综合式(3)—(5),可得质量流量Qm与时间差Δt之间的关系式为

(6)

式中T、L、r皆是由材料本身及管道结构所决定的,为常数。因为质量流量Qm与时间差Δt成正比,所以可以通过测量A、B管两侧的时间差,计算出流体的质量流量。

2 有限元分析

2.1 谐振式U型管道的结构参数

科氏质量流量计的管道种类有很多,谐振式U型管是较早投入市场的管型。相比于直管型,U型管可以降低结构刚度,易于实现振动,不仅可以减小外界干扰,而且能够提高系统整体的品质因数值。市场上CMF产品大多采用谐振式U形管,本文中选择科氏质量流量计中的谐振式U型测量管结构,测量管两边各设置2块减振板,测量管与减振板的材料均设置为316L不锈钢。由于激振器和信号检测器的质量很小,因此建模时将其忽略。谐振式U型管道的结构参数示意图如图4所示。

图4 谐振式U型管道的结构参数示意图

2.2 模态分析

模态是机械结构的固有振动属性,由本身的结构参数和材料属性所决定。每阶模态都有相应的固有频率和振型,识别各阶固有频率和振型的过程称为模态分析。对CMF进行模态分析的目的主要是为了求解管道的固有频率以及各阶振型,然后再以某一振型的固有频率为管道施加激振力,最后根据激振频率进行流固耦合分析。

因为在煤尘和岩尘混合颗粒的分级过程中管道进行上下开合运动,所以需要选取U型测量管近似的模态振型所对应的固有频率,从而确定CMF的激振频率,实现对煤尘和岩尘混合颗粒分级过程的模拟。选择ANSYS Model软件对谐振式U型测量管进行模态分析,谐振式U型测量管前4阶模态振型如图5所示。

(a)一阶振型

由图5可知,前4阶模态振型的固有频率分别为93.6、113.11、163.44、357.41 Hz,一阶振型为两侧管道同时向左或向右进行水平运动,二阶振型为两侧管道同时向外进行开合运动,三阶振型为两侧管道进行交叉水平运动,四阶振型为两侧管道进行扭转运动。因为测量管在无流体流动时受外部激励下的响应需要满足上下开合运动,所以选择二阶振型所对应的固有频率113.11 Hz作为CMF的激振频率。

2.3 双向流固耦合仿真设置

CMF是基于流体与固体相互作用产生的科氏力来测定质量流量的,测量过程是动态变化的,因此采用双向流固耦合来模拟CMF的测量过程。

进行流体模块设置时,湍流模型设为Realizablek-ε,开启欧拉多相流;采用速度入口和压力出口模式,入口速度为5 m/s,出口压力为0;在动网格设置中开启平滑模式,设置2个流固耦合界面;采用全隐式耦合计算方式,相较于半隐式计算,该计算方式的鲁棒性好而且迭代次数少;设置仿真时间为10 min,仿真步长为0.1 s。

进行固体模块设置时,材料选为316L不锈钢,密度为7 850 kg/m3,弹性模量为200 GPa,泊松比为0.3;设置固定约束面、双向流固耦合交互面和激振力;测量管内壁为流固耦合交互界面,激振力的计算公式为

F(t)=F0sin(2πft+θ0),

(7)

式中:F(t)为激振力随时间变化的函数;F0为激振力的幅值;f为激振频率,即二阶振型的固有频率;θ0为初相位。

当流体、固体模块的参数设置完成后,再将二者的计算结果模块连接在系统耦合模块上,在系统耦合模块上设置流体、固体的数据交换区域及顺序,最后点击求解进行双向流固耦合。

2.4 双向流固耦合分析法的验证

流体在测量管中的激振力以压力的形式作用于管道结构,当激振力的频率与测量管道的固有频率一致时,测量管道就会出现共振现象,满足科氏力测量的前置条件。为使双向流固耦合分析结果更加可靠,需要设立2处监测点1、2,以便观察A、B两侧的振动情况,2处监测点振动曲线如图6所示,由图即可得时间差Δt,再由式(6)中即可计算出流体质量流量Qm。

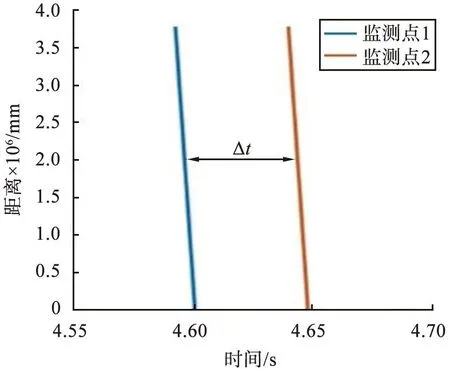
图6 2处监测点的振动曲线

一般情况下,流体质量流量Qm的计算公式为

Qm=ρvA,

(8)

式中:ρ为流体的颗粒密度,A为测量管道截面积,v为流体的平均流速。经式(6)、(8)的计算结果基本相同,说明同一个测量管道入口处的流入速度与测量时间差正相关。

为了验证ANSYS的双向流固耦合分析结果,仿真研究不同流速时所建U型测量管位移所对应的时间差。将仿真数据与文献中的数据进行比对,流速与时间差关系的仿真结果如图7所示。由图可见,相较于文献[21]中的液体水的关系曲线,全岩尘与全煤尘的时间差-流速关系曲线差别较大,但都基本近似于一次曲线,说明流速与时间差成正比;全岩尘的斜率和初始值远大于全煤尘的,即有明显的特征判别参数,从而在理论上验证了可以利用双向流固耦合及CMF装置对煤尘和岩尘混合颗粒进行分类的可行性。

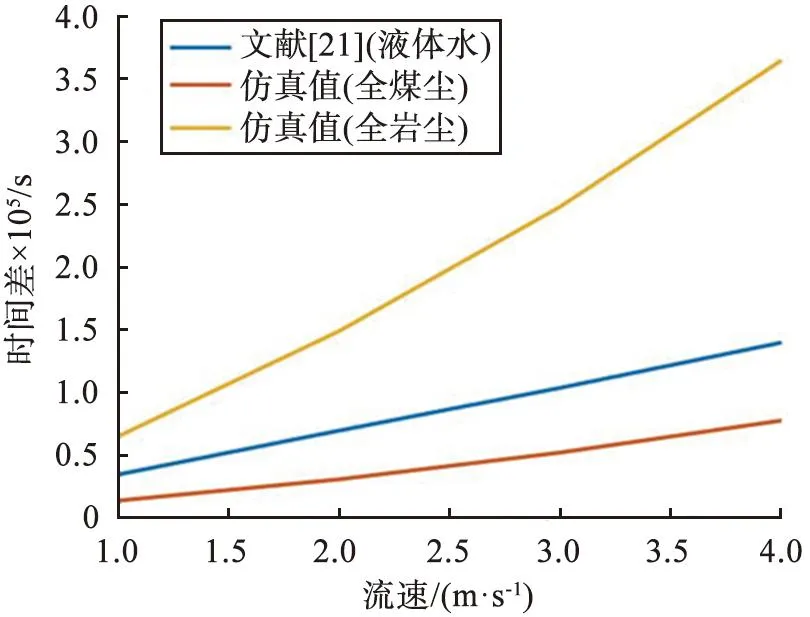
图7 流速与时间差关系曲线的仿真结果

2.5 体积流量的计算

根据流体流动的连续性原理,管道内流体的体积流量Qv的计算公式为

Qv=vA。

(9)

当煤尘和岩尘混合颗粒经过静电感应传感器后,传感器会显示当前流体经过后的电荷量,将式(1)、(2)联立计算便可推出流经该截面(面积为A)的平均速度v;根据式(9)即可测量出经过该管道内流体的体积流量Qv。

3 结果与分析

3.1 颗粒密度与煤尘和岩尘颗粒的力学性能的关系

采用ANSYS Static模块对进行静力学分析,计算出流体的3个力学参数,即最大静压、最大等效应力、总最大形变量,采用双向流固耦合的方式进行时间差的检测,分析颗粒密度与煤尘和岩尘的力学性能之间的关系。煤尘颗粒和岩尘颗粒的力学性能随颗粒密度的变化分别如图8、9所示。

(a)最大静压和最大等效应力

(a)最大静压和最大等效应力

由图8、9可知,煤尘的颗粒密度为0.4～1.0 g/cm3,岩尘的颗粒密度为2.25～2.85 g/cm3,随着颗粒密度的逐渐增大,煤尘和岩尘的最大静压、总最大形变量、最大等效应力等静力学参数以及管道两侧的时间差均呈线性增长,但煤尘曲线的斜率要大于岩尘的。

3.2 粒径不同时煤尘和岩尘混合颗粒的分选

将粒径为10 μm的煤尘颗粒和粒径为1 μm的岩尘颗粒按比例进行混合,煤尘的体积分数从0开始逐渐增大,每次增大10%,直至100%,岩尘则相反,煤尘和岩尘混合颗粒的体积分数之和为100%。分别对全煤尘(以颗粒密度0.6 g/cm3为例)、全岩尘(以颗粒密度2.65 g/cm3为例)以及煤尘和岩尘混合颗粒按体积分数比例混合的3种情况进行模拟分析,计算出各自相应的流体最大静压、总最大形变量、最大等效应力和时间差参数,煤尘和岩尘混合颗粒的力学性能随煤尘体积分数的变化如图10所示。由图可见,煤尘和岩尘按一定比例混合后,流体最大静压、总最大形变量、最大等效应力随煤尘体积分数的增加、岩尘体积分数的减小而逐渐减小,关系曲线近似于直线;煤岩混合颗粒的时间差曲线随煤尘体积分数的增加而减小;与混合颗粒相比,全岩尘、全煤尘的时间差差别很大。综上,粒径不同的煤尘和岩尘混合颗粒的静力学参数和时间差具有鲜明特征。

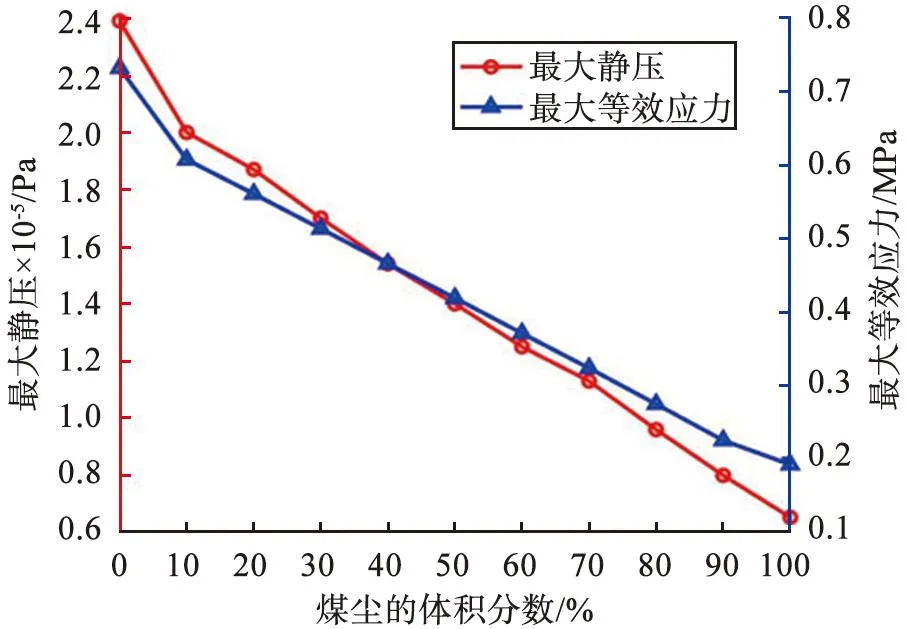
(a)最大静压和最大等效应力

3.3 粒径相同的煤尘和岩尘混合颗粒的分选

将煤尘和岩尘颗粒的粒径设为1、5、10 μm。分别将粒径相同的煤尘和岩尘颗粒进行混合,煤尘的体积分数从0开始逐渐增大,每次增大10%直至100%,岩尘则相反,煤尘和岩尘的体积分数之和为100%。

在各种流体速度条件下,不同粒径的混合颗粒的时间差随煤尘的体积分数的变化如图11所示。由图可知,随着煤尘体积分数的增大,谐振管测量的时间差逐渐减小;对煤尘体积分数来说,测量时间差随着煤尘和岩尘混合颗粒的体积流量的增大而稳步增大;体积流量越大,测量时间差减小的趋势越明显。

不同流体速度时混合颗粒的时间差随煤尘体积分数的变化如图12所示。由图可知,当煤尘体积分数<50%时,粒径为10 μm的混合颗粒的时间差最大,粒径为5 μm的混合颗粒次之。这是因为,混合颗粒中岩尘颗粒体积分数较大,岩尘对测量管道的振动的影响较大,从而使前、后端振动测量曲线的相位差变大。当煤尘的体积分数≥50%时,粒径为1 μm的混合颗粒的时间差最大,粒径为5 μm的混合颗粒次之。这是因为,煤尘颗粒体积分数较大,煤尘的颗粒密度较小,受到的空气阻力较小,而岩尘颗粒所受阻力较大,造成流体流动性变差,岩尘对测量管道的振动产生的影响较小,使得时间差随粒径减小而增大。

(a)速度为1 m/s

综上,煤尘颗粒、岩尘颗粒及其混合颗粒均具有鲜明且不同的分类判别特征,可以采用科氏质量流量计对煤尘和岩尘颗粒实现实时在线精确分类。

4 结论

首先建立环形静电传感器模型,根据谐振式U型科氏质量流量计的测量原理,证明可通过测量管两侧的时间差来计算流体的质量流量;依据谐振式U型管道的结构参数选择ANSYS Model软件对谐振式U型测量管进行模态分析,确定科氏质量流量计的激振频率;采用双向流固耦合模拟科氏质量流量计的测量过程,在理论上验证可以利用双向流固耦合及科氏质量流量计装置对煤尘和岩尘混合颗粒进行分类的可行性;分析颗粒密度与煤尘和岩尘的力学性能之间的关系,研究粒径不同的煤尘和岩尘混合颗粒的静力学参数和时间差随煤尘体积分数的变化,以及粒径相同的煤尘和岩尘混合颗粒随煤尘体积分数和颗粒流速的变化规律。结论如下:

1)在科氏质量流量计的同一个测量管道入口处,颗粒的流入速度与测量时间差正相关。

2)通过模态分析可知,谐振式U型测量管应选择二阶振型所对应的固有频率113.11 Hz作为科氏质量流量计的激振频率。

3)煤尘的颗粒密度为0.4～1.0 g/cm3,岩尘的颗粒密度为2.25～2.85 g/cm3。粒径不同的煤尘和岩尘颗粒混合后,当煤尘颗粒的体积分数增大时,流体最大静压、总最大形变量、最大等效应力和时间差减小; 全岩尘、全煤尘的时间差与混合颗粒的相差较大。粒径相同的煤尘和岩尘颗粒混合后,随煤尘体积分数的增大,时间差急剧减小; 时间差随着混合颗粒的体积流量的增大而增大; 当煤尘体积分数<50%时,粒径越大时间差越大; 当煤尘体积分数≥50%时,粒径越大时间差越小。

煤尘颗粒和岩尘颗粒具有鲜明且不同的分类判别特征,微米级煤尘和岩尘颗粒分类具有可行性,可实现科氏质量流量计对混合颗粒的实时在线精确分类。

利益冲突声明(Conflict of Interests)

所有作者声明不存在利益冲突。

All authors disclose no relevant conflict of interests.

作者贡献(Author’s Contributions)刘丹丹和朱鸿飞进行了方案设计,所有作者均参与了论文的写作和修改。所有作者均阅读并同意了最终稿件的提交。

The study was designed by LIU Dandan and ZHU Hongfei.The manuscript was written and revised by all authors.Both authors have read the last version of paper and consented for submission.