甲烷裂解双分散孔催化剂颗粒积碳行为模拟

王 帅,杨学松,王家兴,2,刘 辉

(1. 哈尔滨工业大学 能源科学与工程学院,黑龙江 哈尔滨 150001; 2.烟台龙源电力技术股份有限公司,山东 烟台 264006)

催化重整技术已广泛应用于制氢行业[1-3]。催化重整过程中积碳不可避免,大大影响了催化剂颗粒的性能和制氢效率[4]。积碳会覆盖活性位点,同时催化剂颗粒内部孔隙结构会因形成的积碳而变窄甚至堵塞,从而增大扩散阻力[5],因此,深入认识积碳行为对于催化剂颗粒设计与重整制氢过程调控具有重要意义。

关于积碳问题,开发高反应性和抗积碳型催化剂是重要的研究目标[6-8]。Dan等[9]制备了双峰孔结构催化剂。研究表明,大孔有助于试剂更好地靶向催化活性中心,二氧化铈更好地保留了双峰多孔结构并减少约70%的碳沉积。随着多孔材料可控合成技术的发展,研究者不再满足于经验改性,转向将催化剂颗粒微观孔隙结构与反应-传质过程通过数学模型关联起来,指导催化剂设计和优化[10]。Zhu等[11]集成了质量、动量和热平衡方程、空间孔径和孔隙率分布模型、多组分扩散和集总动力学模型,模拟研究了孔径分布和孔隙率对甲醇制烯烃中多孔催化剂颗粒内扩散和反应特征的影响。结果表明,催化剂孔径和孔隙率从颗粒表面向颗粒核心减小是最佳的孔隙分布。孔径越小,产物中乙烯与丙烯的比例越大。Ye等[12]将孔网络模型用于研究单一催化剂颗粒积碳行为。研究发现,失活过程可以分为2个阶段,后期形成的焦炭要比前一阶段更多。Lin等[13]采用改进的随机生成大孔算法构建了催化剂结构,基于格子玻尔兹曼模型,研究了甲烷干重整催化剂中大孔与小孔的体积比和孔径比等参数对积碳和催化性能的影响。增加催化剂孔隙率和大孔与小孔的直径比可以增强颗粒内扩散,但减少了催化剂孔的总表面积。

尽管在颗粒积碳行为与多分散颗粒设计上,国内外学者开展了相关研究工作,但对于积碳导致孔隙结构演变与反应性能失活的耦合规律的研究较少,难以全面理解积碳效应下催化剂界面反应传质特性。本文中基于颗粒解析模型,考虑积碳引起的孔隙结构动态演变以及反应性能的衰减,构建传质与反应活性全耦合的颗粒尺度模型,对甲烷裂解中催化剂颗粒的积碳行为开展模拟研究,比较单分散孔颗粒(初始孔隙率为0.6,孔径为2 nm)和双分散孔颗粒(大孔和小孔的孔隙率均为0.3,孔径分别为1 000、2 nm)积碳行为下孔隙结构演变特性,获得固定床反应器积碳分布规律,为催化剂颗粒设计开发提供理论指导。

1 数学模型

1.1 控制方程

将催化剂颗粒视为多孔介质,颗粒内部物质扩散与反应过程可以通过自定义反应源项表示。连续性方程与动量方程[14]为

(1)

(2)

式中:ε为颗粒孔隙率;ρ为密度;t为时间;u为气体速度;Sm为反应引起的质量变化量;p为压力;μ为气体黏度;κ为多孔介质颗粒的渗透率。

物质输运方程[15]表示为

(3)

(4)

(5)

(6)

(7)

对于双分散孔颗粒,由于孔径差异,因此比表面积被用来计算反应速率。假设孔径为圆柱形结构,比表面积计算[18]可以表示为

(8)

式中:S为表面积;Vcat为体积;dma为大孔孔径;dmi为小孔孔径。

能量守恒方程为

(9)

式中:(ρCp)eff为有效热容;T为温度;keff为有效导热系数;Q为反应热。

催化颗粒外的区域视为自由流动区域,控制方程[14]为

(10)

(11)

(12)

(13)

1.2 反应模型

采用甲烷裂解来探究积碳失活对催化剂颗粒催化性能的影响。采用Zavarukhin等[19]的动力学模型,具体表达式为

CH4↔C+2H2,

(14)

(15)

(16)

(17)

(18)

式中:rc为反应速率;kc、kH、kp为速率因子;PCH4为甲烷分压;PH2为氢气分压;Rg为气体常数。

考虑比表面积的影响,将反应速率折算成表面反应速率。考虑积碳引起的活性变化,积碳生成速率[19]可表示为

reff=α·rs,c,

(19)

式中:rs,c为甲烷裂解反应速率;α为反应活性。活性动力学模型[19]为

(20)

(21)

式中:ka为速率因子;c为积碳负载量。孔隙率随积碳速率的变化[14]可描述为

(22)

式中:MC为积碳摩尔质量;ρc为积碳密度。

1.3 模拟对象与边界条件

图1所示为催化剂颗粒与固定床反应器结构。催化剂分别为单分散孔颗粒和双分散孔颗粒,粒径为5 mm,密度为3 980 kg/m3。底部为速度入口,进气燃料为甲烷,速度为0.1 m/s,进口热力学温度为923 K,出入口的一段距离内未填充载氧体颗粒,以减小出入口对于流动过程的影响。反应器顶部为压力出口,压力为0.1 MPa,对于壁面,采用无滑移绝热条件。

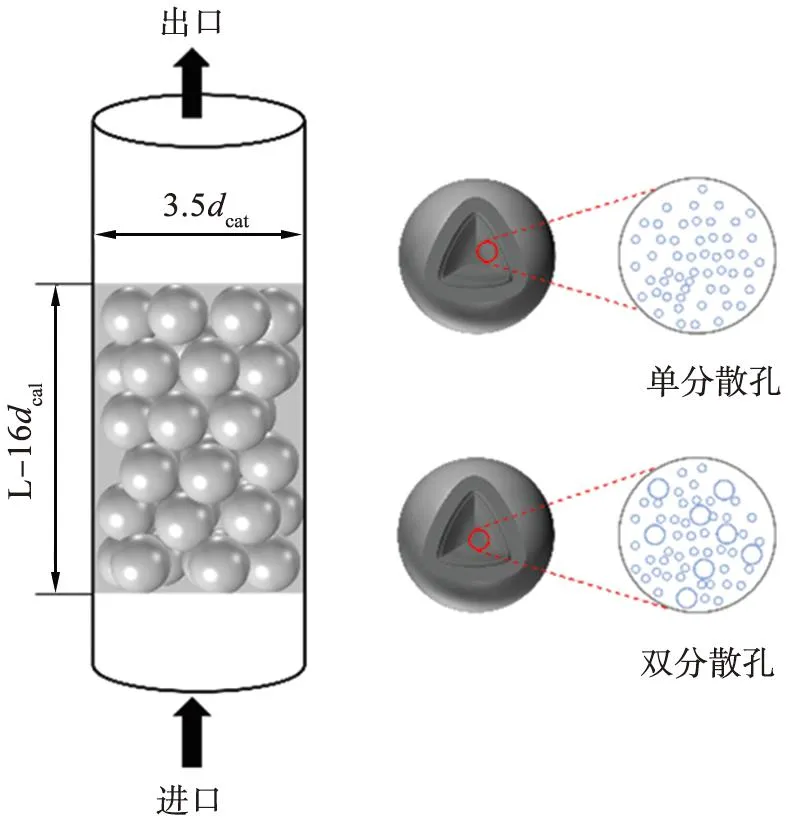
注:dcat为催化剂的粒径。

1.4 模型执行与模型验证

本研究模拟基于Comsol软件平台,利用有限元方法求解。模拟时间为10 000 s,组分和能量守恒的最大允许误差为0.000 1,其余参数为0.001。本文中选择的反应模型在之前的研究工作中已得到了实验验证[14],可以较好地描述甲烷裂解和积碳形成。图2所示为模型验证与网格无关性分析。为了验证固定床模型的可行性,将不同雷诺数条件下相对压降与文献[20]中Eisfeld-Schnitzein的经验关联式作对比,如图2(a)。可以发现,模拟值和经验式获得的值具有较好的一致性,模拟具有一定的可行性。图2(b)给出了固定床网格无关性分析。从中可看出,中等网格和细网格差异不是很明显,考虑到计算精度与效率的影响,选取中等网格进行模拟。

(a)压降验证

2 结果与讨论

2.1 单个颗粒积碳反应-扩散特性

单分散孔和双分散孔颗粒的氢气浓度分布瞬态变化如图3所示。由于催化剂颗粒积碳失活,氢气浓度随着时间推移而降低。对于单分散孔颗粒,初始阶段会存在氢气浓度的上升段,这与反应扩散的协同控制有关。由于单分散孔颗粒的扩散系数较小,反应产生的氢气被累积,因此导致浓度增大。随着反应速率的降低和积碳的形成,氢气浓度下降。相较于单分散孔颗粒,双分散孔颗粒的扩散阻力小,氢气浓度分布的均匀性得到提高。

图3 单个颗粒中氢气浓度的瞬态变化

单个颗粒的积碳量瞬态变化如图4所示。催化剂颗粒内积碳量随着反应进行不断增加。由于本征活性因子降低和传质阻力增大,积碳生成速率逐渐降低至失活,导致积碳量达到最大沉积量。从空间分布上可以发现,积碳首先沉积在壳层区域,向核心区域逐渐减少。随着积碳的不断生成,核心区积碳量更加显著。单分散孔颗粒的壳层区2 000 s左右积碳量达到最大值,而后趋于稳定,说明壳层提前失活;中心区域,在5 000 s左右才趋于失活。较于单分散孔颗粒,由于双分散孔颗粒具有较小的扩散阻力,其积碳空间分布也更加均匀,所达到的最大积碳量也明显增加,这意味着双分散孔颗粒的失活时间延长,在10 000 s左右仍旧可以继续产生积碳,说明双分散孔颗粒的抗积碳能力增强。

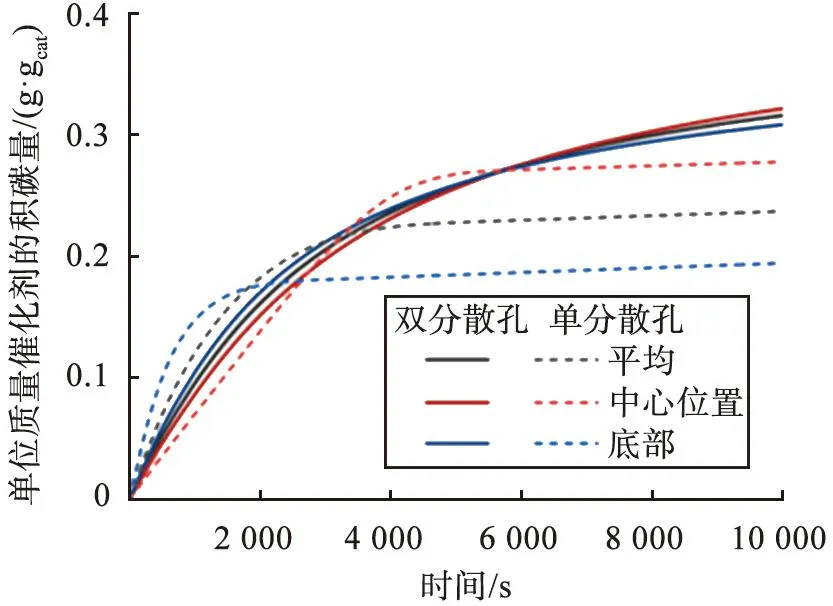
图4 单个颗粒积碳量的瞬态变化

单个颗粒中反应速率瞬态变化如图5所示。由于催化剂活性因子的降低和扩散阻力的增大,单分散孔和双分散孔颗粒的反应速率随时间的推移而下降。开始时,单分散孔和双分散孔颗粒核心区反应速率低于壳层区反应速率,随着积碳的不断产生和催化活性因子的减少,壳层区反应速率的下降程度变得更加明显,导致核心区反应速率大于壳层区域。由于双分散孔颗粒与单分散孔颗粒相比具有更小的内扩散阻力,反应速率的衰减程度受到抑制,因此积碳速率的空间分布更加均匀。相比之下,单分散孔颗粒速率的衰减程度更快,扩散系数较小导致颗粒中心和壳层的反应速率差异也较大。

图5 单个颗粒中反应速率的瞬态变化

图6所示为单个颗粒的有效扩散速率。由图可知,初始阶段,有效扩散系数随着反应的进行而不断减小,核心区扩散系数大于壳层区的。随着积碳的不断生成,壳层区扩散速率大于核心区的。相较而言,双分散孔颗粒的有效扩散速率始终大于单分散孔颗粒的,随着积碳的不断生成,双分散孔颗粒的扩散速率不均匀分布程度也低于单分散孔颗粒的,说明双分散孔颗粒中大孔的引入,促进了壳层向核心处的气体扩散,对由局部堵塞导致催化剂失活起到了抑制作用。

图6 单个颗粒的有效扩散速率

2.2 固定床反应器颗粒积碳分布与孔隙结构演变特性

为了更好地认识固定床反应器中流动特性与积碳行为之间的关系,图7所示为固定床反应器内速度与积碳量的瞬时分布云图。当气体流经催化剂颗粒间孔隙通道时,形成一些局部的高流速区域,传质和反应过程得到加强,产生局部高积碳量区域,表明催化剂颗粒在固定床中的分布将直接影响催化剂的活性变化。

(a)速度

固定床径向床层孔隙率和流动特性呈现不均匀分布。固定床壁面附近的床层孔隙率最大,导致催化剂颗粒的催化性能也发生变化,即固定床壁面效应。为了评估壁面效应,图8所示为固定床平均积碳量、活性因子和床层孔隙率的瞬时变化,其中局部孔隙率、活性因子和积碳量是通过不同径向圆环面加权平均值计算的。

(a)积碳量

由图可知,壁面效应导致床层内的局部孔隙率增加,引起局部流速增大,促进了传质过程,导致局部更多的积碳形成,从而大大减少了催化剂活性因子的数量。过小的长径比会导致壁面效应更显著,因此,合适的长径比对于抑制床层壁面效应与积碳是至关重要的。

3 结论

基于颗粒尺度模型,耦合反应动力学模型,开展了甲烷裂解中多孔催化颗粒积碳行为的模拟研究,比较了单分散孔颗粒与双分散孔颗粒积碳行为及其所引起的孔隙结构演变特性,探究了固定床反应器壁面效应对积碳行为的影响。

1)积碳失活从多孔颗粒表层向内部核心移动,在积碳失活初期,壳层区反应速率较大,随着积碳的不断生成,核心区反应速率占主导地位,壳层与核心区反应速率数值发生反转。

2)相较于单分散孔颗粒,双分散孔颗粒具有较低的扩散阻力,积碳空间分布更加均匀,最大积碳量也明显增大,双分散孔催化颗粒具备更强的抗积碳性能。单分散孔颗粒在5 000 s左右才趋于失活,双分散孔颗粒在10 000 s左右仍可以继续反应。

3)整个固定床反应器中床层积碳分布不均匀,壁面附近传质系数较大导致催化颗粒失活更加严重。

利益冲突声明(Conflict of Interests)

所有作者声明不存在利益冲突。

All authors disclose no relevant conflict of interests.

作者贡献(Author’s Contributions)

王帅、杨学松、王家兴、刘辉参与了数值模拟、论文的写作和修改。所有作者均阅读并同意了最终稿件的提交。

The study was designed by WANG Shuai,YANG Xuesong,WANG Jiaxing and LIU Hui.The manuscript was drafted and revised by WANG Shuai,YANG Xuesong,WANG Jiaxing and LIU Hui.Both authors have read the last version of paper and consentedfor submission.