多向角焊缝连接矩形钢管的抗弯特性研究

史云中　王志宇　何明德　祝轲

摘要：多向角焊缝是角焊缝的重要组成部分，目前对角焊缝研究主要集中于单向角焊缝，较少涉及到均由斜向角焊缝组成的多向角焊缝，因此，本文以福州地铁6号线营前站幕墙龙骨节点为工程背景，设计制作3根多向角焊缝试件，采用有限元软件建立试件同类型模型，再考虑焊缝长度及段数等因素，基于CSA S16-14规范提出的多向角焊缝强度折减系数，推导出正应力和剪应力组合作用下组合应力理论计算公式。结果表明：合理加长中连接板和焊缝长度会降低延性，但对于提高承载力效果显著，约为0.8～2.5倍；合理的焊缝倾斜角度和焊脚尺寸等参数对此类结构跨中截面承载力有影响，相比而言后者的影响更显著；多向角焊缝与单向角焊缝形态和受力上存在差异。本文研究结果表明对多向角焊缝的研究具有重要意义，多向角焊缝的研究能为工程节点设计及安全性分析提供理论基础和指导。

关键词：角焊缝；多向焊缝；受弯承载力；组合应力；延性

中图分类号：TU511.3;TU391文献标志码：A文献标识码

Study on the bending behavior of rectangular steel tubes connected by multi-orientation fillet welds

SHI Yunzhong1，WANG Zhiyu1*，HE Mingde2，ZHU Ke2

（1 Department of Civil Engineering，College of Architecture and Environment，Sichuan University，Chengdu，Sichuan 610065，China; 2 The Architectural Decoration Engineering of China Railway Erju Group，Chengdu，Sichuan 610031，China）

Abstract：Multi-orientation fillet weld is an important part of fillet weld.The multi-orientation fillet welds composed of oblique fillet welds have been less focused than uni-orientation fillet welds in current research work.Taking the curtain wall keel node of Yingqian station of Fuzhou Metro Line 6 as the engineering background，therefore，three specimens of multi-orientation fillet welds were designed and fabricated.The specimens of identical configurations and considering the factors such as weld length and number of segments were also established using finite element software.Based on the strength reduction coefficient of multi-orientation fillet weld proposed in CSA S16-14 specification，the theoretical calculation formula of combined stress under the combined action of normal stress and shear stress was deduced.It has been found that the ductility is reduced with extended middle connecting plate and weld length，but the bearing capacity is significantly improved about 0.8～2.5 times.The bearing capacity of mid span section was influenced by not only the weld inclination angle but more notably the weld leg size.Given the differences exist in shape and stress between multi-orientation fillet weld and uni-orientation fillet weld，the research on multi-orientation fillet weld is of great significance while it can provide theoretical basis and guidance for engineering joint design and safety analysis.

Key words： fillet weld;MOFW;bending capacity;combined stress;ductility

曲面矩形鋼管结构因不规则造型，其节点可能由多条不同角度的斜向角焊缝组成的多向角焊缝连接，例如福州地铁6号线营前站多曲面幕墙龙骨节点。多向角焊缝与普通角焊缝形态和受力上存在区别并且几何形态复杂，计算和设计方法不能直接沿用普通角焊缝计算方法，但多向角焊缝节点在实际工程应用更多［1］，对该节点的研究具有重要理论意义和工程应用价值。

多向角焊缝节点在搭接板转角处常常是连续施焊，目前，国内外对围焊类角焊缝研究较为成熟。FU G M等［2］研究表明焊接的顺序直接导致板间焊缝起始与结束附近的残余应力发生改变，横向残余应力受此影响较大，其他区域受的影响反而不大；ZHU L等［3］发现当强度不匹配时，母材强度高会使焊缝塑性区受抑制而局限在焊缝附近区；DENG D等［4］发现采用单道焊和多道焊焊接顺序的试件横向残余应力沿表面、厚度方向有剧烈变化，应力值发生显著变化；王新峰［5］等对轴向力下三面围焊研究发现正面焊缝应力高于侧面焊缝应力，正面焊缝应力沿焊缝长度对称分布，基板侧焊趾处应力及连接板焊根处应力大；宁磊［6］发现三面围焊角焊缝焊趾处应力值最高，应力集中系数随板厚增加而减小，板厚增加一定程度后系数趋于稳定，应力集中系数随角钢厚度增加而增加，加大焊脚尺寸系数下降；孙红［7］通过受拉试验分析多向角焊缝节点力学性能，考虑包括韧性不兼容影响、焊缝段长度和焊缝段间相互作用在内的若干因素对多向角焊缝节点受力性能的影响，最终导出多向角焊缝节点承载力设计表达式；曹瑞泽［8］基于钢框架盖板加强型节点试件的单调拉伸试验研究焊缝的断裂行为，发现试件出现梁翼缘颈缩变形断裂及加强板端部角焊缝脆性断裂破坏现象；施刚［9］从微观断裂力学角度研究Q460 钢角焊缝搭接接头断裂行为并进行有限元分析，有限元模型中采用试验标定的断裂参量，可有效地预测正面角焊缝破坏行为，得出延性起裂荷载（极限承载力状态）；张有振等［10］、杨璐等［11］基于双相型S22053与奥氏体型S30408不锈钢正、侧面角焊缝连接试件拉伸试验研究角焊缝受力性能，结果表明正面角焊缝呈约30°不规则撕裂破坏，侧面角焊缝断裂破坏呈45°平整裂状，正面角焊缝抗拉强度是侧面角焊缝剪切强度1.47倍。

目前，各国的钢结构设计规范主要是针对单向角焊缝，并给出了设计方法，而针对多向角焊缝的很少，如加拿大钢结构规范CSA S16-14采用多向角焊缝强度折减系数来考虑焊缝段之间相互作用的影响，另外，现有的规范和文献［7］仅考虑了剪切应力或拉应力，并且只针对强度得出了计算公式，并未考虑延性等其他受力性能。因此，本文针对包括焊缝长度、段数等两类构造的多向角焊缝试件开展静载受弯试验，研究由斜向角焊缝段组成的多向角焊缝受力特性，并通过试验对有限元分析结果进行验证，研究焊缝倾斜角度和焊脚尺寸等参数对其正截面强度的影响，验证正截面强度计算理论的准确性，旨在为保证适应于钢管组合梁及其它组合结构的焊接连接可靠性提供理论基础，以及进一步确定连接等部位损伤发展、疲劳应力特性和破坏模式分析提供数据支持。

1 试验概况

1.1 试件设计

本文参照GB 50017—2017《钢结构设计规范》及EN 1993欧洲规范3设计3根试件，试件材料均采用Q355B钢材，焊缝焊条采用E50型，采用CO2作保护气体。

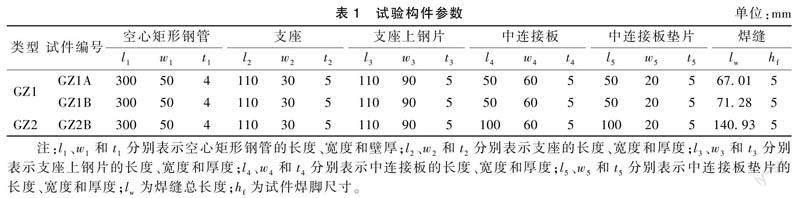
3根试件分为2种构造类型GZ1和GZ2，GZ1类型试件包含2根尺寸构造相同的试件GZ1A、GZ1B，試件参数见表1。

1.2 测点布置

在水平矩形钢管距离支座30、200、305mm布置量程±100mm、分辨率0.01mm的位移传感器（以下简称位移计）1、2、3，测定钢管位移值，测点见图1a、图2a；在倾斜的矩形钢管上布置应变片，测定受力过程中钢管的应变值，由静态应变采集箱采集，GZ1和GZ2在焊缝长度接近钢管边长面上的2个三等分点布置4个应变片，同一水平线的2个应变片距离焊趾分别为0.5t1和1.5t1，t1为空心矩形钢管壁厚；较短焊缝面上焊缝长度的2个三等分点错位布置2个应变片，2个应变片距离焊趾分别为0.5t1和1.5t1，t1为空心矩形钢管壁厚，测点布置见图3。

1.3 加载方案

采用电液伺服试验机对试验试件施加跨中集中荷载（图6）。正式加载前先完成预加载，以消除各部位安装连接间隙，并测试装置工作是否正常;试验中采用分级递增加载，采用位移控制加载过程，直至试件破坏或荷载降到0.85倍极限荷载时结束试验。

2 试验结果及分析

2.1 试件破坏及裂纹开展模式

GZ1和GZ2试件的试验现象类似，主要过程如下：随着荷载的增大，试件逐渐进入弹塑性工作阶段，表现为跨中焊缝附近钢梁表面的锈皮脱落；随后位于焊缝截面最底部的最不利焊点先被拉裂，焊缝逐渐被拉裂，中连接板与正放钢管底部焊缝也出现裂缝，受压区焊缝少量裂纹产生，中连接板底部裂缝和受拉区裂缝持续开裂；当加载至极限荷载时，在正应力和剪应力的组合作用下，焊缝裂缝迅速向上发展，最终导致试件破坏。不同的是，GZ2类型试件由于中连接板和焊缝长度更长，扭转效应更明显。

2个试件焊缝破坏形状见图7。

2.2 荷载-位移曲线分析

加载过程中试件跨中截面荷载-位移曲线（图8）显示：GZ1试件的荷载-位移曲线呈现四折线特征，加载初期曲线靠近纵轴，近似呈线性关系。当加载至约1.5 kN时，图形由近似直线变为曲线，出现第1个转折点，这是由于焊缝弹性阶段结束，焊缝开始小部分出现不可逆破坏造成的。继续加载至5 kN附近，曲线出现第2个转折点，在这一阶段，由于焊缝下部受拉区焊缝已经屈服，塑性应变和跨中加载位移增大而焊缝应力基本维持不变，在荷载-位移图上大致是一条水平线，形成类似于“塑性铰”之类的结构，即试件在达到极限荷载后，荷载的变化虽小，但跨中截面位移增量却很大，这意味着在截面承载力没有明显变化的情况下，具有较大的变形能力，即具有较好的延性。此阶段过后，部分焊缝达到极限应变，开始退出工作，中性轴向上移动，试件跨中发生相同位移，所需要的力越来越小，荷载-位移曲线开始下降。GZ1A和GZ1B的最大承载力分别为5.08、5.13 kN，由于焊缝质量不同，GZ1B试件的“塑性铰”阶段位移增加较小就结束了，即GZ1A试件延性好于GZ1B试件。

对GZ2B进行相同的静力加载试验，测得GZ2B的最大荷载为9.49 kN，与没有中连接板而只是在空心矩形钢管接触点采用对接焊缝的GZ0最大承载力比值约为3.39，但GZ2B“塑性铰”时期更短，延性小于GZ1类型试件，GZ2B与GZ1试件的最大承载力比值约为1.86。原因分析如下：GZ2试件焊缝总长度lw约为GZ1试件的2倍，在加载方式和焊缝质量无明显差异情况下，由于GZ2B中连接板较长，扭转效应虽然更明显，但扭转应力是出现在矩形中连接板的长边和短边中点，只对个别焊点影响较大，但对整体承载力无较大影响。

3 试件受弯承载力理论分析

3.1 计算假定

（1）在集中荷载下，焊缝截面受力满足平截面假定［12］；钢材和焊缝本构关系参照理想弹塑性应力-应变关系。

（2）GZ1类型试件将焊缝分解成2段，2段焊縫长度与空心矩形钢管边长w1的关系为：w1=la，lb=la·tanθ，并令S=1+tan（0.5θ）、M=sinθ-cosθtan（0.5θ）、N=cosθ+sinθtan（0.5θ）D=0.7hfla3、C=1.4hfla、Q=FLla，Z1=1+0.5sin1.5θ、Z2=1+0.5cos1.5θ、X1=0.85+θ/600、X2=0.85+（0.5π-θ）/600，参数见图2。

（3）GZ2类型试件将焊缝分解成4段，4段焊缝长度与空心矩形钢管边长w1的关系为：w1=lab=lad，lbe=lab·tan（45-0.5θ），ldg=lab·tan（0.5θ），并令S=2+tan（45-0.5θ）+tan（0.5θ）、N=11+cosθ+tan（45-0.5θ）、M=1-tan（0.5θ）+tan（45-0.5θ）-（tan（45-0.5θ））2、C=1.4hflab、Q=FLlab、D=（0.7hflab3）/24、Z1=1+0.5sin1.5θ、Z2=1+0.5cos1.5θ、X1=0.85+θ/600、X2=0.85+（0.5π-θ）/600，参数见图4。

（4）不考虑人为施焊等因素对焊脚尺寸及焊缝质量的影响，焊脚尺寸hf两种构造试件都相同且为定值；剪应力由焊缝均匀承担且不考虑构件整体扭转效应。

3.2 组合应力

在求解焊缝截面组合应力之前需求得焊缝截面对于其形心的惯性矩，由于焊缝较复杂，不能直接计算，根据惯性矩的定义可知，组合截面对于某坐标轴的惯性矩等于其各个组成部分对于同一坐标轴的惯性矩之和［13］，如前文假设，将焊缝分段分别求惯性矩，再求和。

多向角焊缝需要考虑韧性不兼容影响和焊缝段之间相互作用的影响，不能把各焊缝段的极限承载力直接相加［14］。故本文剪应力的计算根据提出多向角焊缝强度折减系数的CSA S16-14规范中的公式进行计算：

式（1）中θ为焊缝段轴线与荷载作用线夹角；Aw为焊喉面积；Фw为安全系数，针对焊接金属取0.67；Xu为焊缝金属屈服强度；Mw为多向角焊缝强度折减系数，表达式为Mw=（0.85+θ1/600）/ （0.85+θ2/600），θ1为目标焊缝角度，θ2为两段焊缝在连接处最接近90°的角度。使用Mw修正每段焊缝的面积，然后在求和得出焊缝焊喉总受剪面积，利用截面剪力与剪应力之间的线性关系求出焊缝所受剪应力。

以下为GZ1试件受压区最不利点A应力，由图3可知，2段焊缝的θ2均为90°，基于假设其正应力和剪应力如下：

4 有限元分析

4.1 有限元软件及参数设置

为验证本文所提出的正截面强度计算理论，采用Midas FEA v3.7.0软件建立2组不同构造模型。计算跨度为0.605m，梁端为铰接支承，网格划分采用自动实体网络。参照文献［15］，焊缝远离区网格最大尺寸设为10mm，仅进行粗略划分；中间部分网格尺寸设为5mm；因焊缝附近应力改变较为明显，网格最小尺寸设为3mm，如图9所示。应力云图如图10所示，可见，2种构件应力最大位置与之前分析的理论最不利点一致；最不利点的最大应力约为相邻截面同一部位平均应力的2～2.5倍，即焊缝最不利点处存在显著的应力集中现象；两种构造试件的中性轴位置不同，GZ2试件的受压区高度小于GZ1试件。不同模型参数（跨中荷载）下应力模拟值与试验值结果见表2和表3。

由表2、表3可以看出试验、模拟、理论几者吻合较好，这验证了试验研究、理论分析和模型参数分析三个部分的正确性。

4.2 模型验证

为研究焊缝倾斜角度和焊脚尺寸对多向角焊缝正截面强度的影响，不同倾斜角度（15°～60°）和不同焊脚尺寸（4～7mm）在3kN集中荷载下理论值与模拟值结果（拉正压负）见表4至表7，理论值与模拟值对比如图11所示。

由表4至表7中的应力模拟值可知：焊脚尺寸和在一定范围内倾斜角度的增大对降低焊缝的应力水平均有一定作用。焊脚尺寸的变化对中性轴的位置无影响，只会改变惯性矩，而倾角的变化会引起中性轴位置和惯性矩的改变，由此出现焊脚尺寸增大对降低焊缝平均拉应力水平的效果优于角度改变的现象。随着焊脚尺寸的增大，受拉区和受压区最不利点附近应力降低的程度逐渐减小，在图11中表现为图形斜率逐渐减小。焊缝截面的理论值与模拟值吻合较好，误差原因主要在于理论分析中为了在实际工程中应用方便，所以尽可能减少参数，以及建模和理论计算模型的细微差距，导致两者中性轴位置不一致而产生误差。

4.3 与其他公式对比

选取文献［7］中TF节点公式进行对比分析，其中文献［7］的试验选用了包含正面角焊缝的多向角焊缝试件，在公式推导中将正面角焊缝选为关键焊缝段，仅考虑了试件受拉，并未考虑CSA S16-09就提出的多向角焊缝强度折减系数。本文的试验选用受弯试验，能同时考虑焊缝受拉和受压，试件选用由斜向角焊缝构成的多向角焊缝试件，公式则基于CSA S16-14提出的多向角焊缝强度折减系数进行推导，应用范围更广，可以适用于不同的节点构造。针对本文试验结果，通过其他公式计算不同荷载下应力，结果如图12所示。

由图12可知：GZ1试件所得结果整体上呈现一致的规律，即随荷载的增加，应力也都近似呈线性增大。试验值与本文公式计算值的平均比值为1∶1.08，比文献［7］公式和强度相加法的精度平均提高约8.05%和11.90%。GZ2与GZ1试件相比，焊缝更长同时焊缝缺陷也更多，部分焊缝很快就退出工作，所以导致试验值大于各计算方法所得结果。试验值与本文公式值的平均比值为1∶0.85，相比文献［7］公式和强度相加法精度平均提高了约15.08%和10.67%。

5 结论

（1）多向角焊缝连接板和焊缝长度的增大可有效增大抗弯承载力，同时焊缝缺陷会更多，导致延性较差及整体扭转效应更明显。

（2）随着倾斜角度增大，焊缝受拉区最不利点附近拉应力会先减小后增大；增大焊脚尺寸能降低多向角焊缝的应力水平，但其对应力影响会逐漸减小；相比而言，增加倾角不如适当增大焊脚尺寸能有效降低节点拉应力。

（3）本文提出的多向角焊缝组合应力计算公式具有较高的精度，且在实际使用荷载状态下有约20%的安全储备，并与有限元参数分析结果验证良好，可为实际工程设计提供一定参考。

参考文献（References）

［1］韦逢.端缝加强型三面围焊角焊缝连接受力性能研究［D］.广州：广州大学，2020.

［2］FU G M，MARCELO I L，DUAN M L，et al.Influence of the welding sequence on residual stress and distortion of fillet welded structures［J］.Marine Structure，2016，46：30-55.

［3］ZHU L，TAO X Y.The study of weld strength mismatch effect on limit loads of partsurface and embedded flaws in plate［J］.International Journal of Pressure Vessels and Piping，2016，139-140：61-68.

［4］DENG D，KIYOSHIMA S，OGAWA K，et al.Predicting welding residual stresses in adissimilar metal girth welded pipe using 3D finite element model with a simplified heatsource［J］.Nuclear Engineering & Design，2011，241（1）：46-54.

［5］王新峰，唐琰，刘军.基于ANSYS的三面围焊直角焊缝应力分析及焊缝长度比例优化［J］.焊接技术，2015，44（1）：69-73.

WANG X F，TANG Y，LIU J.Stress analysis and weld length proportion optimization of three-side welding right angle weld based on ANSYS［J］.Welding Technology，2015，44（1）：69-73.

［6］宁磊，雷宏刚，闫亚杰.钢结构三面围焊直角焊缝应力集中的有限元分析［J］.中国科技论文，2018，13（1）：98-102.

NING L，LEI H G，YAN Y J.Finite element analysis of stress concentration at right-angle welds of three-side welded steel［J］.China Sciencepaper，2018，13（1）：98-102.

［7］孙红.多向角焊缝节点受力性能和设计方法研究［D］.西安：西安建筑科技大学，2012.

［8］曹瑞泽，刘芸，吴天祥，等.盖板加强型节点局部试件断裂性能试验研究［J］.广西大学学报（自然科学版），2019，44（4）：977-987.

CAO R Z，LIU Y，WU T X，et al.Experimental investigation on fracture performance of beam-cover-plate reinforced connection of partial specimen［J］.Journal of Guangxi University（Nat Sci Ed），2019，44（4）：977-987.

［9］施刚，陈玉峰.高强度钢材焊缝连接试验研究［J］.工业建筑，2016，46（7）：47-51.

SHI G，CHEN Y F.Investigation on high strength steel welded connections［J］.Industrial Construction，2016，46（7）：47-51.

［10］张有振，杨璐，周晖，等.双相型不锈钢角焊缝连接承载性能有限元分析［J］.工程力学，2017，34（9）：110-118.

ZHANG Y Z，YANG L，ZHOU H，et al.Finite element analyses of loading capacity of fillet-weld connections fabricated from duplex stainless steel［J］.Engineering Mechanics，2017，34（9）：110-118.

［11］杨璐，张有振，周晖，等.奥氏体型S30408不锈钢角焊缝连接拉伸试验研究［J］.建筑结构学报，2017，38（2）：48-54.

YANG L，ZHANG Y Z，ZHOU H，et al.Tensile test on fillet weld connections of austenitic stainless steel grade S30408［J］.Journal of Building Structures，2017，38（2）：48-54.

［12］曾祥英，吴光文，雷明，等.上层建筑薄板焊接变形控制研究［J］.船舶工程，2020，42（S1）：409-414.

ZENG X Y，WU G W，LEI M，et al.Research on welding deformation control of super structure thin plate［J］.Ship Engineering，2020，42（S1）：409-414.

［13］張敏，李百建.波纹钢板截面几何性质计算［J］.科学技术与工程，2012，12（10）：2400-2403.

ZHANG M，LI B J.Calculation of geometric properties of corrugated steel platesection［J］.Science Technology and Engineering，2012，12（10）：2400-2403.

［14］周苗倩.局部加强的三面围焊角焊缝连接受力性能研究及参数分析［D］.广州：广州大学，2018.

［15］钟雯，丁幼亮，王立彬，等.Q370qE钢桥面板顶板-纵肋焊接残余应力试验研究［J］.东南大学学报（自然科学版），2018，48（5）：857-863.

ZHONG W，DING Y L，WANG L B，et al.Experimental study on welding residual stress of Q370qE steel deck deck-rib［J］.Journal of Southeast University（Natural Science Edition），2018，48（5）：857-863.

（责任编辑：编辑张忠）

收稿日期：2021-11-01

基金项目：四川省科技计划（2020YJ0307）

作者简介：史云中（1996—），男，硕士研究生，专业方向为组合结构研究，e-mail：syz566318@163.com。

*通信作者：王志宇（1980—），男，副教授，从事组合结构研究，e-mail：zywang@scu.edu.cn。