基于耳切法的三维模型区域标绘

韩晓明，冯孟奇，褚飞黄，白瑞婷

（国能数智科技开发（北京）有限公司，北京 100011）

三维综合集成展示系统项目在当前的安全监控领域中具有重要的应用价值。为了实现对设备的有效管理和监控，准确而高效的区域标绘与设备框选技术成为项目中的关键环节。然而，现有的安防标绘方法和设备框选技术在处理复杂场景、准确性和效率等方面仍然存在一定的挑战。耳切法作为一种经典的计算几何算法[1]，通过用户标记的方式，可以构建出精确的区域模型来框住设备，同时具有较高的计算效率。本文将探索如何将耳切法应用于智能安防项目中，并评估其在实际应用中的性能和效果。本文的主要目的是设计和实现一个基于耳切法[2]的三维综合集成展示系统三维区域标绘与设备框选系统。本文将详细介绍耳切法的原理和算法，并提出相应的改进和优化方法以适应实际应用场景。通过大量的实验和评估，验证该系统在准确性、效率和用户体验等方面的优势，并与其他相关方法进行比较分析，期望能为三维综合集成展示系统三维区域标绘与设备框选提供一种高效准确的解决方案，促进三维综合集成展示系统领域的进一步发展。

1 三维区域标绘的意义

在三维数字仿真系统中，区域标绘和设备框选是其中最为重要的一部分。通过三维区域标绘，可以以直观的方式清晰地呈现复杂的工厂三维实景，提供直观的信息剖析。通过精确的标绘和设备框选，可以准确地定位设备的位置并提供精确的区域信息，有助于系统的快速定位和监控设备。此外，通过建立三维区域模型，还可以进行区域设备之间的空间关联性分析，有效帮助优化布控和安防策略。

2 技术研究思路

在现有的三维系统中，区域标绘和设备框选主要使用手动标绘、基于深度学习的目标检测和基于点云处理的算法。

手动标绘是通过人工方式在三维场景中绘制区域标记和设备框选。虽然具备灵活性，但占用一定的人力和时间。

基于深度学习的目标检测是利用深度学习技术，如卷积神经网络（CNN）和目标检测算法，自动检测和框选设备。这种方法可以实现自动化和高效性，但对于复杂场景和低质量数据存在一定挑战。

基于点云处理的算法利用点云数据处理和分析技术，如点云分割、点云配准等进行区域标绘和设备框选。这种方法适用于三维点云数据，可以提取特定形状和特征进行标绘和框选。

结合三维综合集成展示系统的实际应用情况和对标绘算法的研究与比较，本文选择了耳切法作为标绘的技术方案。

3 区域标绘

在三维仿真系统中，区域标绘的操作方式一般是用户通过在场景中标绘点，然后系统根据这些点迅速构建出一个多边形或者多边体。通常情况下，用户标绘的点数通常是四个，以构建一个规整的矩形，系统在标绘结束后才会进行绘制。在我们的拓展中，用户可以任意标绘，且当用户标绘的点数达到可以构建一个三角面时，系统就开始进行绘制，并支持增删改的操作。各种多边形，在三维中都是通过用户输入的点构建非镂空的面。构建简单多边形的主要因素是通过点构建三角面，再通过组合三角面形成简单多边形。因此，最关键的是构建三角面，而构建三角面最重要的是对三角面顶点的排序。要实现通过标绘的点实时有序地构建一个非镂空的多边形是一项非常复杂的任务。耳切法恰好是解决三维图形顶点排序的一种算法。[3]

4 耳切法

4.1 简介

在本算法中有一个问题，就是将简单多边形进行转化，变为一组的三角形集合，三角形的所有顶点与原顶点相同。

简单多边形的简介如下：由一组有序点构成顶点，顶点设为P0 至Pn-1。两两顶点间均由边（Pi，Pi-1）依次相连，并且最后一条边（Pn-1，P0）将连接第一个点，每个顶点有且仅有连接两条边，边与边的交点均为顶点，如此组成的一个形状为简单多边形。如图1，图中的三个图形解释了这个概念。可以看出，只有第一个是简单多边形，其他部分只是多边形。我们需要将一个完整的多边形拆分为多个小的三角形，由n 个顶点组成的简单多边形能够根据几何学原理划分为n 减2个三角形[4-6]。耳切法（Ear Clipping）就是用来实现这个目标的算法，其复杂度为O(n^2)。

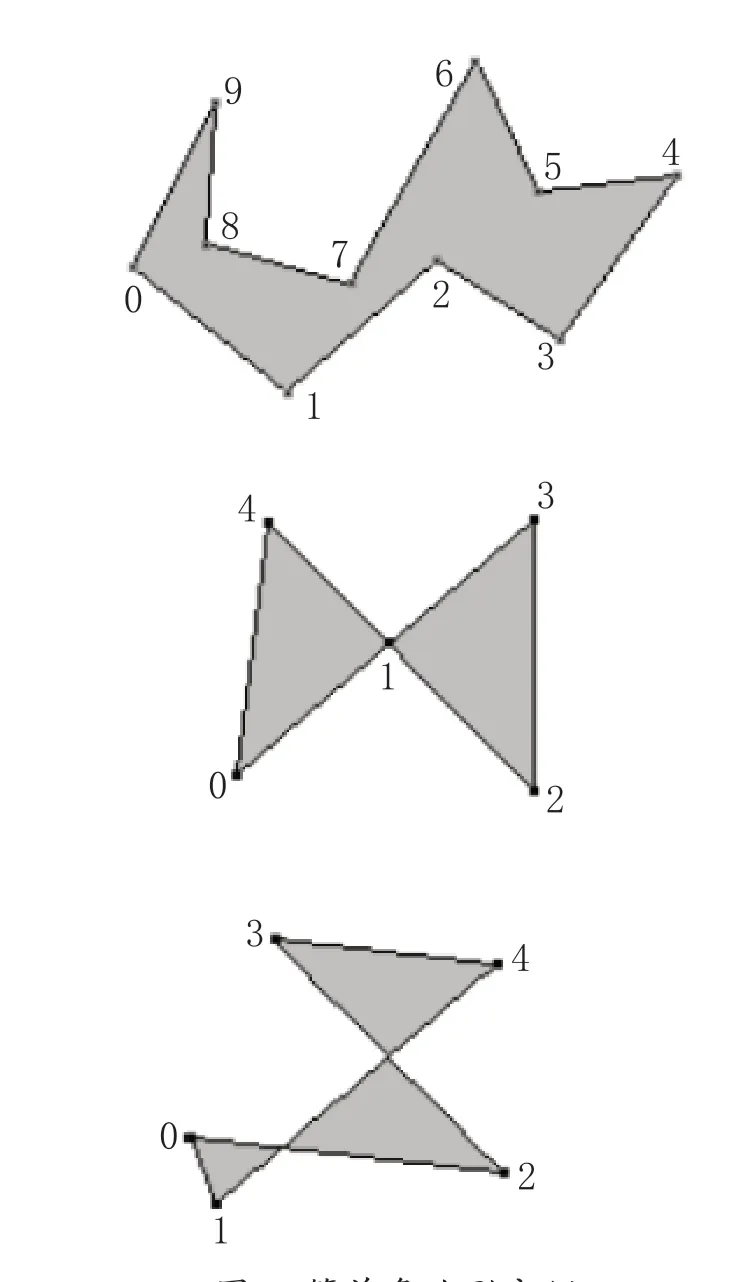
图1 简单多边形实例

4.2 Ear Clipping

简单多边形的“耳朵”是一个特定的三角形。该三角形由多边形中相邻的三个顶点Pn、Pn+1 和Pn+2组成的，并且在该三角形内部不包含其他顶点。Pn 和Pn+2 之间的连线被称为多边形的对角线，其中点Pn+1则被称为耳尖。根据这个特性，我们可以将大的简单多边形拆分为n-2 个小三角形，然后通过查找耳尖并将其所代表的三角形移除来实现拆分过程。

在耳切法的具体实现中，第一步是存储多边形的数据，在此采用的是双向链表[7]结构，双向链表的结构可以减少移除耳朵的时间复杂度，构建链表的所占的复杂度为O(n)。第二步是对所有顶点进行遍历以查找出所有耳朵，需对每个顶点Pi 所在的围绕该顶点的三角形进行检测，判断是否有顶点在三角形内部。如果没有，则Pi 是一个耳朵，否则不是。在实际计算中，需要构建四个链表，其中两个是线性链表，两个是循环链表。其中线性链表用于存储凹顶点和凸顶点。通过计算两边的夹角来确定顶点的类型，夹角大于180 度则为凹顶点，小于180 度则为凸顶点。另外两个循环链表一个用于存储所有顶点的数据，另一个用于存储所有耳尖顶点。

首先计算凹凸顶点，将耳尖与凸顶点相同，然后移除耳尖。如果通过耳尖构建的三角形中存在其他顶点，则将该顶点从耳尖列表中移除。然后对耳尖进行遍历，每次遍历都移除一个耳尖。由于移除一个耳尖后，其相邻的点会发生变化，因此需要判断相邻的点是否发生改变，如果发生改变，则需要更新相关列表。

通过图1 中的简单多边形，我们可以演示耳切法的实现过程和构建。首先通过计算得到两个凹顶点集合R={0,1,3,4,6,9}和C={2,5,7,8}，它们与耳尖相同。然后计算不属于耳尖的顶点，最后得到耳尖集合E={3,4,6,9}。

遍历循环依次移除耳尖顶点。移除耳尖3 后，我们可以观察到耳尖所代表的三角形T1=<2,3,4>被移除，然后对与顶点3相关联的顶点进行判断是否为耳尖，并更新列表，再次移除耳尖。重复这个过程直到耳尖列表为空，最后我们可以看到将图1 中的简单多边形根据耳尖拆分为多个三角形。图2 展示了耳切法移除耳尖的过程：

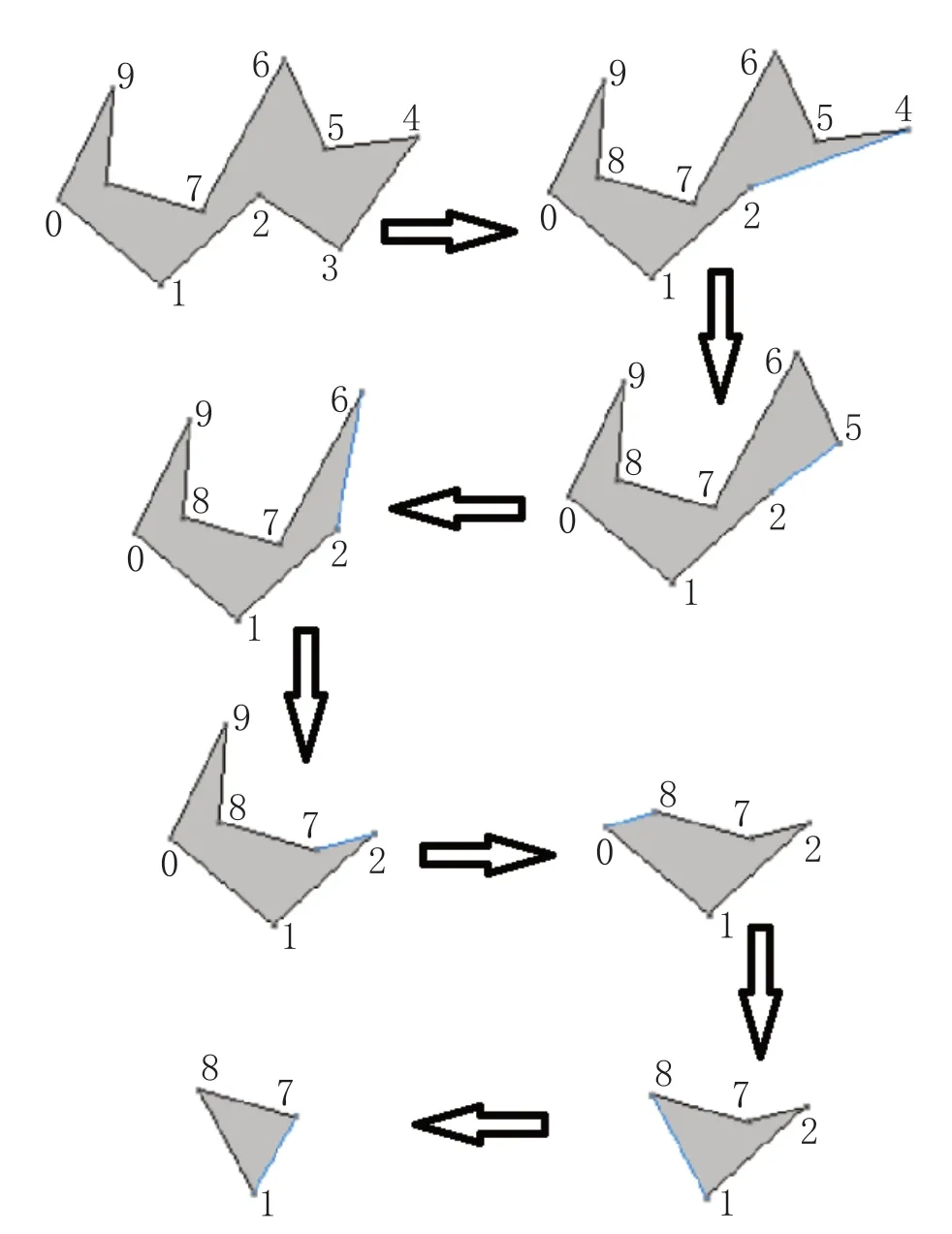
图2 耳切法的实现表现过程

在三维物体的构建过程中，每个需要显示的物体都由多个顶点（点的数量大于等于3）构建基本的三角面，然后通过组合这些面构建整个物体。简单的平面三维物体由四个点构成的两个三角面组合而成。通过耳切法的处理，通过对多个顶点进行计算，我们可以获得多个三角形以及三角形顶点的排列顺序。这样就可以在三维空间中构建一个简单多边形的三维物体。（如图3 所示）

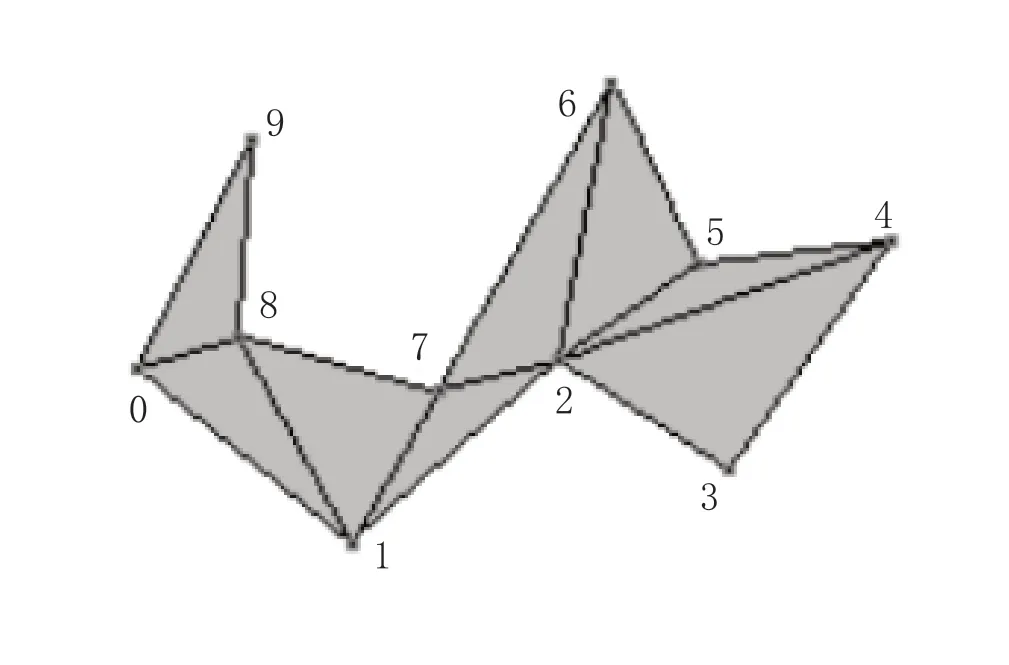
图3 耳切法最终结果

5 耳切法在三维展示系统中的应用

在三维展示系统中，区域标绘是一个不可或缺的组成部分，其主要功能是通过用户点击的点来构建一个立体的区域，并将其以三维形式展示出来。通过应用耳切法对用户标绘的点进行计算，可以快速获得简单多边形的顶点排列顺序，从而能够迅速地绘制用户标绘的区域。这种方法可以实现实时展示和实时编辑修改功能。（如图4 所示）

图4 耳切法在三维展示系统的应用

6 结语

通过本次研究和应用，我们充分利用了耳切法来解决三维展示系统中区域标绘的多边形构建问题，极大地提高了拆分三角形的效率。在区域标绘设备的框选功能中，大大增强了标绘的效率，解决了用户在标绘过程中受限于规定的点数和形状的限制，为用户提供了更好的标绘体验。这种方法大大增强了三维展示系统的丰富性和实用性。

通过以上研究成果，我们为三维展示系统的区域标绘功能提供了一种高效且灵活的解决方案，为用户提供了更好的操作体验。在未来的研究和应用中，我们可以进一步探索耳切法在其他领域的应用，并不断改进和优化算法，以满足不同场景下的需求。