供电系统微电网电源选址定容方法研究

陆晓峰

（国网苏州供电公司，江苏 苏州 215000）

1 前言

随着全球化石资源日渐匮乏和环保问题的突出，风电机组的高效率开发已得到广泛关注，然而其具有的随机、间歇特性会导致电网负荷不稳定，从而引发一系列新的问题[1]。微电网作为一种由分布式电源-储能-负载组成的具有孤岛特性的耦合系统，是保障供电系统安全性与稳定性、新能源高效开发的关键[2]。然而，由于其存储方式与分布方式的差异，会对微电网的运行稳定性、供电品质产生较大的影响，因而需要开展微电网电源的选址定容问题研究。

朱俊澎等人[3]以二阶锥规划为基础，以资金投入周期的经济收益最高为目标，提出一种电源选址定容方法。以闭环配电系统为研究对象，研究包含联络线与分区切换的扩展DistFlow 电力潮流建模方法，并在该方法基础上，构建顾及电力系统动态可重构特性的配电系统最优分配方法。以“有功电流”为基础，采用“虚分支电压”的思想对其进行线性化，并结合电流、电压变量替代及二次锥驰豫，构建一种二次锥型的一体化优化模型。针对含有上界限制条件的二阶锥模型，提出了增加附加电压限制的二阶锥模型。研究成果显示，引入电力系统的动态可扩展性，能够增强电力系统对分布式电源的接纳，增加系统的整体经济性。基于以上研究背景，本文针对供电系统中的微电网电源，提出一种选址定容方法，从而降低选址定容的投资费用。

2 供电系统微电网电源选址定容方法设计

2.1 选取微电网电源的候选地块

为了提高微电网电源选址定容的效率，需要尽可能缩小选址定容的考察面积，但是又不能完全将合适的选址地域忽略[4]，要想提高选址定容的综合效益，本文先选取微电网电源的候选地块，也就是在微电网电源选址定容的过程中，电源所处的地块要比可能被选中的周边地块高，从而选出最优的地块。

在选取微电网电源的候选地块时，往往将电源建设的费用忽略，那么候选地块的总费用Call为：

式（1）中，C0表示候选地块的附加成本，L表示候选地块的地价费用。

如果利用传统的选址定容方法确定微电网电源的位置会导致地价偏高，因此，可以考虑临近的周边地块进行电源选址，但是当微电网电源的位置发生改变时，电源选址的附加建设成本也会随之增加[5]，因此要综合考虑电源选址的地价费用和附加成本建设费用。考虑到供电系统衔接的费用，如果选址定容的成本过高，说明选择的电源位置是不合理的[6]。在供电系统中，多个微电网电源候选地块的衔接必须满足公式（2）的条件，即：

在公式（2）的条件下，给出了选取微电网电源候选地块的具体步骤，如下：

Step1：确定微电网电源选址定容区域的最低地价C′，即：

式（3）中，（rx,ry）表示微电网电源选址定容区域的选址结果。根据微电网电源的建设原理，得到电源候选地块的具体信息，划定微电网电源的选址定容区域，不考虑区域以外部分。

Step2：选择一个地价相对较低的地块，按照Step1将该区域缩小，直到得到目标区域内最低价格的地块。

Step3：将无法继续缩小的候选区域，作为微电网电源选址的区域，邻接区域作为相应的候选地块。

根据候选地块的总费用，给出多个微电网电源候选地块的衔接条件，通过确定微电网电源选址定容区域的最低地价，选取了微电网电源的邻接候选地块。

2.2 设计微电网电源选址定容算法

供电系统中的微电网是由继电保护装置、混合储能系统、分布式电源以及能量转换装置组成的比较独立的发电系统。供电系统在正常运行过程中，微电网电源选址定容问题属于一种非线性的规划问题[7]，将该类问题转化为数学模型的求解问题，那么利用公式（4）给出微电网电源选址定容的数学模型，即：

式（4）中，fn(x)表示数学模型中的第n个子目标函数，y表示微电网电源选址定容的目标函数，g(x)表示目标函数中不等式的约束条件，φ(x)表示目标函数中等式的约束条件，A表示微电网电源在选址定容过程中的决策变量，D表示优化电源选址定容目标的总数，admin和admax表示决策变量搜索的最小值和最大值。

在公式（4）的微电网电源选址定容数学模型下，通过求解微电网电源选址定容问题[8]，设计微电网电源选址定容算法，具体步骤为：

Step1：将微电网电源接入供电系统的容量和位置作为选址定容的决策变量，最小储能容量、电压偏差以及负荷缺电率为优化目标，在功率平衡、节点电压、储能功率及储能平衡等多个限制条件下，构建选址定容模型。

Step2：采用粒子群算法求解step1 中的数学模型，并将相应的求解软件编制到MATLAB 中，将微电网的功率流、节点试验系统的数据、约束条件的上下界和算法的参数等作为初始数据。运行软件程序，计算出每个粒子所对应的目标函数，通过与各个粒子相对应的目标值进行对比，选择出一个最优解和一个群体的全局最优解，并在这两者的基础上，对其进行反复的搜索。

Step3：通过搜索得到的最优解就是最终的配置方案，将其作为微电网电源选址定容的最终结果。

综上所述，将微电网电源选址定容问题转化为数学模型的求解问题，利用粒子群算法，求解了微电网电源选址定容的数学模型，实现微电网电源的选址定容。

3 实例分析

3.1 研究对象

为了验证文中方法在微电网电源选址定容中的经济性，本文以某一地区的220kV 供电系统为研究对象，实验之前，先了解供电系统中电源点和负荷点的地理位置信息，在MATLAB 程序下对其进行优化处理，得到负荷点的地理位置信息，如表1 所示。

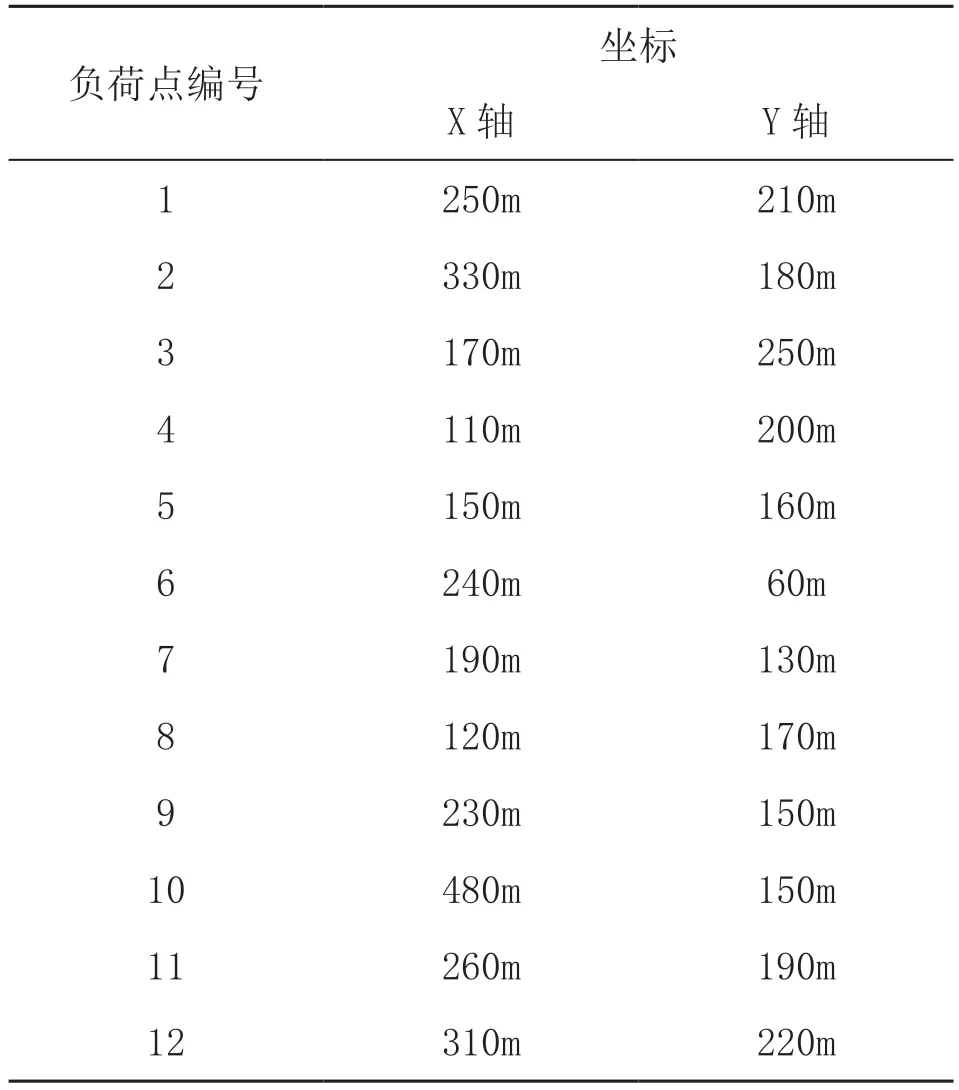
表1 供电系统负荷点的地理信息

将表1 中供电系统负荷点的地理信息导入MATLAB程序中，通过各个负荷点的位置关系，选取微电网电源的候选地块，在该地块内，对供电系统微电网电源进行选址定容，保证供电系统的安全稳定运行。

3.2 选址定容测试

根据表1 中供电系统负荷点的地理信息，利用文中方法对微电网电源进行选址定容，得到如图1 所示的结果。

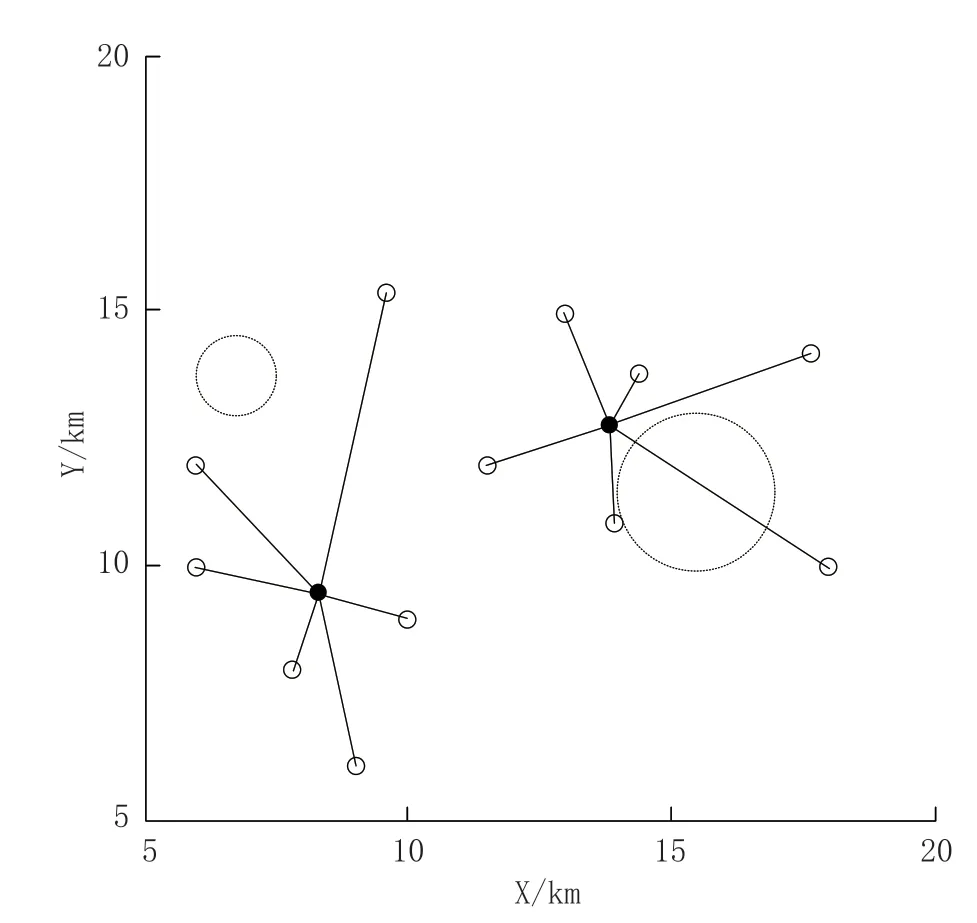
图1 微电网电源选址定容结果

图1 中，黑色实心圆为微电网电源，虚线实心圆为供电系统所处区域的地理信息约束，白色空心圆为负荷点。

根据图1 的结果可知，文中方法对微电网电源的选址定容结果在可建设范围内，可以避免不可建区域，符合微电网电源的建设要求。

3.3 经济性分析

在经济性分析中，本文引入考虑网络动态重构的选址定容方法作对比，统计了两种方法在微电网电源选址定容中的投资费用，结果如表2 所示。

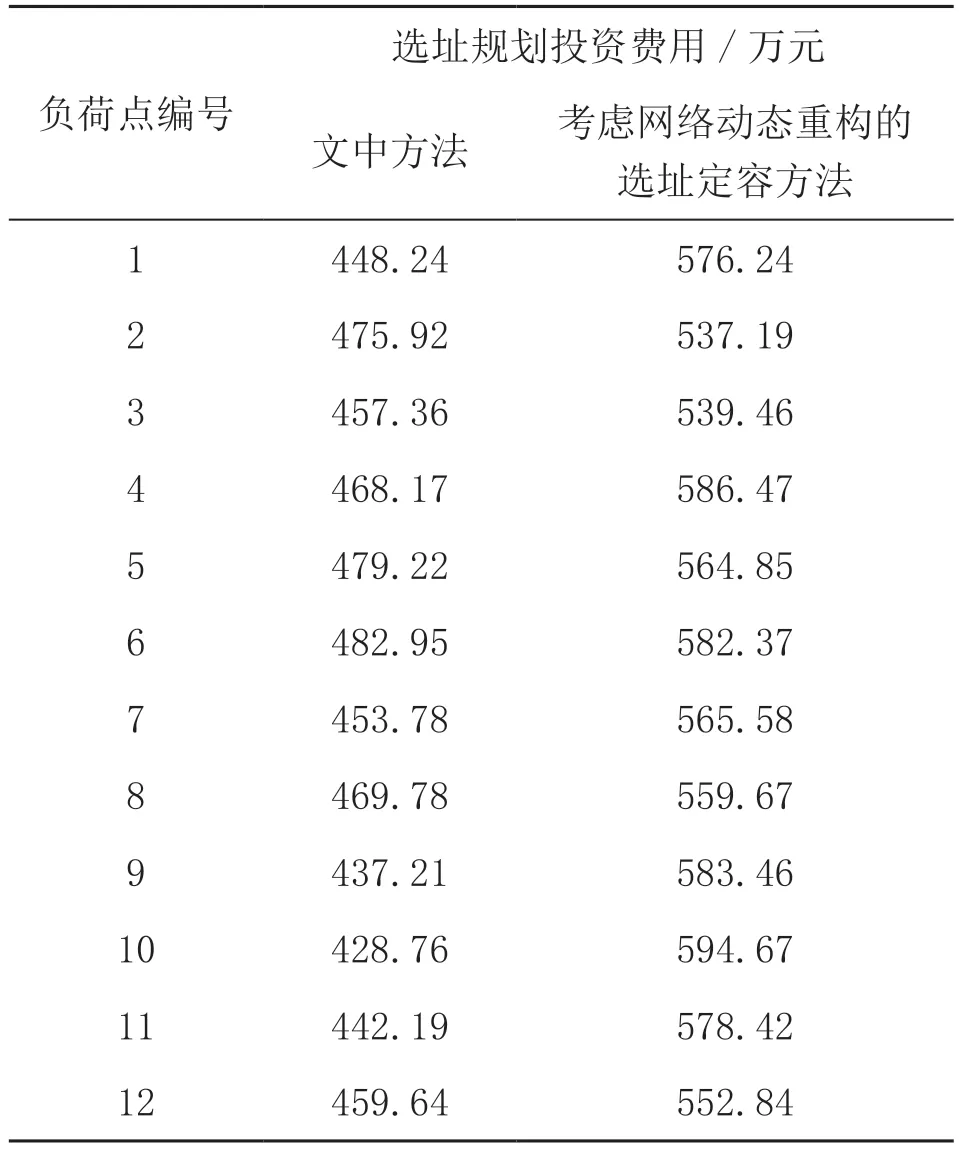
表2 微电网电源选址定容的投资费用

从表2 的结果可以看出，采用考虑网络动态重构的选址定容方法时，微电网电源选址定容的投资费用在500 万元～600 万元之间，文中方法在微电网电源选址定容方面的投资费用比较低，在500 万元以内，说明文中方法不仅可以保证微电网电源选址定容的合理性，还可以降低选址定容的投资费用，保证了微电网电源选址定容的经济性。

4 结语

本文提出了供电系统微电网电源选址定容方法研究，通过选取微电网电源的候选地块，设计了微电网电源选址定容算法，通过实例分析发现，该方法在微电网电源选址定容中比较合理，并提高了微电网电源选址定容的经济性。

本文的研究虽然取得了一定的成果，但是由于粒子群算法在求解时容易陷入局部最优，在今后的研究中，希望可以引入遗传算法优化粒子群算法，得到最佳选址定容方案。