变量选择方法对近红外光谱校正模型优化极限的研究
潘正豪,王 鹏,陈昆燕,李秋潼,唐 杰,杨 俊,邵利民*
(1.中国科学技术大学 化学与材料科学学院,安徽 合肥 230026;2.重庆中烟工业有限责任公司技术中心,重庆 400060)
近红外光谱(Near-infrared spectroscopy,NIRS)是一种介于可见光和中红外之间的吸收光谱,主要包含C-H、N-H和O-H化学键的信息,几乎所有有机物和大部分含氢的分子都可以使用NIRS进行表征。近红外分析方法具有分析速度快、效率高、成本低等特点,被广泛应用于农业[1]、食品[2]、医疗[3]等行业。但是,NIRS 包含很多泛频和合频,这使光谱解析变得复杂,难以在特定波段上找到特定化学键的信息。多变量方法诸如主成分回归(PCR)、偏最小二乘回归(PLSR)、人工神经网络(ANN)等可以用来建立化学校正模型,解析光谱中的有效化学信息。
建立校正模型时,通过变量选择方法使用不同光谱波段数据可以较大程度降低模型的预测误差,提高模型的可解释性和泛化能力[4-6]。变量选择方法可以按照选择策略分为以下几类:基于过滤器的方法如RC[7](Regression coefficients)和RT[8](Randomization test),基于极值搜索的方法如连续投影算法(Successive projections algorithm,SPA),基于顺序搜索的方法[9]如fiPLS(Forward interval PLS)和biPLS(Backward interval PLS),基于详尽搜索的方法如VCPA[10](Variable combination population analysis)和siPLS[11](Synergy interval PLS),基于智能优化的算法如遗传算法[11](Genetic algorithm,GA)和模拟退火算法[12](Simulated annealing,SA),基于模型集群分析的方法如竞争自适应重加权采样[13](Competitive adaptive reweighted sampling,CARS)等。常用的变量选择方法还有蒙特卡洛-无用信息变量消除[14](Monte Carlo-uninformative variable elimination,MC-UVE)、随机跳蛙[15](Interval random frog,iRF)、间隔偏最小二乘法[16](Interval partial least squares,iPLS)等。随着学科交叉的深入和计算机算法的开发,变量选择方法愈来愈多。面对新的数据集,优化其线性回归模型时,经常会遇到两个问题[5,17-18]:(1)若无相关经验,则可能需要逐个尝试常见的算法或开发新的算法;(2)在线性关系较弱的数据集中,有时即使应用变量选择方法,也无法得到较好的回归和预测结果。
笔者在研究烟草样品近红外光谱的PLSR模型时,发现无论应用何种方法,均无法有效提升模型在预测集上的预测误差,这可能说明几乎没有变量选择方法能够在本研究小组的烟草数据集上获得较好的回归效果。理论上虽然可以通过光谱全排列得到最优的变量选择,但是受限于计算速度,实际中无法完成,故优化算法变量选择成为可行的策略[19]。
基于此,本文研究并设计了一种寻找变量选择优化极限的方法,基于蒙特卡洛随机重复试验,生成一系列变量子集,并对这些子集建模和验证,考察子模型在验证集上的预测效果,并记录其预测均方根误差(Root mean square error of prediction,RMSEP),绘制RMSEP 的分布图,从而获得关于数据集和模型的相关信息。
对于特定数据集来说,尝试常见算法与开发新算法或许无法避免,但对于整体优化目标来说,有时需要快速了解一个数据集和模型是否适用变量选择方法,如果适用,该变量选择方法又表现出何种效果。基于该思想,这种通过大量随机试验得到的结果能在一定程度上接近数据集和模型的内在属性,因此可以高效探究变量选择算法对该数据集和模型的适用性:变量选择可以多大程度地优化此模型,变量选择方法在此模型上的优化极限是多少。与其他变量选择方法相比,本方法具有较强的泛化能力,可以获得更低的预测误差。
1 实验及原理
1.1 数据来源
使用3个近红外光谱数据集验证本文提出的方法。
数据集1 来自实验室测量烟草样品的近红外光谱及其果胶含量。样品为重庆中烟和安徽中烟提供的2014~2015 年云南、贵州、湖北、重庆、福建、安徽等产区的烤烟样品共203 个。在Thermo AntarisⅡ型傅里叶变换-近红外光谱仪(Thermo Scientific 热电公司,美国)上按DB53/T 497-2013《烟草及烟草制品主要化学成分指标 近红外校正模型建立与验证导则》[20]规定的方法采集样品光谱,近红外波长范围为1 000~2 500 nm,共获得1 557个变量。按照间羟基联苯法测量样品的果胶质量百分含量。
数据集2、3 来自网络上公开的近红外光谱数据:数据集2 来自https://www. cNIRS. org/content.aspx?page_id=22&club_id=409746&module_id=239453。该数据集由496 个小麦样本组成,近红外波长范围为730~1 100 nm,间隔为0.5 nm(741个变量),包含小麦近红外光谱及其蛋白质含量。数据集3来自https://www. eigenvector. com/data/Corn,选用m5 仪器的光谱数据集,该数据集由80 个玉米样本组成,近红外波长范围为1 100~2 498 nm,间隔为2 nm(700 个变量),包含玉米近红外光谱及其淀粉含量。
3套数据集的基本信息列于表1。
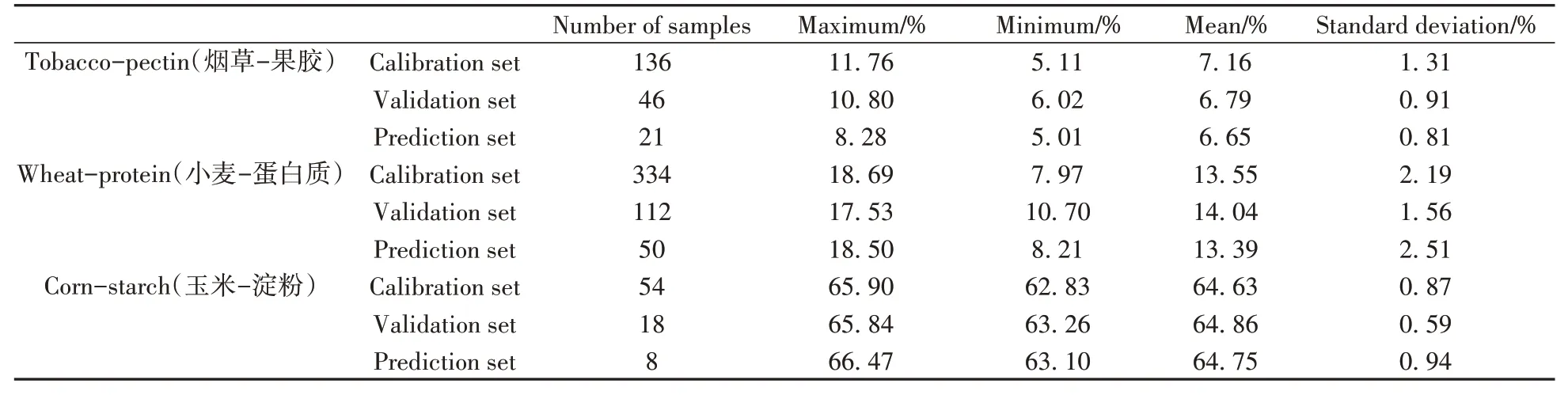
表1 数据集概况Table 1 Basic information on the datasets
1.2 算法步骤
(1)以浓度梯度法在各个浓度区间内选择10%的样品作为预测集;
(2)运用SPXY 方法[21]将剩余数据集划分为建模集和验证集,样本个数比为3∶1。在初始全谱模型上以PLS方法建立回归模型,得到初始模型及其预测误差RMSEP0;
式中,n为样品总数,yi表示样品的真实值,ŷi表示样品的预测值。
(3)设置循环次数echotime和变量选择数s;
(4)在每次循环中,随机选择s个变量点,形成一个变量选择后的新子集;
(5)为每个建模集的变量选择建立PLS回归模型,代入验证集得到评价指标RMSEP;
(6)保留每个RMSEP 值,绘制其分布图,得到可优化率rO和优化极限LO。rO定义为RMSEP 值小于RMSEP0的部分的变量选择数占总循环次数的比值,LO定义为所有循环中出现的最小RMSEP0;
(7)RMSEP 值小于RMSEP0的部分的变量选择是可优化变量选择,统计这些变量选择中每个变量出现的次数,作为每个变量波数的相关性度量;
(8)按照变量波数相关性降序逐个加入最终变量选择子集,在RMSEP值达到最小值时结束。
算法中第2~6步循环过程的流程图如图1所示。
2 结果与讨论
将本研究提出的方法应用于烟草果胶、小麦蛋白质和玉米淀粉3个数据集的处理。首先详细讨论了本方法获取烟草果胶数据集变量选择优化极限的过程;其次,绘制3个数据集的RMSEP 分布图,对比变量选择在不同数据集上的优化效果;最后,比较了其他各种常用变量选择方法在数据集上的表现。
2.1 烟草-果胶数据集变量选择的优化极限
烟草-果胶数据集(数据集1)含有203 个样品,在4 000 cm-1至10 000 cm-1波数上可获得具有1 557 个吸光度的NIR 光谱矩阵X203×1557和果胶百分含量的化学测量值矩阵y。从数据集1中以浓度梯度抽取21个样品(10%)作为预测集备用,采用SPXY方法将剩余数据按照3∶1划分成建模集和验证集,样品个数分别为136 与46。经10 折交叉验证方法得到校正集的主成分数为10,后续子模型的主成分数均取10。
设定循环次数为106次,每次循环中随机选择s=30 个变量随机产生一个变量子集S={v1,v2,v3,…,vs}⊆{1, 2, 3, …,p},S中含有s个变量序号,选择过后的X203×s与y以主成分数A=10 进行建模验证,每次循环得到的以RMSEP 为验证指标的分布图如图2 所示。s的取值为30~50时,能在子模型上取得最佳效果。
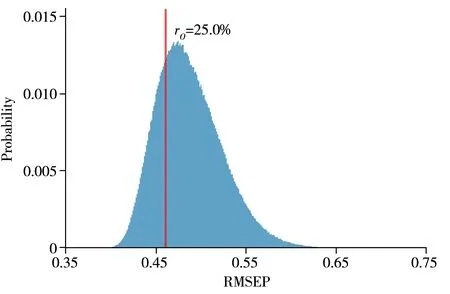
图2 106次循环结果的RMSEP值分布图Fig.2 Distribution of RMSEP after 106 cycles
图2为间距较小的条形频数分布直方图。竖线表示初始模型的RMSEP 值,小于该值的变量选择占比rO约25.0%,是可优化的变量选择比率。从图2 可以看出,变量选择方法在该烟草-果胶数据集中存在优化空间,即任意选择30 个变量,约有25.0%的概率得到比全谱更好的子模型。但同时变量选择方法对其优化也存在上限,任意方法产生的变量选择均不会低于其最小值LO(约0.40)。
以初始模型RMSEP 值作为截断阈值,统计每一个变量被选中的次数,绘制得到如图3所示的频数谱。在所有可优化的变量选择中,每个光谱波数点被选中的频率,表示了这些波数点处的变量在被选中之后对验证集的影响,较好的变量选择被选中,特定波段的频数会高于或低于均值;高频数部分被选中后,更容易组合成较好的变量选择,而低频数部分更不容易。这表明高频数部分(如4 200 cm-1)比低频数部分(如4 800 cm-1)包含较多与烟草-果胶相关的光谱信息。
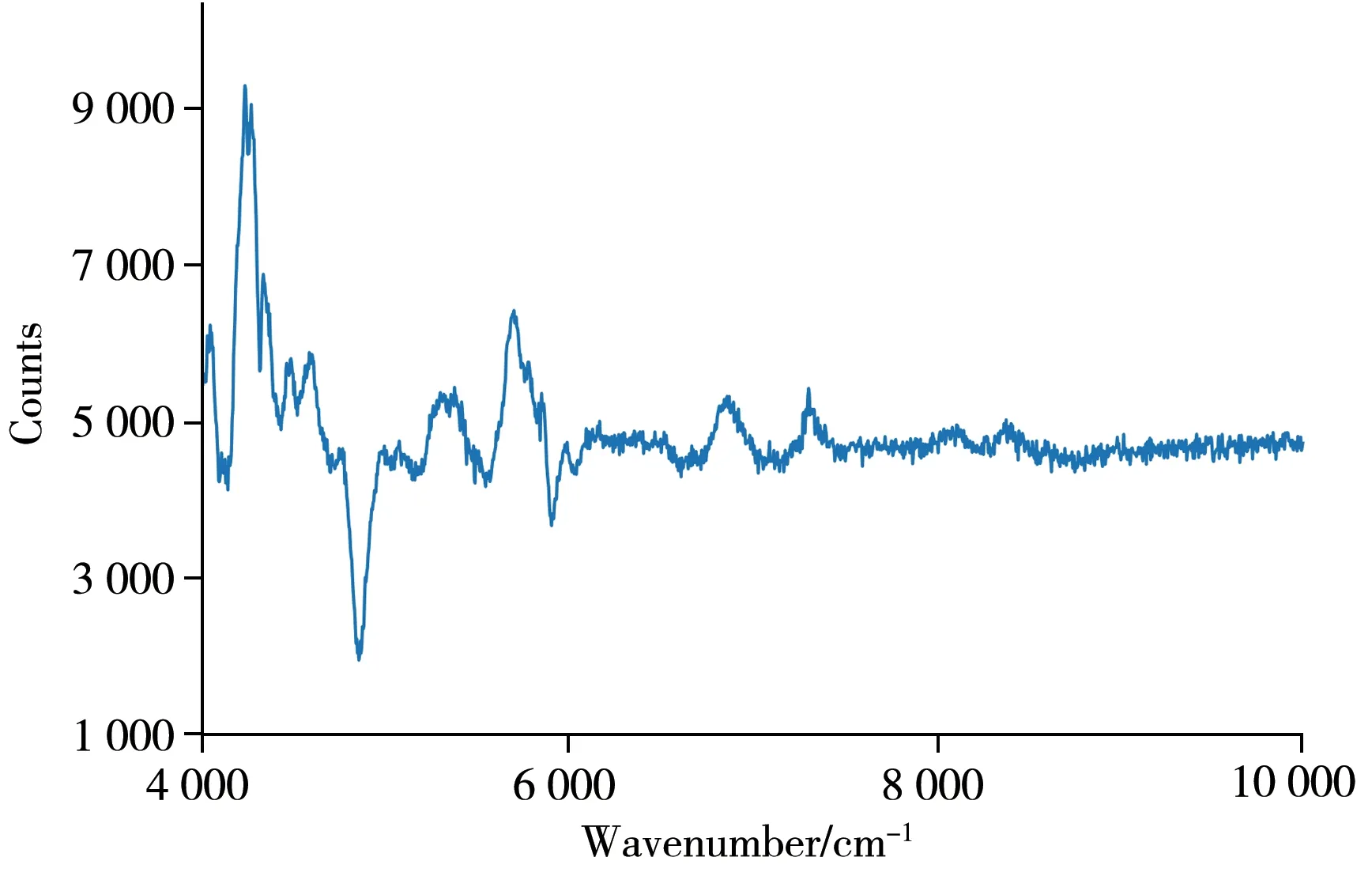
图3 对优化有贡献的波数选择频数Fig.3 Frequency for optimization after variable selection
图3 所示的频数图揭示了NIR 光谱中每一个波数点与待测组分浓度之间的线性校正关系强度。由于蒙特卡洛方法引入的随机噪声,频数谱中存在比较尖锐的锯齿,利用Savitzky-Goaly 滤波将其平滑后按照频数自高至低排列,并逐个加入待选变量集中,每加入一个变量后的子模型均可建模并验证,其RMSEP 值随着加入到变量选择中的变量个数的变化如图4 所示。从图4 可以看出,选择111 个变量后,相应模型的RMSEP 值降至最小值(0.38),算法步骤结束,得到一个含有111个波数的最优变量选择。

图4 RMSEP随加入变量数的变化图Fig.4 RMSEP changes with the number of variables included in model
2.2 变量选择优化效果
对3 个数据集,统一循环次数(106),循环中每次选择30 个变量,子模型使用各自基础模型的主成分数,分别应用本方法研究其PLSR 模型的变量选择优化效果,得到的RMSEP 分布图如图5所示。
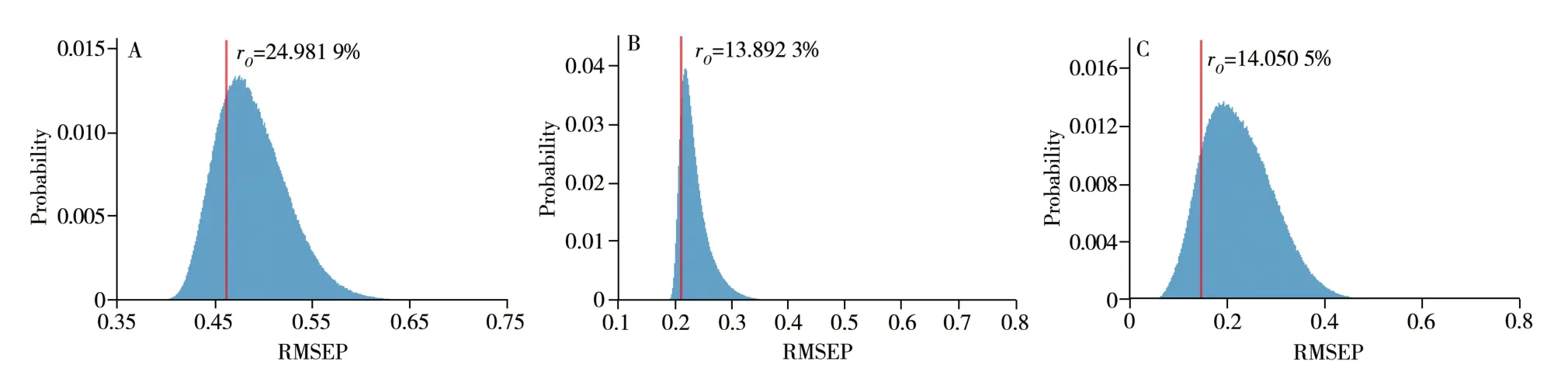
图5 各数据集的RMSEP分布图Fig.5 RMSEP distribution of each dataset
图5A 表明,对于烟草-果胶数据集,变量选择能在一定程度上提升预测的精度,可优化率约25.0%,但提升上限有限(0.40)。图5B 表明,对于小麦-蛋白质数据集,可优化率约13.90%,说明样品之间本就具有较好的线性相关度,全谱PLS 处理之后即可得到较好的效果,能够完成可接受误差范围内的回归预测,变量选择方法几乎完全不能使其预测误差降低,优化极限(0.18)与初始值(0.22)接近,因此变量选择方法不适用于该数据集。图5C 表明,对于玉米-淀粉数据集,可优化率约14.1%,其原始模型的RSMEP 为0.15,提升上限约0.05,这说明变量选择方法在玉米-淀粉数据集上可以有较好的表现,较有可能找到一种变量选择方法使该模型的预测误差降到更低水平。可见,对于不同数据集来说,变量选择方法被应用之后的效果截然不同。
结合表2 可知,玉米中的淀粉含量较高(建模集62.83%),因此相对误差较低,玉米-淀粉模型的相对误差(0.003)远优于烟草-果胶模型(0.063),说明该玉米-淀粉数据集更适合使用线性回归模型,且变量选择方法可以在一定程度上优化模型,提升其预测精度。而烟草-果胶数据集的线性回归模型,使用变量选择方法仅能将预测精度从RMSEP0(0.46)提升至LO(0.39),最多优化约15.2%,若要进一步提升该模型的预测精度,应尝试其他方法或其他模型。
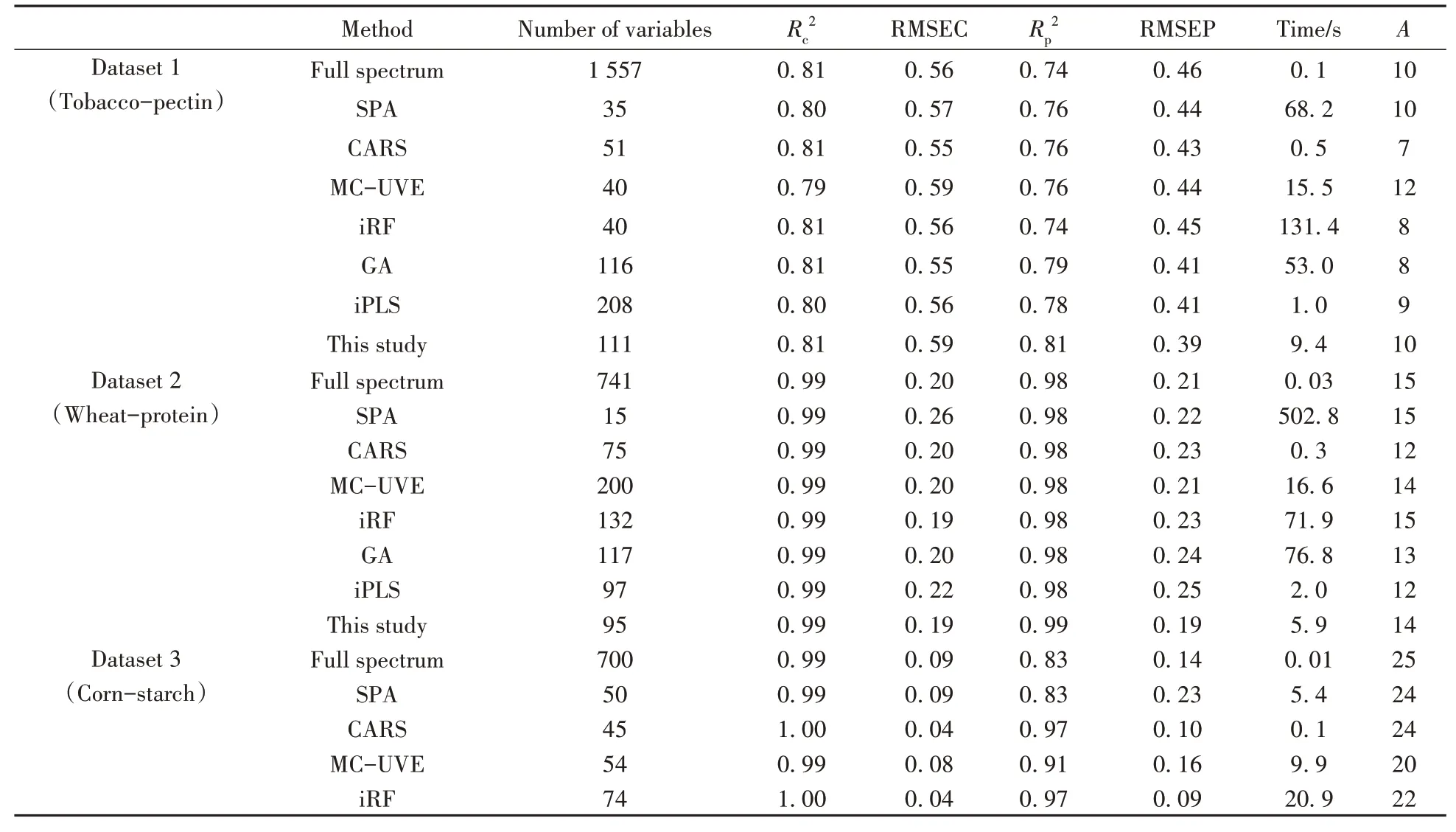
表2 不同变量选择方法下各数据集PLS回归模型参数Table 2 PLS regression model of each dataset under different variable selection methods
2.3 不同变量选择方法对比
对3个数据集应用SPA、CARS、MC-UVE、iRF、GA、iPLS 6种常用变量选择方法进行变量选择并以PLS 建模,与本方法得到的变量选择极限进行对比,其校正集和验证集的决定系数、预测均方根误差列于表2。所有数据均由MATLAB 2021b 运行于搭载AMD Ryzen 5 5600 和Windows 10 操作系统的微机得到。
从表2 可以看出,与不作变量选择相比,大部分变量选择方法均能提高模型预测能力,但提升程度有限。利用本方法对不同数据集探查后发现,变量选择方法对PLS 方法在这些数据集上的预测能力提升效果存在上限。对于数据集1~3,各种变量选择方法的差别较为明显。同一个数据集上,有的方法能够提升模型的回归效果和预测能力,而该方法在另一个数据集上却没有相同的效果。这说明,这些变量选择方法对数据集有不同的适用条件和场景,同时变量选择方法的应用效果也受到数据集来源、品质、特性等的影响。这也就意味着,在利用变量选择方法提升线性回归方法的准确度和预测能力时,如果没有先验经验,无法选择某一特定的方法达到对数据集的优化。
对于不同的数据集,由于实验设计、样品选取等方法的不同,会引入相当大的非线性因素,最终导致近红外数据集在线性回归模型上的效果不能令人满意,如数据集1 中的烟草样品来自全国不同烟草产区,其果胶含量受限于气候、土壤等种植条件而表现出较大的差异性。而数据集2 中的小麦来自同一产地和种植周期,仅仅在麦粒蛋白含量上存在差异,其近红外光谱对蛋白质的线性校正模型具有非常好的拟合度和预测性。
3 结 论
本文提出的基于蒙特卡洛方法的变量选择模式,可以用于检验变量选择算法在各类线性回归模型上的优化极限。较好的回归模型,预测时的相对误差和绝对误差本身就较小,这类模型的可优化率rO和优化极限LO均较小,可以不必采用变量选择方法,直接作为稳健模型进行应用。较差的回归模型,若优化极限LO较小而可优化率rO较大,可以尝试采用变量选择方法得到一些较好的子模型;若优化极限LO较大,则应该放弃使用该线性模型和变量选择方法,转而采用其他方法建模。因此,对于各类数据集及其线性回归模型,采用本方法确定变量选择方法对样品集提升效果的极限是有必要的。
变量选择方法仍存在一些需要解决的问题,如预测模型会对噪声更敏感、妨碍异常值的检测,方法选择存在一定困难等。在面对没有先验经验的样品数据集时,本方法可以在一定程度上提供参考。通过较多次数的随机变量选择,绘制子模型RMSEP 的分布图,一方面可以判断分布曲线最左侧的RMSEP极限极小值,率先了解变量选择方法在模型上的提升上限;另一方面可以根据极小值至初始模型的RMSEP 值截断的分布曲线覆盖面积比、斜率,判断变量选择方法对该数据集的提升效果。最后,在可优化的变量选择中,将不同变量波数被选中的频率,逐一加入变量选择子集中,可以得到一个兼具拟合效果、预测能力、解释性的变量选择。

