面向环境状态监测的振动传感器系统信号辨识

王占生,申晓明,曾轶哲,曾祥豹,谢婷玉

(1. 苏州市轨道交通集团有限公司,江苏 苏州 215008;2. 中电科芯片技术(集团)有限公司,重庆 401332)

0 引言

光纤预警系统以其长距离、高精度、可定制性强等优点逐渐成为管道运输和周界安防保护领域的研究热点。在光纤入侵信号系统中,如何对振动信号进行识别,如何降低光纤预警系统入侵信号的虚警并提高识别率是一个难题[1-5]。为此,国内外研究者提出了各种解决方法,主要有经验模态分解(EMD)、支持向量机(SVM)、极限学习机及卷积神经网络等方法。1998年,Huang等[6]提出了EMD算法,但存在端点效应等问题。2019年,陈勇等[7]采用两次极值波延拓抑制经验模态分解算法的端点效应。 2019年,周子纯等[8]采用SVM和过零率相结合的方法,对攀爬、触碰、撞击、剪切等4种入侵信号进行了识别。2020年,马愈昭等[9]提出基于奇异值分解和改进粒子群优化支持向量机的算法提高分类识别率。 2020年,Jia 等[10]提出一种结合极限学习机(ELM)和fisher准则的评分特征选择的方法,对攀爬、触碰、撞击、剪切等4类事件进行识别。2021年,喻后聃等[11]提出卷积神经网络与Mel倒谱系数相结合,实现了周界入侵识别。 2021年,文献[12-13]提出基于多尺度卷积神经网络的入侵信号特征提取和识别方法,平均准确率达到84.67%。

本文针对振动传感器系统对环境状态中入侵事件识别正确率较低的难题,提出了一种基于随机配置网络(SCN)的神经网络结构用于识别周界入侵的振动传感信号。利用小波降噪对信号进行降噪预处理;再提取信号的能量特征、过均值率、PAR特征;最后采用随机配置网络神经网络对攀爬、触碰、撞击及剪切4种入侵事件进行识别。

1 光纤传感原理

光纤预警系统具有监测距离远,精度高,抗电磁干扰等优点,逐渐成为周界保护领域的研究热点。本文光纤预警系统的主要基本原理是基于光纤应变调制机理。入侵行为会引起相应位置的变形,这将导致光纤传感器相应位置的光纤折射率以及光栅栅格周期发生变化,而折射率将导致光纤中心波长发生变化:

λB=2neffΛ

(1)

式中:λB为光纤的中心波长;neff为光纤纤芯的折射率;Λ为光纤光栅的周期。波长偏移量:

ΔλB=2ΔneffΛ+2neffΔΛ

(2)

式中:Δneff为光纤折射率变化量;ΔΛ为光纤周期变化量。

由式(2)可知,当应力或温度发生变化时,将导致光纤中心波长产生偏移。

2 基于光纤传感器的入侵系统结构

图1为基于光纤传感器的入侵识别系统。首先通过光纤数据采集系统采集振动信号,再将信号上传至电脑;然后利用小波对信号进行降噪处理;对处理后的信号提取其时频域特征并建立数据集,最后通过随机配置网络对其分类。

图1 基于光纤传感器的入侵识别系统图

3 数据预处理

3.1 小波去噪原理和方法

原始信号中常有含噪声数据,含噪数据可表示为

f(t)=s(t)+n(t)

(3)

式中:f(t)为含有噪声的观测数据;s(t)为真实信号;n(t)为噪声信号。

含噪信号经小波分解后,可得到一系列的小波系数,在变换域内有用信号的能量主要集中在幅值较大的系数上,而噪声信号的能量呈均匀分布,因此可选取合适的阈值将噪声信号进行剔除,从而达到去噪的目的。图2为基于小波阈值的去噪原理图。

图2 基于小波阈值的去噪原理图

3.2 阈值函数和阈值选取

采用小波阈值方法去噪时,阈值函数与阈值的选取很重要,对信号去噪起关键作用。硬阈值函数只是简单地保留或去除信号,且设定阈值λ处不连续,可能会使重构的信号产生伪吉布斯现象。软阈值函数则避免了该问题,将绝对值大于λ的小波系数减去固定阈值,从而使该函数在λ处连续,使输出的信号更平滑。

由于变形监测点的形变在时空上是连续的,因此,本文选取软阈值函数作为去噪函数。硬阈值函数为

(4)

软阈值函数[2]为

(5)

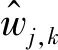
(6)

式中:δ=median(|wj,k|)/0.674 5为噪声标准方差;M为信号长度。

3.3 小波去噪精度指标

选择不同的小波函数与分解层数,其去噪效果有所不同。去噪效果主要通过均方根误差(RMSE)和信噪比(SNR)来衡量,均方根误差越小、SNR越高,去噪效果越好。定义均方根误差为

(7)

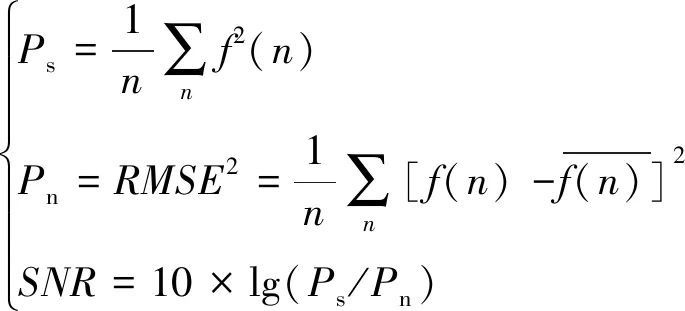
(8)

式中:Ps为真实数据的功率;Pn为噪声的功率。

4 特征提取

4.1 过均值率

由于光纤中心波长受环境的影响,有无入侵信号时中心波长的偏移量不同,而在不同入侵信号之间,过均值率也不同。本文采用过均值率来判断是否有入侵信号,过均值率为

(9)

式中:N为采样点个数;ymean为均值;yzero为幅值与均值的差值;z为过零率。

4.2 能量特征提取

短时能量特征可反映信号波动强度随时间变化的瞬态变化,在周界安防中通常作为振动信号的一种特征。设信号f(t)的快速傅里叶变换(FFT)为F(w),根据快速傅里叶变换(FFT)规则及巴塞伐(Parseval)恒等式有:

(10)

式中:f(t)为时域信号;F(w)为经过傅里叶变换的频域信号;P(w)为FFT功率谱;E为能量信号。

4.3 峰均比

峰均比(PAR)特征是指能量最大信号幅值与均值之比。不同的入侵信号存在幅值和均值上的不同,故可用该特征作为分类的依据。

5 随机配置网络(SCN)

图3为SCN神经网络结构图。SCN神经网络是由区间随机向量函数链路网络(IRVFLN)演变而来。由于其受隐藏层节点的权重及偏置的影响,无法保证其逼近能力,因此, SCN通过引入约束条件提高网络的收敛能力。

图3 SCN网络结构图

IRVFLN神经网络的L-1个隐藏层节点的输出可以表示为

(L=1,2,…,Lmax)

(11)

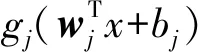
当前预测值fL与真实值f的误差eL可表示为

eL-1=f-fL-1

(12)

通过式(11)、(12)推导可得:

(13)

为确保神经网络可以收敛,对SCN神经网络在IRVFLN神经网络的基础上提出了约束条件:

(14)

式中:0

6 模型实现

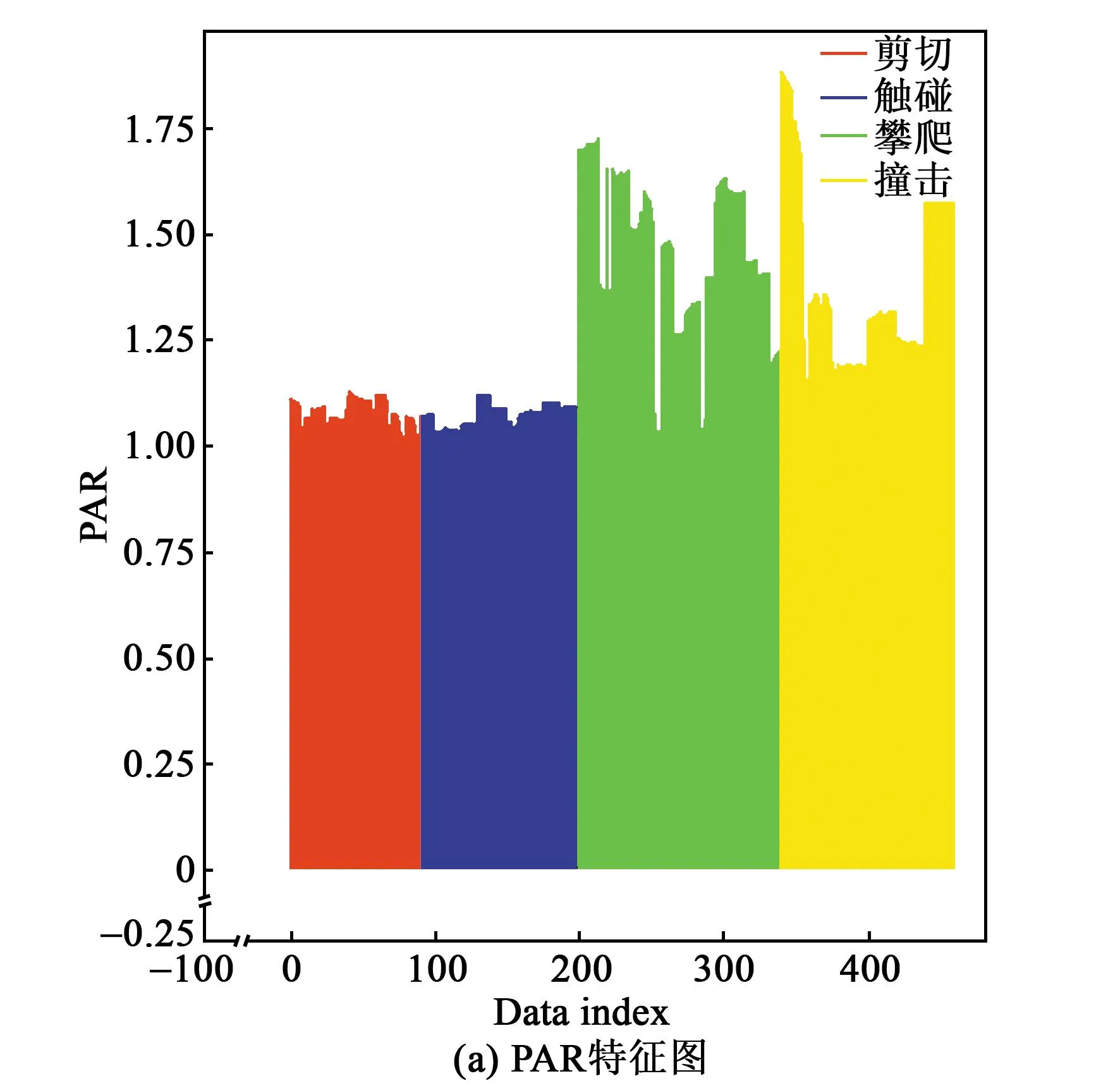
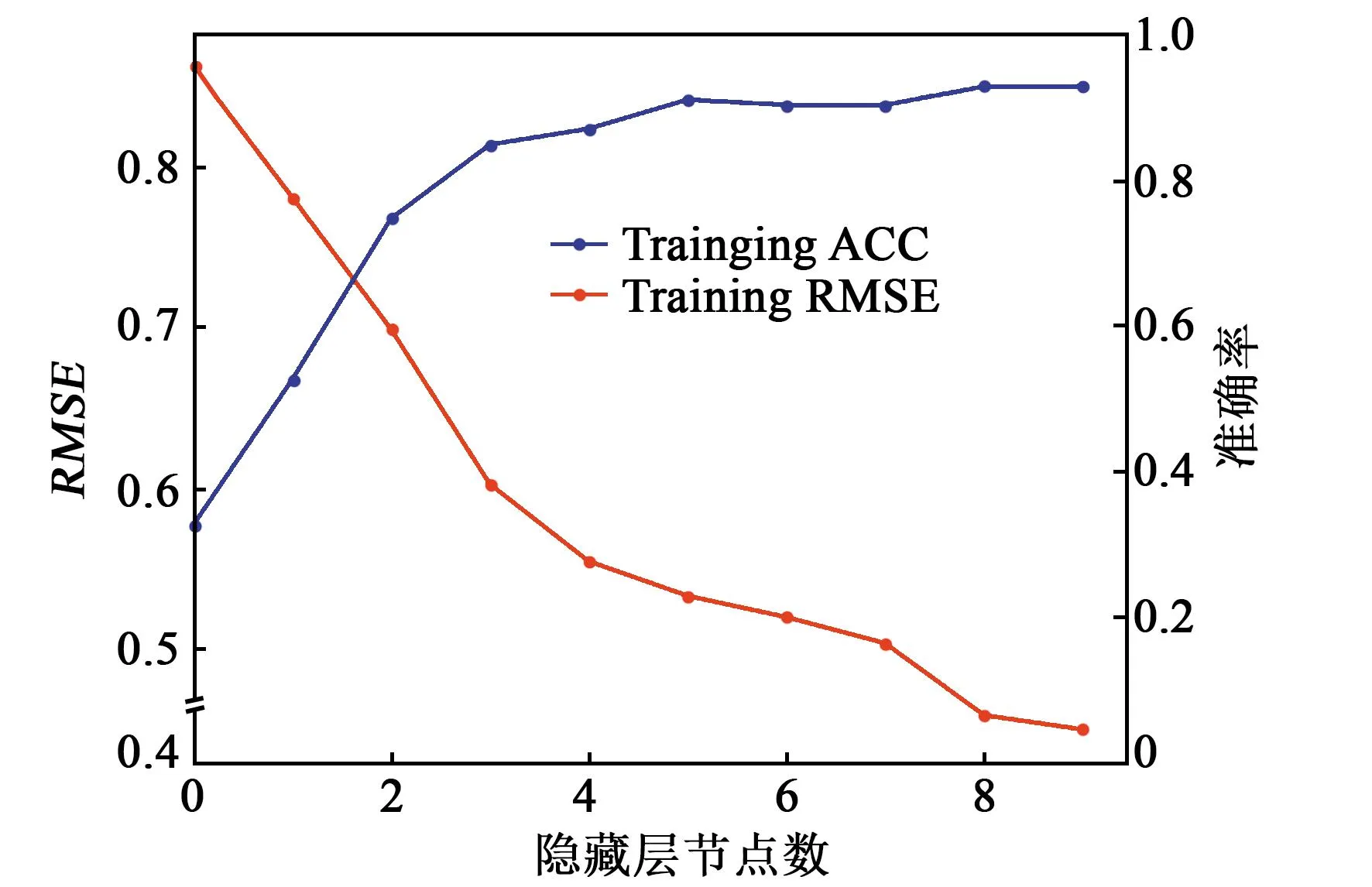
6.1 平台搭建

实验平台如图4所示。在周界入侵实验中,本文使用的光纤解调仪型号为FI-104,采样频率为2 000 Hz,共有4个解调通道,每个通道最多可解调30个光纤信号。将光纤传感器利用粘合剂固定到围栏上,可对攀爬、触碰、撞击、剪切4 种信号进行识别。

图4 周界入侵信号采集平台

6.2 信号采集

光纤解调仪的采样频率为2 000 Hz,即1 min采集120 000个点,部分采样点信息如图5所示。由图可看出,不同的入侵信号在时域上差异较大。

图5 4种入侵信号

6.3 信号预处理

在获得原始信号后,本文采用小波对其进行降噪处理。图6为对攀爬信号进行降噪处理前后的对比。通过小波降噪后,攀爬信号在局部细节上更平滑。

图6 小波降噪对比图

6.4 特征信号提取

提取信号的PAR特征、FFT能量特征及过均值率,图7为信号特征图。由图可看出,每种入侵信号在各个特征上的幅值不同。

图7 信号特征图

6.5 利用SCN实现分类

通过SCN训练,设置隐藏层最大节点数(Lmax)为10,最大误差为0.01,r= [0.9,0.99,0.999,0.999 9,0.999 9],每次最多可添加1个节点。最后训练得出节点数L=10,权重W为(4,10)的矩阵,偏置b为(1,10)。

如图8所示,训练过程中随着隐藏层节点的增加,训练集的准确度达到92.75%。其均方根误差在训练过程中逐渐减小。图9为在测试集上的预测结果,最终预测的准确率为90.7%。由图9可看出,SCN可实现4种入侵信号的分类,但在剪切、攀爬、撞击上的准确度还有待提升。

图8 训练准确度和误差

图9 训练集及测试集结果

图9(a)、(b)为训练过程中测试集和训练集训练的结果。由图9可看出,在敲打、攀爬、触碰、剪切入侵事件中,都有较高的准确率。测试集上剪切、触碰、攀爬、敲打识别准确率分别为82.7%、100%、94.4%、91.6%。

7 结束语

本文利用随机配置神经网络能够自动快速构建万能逼近器的特性,提出了一种基于随机配置网络的周界入侵系统信号识别方案。首先通过光纤采集系统对剪切、攀爬、触碰、敲打4种周界入侵信号进行采集,共采集460组入侵信号,并将其40%作为训练数据集,60%作为测试数据集。考虑存在环境噪声的问题,本文通过小波对原始信号进行降噪,然后提取信号的PAR特征、过均值率及FFT能量特征,最后采用SCN神经网络对4类入侵信号进行分类。训练集的分类准确度可达92.75%,在测试集上准确率为90.7%。这表明所提方法能有效识别周界入侵信号。