压电陶瓷定位平台的复合控制系统研究

姜佩岑,刘曰涛,于长松,温尚林,王福凯

(山东理工大学 机械工程学院,山东 淄博 255049)

0 引言

近年来,随着科学技术的迅速发展,各行各业对高精度定位有更高要求[1]。如在物理学、光通信、生物检测、微电子、航空航天等领域中,对精度的要求达到了微纳米级。因此,一个理想的精密定位平台是保证实现高定位分辨率的关键[2-3]。压电陶瓷凭着分辨率高,无磨损,效率高,强度大,响应速度快及不发热等优点成为了一个理想的执行机构[4]。压电陶瓷的驱动原理是利用逆压电效应,使其迅速完成电能和机械能间的转化,且其响应速度迅速[5-6]。但压电陶瓷固有的迟滞性和蠕变性影响其精度,其中迟滞性问题占主要地位,所产生的非线性误差可达最大量程的10%～14%,导致压电陶瓷定位平台的执行机构在运动过程中不能准确定位到目标位置,甚至可能导致工作系统震荡,不能满足对精度的要求[7]。

为了提高压电陶瓷平台的定位精度,一个理想的复合控制系统起着重要作用。理想的控制系统可以降低压电陶瓷自身特性带来的不足,从而满足对压电陶瓷定位平台的精度要求。本文采用复合控制方法,提出一种基于分段式的Prandtl-Ishlinskii(P-I)模型前馈补偿的复合控制系统,引入比例-积分控制器作为负反馈,在保证响应速度的情况下,负反馈部分采用数字电路,使其具有更高的抗干扰能力,具有一定的学术意义和较高的工程实用价值。

1 压电陶瓷定位平台迟滞模型建立

针对压电陶瓷迟滞特性建立静态迟滞模型。目前迟滞模型可分为物理学模型和现象学模型两大类。本文选用现象学模型中Prandtl-Ishlinskii模型,是一种在Preisach算子的基础上优化得到的模型。该模型从压电陶瓷迟滞性的特征入手,更好地拟合压电陶瓷定位平台的迟滞特性。该模型的Play算子如图1所示。

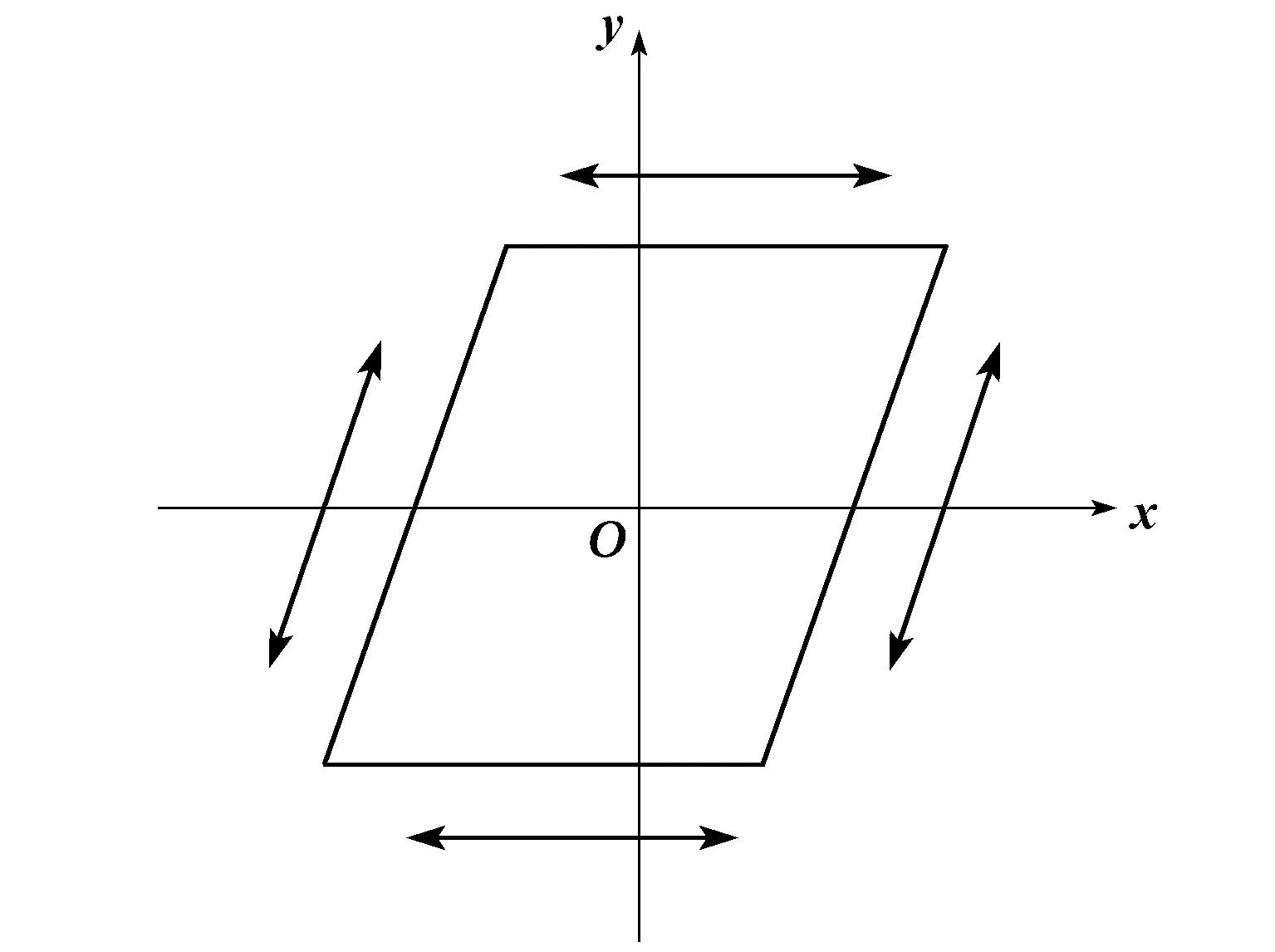
图1 单个Play算子

与Preisach模型相比,P-I模型的双重积分计算过程少,降低了计算难度,不仅有利于控制系统的实现,还提高了响应速度。P-I模型是各个阈值对应的Play算子加权积分后得到的压电陶瓷定位平台的电压和位移的关系构成的。由图1可看出,单个Play算子是奇对称结构,因此P-I模型是一种奇对称模型。单个Play算子:

fr(v(t),w(t))=max{v(t)-r,min(v(t)+

r,w(t)}

(1)

式中:r为Play算子的阈值;v(t)为控制系统在t时刻时给定的输入;w(t)为Play算子在t时刻的输出,其初始值为

w(0)=Hr[v](0)=fr(v(0),0)=

max{v(0),min(v,0)}

(2)

有限个数不同阈值的Play算子加权积分后得到P-I模型。不同阈值的算子描述不同的迟滞特性现象的输入、输出间的关系。因此,由P-I模型描述的压电陶瓷迟滞特性更精确。加权叠加后Play算子的表达式为

Fk(v(t),w(t))=samax {v(t)-

r,min (v(t)-r,w(t)}

(3)

式中:Fk为阈值r的加权Play算子在t时刻的输出;sa为Play算子的权值。

再对各个阈值对应的Play算子进行加权积分,得到P-I迟滞模型的表达式为

r,w(t)}

(4)

式中:y(t)为P-I模型在t时刻的输出;k为算子的个数。

P-I模型的拟合精度与Play算子的个数有关,算子个数越少,拟合精度越低;算子个数多,虽可提高拟合精度,但也增加了计算复杂性。所以在保证精度的前提下,算子个数越少越好。算子个数与位移误差如图2所示。

为了得到最合理情况下算子的个数,在3～17个算子中进行比较。经过比较发现,当算子个数为11时,位移的平均误差为0.22 μm;算子个数继续增加,位移误差无明显减少,可实现在保证建模精度要求下,降低算法的复杂程度。

2 迟滞逆模型参数辨识与验证

选用的P-I迟滞模型存在逆解,同时其逆模型也是一种奇对称的P-I模型。压电陶瓷的迟滞性是不对称的结构,对压电定位平台施加电压,并测得电压与位移的关系,得到迟滞曲线图如图3所示。

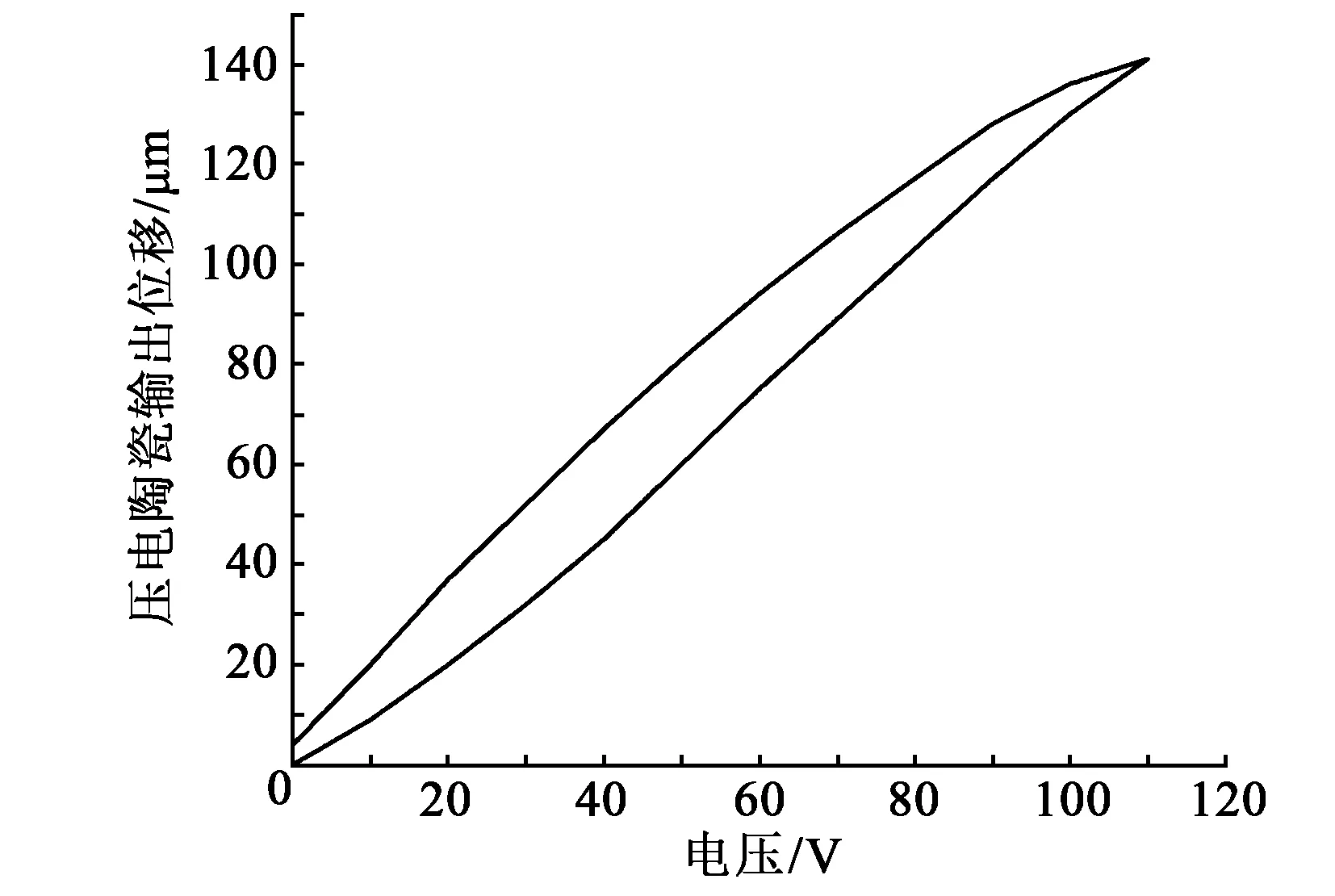
图3 压电陶瓷的迟滞曲线

对此提出分段式的P-I模型进行拟合,对升程和回程进行分别建模,权值的选择通过对加速度矢量(dv/dt)的大小进行判断,以确定升压段或降压段。逆模型的解与P-I模型的乘积是一个单位矩阵(yy′=E),对于不同段,逆模型的基础数学表达式均可表示为

r′,w′(t))}=s′rF′r[y,y′]

(5)

其中:

(6)

(7)

利用Matlab在同一段三角波下进行仿真,将传统P-I模型、分段式P-I模型与实际测量值进行对比分析,结果如图4所示。分段式P-I模型的误差优于传统P-I模型,平均误差从3.7%降低到0.69%。

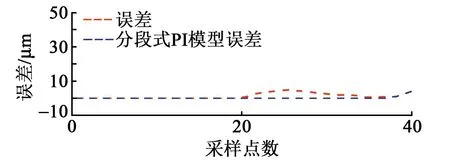
图4 传统PI模型与分段式PI模型误差对比

3 压电陶瓷定位平台控制系统设计

设计一种基于前馈补偿的复合控制系统,在基于分段式P-I迟滞逆模型的前馈逆补偿的基础上引入反馈,在保证响应速度的前提下,负反馈部分采用数字电路,使其具有更高的抗干扰能力。

3.1 前馈控制设计

前馈控制是一种开环控制,响应速度快,利用建立的模型充当导向作用[8-9],因此这类控制的精度取决于建立模型的精度。对于压电陶瓷执行器,前馈控制也是最便捷的抵消迟滞性影响的方法,是一种直接控制的方法[10]。如图5所示,开环前馈控制是将输入的期望位移转化为控制的输入电压信号,进而控制压电平台的执行器,响应速度快,且能较大的纠正迟滞性带来的误差,但不能对误差进行改进。

图5 前馈控制结构图

3.2 反馈控制设计

虽然有前馈补偿起导向作用,理论上能达到较高的精度,但实际应用中,任何环节一点微小的误差都会影响压电陶瓷定位平台的实际位移输出,因此引入负反馈,对实际应用中产生的误差进行补偿,可提高平台的控制精度。

为了使系统具备良好的稳定性,产生较小的噪音及拥有更高的控制精度,在前馈补偿的前提下引入反馈,设计一种串联PI控制电路。其中反馈控制器分为比例环节和积分环节,二者相互独立,提高了系统的稳定性和响应速度。PI控制器的控制规律表示为

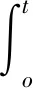
(8)

式中:U(t)为控制输出电压;e(t)为输入位移v(t)和输出位移w(t)之间的差值;Kp、Ki分别为比例、积分系数。

反馈控制器采用二进制数字信号的数字电路,无噪音积累,抗干扰能力强,更有利于远距离存储和运输。因此,加入数字电路使系统更稳定可靠,从而减少了不必要的误差。

采用双极板式电容传感器对压电陶瓷定位平台的位移进行检测。与应变片式电容传感器相比,电容式传感器结构简单,安装方便。对于高精度的设施,复杂的安装工序会增加误差值。因此,采用电容式传感器在保证分辨率的前提下可增强系统的抗干扰能力。

对反馈回路进行设计优化,正弦激励电路原理图如图6所示。选择有源石英晶振电路作为激励信号的信号源,使其产生稳定幅值和频率的正弦激励信号,该信号可将待测电容值转化为电压值。激励信号的质量是决定检测电路是否有效的关键。信号首先经过A1输入运算放大器LF353-N和电阻R2、R3,以及双T性陷波滤波器组成的选频放大电路,然后通过由A2运算放大器AD818及对应电阻和场效应管构成稳压调节电路,输出具有稳定幅值和频率的激励信号,该正弦激励电路的传递函数为

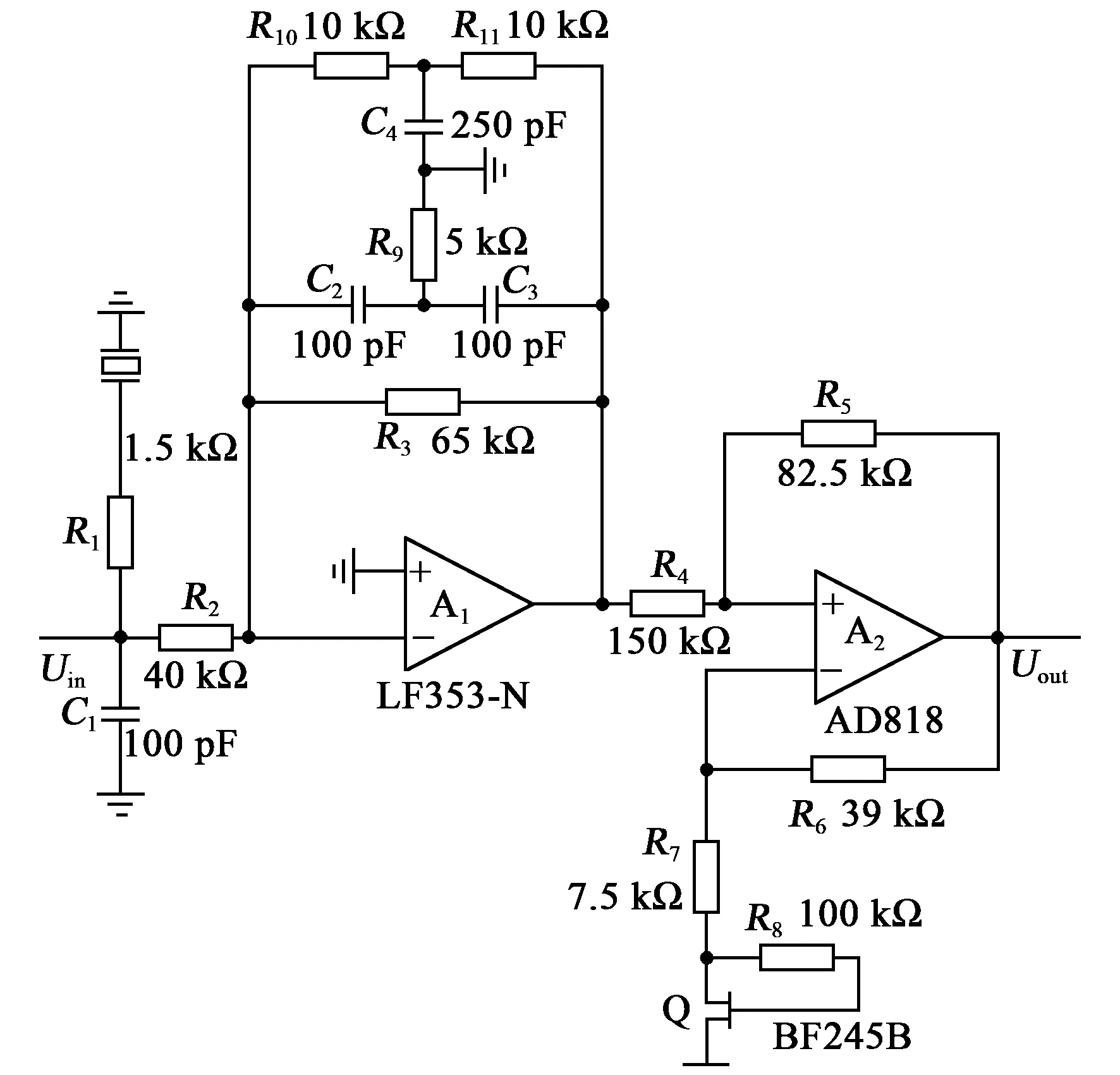
图6 正弦激励电路

(9)

电容转换电路选用双极板式电容传感器,利用检测电路对电容传感器的电容变化进行调制,然后输出电压值,原理图如图7所示。电容的变化量很小,需要增大放大器增益及输入阻抗,确保提高反馈回路的灵敏度。因此,由A1运算放大器(OPA637)、电阻R1及电容Cr、C1构成高通滤波器。通过电阻和电容值的改变控制双T型滤波器的频率。A2运算放大器(AD818)和双T型滤波器构成陷波滤波器。该转换电路的传递函数为

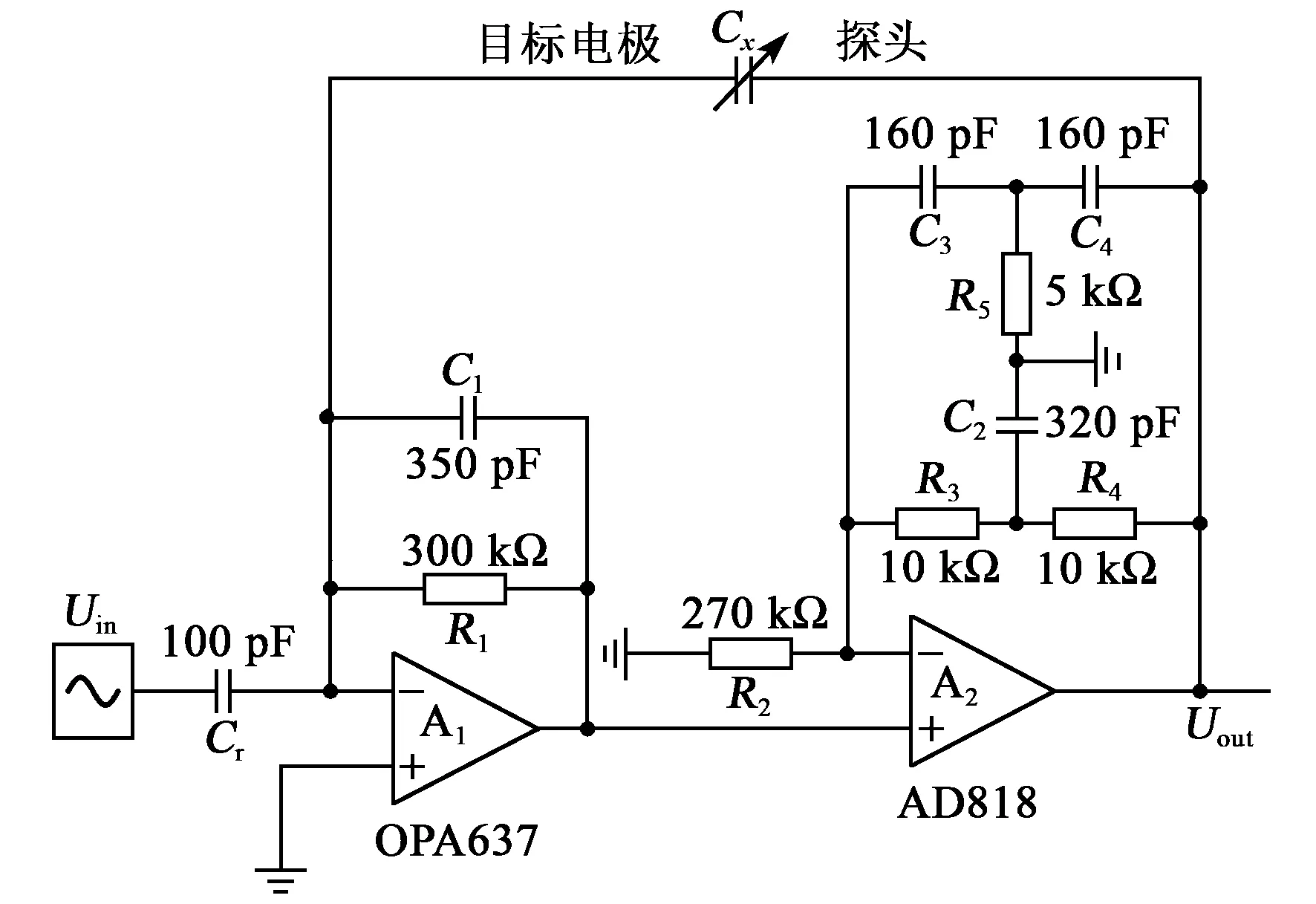
图7 电容转换电路

(10)

式中:Uin为输入电压;Uout为输出电压;Cr为已知参考电容;Cx为待测电容。

3.3 复合控制系统设计

为进一步提高系统的定位精度,在前馈逆补偿的基础上引入反馈,本文提出一种基于前馈补偿的复合控制系统,如图8所示。前馈基于分段式的P-I迟滞逆模型,反馈控制器采用串联式PI控制器,可保证有较高的响应速度,同时也有较高的精度,且更适合应用于实际工程中。

图8 复合控制结构图

在前馈作为导向的前提下,反馈回路具有微调的作用,有利于在最短时间内尽可能减少误差,提高系统的定位精度。因为压电陶瓷的迟滞特性,PI控制器内比例、积分部分在电容传感器检测到误差信号时,检测电路输出包含位移变化的直流电压分量,经A/D转换电路实现数字化处理,保证误差信号传输时的可靠性和稳定性,有利于信号的存储和传输。比例部分对误差信号进行迅速放大,放大后误差信号由积分部分进行积分,经D/A转换电路输出驱动电压信号,控制压电陶瓷产生伸缩变形。

4 实验与结果分析

该实验平台用STM32F103VET6搭建控制器,用Visual C++作为编程语言,反馈电路由正弦激励电路和电容转换电路构成,压电平台由压电陶瓷和柔性铰链构成,其余部分由驱动器、TDS1012B-SC数字储存示波器、IT6722可编程直流电源等组成。通过上机位输入一个期望控制信号,前馈逆模型输出补偿后的数字电压信号,控制器内部的D/A转换电路输出相应的模拟信号,驱动电路控制压电陶瓷定位平台的执行器产生相应的位移,然后通过电容传感器检测出位移差,经检测电路后输出包含位移变化量的电压信号,经A/D转换电路后输出数字信号并反馈到反馈控制器内。实验测试平台如图9所示。

图9 测试平台搭建

在测试行程为0～140 μm时,对压电陶瓷定位平台从反向极限到正向极限进行输出。起始点在反向极限处,进行5个周期循环,每个周期设置11个采集点,分别为pi(i=1,2,3,…,11),第i个测量位置准确度Ai可表示为

(11)

式中:Pij为第i个位置的第j次测量值;Pi为第i个位置的理论值;n为测量次数。

取A=max (Ai),作为平台测试的准确度,再分别对5个周期中压电平台的输出位移进行记录,得出在复合控制系统下压电定位平台的性能实验结果,如图10所示。

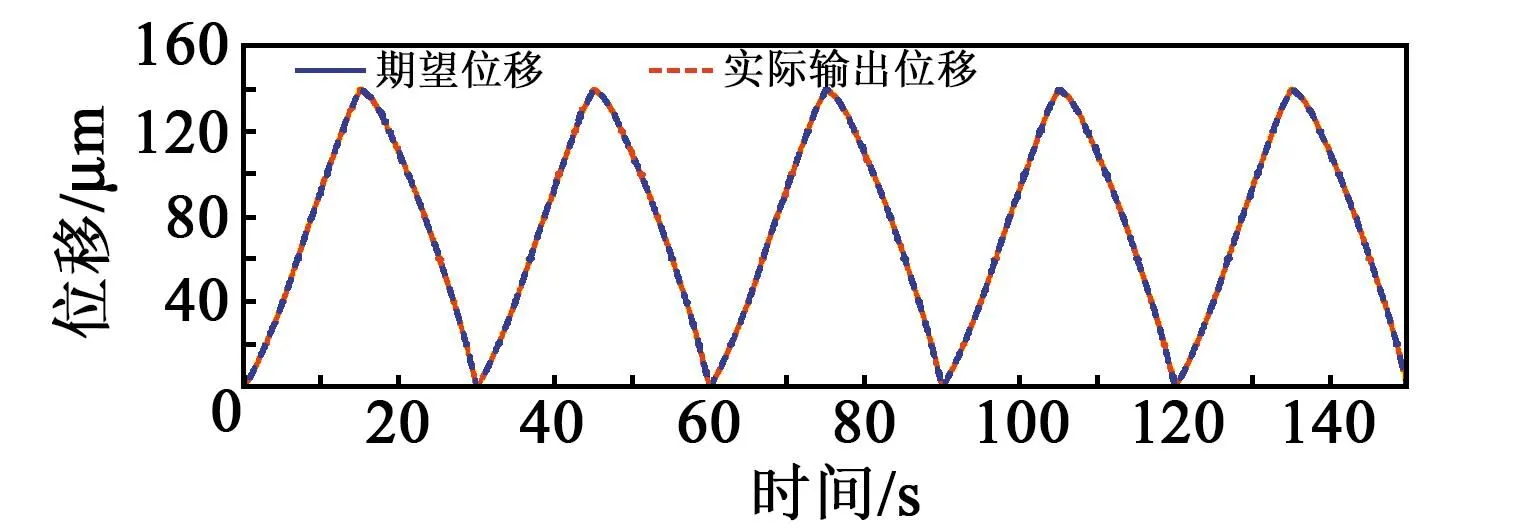
图10 期望位移与实际输出位移对比曲线

由图10可看出,压电陶瓷定位平台的实际输出位移与期望位移误差较小,且未出现与期望位移偏移的情况。比较两种位移行程,得到的误差如图11所示。由图可看出,实际位移所产生的误差较小,且存在一定的周期性规律,最大误差出现在升程段与回程段交汇处,以及回程段的回零点处。

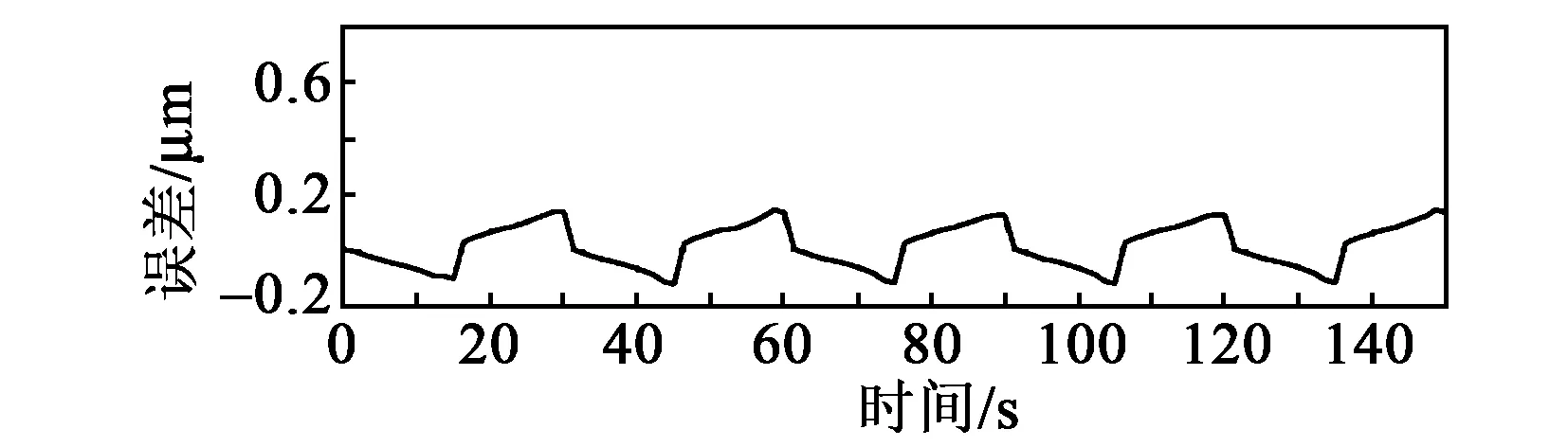
图11 期望位移与实际位移输出位移误差

在复合控制系统和仅有开环控制的情况下,对两种控制精度进行对比分析,并记录在1个周期下的误差对比,如图12所示。由图可看出,复合型控制系统的控制精度更高。

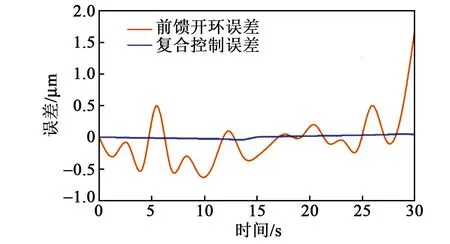
图12 两种控制方法下的误差对比

根据参考国标GB/T 38614—2020的测试标准,测量结果表明,在设计的复合控制系统控制下,压电陶瓷定位平台正、反向重复定位精度分别为0.013 1 μm和0.015 5 μm,准确度为0.033 5 μm,计算出反向差值后可得迟滞误差为0.013%。

5 结束语

针对压电陶瓷位移平台固有的迟滞非线性会降低其定位精度的问题,本文提出一种带有前馈补偿的复合型闭环控制系统。设计一种分段式P-I模型作为前馈补偿,建模误差率小于0.69%。为了提高平台的控制精度提出了一种串联式PI控制电路。为了提高系统的抗干扰能力,检测回路采用双极板电容式传感器,并增加A/D转换电路使其信号数字化,以便存储和运输。根据GB/T 38614—2020 进行实验测试,结果可得出迟滞模型的拟合精度得到提高,控制精度更准确。最终验证了本文所提出的复合控制系统的准确性和有效性。