基于柔度范数差曲率的桥梁损伤定位
朱秀清
(广州市盛通建设工程质量检测有限公司 广州 510075)
0 引言
随着我国经济的发展,桥梁设计的水平日渐提高[1],桥梁作为重大生命线工程,对城市的发展具有重要的促进作用。当桥梁出现损伤未及时修复,会给桥梁带来很大安全隐患,因此桥梁结构健康监测就显得十分重要[2-3]。运营期间桥梁的损伤识别问题作为健康监测系统中的重要组成部分,近年来得到了学者的广泛关注[4]。目前大多数损伤识别问题都是基于模态参数进行的,如唐盛华等人[5]提出基于模态柔度矩阵曲率范数差损伤新指标,再根据梁式结构刚度和位移曲率的负相关关系,推导出准确定量损伤程度的理论表达式,对多个工况进行了定量分析;XIN 等人[6]基于能量算子和小波变换对模态振型曲率定义损伤指标,同时进行数据融合算法来进行损伤检测;GHOSH 等人[7]基于高阶振型及其导数定义了损伤指标,通过数值模拟和实验验证该指标损伤识别效果;李杰等人[8]基于广义柔度对角指标对一梁桥结构进行损伤识别,结果表明该方法可以准确识别三跨连续刚构桥主梁损伤位置和损伤程度;闫天红等人[9]提出了一种基于模态柔度和有限元模型修正相结合的结构损伤识别方法;骆紫薇等人[10]基于范数归一化与稀疏正则化约束提出了一种结构损伤检测方法;RAMESH 等人[11]提出一种基于模态振型曲率平方的新方法来识别损伤;YOON 等人[12]通过曲率模态数据与平滑数据的绝对差值定义损伤指标来建立置信水平实现识别损伤的目标。以上基于模态参数损伤识别的方法各自存在不足之处,其中单独基于曲率模态进行识别损伤的方法容易受模态节点和噪声的影响;而部分指标还需要建立有限元模型并且进行模型修正,损伤检测效率较低;除此之外,单独基于柔度矩阵进行损伤识别方法普遍存在指标量级过低,易受其它因素干扰的缺点。
为了克服以上缺点,本文结合了柔度矩阵、范数和曲率的优点,提出了柔度范数差曲率的损伤指标来识别损伤位置。通过对一简支梁进行数值模拟,检验不同损伤位置、损伤程度和噪声水平对该指标损伤识别效果的影响。
1 理论基础
1.1 柔度矩阵
柔度反映了结构的固有属性,相对于刚度对结构损伤更加敏感,因此许多学者基于柔度矩阵提取损伤指标来定位损伤位置。PANDEY 等人[13]提出结构的柔度矩阵F可近似表示为
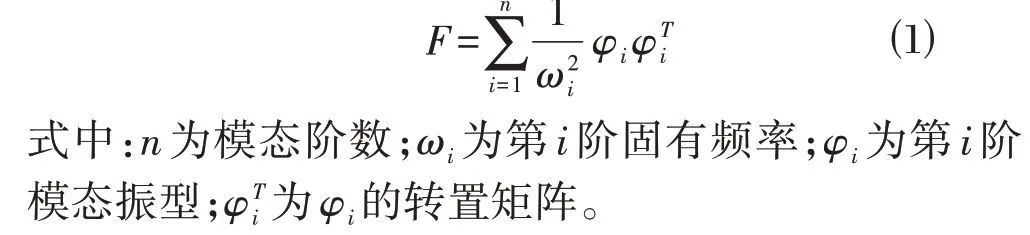
从式⑴可以看到,柔度矩阵F与频率的平方成反比,因此频率对柔度矩阵的贡献随着阶数的增大而减少,即高阶模态信息对柔度矩阵的影响是有限的,本文中取前两阶模态信息进行分析,以此计算柔度矩阵。
1.2 范数
2 型范数是范数里使用较为广泛的范数指标,其本质意义是向量的长度,可以用来衡量向量之间的差异性,实现不同向量的比较。2型范数公式表达为
式中:m和y分别为柔度矩阵的行数与列数。
1.3 曲率
通过中心差分近似计算曲率,曲率公式表达为
式中:φ''ℎ代表第ℎ 个数据的曲率值;l代表两个相邻数据之间的间隔距离。
1.4 损伤指标的建立
通过式⑴建立损伤前后的柔度矩阵,再对柔度矩阵求解2 范数可得到对应的向量,该向量可衡量损伤前后的差异程度,将损伤前后求得的范数作差可得
式中:V为范数差;normℎ和normd分别为结构损伤前后求得的范数。
由于考虑到曲率对结构损伤前后差异变化具有较高敏感性,因此再对范数差求解对应的曲率,可得柔度范数差曲率损伤指标,其公式表达为
2 数值模拟
2.1 模型建立及参数设置
通过ANSYS有限元软件建立一梁桥有限元模型,两端边界条件设置为简支,沿着梁桥长度方向划分为400 个单元,将模型材料设置为钢材,即材料密度为7 850 kg/m3,泊松比为0.3,弹性模量为210 GPa。简支梁截面设置为矩形,梁长设置为L=10 m。简支梁的模型简化图如图1所示。为了更好地研究损伤对简支梁的影响,通过使用软件的删除命令来删除部分单元格,以此来制造损伤。将一移动质量块作为桥梁的移动荷载,使其匀速移动通过桥面。

图1 简支梁模型简图Fig.1 Sketch of the Simple Bridge Model
通过设置不同的损伤位置和损伤程度来研究损伤对梁桥的影响情况,分别在0.4L和0.7L两个位置制造损伤进行工况的组合,以及设置了3 个不同的损伤程度,分别为10%、20%和30%。损伤工况的具体情况如表1所示。

表1 损伤工况Tab.1 Damage Scenarios
2.2 单损模拟结果
当结构发生损伤后,结构的柔度范数差曲率损伤指标曲线会在损伤位置出现突起,以此来实现损伤位置识别的目的。为了研究在不同损伤程度和损伤位置下的单一损伤的情况,分别计算表1 中的工况1~工况3 三个单损工况的柔度范数差曲率损伤指标,损伤识别结果如图2 所示。通过图2 可以看到,在0.4L损伤位置处,损伤指标曲线出现一个明显的突起,这表明该损伤指标能够很好识别到0.4L位置处的损伤。
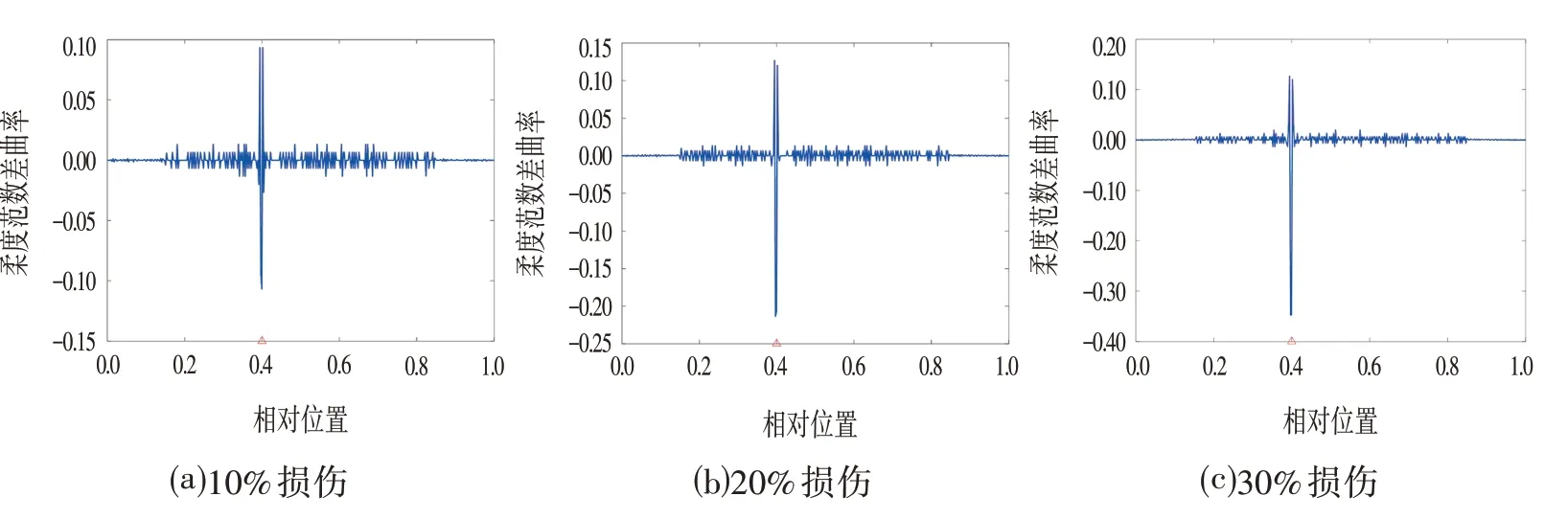
图2 在0.4L损伤位置的识别结果Fig.2 Identification Results with Damage Location at 0.4L
为了验证该方法在不同损伤位置的有效性,通过计算表1中的工况4~工况6三个单损工况的柔度范数差曲率损伤指标,损伤识别结果如图3 所示。由图3可知,在0.7L损伤位置处,损伤指标曲线出现一个明显的突起,这表明该损伤指标能够很好识别到0.7L位置处的损伤。而且从图2 和图3 可以看到,随着损伤程度的增大,柔度范数差曲率损伤指标值也在增大,因此可以通过损伤指标值来比较不同工况下的损伤程度。
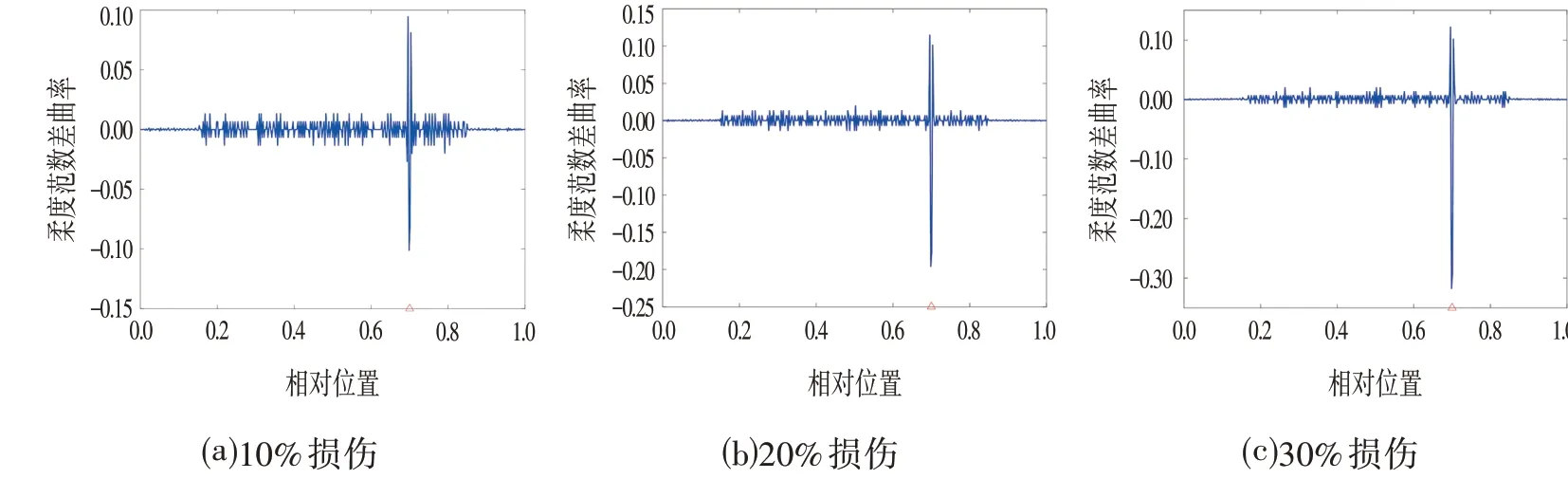
图3 在0.7L损伤位置的识别结果Fig.3 Identification Results with Damage Location at 0.7L
2.3 双损模拟结果
为了研究在不同损伤程度和损伤位置下的双损情况,分别计算表1 中的工况7-工况8 两个双损工况的柔度范数差曲率损伤指标,损伤识别结果如图4 所示。通过图4 可以看到,在0.4L和0.7L两个损伤位置处,损伤指标曲线出现两个明显的突起,这表明该损伤指标能够很好识别 到0.4L和0.7L位置处的损伤。而且从图4 可以看到,随着损伤程度的增大,柔度范数差曲率损伤指标值也在增大,因此可以通过损伤指标值来比较不同工况下的损伤程度。

图4 双损的识别结果Fig.4 Identification Results of Multiple Damages
2.4 噪声鲁棒性
在实际工程中会有各种噪声因素的影响,导致损伤指标的判断失效。因此,为了更加符合实际工程的应用,对模态分析得到的模态振型分别添加100 dB和120 dB 的高斯白噪声,再进行损伤指标的计算。用来衡量噪声水平的信噪比(SNR)可以定义为
式中:SNR单位为信噪比(dB);s(i)为待分析信号;n(i)为噪声信号;As为信号s(i)的均方根;An为信号n(i)的均方根;lg(·)代表对括号内数据求对数。
将单损一个工况作为分析对象,分别计算120 dB和100 dB噪声水平下的工况4的柔度范数差曲率损伤指标,可得损伤指标对应曲线,识别结果如图5 所示。通过图5可以看到,在0.7L损伤位置处,损伤指标曲线出现一个明显的突起,这表明该损伤指标能够很好识别到0.7L位置处的损伤。将双损一个工况作为分析对象,分别计算120 dB 和100 dB 噪声水平下的工况7的柔度范数差曲率损伤指标,可得损伤指标对应曲线,识别结果如图6 所示。通过图6 可以看到,在0.4L和0.7L损伤位置处,损伤指标曲线出现两个明显的突起,这表明该损伤指标能够很好识别到0.4L和0.7L位置处的损伤。因此,该方法具有一定的噪声鲁棒性。

图5 噪声影响下单损识别结果Fig.5 Identification Results of Single Damage under the Influence of Noise

图6 噪声影响下双损识别结果Fig.6 Identification Results of Multiple Damages under the Influence of Noise
3 结论
本文基于柔度矩阵计算范数差曲率,以此得到柔度范数差曲率损伤指标来进行损伤识别,并且检验了该方法在不同损伤位置、损伤程度和噪声影响下的效果。主要结论如下:
⑴本文提出的损伤指标能够准确识别单损和双损不同工况下的损伤位置,并且可以通过指标值的大小来比较损伤程度大小;
⑵本文提出的损伤指标在噪声影响下仍然具有良好识别效果,具有实际工程的应用前景。

