天线座扭转振动固有频率分析*

李德举，黄 河

（中国电子科技集团公司第二十九研究所，四川成都 610036）

引 言

天线座作为支撑并驱动天线等载荷回转的机械类装备有着广泛的应用。天线座的动力学特性直接影响着载荷的指向精度、稳定时间等动态性能，而天线座扭转维度的固有频率是动态性能最直观的指标。

文献[1]采用牛顿法对天线座驱动系统的扭转振动谐振频率进行了计算；文献[2]采用霍尔兹法分别对某型舰载雷达天线传动系统的固有频率进行了计算；文献[3]同样采用霍尔兹法对某型天线座前5阶的扭转振动固有频率进行了计算；文献[4]对位标器传动装置的固有频率和模态进行了分析，并对传动装置进行了优化；文献[5]采用拉格朗日法建立了某天线座的多柔体动力学模型，得到了天线座中齿轮副的动力学响应，并通过ADAMS进行了仿真分析，所得结果与试验结果一致。本文以方位转台式天线座为研究对象，基于拉格朗日法创建动力学方程，得到扭转振动固有频率的解析表达式，使用ADAMS软件仿真分析了天线座的固有频率，并与理论分析结果进行了比较。

1 天线座组成及工作原理

某方位转台式天线座的组成和外形分别如图1和图2（除去了负载及平台）所示。天线座的传动原理如下：交流伺服电机提供动力，经减速器将动力传递给输出端小齿轮，小齿轮与转盘轴承内圈上的内齿啮合，从而驱动与内圈固连的负载转动。其中，减速器为直角型式，转盘轴承外圈与基座及车平台固连，内圈与转盘及负载固连。

图1 天线座组成

图2 天线座外形

2 基于拉格朗日法的固有频率计算

在天线座设计之初，通常对振型关注度不高，只需求解扭转振动固有频率，为伺服系统设计师和总体设计师提供参考。

为便于分析，将天线座视为一线性定常系统，用拉格朗日法建立其动力学模型。拉格朗日法从功能平衡角度出发，根据动能与势能之差建立拉格朗日函数。不考虑系统损耗时，动力学方程的基本形式为：

式中：t为时间；qi为广义坐标；L为拉格朗日函数，L=T-U（T为系统的动能，U为系统的势能）；Fi为广义力。

在选取广义坐标后，求得各部分的动能、势能、拉格朗日函数及其偏导数，再通过系数矩阵形式描述动力学方程，即可求解固有频率。

2.1 动力学模型

2.1.1 广义坐标

假设负载、车平台等构件为刚体，忽略摩擦、侧隙等非线性因素，只考虑电机、减速器的势能，并将电机和减速器的扭转刚度视为恒定值。

在描述系统动能和势能时，考虑天线座中伺服电机输出端、减速器输出端及末级的转角、角速度、角加速度，选取构件的转角θi为广义坐标，令各构件的惯量为Ji，扭转刚度为Ki，下标i与图1中的构件编号对应。减速器的速比为n2，转盘轴承内齿与小齿轮之间的速比（末级速比）为n4。

天线座的原理框图如图3所示。实际使用时，无论天线座扇扫、圆扫还是驻留，伺服电机接收驱动器指令后，电机转子的运动均已确定，故电机端应为约束状态。

图3 天线座原理框图

2.1.2 系统动能

系统的动能为各部件动能之和：

2.1.3 系统势能

系统的势能为电机与减速器势能之和：

2.1.4 拉格朗日函数及偏导数

根据式（2）和（3）可得拉格朗日函数：

式中：T1和T7分别为伺服电机和负载的动能；Jε1=

写成如下矩阵形式：

惯量矩阵J和刚度矩阵K分别为：

2.1.5 固有频率

天线座的扭转振动频率可简化为求解特征值方程问题：

即：

式中，ω为扭转振动圆频率。

式（9）的解析解较为复杂，可通过已知参数代入，便可得到两阶扭转振动频率。

2.2 考虑平台扭转刚度的动力学模型

若考虑其他弹性环节，可引入相应的广义坐标，建立对应的运动学方程。例如，考虑天线座安装平台的扭转变形影响，需计入平台的转角θ9、扭转刚度K9、转盘轴承外圈、基座和平台的转动惯量J5，J8和J9，则式（2）调整为：

式（3）调整为：

通过比较引入平台扭转刚度前后的结果可知：

1）式（9）与式（12）中a11，a12，a21和a22四个元素完全相同，除元素a33外，其他元素为0。故式（12）得到的三阶频率中两阶与式（9）相同；

其中，平台的转动惯量J9在动态过程中的具体数值与平台构型、质量分布密切相关，无法准确量化。对此，可采用仿真的方法进行分析。

3 基于ADAMS的仿真分析

除了采用数学模型对天线座的扭转振动频率进行计算外，还可以采用实体模型，在多体动力学软件中进行仿真分析，并与数学模型求得的结果互相验证。本文基于多体动力学分析软件ADAMS，对天线座进行动力学建模，并求解扭转振动固有频率。

3.1 模型前处理

天线座由诸多零部件构成，为提高仿真效率且保证计算的准确性，需要对模型进行一定程度的简化。

首先要去除对仿真结果影响很小的螺钉等紧固件，再基于统一坐标系，将具有同样运动状态且为相同材料的实体整合为一个构件。基座、转盘轴承、转盘、小齿轮为真实状态的物理模型。电机、减速器、负载由多种材料组成，且本文并非研究部件特性，所以根据它们的实际重量、重心和惯量，通过圆柱实体表征即可。

此外，在建立运动副时，常常要用到依附于构件的Marker点，所以需要提前确定这些点的坐标，包括转盘轴承内齿与小齿轮齿宽中面上分度圆切点的坐标、小齿轮齿宽中面与回转轴的交点等。

以上操作建议在三维建模软件中进行，再将简化后的模型转化为.x_t格式的文件，导入Adams View环境中。

3.2 仿真设置

仿真设置主要包括赋予部件材料及质量特性，建立运动副，施加载荷、驱动等。

3.2.1 物理特性定义

转盘和基座的材料为铝合金，转盘轴承和齿轮的材料为合金钢，赋予相应密度即可。

3.2.2 运动副创建

模型中运动副包括小齿轮与减速器之间的转动副，转盘轴承内圈与外圈之间的转动副以及小齿轮与转盘轴承内圈之间的齿轮副。齿轮副可采用关联以上两旋转副与分度圆上Marker点的方式创建，或在机构模块中创建。前者按照理论传动比传递运动和动力，后者的选择更多，需考虑啮合状态、接触等因素影响，本文暂不考虑这些非线性因素，故选用第一种方法进行创建。

电机轴由圆柱实体提供惯量，其输入端与大地之间构成转动副，输出端通过扭簧与减速器输入端连接，以模拟电机轴扭转刚度；减速器内部轮系由一级齿轮副代替，以模拟其速比，其输出端与小齿轮之间通过扭簧连接，以模拟扭转刚度。

另外，在上述扭簧的设置中，不应忽略阻尼系数，否则会在固有频率处产生共振，末端响应会趋于无穷。电机阻尼系数受内部磁路、轴承参数等影响，减速器阻尼系数受齿轮与轴承参数、润滑脂类型等影响，可通过试验或计算得到。考虑到这并非本文关注的重点，故参照文献[6]中数据，设定阻尼系数为100 N·mm·s/(°)，使得末端响应不发散即可。

3.3 运动学分析

在进行动力学仿真之前，先对模型进行运动学验证，以保证各运动副的正确性。图3中天线座的参数见表1。

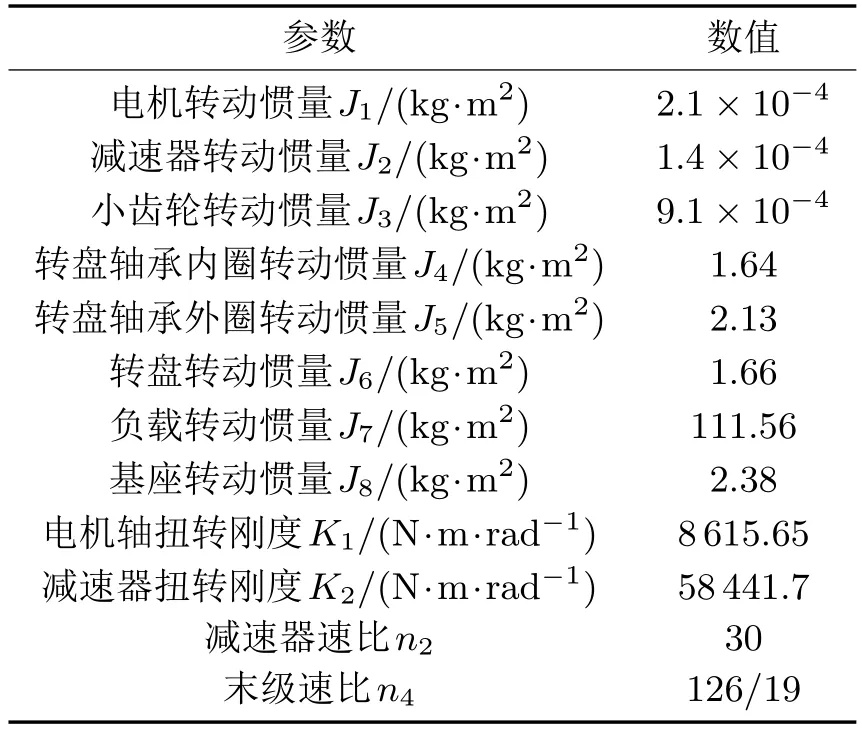
表1 天线座参数

依照3.1和3.2节中所述的步骤，建立除平台以外的天线座实体模型。先将系统中扭簧抑制，扭簧两端构件直接固连，然后在电机输出端施加1 000°/s的转速驱动。

设置仿真时间2 s，100个载荷步。仿真结果如图4所示。根据速比关系，转盘的角速度应为5.026 5°/s，负载转角与理论结果吻合。

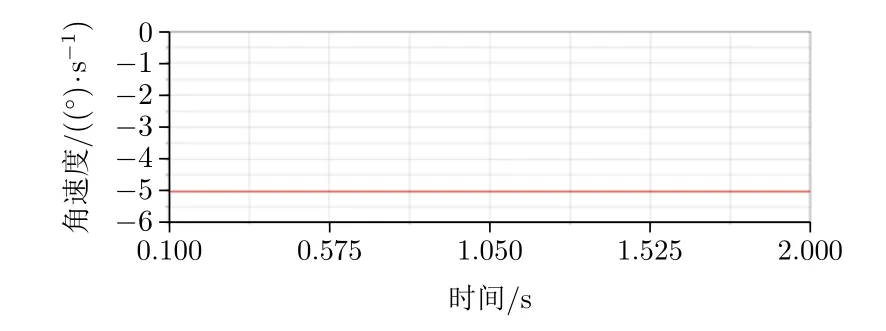
图4 天线座运动学仿真

3.4 动力学分析

在进行动力学仿真之前，激活电机及减速器输出端的扭簧。然后在电机输出端使用SWEEP命令施加正弦扫频驱动，由于频段较宽，故分为0～750 Hz和750～1 500 Hz两段进行扫频，这使得频域的结果更便于分析。

负载的扭转维度角速度响应如图5所示，对响应进行快速傅里叶变换，结果如图6所示。

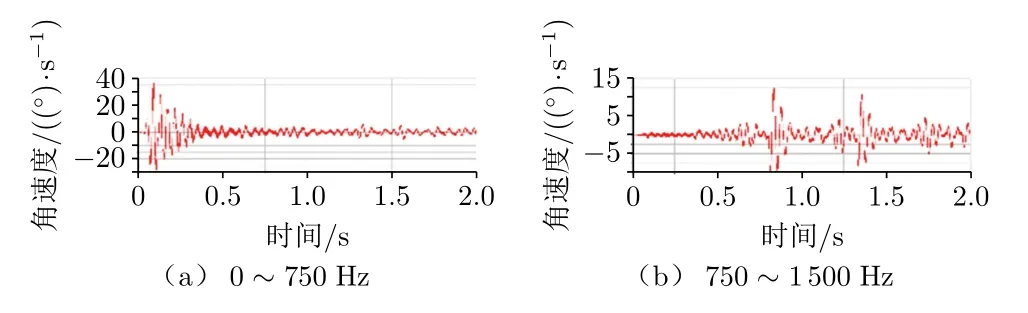
图5 两频段角速度响应

图6 响应的快速傅里叶变换

仿真得到的两阶固有频率分别为23.29 Hz和1 059.25 Hz，采用式（9）计算，结果为23.71 Hz 和1 023.22 Hz，两者之间的偏差源于前文提及的阻尼系数的影响。

3.5 刚柔耦合动力学分析

考虑到平台转动惯量无法准确评估，故将平台实体模型柔性化，并与天线座连接，进行刚柔耦合动力学分析。其原理是采用有限元方法，通过计算构件的自然频率和对应的模态，按照模态理论，将构件产生的变形看作是由构件模态通过线性计算得到的[7]，但构件的模态信息需借助其他有限元软件得到。

本文通过ANSYS APDL对平台划分网格，定义基座与平台连接的各螺栓孔中心为刚性节点，求解平台前6阶模态，并输出.mnf格式文件至ADAMS中进行装配，如图7所示。

图7 天线座与平台装配示意图

由于平台模态已通过ANSYS得到，其1阶固有频率为106.3 Hz。天线座与平台装配形成新的系统后，局部刚度和转动惯量发生变化，故需关注平台1阶固有频率周围是否出现图6所示结果以外的固有频率。施加0～200 Hz频段的扫频驱动，响应及其快速傅里叶变换结果如图8所示。

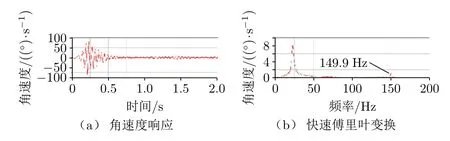
图8 角速度响应及快速傅里叶变换

从图8可以看出，天线座扭转振动的2阶固有频率为149.9 Hz，由此可知引入平台的系统动态特性产生了较大变化，在实际应用中不应忽略平台的影响。

4 结束语

本文首先基于拉格朗日法建立了一典型天线座的扭转振动动力学模型，并分析了系统存在两自由度、三自由度时固有频率的解析表达式；介绍了基于ADAMS的动力学分析流程，并创建实体模型分析了该天线座的固有频率，所得结果与理论分析的结果吻合，验证了解析解的正确性。这为伺服控制系统算法优劣的评估、参数的调整以及机电联合仿真打下了一定的基础。