BP 人工神经网络对庄河大骨鸡剩余保质期的预测
王琦 崔妍 梁健健 薛伟锋
(大连海关技术中心 辽宁大连 116000)
0 引言
庄河大骨鸡因其肉质鲜美而深受消费者欢迎。大骨鸡年饲养量约为230 万只, 其中小规模散养及庭院饲养量高达200 万只[1]。 散户饲养的大骨鸡被宰杀后多以热鲜鸡的形式存在。热鲜鸡营养丰富,在存放过程中其感官、 理化和生物指标都会发生较大改变,这些变化会直接影响大骨鸡的品质,甚至造成食品安全事故。鉴于此,有效预测大骨鸡的保质期具有重要意义, 预测模型的发展为保质期的预测提供了一种有效的技术手段。
对于保质期预测模型的研究, 主要包括基于化学动力学[2-4]、微生物生长动力学[5-6]、温度[7]、统计学[8]和数据分析[9-12]等方法。 目前,已报道的大骨鸡保质期预测模型主要是基于全面稳定性指数(global stability index,GSI) 理论构建的多因素动力学模型[13],反映的是温度对大骨鸡综合品质的影响, 符合热力学反应规律,具有零级和一级动力学反应公式。该模型通过将大骨鸡感官品质、 物理化学和微生物方面多个指标整合为一个综合指标, 全面考察大骨鸡品质变化, 有效避免了单个指标保质期预测模型的片面性。 尽管GSI 模型能够准确预测大骨鸡在多个品质指标和存放温度下的保质期, 但当大骨鸡品质参数越发多样、存放温度不断变化时,该模型需要人为连续重复运算整个建模过程,非常耗时,不利于大范围推广应用。反向传播(back propagation,BP)人工神经网络是应用最广泛的人工智能建模方法, 可通过自学习、 网络训练的方式很好地解决多指标预测的问题, 与传统动力学模型相比,BP 模型预测食品保质期具有更高的精度, 已被广泛应用于食品保质期预测领域[14-16],但在尚未见应用于大骨鸡保质期预测方面的研究。鉴于此,本研究以文献[13]中报道的大骨鸡保质期实验测定数据为基础, 构建大骨鸡剩余货架期的BP 人工神经网络模型, 并验证该模型的可靠性,并将BP 模型预测结果与文献[13]中使用的基于动力学构建的全面稳定性指数理论模型获得的结果进行比较, 判断BP 神经网络模型在预测大骨鸡保质期方面是否具有优势。
1 模型构建方法
BP 人工神经网络一般由输入层、隐含层和输出层3 个部分构成[17],层与层之间采用全互联的连接方式,而同层单元间却无相互联系[18]。 BP 人工神经网络基于训练过程校正误差而向后传播, 即误差计算在输出层,向后依次传播至隐含层和输入层,隐含层包含充足、连续的预测问题[19-20]。
1.1 网络结构的选择
BP 神经网络能学习和存储大量的输入—输出模式映射关系, 无需事前了解描述这种映射关系的数学方程, 只要能提供足够多的样本供BP 网络进行学习训练,它便能完成由n 维输入空间到m 维输出空间的正确映射[21-22]。 一个由输入层、隐含层和输出层构成的3 层BP 人工神经网络即可完成上述映射[21-22]。因此,本研究选取具有单个隐含层的3 层BP人工神经网络。
1.2 输入输出层参数确定
针对大骨鸡存放过程中营养参数的变化情况,达到对大骨鸡剩余保质期 (剩余保质期=已知保质期-已存放时间)进行预测,模型设计如图1 所示。其中,大骨鸡的存放温度、感官得分、汁液流失率、菌落总数和挥发性盐基氮等5 项作为模型输入层神经元,大骨鸡的剩余保质期作为输出层神经元。 BP 神经网络的隐含层节点数对BP 神经网络预测精度有较大的影响, 但目前还无法找到一个普遍适用的理想方法确定隐含层神经元数[23]。节点数太少,网络不能很好地学习,需要增加训练的次数,训练的精度也受到影响;节点数太多,训练时间增加,网络容易过度拟合[24]。 目前常用的隐含层参考式(1)[25]:
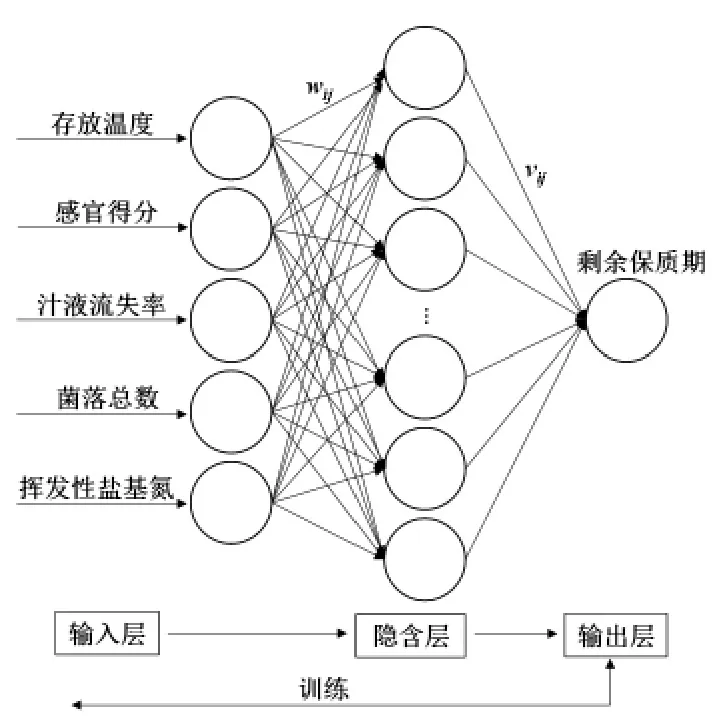
图1 BP 神经网络结构Fig.1 BP neural network structure
式中,N—隐含层神经元数;m—输入层神经元数;n—输出层神经元数;a—1~10 之间的常数。
本研究使用Matlab 2019b 软件对网络隐含层节点数为3~12 时的性能进行测试,结果表明,隐含层节点数为5 时, 网络收敛速度最快, 均方误差最小,故本研究的模型隐含层节点数选择5。
1.3 网络函数选择
BP 人工神经网络中包括传递、训练、学习、网络性能和仿真函数等。 BP 网络的传递函数有多种,包括log-sigmoid 型函数logsig、tan-sigmoid 型函数tansig,以及线性函数purelin,其中sigmoid 型传递函数的曲线形状都是S 型的,log-sigmoid 和tan-sigmoid 型函数均是如此。 logsig 函数的输入值可取任意值,输出值在0 和1 之间;tansig 函数的输入值同样可取任意值,但输出值在-1 到+1 之间;线性传递函数purelin 的输入和输出值可取任意值。本研究隐含层传递函数选取tansig, 输出层传递函数则使用purelin。 trainlm 函数收敛快、误差小,而且训练效果好, 因此本研究采用该函数作为训练函数。 为避免BP 神经网络在批处理训练时会陷入局部最小,且提高网络训练速度, 采用附加动量法构建BP 神经网络,选取learngdm 为学习函数,该函数为梯度下降学习函数,利用神经元的输入和误差、权值和阈值的学习速率和动量常数计算权值或阈值的变化率。
1.4 网络训练
动量常数采用函数默认值0.9, 学习速率为0.01,网络性能目标误差为10-7,训练的最大步数为5 000。 如表1 所示,将存放温度、感官得分、汁液流失率、菌落总数、挥发性盐基氮和剩余保质期等6 个参数的所有数据(标注* 数据除外)作为训练集,按照上述方法构建BP 人工神经网络模型, 标注* 数据用于验证模型的准确性。 进行BP 模型验证之前,需要将检验输入数据归一化, 然后再将得到的数据反归一化,从而获得标注*数据对应的剩余保质期。
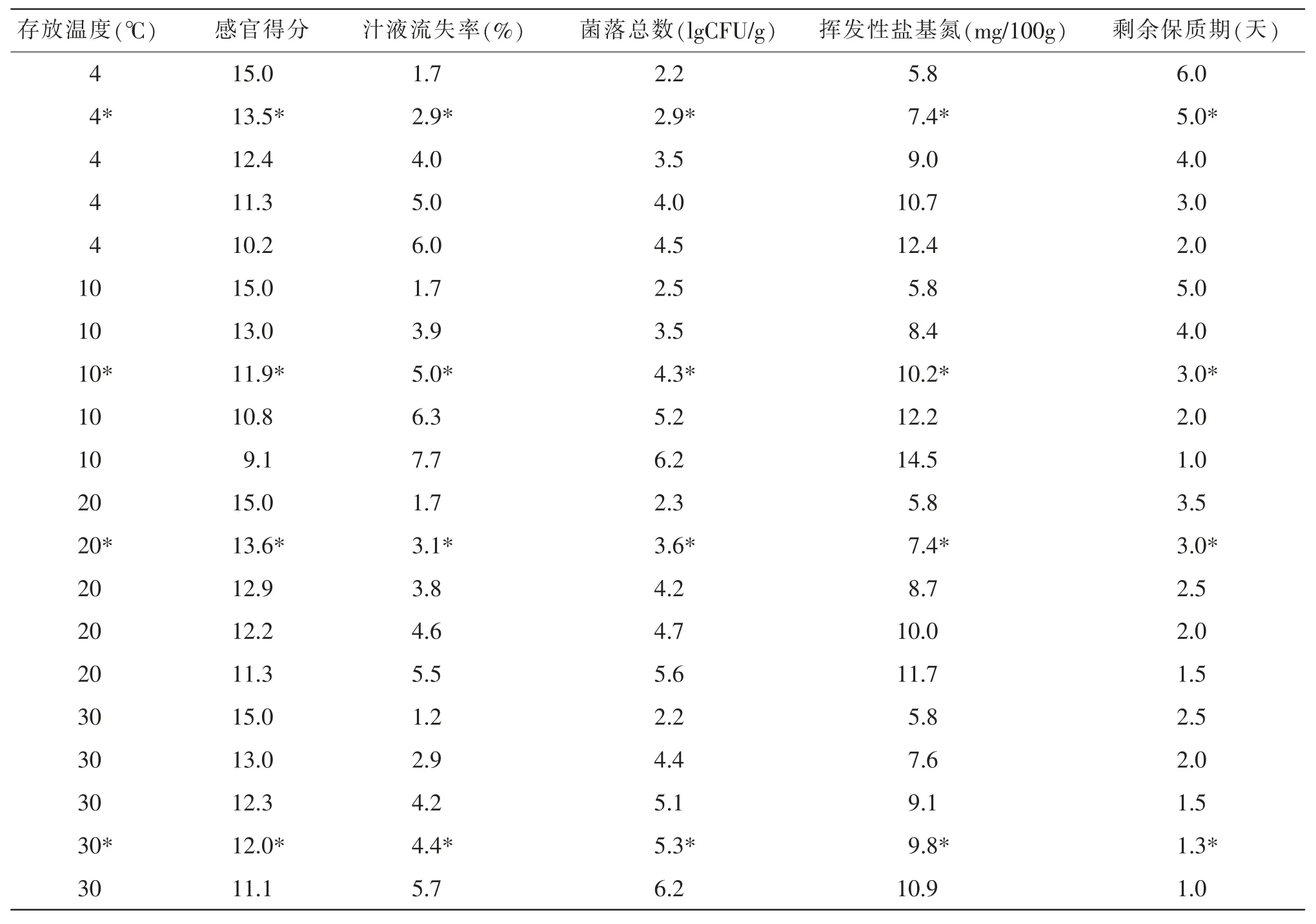
表1 大骨鸡鸡肉品质评价指标结果Table 1 Results of quality evaluation index of Dagu chicken
2 结果与分析
2.1 BP 神经网络模型程序设计
Matlab 程序语言如下:
2.2 BP 神经网络模型训练结果
将模型构建数据输入设定好的网络模型中,经11 次迭代后网络性能误差为1.9×10-9, 满足误差设定要求而停止训练, 结果如图2 所示。 均方误差(mean square error,MSE)用来评价网络模型是否合适,该值越小,说明模型性能越好;相关系数R 值用来描述实际值和模型预测值之间的线性相关性。 本研究构建的BP 神经网络模型的MSE 和R 如图3所示, 说明该BP 模型可以用于大骨鸡剩余保质期预测。

图2 BP 神经网络模型训练图Fig.2 Training plot of BP neural network model

图3 BP 神经网络模型训练结果Fig.3 Training results of BP neural network model
2.3 模型预测结果比较
经过训练后, 获得标注*数据对应的剩余保质期如表2 所示。与文献[13]结果比较,发现使用全面稳定性指数(GSI)模型预测4℃~30℃下大骨鸡剩余保质期的误差为2.0%~15.4%,而采用BP 人工神经网络模型预测剩余保质期的误差仅为0%~7.7%,说明BP 人工神经网络模型与全面稳定性指数模型相比,能更加准确地预测大骨鸡的剩余保质期。 该BP 模型的建立,能更加准确、快速的预测出不同存放温度下大骨鸡剩余保质期,具有广泛的应用前景。

表2 GSI 理论模型与BP 神经网络模型预测大骨鸡剩余保质期结果比较Table 2 Comparison of GSI theory model and BP neural network model in predicting the remaining shelf life of Dagu chicken
3 结论
本研究采用BP 人工神经网络模型预测大骨鸡剩余保质期,发现该模型预测结果较为准确,可以很好地应用于食品剩余保质期的预测。 但建立的BP神经网络模型也存在不足,当存放温度升高后,预测的剩余保质期误差会明显增大, 可能是样品分析次数较少,获取有效数据不足引起的。如果增加高温条件下样品检测数量并缩短在高温环境下检测样品的时间间隔,可能会提高该模型的精度。本研究建立的BP 人工神经网络模型, 对热鲜鸡在正常环境温度(4℃~30℃) 下的剩余保质期具有良好的预测能力,为大骨鸡生产、包装、销售和食用安全提供了一种有效的保质期监管手段。

