华东地区地面和高空风场的多模式集成精细化预报研究

智协飞,吴柏莹,罗忠红,曹晴

① 南京信息工程大学 气象灾害教育部重点实验室/气象灾害预报预警与评估协同创新中心,江苏 南京 210044;

② 天气在线气象应用研究所,江苏 无锡 214000;

③ 中国民用航空局 空中交通管理局厦门空中交通管理站,福建 厦门 361006;

④ 中国民用航空局 华东地区管理局,上海 200335

20世纪中后期以来,随着电子计算机技术和大气理论的发展和进步,数值天气预报技术取得了长足进展,有效地提高了天气预报的准确性(Baueret al.,2015)。由于大气是高度非线性的混沌系统,数值模式初始场具有不确定性,物理过程参数化方案也不够完善,这些因素导致数值天气预报存在不确定性。为解决这一问题,集合预报应运而生并得到了广泛应用(Leith,1974;杨学胜,2001;李泽椿和陈德辉,2002;杜均,2002;陈静等,2003;智协飞和陈雯,2010;麻巨慧等,2011;王佳等,2012;张涵斌等,2014;智协飞等,2015;张涵斌等,2017;陈超辉等,2018)。目前最具代表性的全球集合预报系统(Global Ensemble Prediction System,GEPS)包括美国国家环境与预报中心(National Centers for Environmental Prediction,NCEP),欧洲中期天气预报中心和加拿大气象局(Canadian Meteorological Centre,CMC),这几个中心所采用的初始扰动方法与集合预报结果都有一定差异。国内外研究指出,多模式超级集合预报的预报效果优于单模式预报和简单集合平均预报(Krishnamurti et al.,1999,2000;林春泽等,2009;智协飞等,2009;Zhi et al.,2012;He et al.,2015;智协飞和黄闻,2019;Ji et al.,2019,2020)。

在航空器飞行的气象保障中,风场的准确预报也至关重要。目前数值模式提供的风场预报还存在较大误差,而且缺乏时空精细化预报资料。在实际应用过程中,通常首先采用插值方法实现格点资料的精细化,常用的方法包括双线性插值、克里格方法、反距离加权法、样条函数等。国内外许多研究针对不同的插值方法进行了比较(Luo et al.,1998;Robeson and Janis,1998;林忠辉等,2002;王亚男和智协飞,2012)。林忠辉等(2002)通过比较三种不同插值方法对不同气象要素的插值结果,发现不同插值方法的适用性是不同的,没有一种插值方法可以适用于所有气象要素。因此,需要通过对比实验来得到最优插值方法。王亚男和智协飞(2012)采用多种插值方法对降水预报进行插值,发现双线性插值和反距离加权法效果较好,且后者略优于前者。

本文基于ECMWF、GRAPES-Meso、GRAPES-GFS、GFS四个中心的华东及周边地区2020年1—4月的风速预报资料,选取最优插值方法进行时空插值,提高风速预报在时间、空间上的精细化程度,将垂直层预报数据从等压面插值到等位势高度面非常规垂直层风场,插值后再进行多模式集成预报试验,建立站点终端管制区空中(约3 000 m)每层300 m共11层风场的智能预报模型,为机场及终端区的飞行保障提供精准的风场预报服务。

1 资料和方法

1.1 资料

1.1.1 模式预报资料

1)ECMWF风场预报资料(纬向风u、经向风v),地面水平分辨率为0.125°,高空各层水平分辨率为0.25°,逐日起报时间为12时(世界时,下同),预报时效为0～72 h,每隔3 h输出一次预报结果。垂直层次主要包括700、850、925、950、1 000 hPa、地面10 m。时间2020年1月13日—4月13日。研究区域110°～130°E、20°～40°N。

2)同期、同区域GRAPES-Meso风场预报资料,各层分辨率均为0.4°,初始场时间间隔为24 h,逐日起报时间为12时,预报时效为0～72 h,每隔3 h输出一次预报结果。垂直层次主要包括700、750、800、850、900、925、950、975、1 000 hPa、地面10 m等。

3)同期、同区域GFS风场预报资料,各层分辨率均为0.5°,初始场时间间隔为24 h,逐日起报时间为12时,预报时效为0～72 h,每隔3 h输出一次预报结果。垂直层次同GRAPES-Meso。

4)同期、同区域GRAPES-GFS风场预报资料,各层分辨率均为0.25°,初始场时间间隔为24 h,逐日起报时间为12时,预报时效为0～72 h,每隔3 h输出一次预报结果。垂直层次同GRAPES-Meso。

1.1.2 再分析资料

用来评估模式预报技巧的观测资料的质量、分辨率、覆盖的地理范围等都应考虑。实测站点资料能更好地反映真实物理量情况,能更加客观地检验多模式集成预报,但是对于格点精度较高的预报资料,观测资料存在不够精细和缺测较多等缺点,容易导致额外的误差。

ERA5资料是ECMWF打造的新一代再分析资料。ERA5在ERA-Interim(Uppala et al.,2008)的基础上有了很大改进,时空分辨率大幅提升,提供的变量也增加到240种。因此,本文选择ERA5资料作为评估用“观测”资料,并选择华东地区几个典型站点的地面自动观测资料作为精细化预报产品释用的辅助评估资料。

ERA5再分析资料:地面10 m风场预报资料的分辨率为0.125°。高空各层风场和位势高度资料,高空层水平分辨率为0.25°,高空垂直层次主要包括700、750、800、850、925、950、975、1 000 hPa等。所取时间和区域同ECMWF预报资料。

1.2 方法

由于各个模式预报资料及观测资料的分辨率并不完全一致,为了得到华东地区更为精细化的气象要素数据,在试验之前需要对数据进行精细化预处理。利用双线性插值方法,将每个中心预测数据的预测时间统一为0～72 h逐1 h,经过比较后,选择反距离加权方法将低分辨率网格预测数据插值到高分辨率网格。本文将每个模型的地面预测值插值到0.125°×0.125°经纬度网格,高空预测值插值到0.25°×0.25°经纬度网格。将高空等压面上风速数据插值到等位势高度层(约为0～3 000 gpm,垂直方向间隔300 gpm)。

得到统一的高时空分辨率风场资料后,基于均方根误差、距平相关系数等评估方法,采用消除偏差集合平均、适用于矢量二维风场订正的扩展复卡尔曼滤波技术等方法对多模式预报数据进行集成。

1.2.1 双线性插值

双线性插值的核心思想是分别在两个方向上各自进行一次线性插值。假设已知某变量场函数的四个点,在X、Y方向上分别进行插值后,得到的两个点再在Y方向上线性插值,即可得到所求的变量。详细计算过程可参考王亚男和智协飞(2012)。

1.2.2 反距离权重法插值

反距离权重法插值(IDW,Inverse Distance Weight),是按照目标站点与已有网格点间的距离反比分配权重,距离较近的数据点权重较高,距离较远的数据点分配的权重较小。

(1)

式中:Z为目标站点的物理量要素;Zi为站点i的要素值;di为与第i个站点的距离;n为站点数;a为反比例系数(一般取2)。

1.2.3克里格插值

克里格法(Kriging)是一种经常使用的地理统计的插值方法,根据特性来选取适当的半变异理论函数。

(2)

式中:λi是用于插值的第i个点的要素值Zi的权重,具体公式参考刘峰(2004)。

1.2.4 三次样条插值

三次样条插值(Cubic Spline Interpolation),又称为Spline插值,是一种多项式插值方法。可以通过一系列平滑曲线的形式值点来完成求解三弯矩方程组的数学过程,在实际计算中,需引入边界条件来完成计算(Hutchinson,1995)。

在区间[xi-1,xi](i=1,2,…,n-1)上,S(x)为:

(3)

其中:mi-1=xi-xi-1,增加自由边界条件:

(4)

(5)

得到S′(x)满足的方程:

μiiS′(xi-1)+2S′(xi)+λiS′(xi+1)=δi。

(6)

其中:

(7)

μ0=0、δ0=δn=0、λn=0代入可求每个子区间的三次样条函数。

1.2.5 多模式集成预报方法

选用多模式滑动训练期消除偏差集合平均(Bias-removed Ensemble Mean,BREM)、和针对矢量二维风场改进后的扩展复卡尔曼滤波方法进行集成预报试验。

本文采用滑动训练期方法,即通过试验选取一个最优训练期长度逐日向后滑动,预报期的第一天为紧接着训练期后的一天,训练期窗口不断滑动,这样就能根据时间变动及时替换各个模式的预报权重,使预报结果更为准确。

卡尔曼滤波不同于常见的线性的多模式集成预报方法,它是一种能够根据每个时次的预报和观测数据,自适应迭代各模式预报的权重系数的非线性方法。此前已有一些研究将该方法应用于气温、降水和台风路径的集成预报中,预报效果明显改善(He et al.,2015;智协飞和黄闻,2019)。

水平风场是一种二维矢量场,我们将它分解为纬向风和经向风。参照He et al.(2015)的研究思路,我们对风场的多模式集成也采用复卡尔曼滤波方法。在ACEKF中,所有的初始矩阵除了观测算子H的长度变为2,宽度扩展了1倍之外,其余向量长度均扩展了1倍,宽度变为2。

(8)

相应的,预报期中的预报方程为:

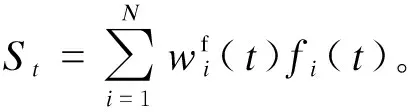
(9)

1.2.6 均方根误差

采用均方根误差(Root-Mean-Square Error,RMSE)对单模式预报和多模式集成预报进行评估,其计算方法如下:

(10)

式中:N是区域格点总数;Fi为样本i的预报值;Oi为样本i的观测值。均方根误差的数值越小,实测值和预报值的差距越小,表明预报越准确。

2 风场预报时空插值方法对比检验

2.1 水平插值

为了统一各模式初始数据的水平分辨率,并获得更精细化的风场预报资料,利用克里格、三次样条、双线性和反距离加权插值等4种插值方法对不同模式的预报资料进行水平插值,将数据统一插值到0.125°×0.125°分辨率(地面)和0.25°×0.25°分辨率(高空),并比较这4种插值对风场预报的影响。反距离加权插值方法和克里格插值方法的加权系数都是距离的函数,引入地理信息使得水平插值效果更优,反距离加权插值方法在计算中不需要对每一个待插值点求解一个线性方程组,用到的存储空间比较小,计算较为方便。首先,利用GRAPES-Meso的模式预报资料作插值试验。图1给出4种水平插值方法得到的地面纬向风预报的均方根误差,其中反距离加权插值方法的均方根误差最小,为2.134 m/s,而三次样条插值方法的均方根误差最大,达2.198 m/s,双线性插值和克里格插值方法得到的地面纬向风场预报均方根误差介于三次样条插值和反距离加权插值的预报均方根误差之间。地面经向风也有类似的特征,即反距离加权插值方法的均方根误差最小,而三次样条插值方法的均方根误差最大(图2)。双线性插值和克里格插值方法得到的地面经向风场预报均方根误差非常接近。

图1 GRAPES-Meso模式预报期内华东区域预报时效为24 h的地面10 m纬向风经克里格(a)、三次样条(b)、双线性(c)、反距离加权(d)插值后的均方根误差(单位:m/s)的地理分布Fig.1 Geographical distribution of RMSEs(units:m/s) in GRAPES-Meso 24-hour surface zonal wind forecasts over East China for the period from January to April 2020,using (a) Kriging,(b) Cubic Spline,(c) Bilinear,and (d) IDW interpolation methods

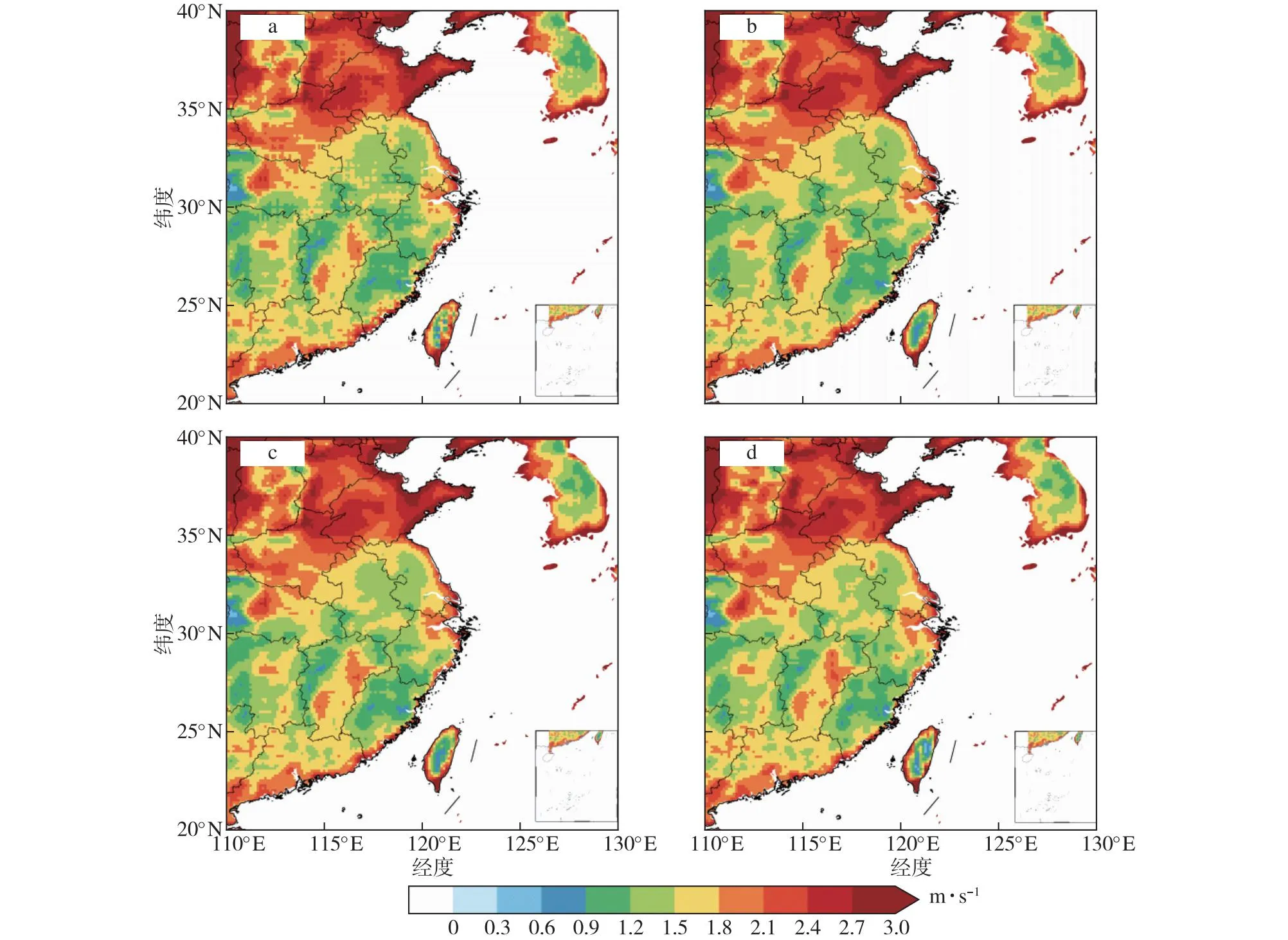
图2 GRAPES-Meso模式预报期内华东区域预报时效为24 h的地面10 m经向风经克里格(a)、三次样条(b)、双线性(c)、反距离加权(d)插值后的均方根误差(单位:m/s)的地理分布Fig.2 Geographical distribution of RMSEs (units:m/s) in GRAPES-Meso 24-hour surface meridional wind forecasts over East China for the period from January to April 2020,using (a) Kriging,(b) Cubic Spline,(c) Bilinear,and (d) IDW interpolation meyhods

由图3可知,1月份风速的预报准确率较高,相比经向风,纬向风的预报准确率更高。反距离加权插值方法在各个月份,都表现出了明显的优势。相较效果最差的三次样条插值方法,反距离加权插值的预报均方根误差减小了16%。此外,高空水平插值后的结果与地面基本一致(图略),因此后面各模式水平插值都采用反距离加权插值。

图3 GRAPES-Meso模式在预报期内,华东区域24 h地面10 m纬向风(蓝色)、经向风(黄色)预报在1月(a)、2月(b)、3月(c)、4月(d)经克里格、三次样条、反距离加权和双线性插值后的区域平均均方根误差(单位:m/s)Fig.3 Regional average RMSEs(units:m/s)of GRAPES-Meso 24-hour wind forecasts over East China,where blue and yellow bars denote zonal and meridional wind forecasts,respectively,in (a) January,(b) February,(c) March,(d) April of 2020,using Kriging,Cubic Spline,IDW,and Bilinear interpolation techniques

2.2 垂直插值

为建立风场智能化预报模型,输出从地面到高空(约3 000 m)每层300 m共11层的非常规垂直层风向风速,方便更好地分析风向、风速随高度的变化。将WRF自带的线性垂直内插方法应用于4个模式预报资料的垂直插值。首先利用ECMWF模式预报资料作插值试验,将拥有三维变量的风场数据插值到给定的气压层或高度。将高空各模式预报数据和与之时空尺度对应的ERA5再分析数据从等压面(1 000～600 hPa)插值到等位势高度面上(300～3 000 pgm),采用ERA5再分析资料的位势高度资料做参考。

图4和图5分别为ECMWF高空纬向风和经向风预报垂直插值前后的剖面。从中可以看出,将等压面垂直插值到等位势高度面,纬向风速和经向风速剖面在插值前后的垂直结构和数值大小相差不大,二者非常接近。插值后纬向风的等位势面在500 gpm以下风速略小于对应等压面的风速,而在2 500 gpm以上125°～128°E附近的大值中心也稍微偏弱。以下本文都用线性插值方法作风场预报的垂直插值。

图4 预报期内华东地区ECMWF高空纬向风(单位:m/s)24 h预报的垂直插值前(a)、后(b)30°N垂直剖面Fig.4 Cross-section of ECMWF zonal wind forecasts (units:m/s) for 24 hours over East China,(a) before and (b) after vertical interpolation during the forecast period

图5 预报期内华东地区ECMWF高空经向风(单位:m/s)24 h预报的垂直插值前(a)、后(b)30°N垂直剖面Fig.5 Cross-section of ECMWF meridional wind forecasts (units:m/s)for 24 hours over East China,(a) before and (b) after vertical interpolation during the forecast period

3 风场的多模式集成预报

本文中多模式集成预报选取滑动训练期,最优训练期长度通过试验获得。本文经试验,选取40 d作为最优训练期长度。此前消除偏差集合平均预报优于简单集合平均(Krishnamurti et al.,1999,2000,2003;Zhi et al.,2012)。下面着重对比GRAPES-GFS、ECMWF单模式预报、多模式消除偏差集合平均以及扩展复卡尔曼滤波方法(He et al.,2013)的预报效果。

图6显示,BREM、ACEKF风场多模式集成预报优于ECMWF、GRAPES-GFS单模式预报,ACEKF风场预报误差明显小于2个单模式预报以及BREM多模式集成预报。在预报期为第12天,也就是2020年3月4日模式预报误差比较大,由于有持续阴雨和大风预警,运用扩展复卡尔曼滤波多模式集成对预报进行处理后对预报的改善比较明显。

图6 预报期内华东区域平均10 m纬向风(a)、经向风(b)和全风速(c)单模式和多模式集成24 h预报的均方根误差(单位:m/s)Fig.6 Regional average RMSEs (units:m/s)of individual models and multimodel ensemble 24-hour wind forecasts over East China for (a) surface zonal wind,(b) meridional wind,and (c) full wind speed during the forecast period

为更好地考察华东地区几个重要机场的多模式精细化风场预报的性能,分别选取厦门(118.13°E,24.54°N)、上海(121.66°E,31.15°N)、青岛(120.37°E,36.26°N)3个机场的风场进行多模式集成预报试验。如图7所示,对比BREM、ACEKF方法及单模式ECMWF和GRAPES-GFS的风场预报效果,发现3个城市的纬向风、经向风以及全风速均方根误差随高度变化的趋势较为一致。ACEKF多模式集成预报均方根误差最小,BREM预报均方根误差也较2个单模式预报的均方根误差小。对厦门机场风速预报的改进效果要略优于上海、青岛机场。均方根误差在300～1 000 gpm时随高度增大而增大,ACEKF多模式集成预报的均方根误差较其他方案的增幅小,1 000～1 500 gpm高度层上均方根误差随高度增大而减小,1 500～3 000 gpm均方根误差有先增大再减小的趋势。ECMWF单模式预报在1 500～3 000 gpm均方根误差增大较明显。ACEKF多模式集成预报不但均方根误差较其他3种方案的预报均方根误差小,且随高度变化也不如单模式预报的大。总体来说,地面附近的风场预报误差略大于3 000 m高度上风场的预报误差,但高空1 800～2 400 m,风场的预报均方根误差较其他层次明显偏大。

图7 预报期内平均的厦门(a—c)、上海(d—f)和青岛(g—i)地面和高空风场预报的均方根误差(单位:m/s)的垂直分布:(a、d、g)纬向风;(b、e、h)经向风;(c、f、i)全风速Fig.7 (a,d,g) Vertical distribution of time-mean zonal wind,(b,e,h) meridional wind,and (c,f,i) full wind speed forecast RMSEs (units:m/s) over (a—c) Xiamen,(d—f) Shanghai,and (g—i) Qingdao airports during the forecast period

4 结论与讨论

本文基于ECMWF、GRAPES-Meso、GRAPES-GFS、GFS四个中心的华东及周边地区2020年1—4月的风场预报资料,对比4种水平插值方法,选取最优插值方法来获得水平方向上风场的降尺度预报。在垂直方向上,将等压面上风场预报插值到每隔300 m的等位势高度面上。为进一步提高风场预报的准确率,利用去除偏差集合平均(BREM)和扩展复卡尔曼滤波(ACEKF)2种方案对地面和高空风预报进行多模式集成预报试验,最终获得满足站点终端管制区飞行气象保障的三维空间的精细化风场预报。得到如下结论:

1)对于华东地区地面和高空风场预报的水平插值,反距离加权插值方法的均方根误差最小,而三次样条插值方法的均方根误差最大。经向风也有类似的特征,即反距离加权插值方法的均方根误差最小,而三次样条插值方法的均方根误差最大。此外,纬向风预报的插值均方根误差较经向风的更小。

2)BREM、ACEKF地面风场多模式集成预报优于ECMWF、GRAPES-GFS单模式预报,无论是地面还是高空ACEKF风场预报均方根误差明显小于2个单模式预报以及BREM多模式集成预报的均方根误差。

3)对华东地区上海、青岛和厦门3个机场地面和高空风的多模式集成风场精细化预报的分析表明,ACEKF多模式集成预报的均方根误差,远远小于BREM多模式集成预报和单模式预报的均方根误差。此外,ACEKF多模式集成预报不但均方根误差较BREM、ECMWF和GRAPES-GFS的预报均方根误差小,且随高度变化也不如单模式预报的大,其预报性能更为稳定。