基于多源证据估算气候敏感度最新研究进展:IPCC AR6解读

赵树云,袁畅,张华,周喜讯,刘梦婷,王海波,何静怡,于晓超

① 中国地质大学(武汉) 环境学院 大气科学系,湖北 武汉 430078;

② 中国气象科学研究院 灾害天气国家重点实验室,北京 100081;

③ 中国气象局 上海台风研究所 区域数值预报研究室,上海 200030

地球气候系统维持在某个状态主要是与当时的能量收支情况相适应。如果地球能量收支发生变化,比如自然和/或人类活动造成了辐射强迫,那么地球气候系统的状态也会发生变化,以便重新恢复能量收支平衡。这个过程里,有一个对应关系是我们特别需要关注的,那就是一定量的辐射强迫对应多大幅度的气候状态变化(常用地表温度变化代表),这个定量的对应关系正是气候敏感度要表征的。

IPCC AR6第一工作组报告第七章(Forster et al.,2021)评估了两个气候敏感度相关量:平衡态气候敏感度(Equilirum Climate Sensitivity,简称ECS)和瞬态气候响应(Transient Climate Response,简称TCR)。ECS的定义为大气中CO2浓度突然增加到工业革命前(1750年的278 ppm,1 ppm=10-6,即体积分数为278×10-6)的两倍(以下简称abrupt2×CO2)并一直维持,当气候达到新的平衡态时,全球平均地表温度相对工业革命前的变化。虽然由abrupt2×CO2数值试验得出,但ECS反映的是气候系统内在的性质。在一定的温室气体排放增加的路径下,敏感度越高的气候模式预测的未来增暖也越强。TCR的定义为大气中CO2浓度从工业革命前开始以每年1%速度增加(即CMIP6中的1pctCO2试验),当CO2浓度增加到工业革命前的两倍时(大约在第70年),全球地表温度相对工业革命前的变化。同ECS一样,TCR反映的也是气候系统的内在属性。

对比ECS与TCR,不难看出二者的区别:1)对于ECS,强迫是一次性引入的,且引入之后一直保持不变,而对于TCR,强迫是以1%的比例逐年增加的(图1);2)ECS要求气候系统重新恢复能量收支平衡,而TCR以CO2浓度增加到工业革命前的2倍为时间节点,不要求气候系统恢复能量收支平衡。因为TCR不要求气候系统恢复到能量收支平衡,所以它的模拟结果受海洋热吸收的影响,而且也正因海洋热吸收的缓冲,TCR的结果总是小于ECS(Hansen et al.,1985;Knutti,2005;Millar et al.,2015;Flynn and Mauritsen,2020;Tsutsui,2020)。ECS和TCR可以让我们从不同方面理解气候系统对外强迫的响应过程。

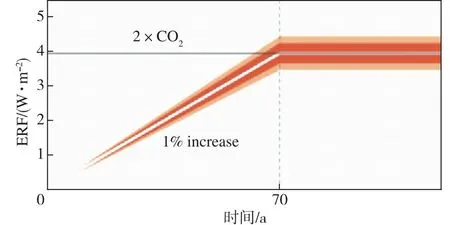
图1 abrupt2×CO2试验(灰色实线)和1pctCO2试验(带阴影白色实线)对应的有效辐射强迫(单位:W·m-2)随年份的变化(引自IPCC AR6 WGI第七章图7.17)Fig.1 Time evolution of the effective radiative forcing (units:W·m-2) to abrupt 2×CO2experiments (solid gray lines) and 1pctCO2 experiments (solid white lines with shading).The original figure is from IPCC AR6 WGI Chapter 7 Figure 7.17

针对IPCC AR6,已有不少解读文章发表(姜大膀和王晓欣,2021;廖宏和谢佩芙,2021;孙颖,2021;张华等,2021,2022;赵树云等,2021;周波涛,2021),其中张华等(2021,2022)和赵树云等(2021)从不同角度对第七章内容进行了解读。AR6第七章中的一个重要内容是基于多源证据对ECS和TCR的评估,而之前的解读文章尚未深入解读该部分。在AR6之前,对ECS和TCR的估计主要依赖气候模式模拟。所谓“孤证不立”,AR6对ECS和TCR的评估来源于多条证据线。本文将针对基于多源证据对ECS和TCR的评估进行解读,以便读者不仅了解ECS和TCR的综合评估结果,也了解支持该结果的证据。值得一提的是,AR6对ECS和TCR的最优估计中没有给地球系统模式的直接计算结果分配权重。不过,这并不是说地球系统模式的作用不再重要,实际上它在多条证据线中都发挥了重要作用,不再为其直接计算结果分配权重只是为了避免重复考虑。IPCC AR6对地球系统模式的作用也进行了梳理,本文中也简单做一解读。

1 AR6中对于ECS和TCR评估的多条证据线

1.1 过程理解

1.1.1 ECS

基于过程理解估算ECS的出发点是辐射强迫-气候响应的能量框架,根据这个框架有以下关系(Gregory et al.,2002):

ΔN=ΔF+αΔTs。

(1)

其中:ΔN代表全球年平均大气顶辐射能量失衡(单位:W·m-2),向下为正;ΔF代表辐射强迫(单位:W·m-2),从AR6开始采用有效辐射强迫(简称ERF)的概念(Sherwood et al.,2015);α代表气候反馈参数(单位:W·m-2·℃-1);ΔTs代表全球年平均地表温度变化(单位:℃),AR6中用全球平均地表气温变化代替。公式(1)中等号右侧两项分别代表外因对气候系统的强迫和气候系统对强迫的适应。

ECS定义在CO2浓度突然加倍并保持不变的情况下,我们用ERF2×CO2代替ΔF;并且要求气候系统重新恢复能量收支平衡,即ΔN=0。经过这样的替换,公式(1)中的ΔTs即为ECS:

ECS=-ERF2×CO2/α。

(2)

ERF2×CO2和α可以由决定它们的关键物理过程分别估计,特别地,ERF2×CO2可以由2×CO2的瞬时辐射强迫加快速调整获得,而2×CO2的瞬时辐射强迫可以由逐线积分精确计算。对α的估算要复杂一些,需要综合地球系统模式模拟、理论推导、观测分析和高分辨率的过程模拟来进行(Forster et al.,2021;赵树云等,2021)。

IPCC AR6对ERF2×CO2的估计值为3.93±0.47 W·m-2,而α的估计值为-1.16±0.40 W·m-2·℃-1,后面的范围均为1倍标准差。假设ERF2×CO2和α满足独立正态分布,ECS的估计值和不确定范围可由二者的概率密度分布估算。如此,估算的ECS最优值为3.4 ℃,可能区间(17%～83%)为2.5～5.1 ℃,非常可能区间(5%～95%)是2.1～7.7 ℃。因为α是个小值,又在分母上,它对ECS不确定性的贡献是ERF2×CO2的三倍,并且受其影响,ECS的概率密度分布曲线向右侧有个拖尾。

不过,假设ERF2×CO2和α互相独立是否合理呢?在CMIP5和CMIP6多模式中,利用abrupt4×CO2试验(大气中CO2浓度突然增加到工业革命前的四倍)和回归法计算二者,发现它们有负相关关系(r2=0.34)(Andrews et al.,2012;Webb and Gregory,2013;Zelinka et al.,2020),这会导致二者模式间离散度有相互抵消的情况,从而缩小ECS的不确定范围。用固定海温的大气环流模型和固定CO2浓度的海-气耦合模型分别计算ERF2×CO2和α,也发现二者存在负相关(Ringer et al.,2014;Chung and Soden,2018)。一种解释是热带海洋上低云的调整(ERF2×CO2的分量)和反馈(α的分量)之间存在负相关关系(Ringer et al.,2014;Chung and Soden,2018)。不过,ERF2×CO2和α之间负相关背后确切的物理机制现在尚不明确,而模式中对控制低云的物理过程描述还很不完善。基于这种情况,AR6仍采用ERF2×CO2和α相互独立的假设。

1.1.2 TCR

基于过程理解的思路也可推广至对TCR的估计,只是这个过程需要用到一个两层能量收支模拟器。模拟器中的第一层代表大气、陆地和浅层海洋,第二层代表深层海洋。根据Geoffroy et al.(2013a),它们的能量收支用数学公式表达如下:

(3)

(4)

其中:C和Cd分别为两层的有效热容(单位:W·m-2·a·℃-1);ΔT和ΔTd分别代表两层的温度变化(单位:℃);ERF为随时间变化的有效辐射强迫(单位:W·m-2);α为气候反馈参数(单位:W·m-2·℃-1);γ为两层之间热传递系数(单位:W·m-2·℃-1);ε被称为效能参数,是一个无因次系数,代表海洋热吸收对海表温度分布模态演变的依赖。

假设引入一个外强迫ERF,气候能瞬间恢复收支平衡,那么温度变化为-ERF/α,称之为瞬时平衡温度,记作ΔTeq,并用它代替公式(3)中的ERF。然后,在公式(4)等号两侧各乘系数ε,如此两层能量收支模拟器可写成下面形式:

(5)

(6)

其中:Cd′=εCd;κ=εγ。公式(5)与(6)可以写成矩阵形式:

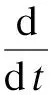
(7)

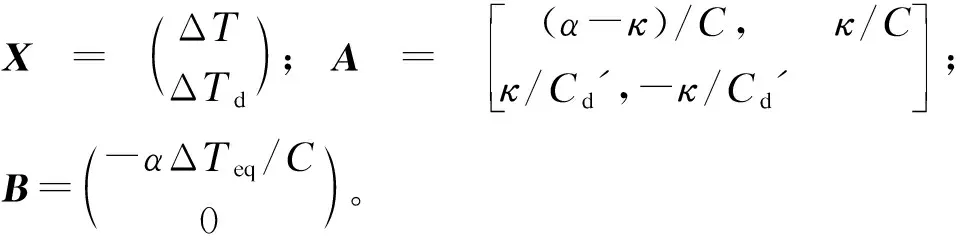
(8)

由公式(8)可以看出,因为TCR不要求气候恢复平衡,它将在ECS上面增加两个修正项(方括号中),一项与快速调整有关,一项与气候慢响应有关。τf和τs分别为快速调整和慢响应的衰减时间尺度。公式(8)中的τf、τs、af、as的值可由公式(5)和(6)中的系数C、Cd、γ、ε、α计算出来。Geoffroy et al.(2013a,b)利用CMIP模式的abrupt4×CO2试验校准过(3)—(8)式中的参数,它们分别为:

C=8.1±1.0 W·m-2·a·℃-1,

Cd=110±63 W·m-2·a·℃-1,

γ=0.62±0.13 W·m-2·℃-1,

ε=1.34±0.41,

κ=0.84±0.38 W·m-2·℃-1,

τf=4.6 a,

τs=33 a,

af=0.541,

as=0.459。

以上数值见IPCC AR6第一工作组报告第7章附录7.SM.2(Forster et al.,2021)。

Jiménez-de-la-Cuesta and Mauritsen(2019)的研究认为,TCR的形式可以写得更简单一些:

TCR=ERF2×CO2/(-α+κ)。

(9)

其中:ERF2×CO2/(-α)即为ECS,(8)式中对ECS的复杂修正综合在一个气候反馈参数修正项κ中。κ是海洋热吸收系数γ和代表海温模态效应(全球平均海温相同的情况下,因海温空间模态不同而对气候反馈参数产生的影响(张华等,2022))的无因次系数ε的点积,代表了海洋热吸收对全球气候增暖的缓冲作用。因κ>0,所以TCR一定是小于ECS的。将基于过程理解的ECS代入公式(8)可以算出1至70 a的ΔT,第70年的ΔT即TCR。当模拟器中的参数都设置为CMIP6多模式结果的平均,那么TCR的不确定范围可以由ECS的范围计算。实际的TCR受海洋热吸收效率γ和效能参数ε的影响。当用CMIP5模式的瞬态响应来校准模拟器时,发现海洋热容(Cd)的不确定性可以忽略,γ和ε的不确定性解释了TCR在不同模式中误差的10%～20%(Geoffroy et al.,2012)。实际的海洋热吸收受多个平流和混合过程控制,但在模拟器中简化为了一个表层和深层海洋之间的热交换系数。因此,基于过程理解约束γ和ε是一项挑战。因为模式之间对于κ的评估值一致性很弱,在忽略协方差的情况下,κ的平均值和一倍标准差为κ=0.84±0.38 W·m-2·℃-1,在考虑这个κ的模式间离散度之后,TCR的不确定范围扩大了10%。尽管如此,TCR不确定性的主要贡献依然是净反馈参数α(Williams et al.,2020),与CMIP6模式结果一致,海洋热吸收κ不确定性的贡献是次要的。IPCC AR6基于过程理解估算的TCR的中值为2.0 ℃,可能区间为1.6～2.7 ℃,非常可能区间是1.3～3.1 ℃。

1.2 仪器记录

1.2.1 基于全球能量收支

IPCC AR6估计2006—2019年全球地表平均气温相比于1850—1900年增加了1.03[0.86～1.18] ℃(以下如未特别说明,方括号内为5%～95%置信区间)。结合地球能量收支不平衡和ERF,可以用该温度变化来估算ECS和TCR,即联立公式(1)和公式(2),可以得到:

ECS=ERF2×CO2ΔTs/(ERF-ΔN)。

(10)

其中:ERF2×CO2代表2×CO2的有效辐射强迫;ΔTs和ERF代表历史上地表温度变化和有效辐射强迫;ΔN代表地球能量收支失衡。TCR可以写成以下形式:

TCR=ERF2×CO2ΔTs/ERF。

(11)

不过,公式(11)需假设辐射强迫的增加可以足够快以至于深层海洋未来得及调整,又足够慢以使表层海洋充分调整,这样ΔT和ΔN与ERF大约成比例增加。由于ΔN是正值,因此TCR总是小于ECS,同时因为分母里少一个量ΔN,所以TCR比ECS更易约束。由于分母中ERF的不确定性,从历史变暖中估算出的TCR和ECS的上界比下界不确定性更大。需要注意的是,这条证据并不单纯基于观测。事实上,地球系统模式模拟可以为历史上的ERF和1850—1900年地球能量收支不平衡提供部分信息,还可用于估计历史上内部变率对温度和能量不平衡变化不确定性的贡献。

基于全球能量收支估算ECS需要考虑地表增温的空间模态对辐射反馈的影响,但传统能量收支框架没有考虑这一点,而是假设净辐射反馈参数α是个定值,这样估算出的是有效ECS,并非真实ECS。有多条证据表明α会因未来增暖空间模态的演变而向正值方向移动,从而导致ECS增加,比如Winton et al.(2020)利用CMIP6中的GFDL-CM4.0模式,从历史试验的能量收支中得到有效ECS为1.8 ℃,而用abrupt4×CO2试验中得到的ECS为5.0 ℃;Andrews et al.(2019)利用HadGEM3-GC3.1-LL模式得到的相应结果分别为4.1 ℃和5.5 ℃。为了将空间模态效应考虑进来,2013年以来的许多研究对传统能量收支框架进行了扩展,允许在不同时间尺度上采用不同辐射反馈参数(Armour et al.,2013;Geoffroy et al.,2013a;Armour,2017;Proistosescu and Huybers,2017;Goodwin,2018;Rohrschneider et al.,2019),这样辐射反馈会随着气候变化的空间模态或海洋热吸收幅度的变化而变化,或者随辐射强迫类型的不同而变化。在公式(2)上增加一个修正项,可写成以下形式:

ECS=ERF2×CO2/(-α+α′)。

(12)

其中:α′表示历史时期和CO2强迫下平衡态气候反馈参数之间的差值,基于多个证据AR6对其估计值在0～1.0 W·m-2·℃-1范围内,用α′=0.5±0.5 W·m-2·℃-1代表。从历史气候变暖中估算的有效ECS为2.5[1.6～4.8] ℃,考虑该α′后可修正为3.5[1.7～13.8] ℃。Andrews et al.(2019)利用HadGEM3-G3.1-LL在历史强迫下得到的α′为0.1±0.3 W·m-2·℃-1,对应的ECS为2.7[1.7～5.9] ℃。在这两种情况下,ECS范围的下界与传统能量收支框架(即α′=0)推算的有效ECS接近,说明ECS较小时对α′的依赖性较弱,而ECS范围的上界远大于有效ECS的上界,并且强烈依赖于α′的值。

许多文献表明,2007年之前全球能量收支在估算TCR和ECS中的约束作用还很弱,给出的有效ECS的值经常超过10 ℃(Forster,2016;Knutti et al.,2017),主要因为对流层气溶胶强迫有很大的不确定性。2013年IPCC AR5修正了气溶胶有效辐射强迫,减小了其负辐射强迫,同时增大了温室气体正辐射强迫,二者共同结果使ERF的估计值更大。在计算TCR和ECS时(ERF在分母上),由于ERF的增加使TCR和ECS的不确定范围缩小,主要是上界缩小,比如,Otto et al.(2013)基于更新至2009年的全球能量收支和辐射强迫对TCR和有效ECS进行评估,二者分别为1.3[0.9～2.0] ℃和2.0[1.2～3.9] ℃。

当前,科学界基于能量收支估算TCR和ECS有了几点提高。比如,采用了更准确的全球地表温度观测数据,对截至2020年的温度趋势有了更深的认识;修正了对地球能量不平衡和ERF的估计。IPCC AR6使用全球地表气温数据估算温度趋势,尽管不确定性很大,但全球平均地表气温趋势与观测的全球平均地表温度趋势有相同的最佳估计值。选择全球地表气温估算全球地表温度趋势,可以使得基于能量收支估计的ECS和TCR与其他证据之间进行相互比较。基于全球自动浮标观测估算的2006—2019年间地球能量收支失衡的估计值约为0.79±0.27 W·m-2。而包括地球系统模式模拟、能量平衡模拟、海洋模式模拟解析及利用惰性气体测温法重建的海洋变暖等多条证据表明,1850—1900年地球能量收支失衡为0.2±0.2 W·m-2(Lewis and Curry,2015;Armour,2017;Baggenstos et al.,2019;Gebbie and Huybers,2019;Zanna et al.,2019)。结合对地球能量失衡内部变率的估计,2006—2019年相比1850—1900年的能量失衡异常ΔN估计值为0.59±0.35 W·m-2(Palmer,2017;Sherwood et al.,2020)。考虑温度内部变率后,2006—2019年相比1850—1900年的全球地表气温变化ΔT估计值为1.03±0.2 ℃(Sherwood et al.,2020),ERF估计值为2.20[1.53～2.91] W·m-2,CO2浓度加倍的估计值为3.93±0.47 W·m-2。将这些值代入公式(10)和(11)中,可得到TCR和有效ECS估计值分别为1.9[1.3～2.7] ℃和2.5[1.6～4.8] ℃。

1.2.2 基于气候模式仿真器

能量收支模拟器相比综合的地球系统模式要简单很多。比如,一个模拟器可以用若干相连的方框来分别表示大气、海洋和陆地(Goodwin,2016),或者用两个相连的海洋层来表示全球平均气候。不过,由于降低了复杂性,模拟器缺乏对海表温度空间模态的刻画,也就无法反映当海温空间模态变化后的辐射响应,因此使用模拟器获得的ECS范围为历史记录时期的有效ECS,而非真正的ECS。

能量收支模拟器的计算效率很高,这意味着可以用观测结果对它进行经验约束。可以从先验分布中随机抽取参数(例如,气候反馈参数、气溶胶辐射强迫、海洋扩散系数等)的大量可能值,把这些参数值代入模型并向前积分,根据地表或海洋变暖的观测结果进行权衡,从而获得目标量(如TCR、ECS和气溶胶强迫)的后验估计。近十年基于能量收支模拟器的研究总体上估算的有效ECS在1～5 ℃,TCR在0.9～2.6 ℃,二者中值总体落在了基于历史全球能量收支估算结果的5%～95%范围内。但当考虑到未来全球变暖空间模态演变而导致的辐射反馈变化时,它们估计的ECS值将会更高。先前研究用模拟器估算的有效ECS值多位于基于历史全球能量收支的估计范围的下端(Padilla et al.,2011;Schwartz,2012,2018;Johansson et al.,2015;Goodwin,2016;Skeie et al.,2018),原因可能是基于全球能量收支中使用了最新的地球能量不平衡、全球地表气温变化趋势和ERF,而不是两条证据线之间方法上的差别。

1.2.3 基于卫星观测的大气顶辐射收支变化

虽然对大气顶辐射通量的连续卫星观测无法足够精确地给出地球能量不平衡的大小,但对其2002年后的变化趋势的估计是准确的(Loeb et al.,2012;Johnson et al.,2016;Palmer,2017)。卫星观测的大气顶辐射量可以结合全球地表温度观测和简单的全球能量平衡模型估计与近期气候变化相应的净反馈参数,进而利用回归法估算ECS。

2013年以来的研究指出,用回归方法得到的反馈参数依赖于使用年平均还是月平均结果,以及回归时对滞后时间的选择,这使该方法使用起来较复杂(Forster,2016)。从卫星观测中得到的全球大气顶辐射与全球地表温度之间的超前滞后关系及其对采样周期的依赖性,在没有强迫下的地球系统模式模拟中可以很好地再现。从这个意义上讲,回归方法更适于估算与内部气候变率相关的辐射反馈(Brown et al.,2014),而非直接估算ECS。利用数值模式寻找大气顶辐射和地表温度之间的关系需要几百年的模拟时间,这从侧面说明卫星观测的时间长度可能不足以得到可靠的反馈估计。不过,当关注特定过程或区域时,回归法计算的短期反馈和长期反馈之间的相关性高于全球平均,例如云或水汽反馈(Dessler,2013;Zhou et al.,2015)。

1.2.4 基于火山喷发的气候响应

一些研究使用20世纪观测到的火山喷发引起的气候响应估算ECS(Knutti et al.,2017)。然而,火山喷发对于ECS的直接约束作用是很弱的,特别是对ECS的上界,这是由于温度对短期强迫的响应与辐射反馈的关系很弱(Geoffroy et al.,2013b;Merlis et al.,2014),并且火山喷发期间大气顶的辐射收支变化里面有很大一部分由快速调整贡献。另外,将火山喷发的响应与随后几年的内部气候变率区分开来也是一项挑战(Wigley et al.,2005)。有基于地球系统模式模拟的研究发现,全球地表温度对火山喷发响应过程中的辐射反馈与长期全球变暖中的辐射反馈可以差别很大(Merlis et al.,2014;Marvel et al.,2016;Ceppi and Gregory,2019)。因此,利用火山喷发引起的气候响应直接估计ECS或气候反馈是较困难的,但是它们可以用在对ECS的萌现约束中(也有称涌现约束(张华等,2021,2022;周佰铨和翟盘茂,2021))。

1.3 古气候数据

使用古气候数据对ECS进行估算的优势包括:1)它基于真实地球系统对强迫响应的观测,而非基于模式直接或间接估算;2)与仪器记录的数据相比,古气候数据中的强迫相对较大(在量级上类似于2×CO2或更多);3)强迫的变化相对缓慢,因而气候系统接近平衡,这样就可以包含所有的反馈过程;4)海洋热吸收的处理也比仪器记录数据简化很多。然而,对古强迫和古全球地表温度响应的估算可能存在相对较大的不确定性,而且必须考虑冰盖的长期反馈,但AR6的ECS定义中并没有考虑这种反馈,这与其他证据线是不一致的。此外,反馈对气候状态的依赖性意味着地球古气候时期的气候敏感度可能与现在不同。

导致末次盛冰期(距今约2.4～1.8万年)寒冷气候的主要强迫和反馈过程包括CO2、非CO2温室气体和冰盖变化等,轨道参数造成的强迫相对于工业革命前可忽略不计。总的来说,末次盛冰期的全球平均温度比工业革命前低5～7 ℃。通常假设末次盛冰期气候是完全适应强迫的(即ΔN=0),并在只有CO2强迫的情况下,假设末次盛冰期冰盖经过充分反馈达到平衡状态,这样计算出的是地球系统敏感度(Earth System Sensitivity,ESS),而不是ECS,ESS比ECS多考虑了冰盖的长期反馈。为了计算ECS,Rohling et al.(2012)在公式(10)中引入了一个额外的强迫项,即将冰盖的辐射反馈(主要是通过地表反照率变化)等效成一个强迫项,此项通常用地球系统模式来模拟,这会给ECS的估计造成额外的不确定性。表1汇总的ECS结果已经考虑了对冰盖长期反馈的处理,其ECS物理内涵与其他证据线是一致的。

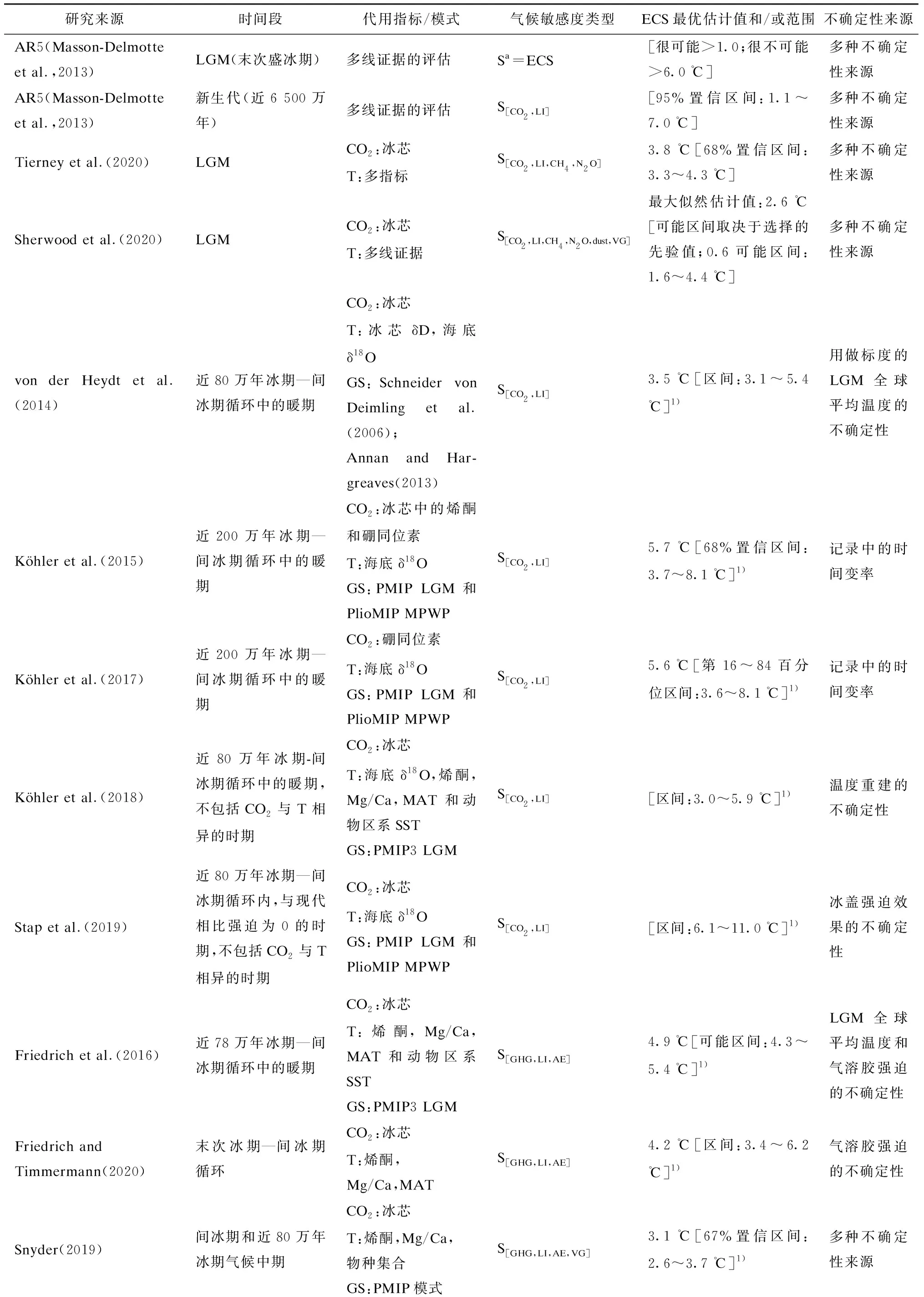
表1 基于古气候数据对ECS估算的汇总(原表为IPCC AR6 WGI第七章表7.11)

2013年以来,一些研究将Rohling et al.(2012)的方法推广到了冰期-间冰期(距今约200～100万年)循环中(表1)。与末次盛冰期相比,从冰期-间冰期循环中计算的ECS不确定性总体偏大,原因有几点:1)全球地表温度代用资料的站点较少;2)缺乏详细的冰盖重建资料;3)对于有冰芯记录前的时期,CO2重建资料中的不确定性较大;4)在传统的全球平均强迫和响应的能量收支框架中考虑轨道变化所带来的强迫具有挑战性(Schmidt et al.,2017),即便其全球年平均值接近零,其强迫的季节和南北分布可以直接影响全球年均地表温度(Schmidt et al.,2017)、冰量(Abe-Ouchi et al.,2013)和一些反馈过程(如与甲烷有关的过程)(Singarayer et al.,2011);5)间冰期的强迫和温度响应都是接近零的小值,这造成所估算的ECS具有相对较大的不确定性。所有基于冰期-间冰期循环的研究均只考虑更新世的暖期,主要是它的气候平均态与现代相似,可以尽量减小气候平均态对气候反馈的影响。

在前第四纪暖期(距今约250万年以前),强迫与响应的正负和大小总体与预估的未来气候变化相似(Burke et al.,2018;Tierney et al.,2020)。基于前第四纪暖期估算ECS时存在的不确定性与基于末次盛冰期时的相似,但主要的不确定性与强迫有关。因为在有冰芯记录之前,CO2浓度只能间接估算。然而,2013年以来关于有冰芯记录前CO2浓度重建的研究取得了进展,前第四纪暖期CO2浓度的不确定性有所减小,使得这一时期可以用于评估气候敏感度(表1)。

中上新世暖期(距今约330～300万年)的相关资料具有一定优势,已被一些研究用于ECS的约束研究(Martínez-Botí et al.,2015;Sherwood et al.,2020)。首先,中上新世暖期的CO2浓度相对较高(350～425 ppm),而且当时的地形条件和大陆结构与现代相似,该时期可能是与当下最为相近的自然地质时期参照。除此之外,中上新世暖期的全球地表温度处在一个适中范围,反馈的非线性变化不明显。在中上新世暖期中,KM5c间冰期(中心在距今320.5万年)时的地球轨道与现代非常相似(Haywood et al.,2013,2016)。这些优势对于评估ECS极其有用。

在早始新世(距今约5 600～4 800万年),尽管当时的气候变化信号整体较强,但强迫和温度变化的不确定性更大。由于当时的大陆形状、地形、海深与现代不同(Farnsworth et al.,2019),更长时间尺度的温度和CO2的测量结果通常不同步,且反馈对温度有较大的依赖性(Royer,2016),因此给估算ECS带来了挑战。

表1总结了从古气候数据中直接约束ECS的结果。尽管一些结果并非独立的,比如von der Heydt et al.(2014)、Köhler et al.(2015,2017)和Stap et al.(2019)用到了相似的代用记录,但仍有多个来自不同时期的独立证据线,包括末次盛冰期(Sherwood et al.,2020;Tierney et al.,2020)、冰期—间冰期(Royer,2016;Köhler et al.,2017;Snyder,2019;Friedrich and Timmermann,2020)、上新世(Martínez-Botí et al.,2015;Sherwood et al.,2020)和始新世(Anagnostou et al.,2016,2020;Shaffer et al.,2016;Inglis et al.,2020)。它们用到不同的代用记录估算强迫(例如,冰芯中的CO2和硼同位素)与响应(例如,δ18O、Mg/Ca等)。表中第四列,Sa表示根据Rohling et al.(2012)的气候敏感度分类。许多研究估计ECS时仅考虑CO2和冰盖反馈造成的强迫,这种处理相当于Rohling et al.(2012)中的气候敏感度类型S[CO2,LI],也与IPCC AR6和本文中ECS定义一致。一些研究也考虑了其他类型的气候敏感度类型(第四列)。不同研究关注的时段不同,采用的古气候代用指标和模式也不同。第六列说明了不确定性来源。由表1可知,从古气候数据中估算的ECS范围的下限均高于1.6 ℃。整体上,基于冰期-间冰期暖状态的研究给出的ECS估算值最大。考虑到对这些间冰期内冰盖强迫大小的估计存在很大不确定性,以及其他不确定性尤其是轨道强迫对ECS的直接影响,基于冰期-间冰期循环的研究给出的ECS的评估结果可信度较低。基于古气候数据估算ECS的重点是末次盛冰期和前第四纪暖期,通过这两个时段得到ECS的中间估计为3.4 ℃。基于古气候数据估算的ECS上边界的不确定性相对大于下边界。基于前第四纪暖期估算的ECS上边界平均为4.9 ℃,而末次盛冰期相应值则为4.4 ℃;考虑到基于这两个时期的估算是彼此独立的,同时考虑气候状态对ECS的影响以及其他不确定性,基于古气候记录估算的ECS上界很可能为4.5 ℃。

IPCC AR5基于对末次盛冰期的数据分析和模拟认为ECS不太可能位于1～6 ℃范围以外(Masson-Delmotte et al.,2013),并根据过去6 500万年的气候记录给出ECS的95%置信区间为1.1～7.0 ℃。IPCC AR6基于古气候证据对ECS的约束比IPCC AR5有所改进,对其理解也更为深入。一部分原因是现在研究使用了多个冰期-间冰期循环的高分辨率古气候数据,同时考虑了ECS对气候状态的依赖性,而且对前冰芯时期大气CO2浓度和地表温度的估计有了更好的约束。

1.4 萌现约束

地球系统模式的ECS和TCR存在较大的模式间方差,为了减小对它们估算的不确定性,可建立它们与其他可观测变量的萌现约束关系,然后结合气候变量的观测结果对ECS或TCR的概率分布进行约束。其中,萌现约束关系的建立依赖多模式集合。由此可见,能够进行萌现约束研究也受益于国际上对CMIP和其他多模式集合的协调工作。建立ECS或TCR和可观测变量的萌现约束关系时需要注意几点:1)需要有物理机制和理论基础,否则多模式集合中数千个通过显著性检验的统计关系会使人无从下手;2)多模式对可观测变量的模拟不能有系统性偏差;3)当萌现约束关系是非线性的情况下,需要合理考虑萌现约束关系的不确定性。

1.4.1 ECS

利用古气候时期温度变化对ECS进行约束有一定的优势,因为这些时期的气候是达到平衡态或接近平衡态的。缺点在于这些时期的温度和强迫数据用的都是代用指标,本身存在不确定性;另外,古气候时期的海温空间分布与模拟结果可能存在差异,会引入模态效应带来的不确定性;再有,参与古气候模拟的模式数量不够,也会影响约束关系的稳定性。当前,应用于萌现约束的古气候时期主要是末次盛冰期(Hargreaves et al.,2012;Hopcroft and Valdes,2015)和中上新世暖期(Renoult et al.,2020)。Hopcroft and Valdes(2015)与Hargreaves et al.(2012)的工作均是基于末次盛冰期,但是用到的模式不同,他们发现的约束关系并不完全一致,这说明萌现约束关系受所用模式集合的影响。Renoult et al.(2020)发现末次盛冰期和上新世的ECS 95%分位数均低于6 ℃,两个时期联合后的95%分位数下降到4.0 ℃。

利用器测记录的全球变暖约束ECS的优点是数据较准确,缺点是气候未达到平衡态,因此利用该时段进行萌现约束的一个假设是一般地球系统模式可以准确刻画短期与长期全球变暖的比率。因为气溶胶强冷却效应的干扰,1850年以来的变暖和ECS之间的相关性并不好。不过20世纪70年代后全球平均气溶胶有效辐射强迫的增加速率开始降低。一系列研究基于1970年以后的短期全球变暖对ECS进行约束,得到的最优值最小为2.0 ℃,最大为2.83[1.72～4.12] ℃(Bengtsson and Schwartz,2013;Jiménez-de-la-Cuesta and Mauritsen,2019;Nijsse et al.,2020)。Bender et al.(2010)利用1991年皮纳图博火山喷发引起的气候响应进行萌现约束,给出的ECS最佳估计值为2.4 ℃,可能区间为[1.7～4.1] ℃;把ENSO变化考虑进去,得出的最佳估计值为2.7 ℃。通过波动-耗散定理将全球地表温度短期变化中存在的滞后相关性与ECS联系起来,得到一个相当小的ECS,仅为1.1 ℃(Schwartz,2007)。Cox et al.(2018)使用CMIP5气候模式历史试验中全球地表温度的短期变化作为萌现约束,估算的ECS为2.8[1.6～4.0] ℃。基于CMIP6历史试验得出了偏高的ECS,为3.7[2.6～4.8] ℃(Schlund et al.,2020)。利用热带对流层温度变化引起的大气顶能量收支的短期变化对ECS进行萌现约束,得到的结果为3.3[2.4～4.5] ℃(Dessler and Forster,2018)。

还有研究利用云反馈和当前气候的模拟偏差进行ECS的萌现约束。由于CMIP5和早期气候模式集合中的气候敏感度的不确定性大多来自低云反馈,所以利用热带低云进行萌现约束得到了较广泛的应用,估算的ECS中值介于3.5～4 ℃,低于3 ℃的可能性较低(Volodin,2008;Sherwood et al.,2014;Zhai et al.,2015;Brient and Schneider,2016;Brient et al.,2016)。不过,该方法假设其他反馈过程都是无偏的,而这种假设存在缺陷,其结果勉强与其他萌现约束一致。而利用热带环流进行萌现约束得到的结果与其他萌现约束相矛盾。有研究利用代表当前全球温度变化或辐射收支模拟偏差的空间(季节)变化的某种指数与模式模拟的ECS进行关联,总体上给出了3.3～3.7 ℃的ECS最佳估计值(Covey et al.,2000;Knutti et al.,2006;Huber et al.,2011;Bender et al.,2012;Brown and Caldeira,2017;Siler et al.,2018)。然而,当前气候的模拟偏差与长期气候变化反馈之间的物理相关性尚不清楚,因此,利用模拟偏差对ECS的萌现约束的可靠性还不高。

总的来看,ECS的萌现约束研究可以分为两类:1)基于全球或近似全球指数,例如全球地表温度和大气顶能量收支;2)基于物理过程,比如模式对低云反馈或当前气候的模拟偏差。理论上,第一类比第二类更适合对ECS进行约束,后者与其说对ECS进行约束,不如说是对单个反馈进行约束。AR6综合考虑两类萌现约束结果,并考虑不同研究之间的依赖性、萌现约束方法的不成熟后适当放大不确定范围,给出的ECS的可能范围为1.5～5 ℃。

1.4.2 TCR

同样的,也出现了针对TCR的萌现约束方法,主要基于器测温度记录。Gillett et al.(2012)利用最简单的形式将一个模式的气候响应回归到单个历史强迫,获得了一个窄的TCR极可能范围:1.3～1.8 ℃;后来使用了一组模式,范围扩大为0.9～2.3 ℃(Gillett et al.,2013)。Ribes et al.(2021)基于相关数据同化的方法并考虑了气候响应空间模态的不确定性,给的结果为1.33～2.36 ℃,但结果依赖于选择的是CMIP5还是CMIP6模式集合。另一项研究利用对皮纳图博火山喷发的气候响应得到的范围为0.8～2.3 ℃(Bender et al.,2010)。Jiménez-de-la-Cuesta and Mauritsen(2019)基于20世纪70年代后全球变暖的萌现约束(该时期气溶胶强迫变化的方差较小),得出了TCR的一个更窄范围,为1.67[1.17～2.16] ℃。Tokarska et al.(2020)和Nijsse et al.(2020)基于CMIP6模式给出了TCR的估算范围与Jiménez-de-la-Cuesta and Mauritsen(2019)的接近,只是下界略低,分别为1.60[0.90～2.27] ℃和1.68[1.0～2.3] ℃。基于这些结果,TCR的最佳估计值为1.7 ℃,极有可能范围为1.1～2.3 ℃。

2 地球气候系统模式在ECS与TCR估算中的作用

图2汇总了IPCC AR6中不同证据对ECS和TCR的估计结果,包括过程理解、仪器记录、古气候数据和萌现约束,以及考虑这些证据后给出的综合评估。综合以上证据,IPCC AR6给出了ECS的最优估计为3 ℃,可能区间为2.5～4.0 ℃,非常可能区间为2.0～5.0 ℃;给出了TCR的最优估计为1.8 ℃,可能区间为1.4～2.2 ℃,非常可能区间为1.2～2.4 ℃。从图2可以看出,CMIP6模式的结果没有被当成一条证据,而是在最后给出来,ECS和TCR的模式结果分别由Schlund et al.(2020)和Meehl et al.(2020)提供。这是第六次评估报告与之前评估报告的不同之处。这是不是说明地球气候系统模式不再重要了呢?

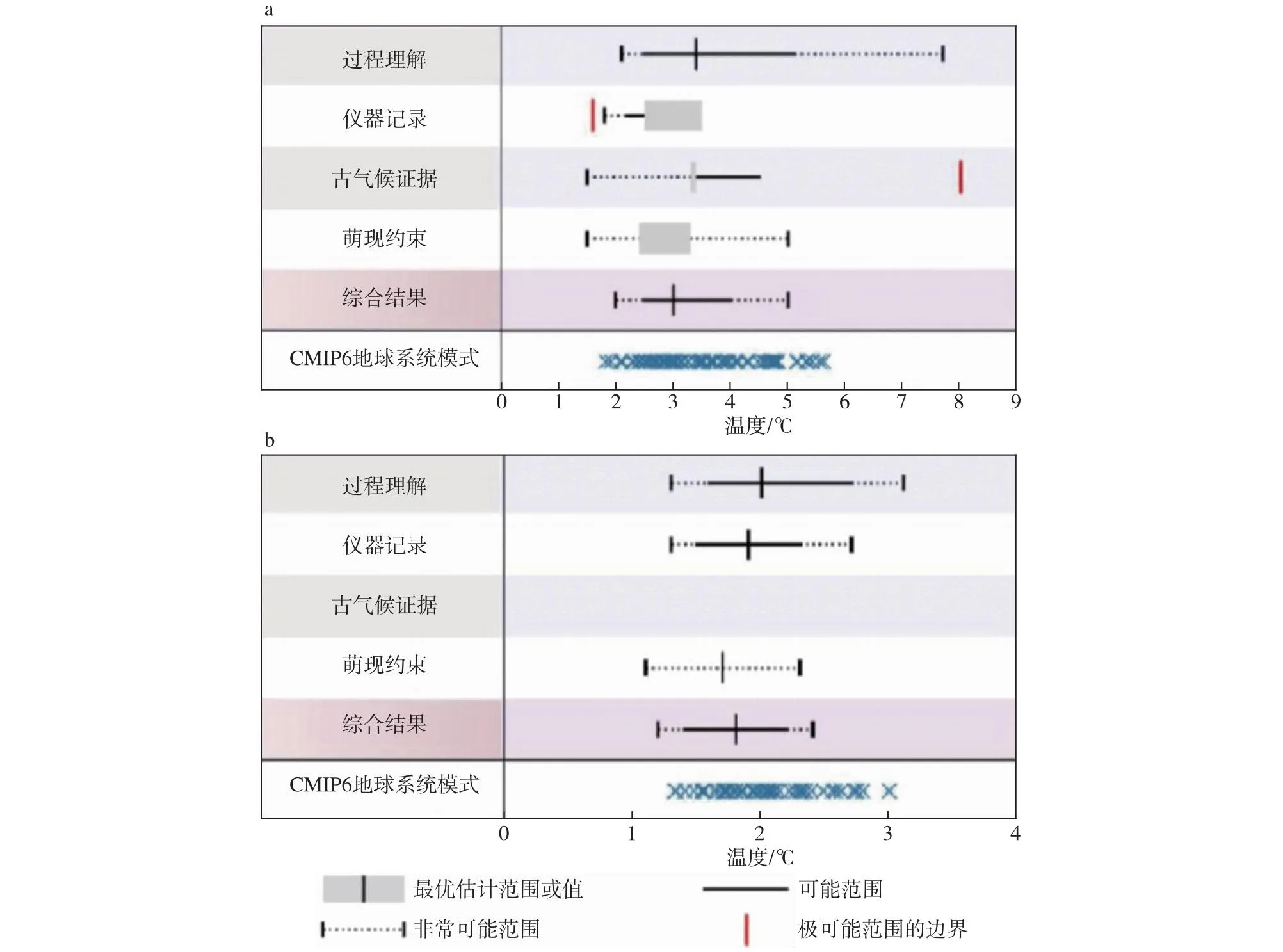
图2 不同证据对ECS(a)和TCR(b)估算的总结(引自IPCC AR6 WGI第七章图7.18)Fig.2 Summary of the (a)ECS and (b)TCR assessments using different lines of evidence.The original figure is from IPCC AR6 WGI Chapter 7 Figure 7.18

在IPCC第三次及之前的评估报告中,气候敏感度主要是由地球系统模式直接计算的。从AR4开始,历史变暖和古气候资料提供了额外的证据,并且指出仅用模式这个单一证据是有问题的。随着更多新证据的出现,AR6对各种数值模式的使用更为谨慎,除非认为它们是准确的、或者是唯一可用的信息源。但这不是说地球系统模式不重要。不用地球系统模式直接计算的ECS和TCR的主要原因是这些模式的信息已经在其他证据中被考虑了。例如,地球系统模式被部分用于估算历史和古气候强迫,将古气候的温度数据由局地转换为全球平均,估算反馈如何随SST空间模态变化,以及对ECS的萌现约束。另外,在理解温度、水汽、反照率、生物地球物理和非CO2生物地球化学反馈估算的过程中,地球系统模式也被用作重要证据。

AR6没有采用地球气候系统模式的直接结果,而是将它的作用融合在了其他多条证据中。这种处理有几点考虑:1)之前ECS的绝大部分模式间差异来自于云反馈,特别是低云。人们期待参数化的改进最终会导致模式响应的收敛,从而减小ECS的模式间差异。然而,经过几十年的模式发展、分辨率的提高和参数化方案的改进,ECS的模式估算并没有得到系统性的收敛。事实上,CMIP6得到的ECS的整体模式间差异还要大于CMIP5。2)通常很难确定一个地球系统模式中参数化的设计和发展考虑了哪些信息。气候模式经常共享一些模块代码,在某些情况下除了稍加修改甚至共享整个子模块。因此,不同模式之间不是独立的,很难对模式集合所提供的信息进行统计,也不能排除它们共有的局限性会导致模式集合出现系统偏差,这种系统偏差可能会反映在利用它们评估的ECS上。3)如何判断一个模式模拟的好坏是困难的,在长期的历史变暖中,低ECS和高ECS模式都能够模拟出与观测一致的变暖,部分原因可能是气溶胶冷却效应在其中起了补偿作用。

CMIP6中ECS的模式间差异相比CMIP5有所增加,而基于多条证据对ECS认识的加深反而缩小了ECS的不确定性区间,这样CMIP6集合包含了ECS综合评估的非常可能区间(2～5 ℃)。不在此区间的模式可以用于对ECS和TCR建立萌现约束,并为“尾部风险”提供实例,以便在动力上形成对未来气候变化一致的模拟,从而为影响研究和风险评估提供信息。

3 总结与展望

气候敏感度是影响未来气候变化的重要指标,当辐射强迫确定后,未来的气候变化很大程度上取决于气候敏感度的大小。IPCC AR6基于多源证据对平衡态气候敏感度ECS和瞬态气候响应TCR进行了评估,包括过程理解、仪器记录、古气候数据和萌现约束。多条证据线之间达成了广泛一致,支持ECS的中心估计值接近3 ℃,可能区间为2.5～4.0 ℃,非常可能区间为2.0～5.0 ℃。TCR的证据不如ECS充足,主要集中在器测温度记录、萌现约束和过程理解,给出TCR的最佳估值为1.8 ℃,可能区间为1.4～2.2 ℃,非常可能区间为1.2～2.4 ℃。

与之前的评估报告不同,AR6没有将模式结果当成一条独立的证据线,仅仅将CMIP6的结果给出来与其他证据线的综合评估结果进行了对比。总体上看,CMIP6直接计算的ECS和TCR平均值高于CMIP5和AR6基于多条证据的综合评估。不过,这不意味着地球气候系统模式不再重要,实际上它们被广泛应用于其他几条证据线,以便得到一个自洽的结果。不把它列为单独的证据线是为了避免重复考虑。这给我们未来如何使用地球气候系统模式提供了一个参考,即不一定依赖模式直接的模拟结果,还可以利用模式建立起广泛的约束关系,通过与过程理解、不同时期观测数据的结合得到一个更为综合和自洽的结果。

通过本文解读,可以发现,不同证据线有各自优缺点,过程理解从能量框架出发,物理意义更为明确,但无法直接考虑模态效应;仪器记录的数据更加可靠,但气候未达到平衡态,气溶胶这类短寿命的强迫因子会形成干扰;古气候数据的优势是气候达到了平衡态,但数据的可靠程度较差,且冰盖长期反馈需要特殊处理;萌现约束技术本身还不够成熟。各个证据线之间并非严格独立,但它们都从各自关注的角度出发,获得了彼此较为一致的结果,这至少使得AR6对ECS和TCR的评估结果是从各个角度出发自洽的。在未来的气候敏感度研究方面,仍应该发挥各个证据线的优势,其中,过程理解、仪器记录和古气候数据都是对ECS和TCR的直接计算,当这些方法无法有效减小它们的不确定性时,萌现约束可能提供了一个途径。