基于毫米波雷达的室内目标检测与跟踪算法

常浩, 殳国华, 胡博文

(上海交通大学 电子信息与电气工程学院,上海 200240)

0 引 言

随着工业物联网的发展,人们对于室内监控的需求不断增加。近年来,有学者通过摄像头监控、WiFi定位和红外线等技术实现了室内人员的定位与跟踪。采用摄像头监控可以清晰识别室内人员位置,但是遇到障碍物无法工作,且过分采集人员隐私;基于WiFi的定位技术克服了这些缺点,但是很难实现较高的检测精度;红外线传感器尺寸小,成本低,但是易受光照等环境影响。而毫米波雷达克服了这些技术的缺点,且具有更高的检测精度[1］,采用毫米波雷达进行室内目标检测与跟踪有独特的优势。

在基于毫米波雷达的目标检测中,通过对雷达信号的混频与调制,对目标的距离、速度和角度信息进行测量估计,进而对目标运动轨迹进行跟踪。东南大学毫米波雷达实验室已经完成了8 mm波段的倍频器、混频器等芯片的研究。李方敏等[2］提出应用于室内的基于双频连续波比相测距的局部速度差补偿算法,获取高精度的定位信息。

本文提出了一种基于毫米波雷达调频连续波(frequency modulated continuous wave, FMCW)的目标检测与跟踪算法。通过对雷达信号的预处理和快速傅里叶变换(fast Fourier transform,FFT)提取出目标的距离、速度和角度信息,经过二维恒虚警检测确定目标位置,然后基于扩展卡尔曼滤波算法跟踪目标的运动轨迹。

1 毫米波雷达原理

本文采用的毫米波雷达设备为德州仪器公司发布的AWR1443BOOST开发板,发射的波形为线性调频连续波,其频率随着时间线性增加,可以将发射信号表示为:

sT(t)=ATcos[2π(f0t+St2/2)+φ0]

(1)

式中:AT为发射信号的幅值;f0为载波的中心频率;S为调频斜率,S=B/T;B为发射信号扫频带宽;T为信号频率抬高周期;t为时间;φ0为初始相位。

假设雷达到目标的距离为R,电磁波在空气中传播速度为c,接收天线接收到的目标信号为:

sR(t)=ARcos{2π[f0(t-τ)+S(t-τ)2/2]+φ0}

(2)

式中:AR为接收信号幅值;τ为接收信号相对于发射信号的固定延时,τ=2R/c。将发射信号与接收信号进行混频可以得到中频信号,如图1所示。

(3)

图1 调频连续波产生 中频信号原理图

中频信号的频率为:

(4)

FMCW雷达信号的频率随着脉冲时间的增加不断提高。根据回波信号的频率信息,估计目标的距离信息:

(5)

由于雷达的中频带宽受ADC采样频率的限制,因此可以推出最大探测距离为:

(6)

式中:Fs为最高采样频率。目标处于相同距离发射多个信号时回波信号的相位不同,利用相位差来计算目标的速度。

(7)

式中:ω为回波信号角频率;λ为回波信号波长;Tc为相邻两个回波信号间隔时间;v为目标速度。由于|ω|<π,最大检测速度为:

(8)

使用两根雷达天线接收回波信号时,目标与两根天线之间的距离差会导致FFT峰值的相位变化,因此可以进行目标的角度估计。

(9)

式中:θ为接收天线与目标的夹角;d为两根接收天线之间的距离。

2 目标检测流程

图2为毫米波雷达目标检测流程。通过混频得频率稳定的中频信号,对中频信号进行ADC采样得到雷达的时域信号。接着对于每个周期的线性调频连续波进行一维加窗与一维距离FFT处理来获取目标的距离信息;对于一帧内的所有线性调频连续波进行多普勒维FFT,以获取目标速度信息;再利用多根接收天线相位差估计目标角度信息。

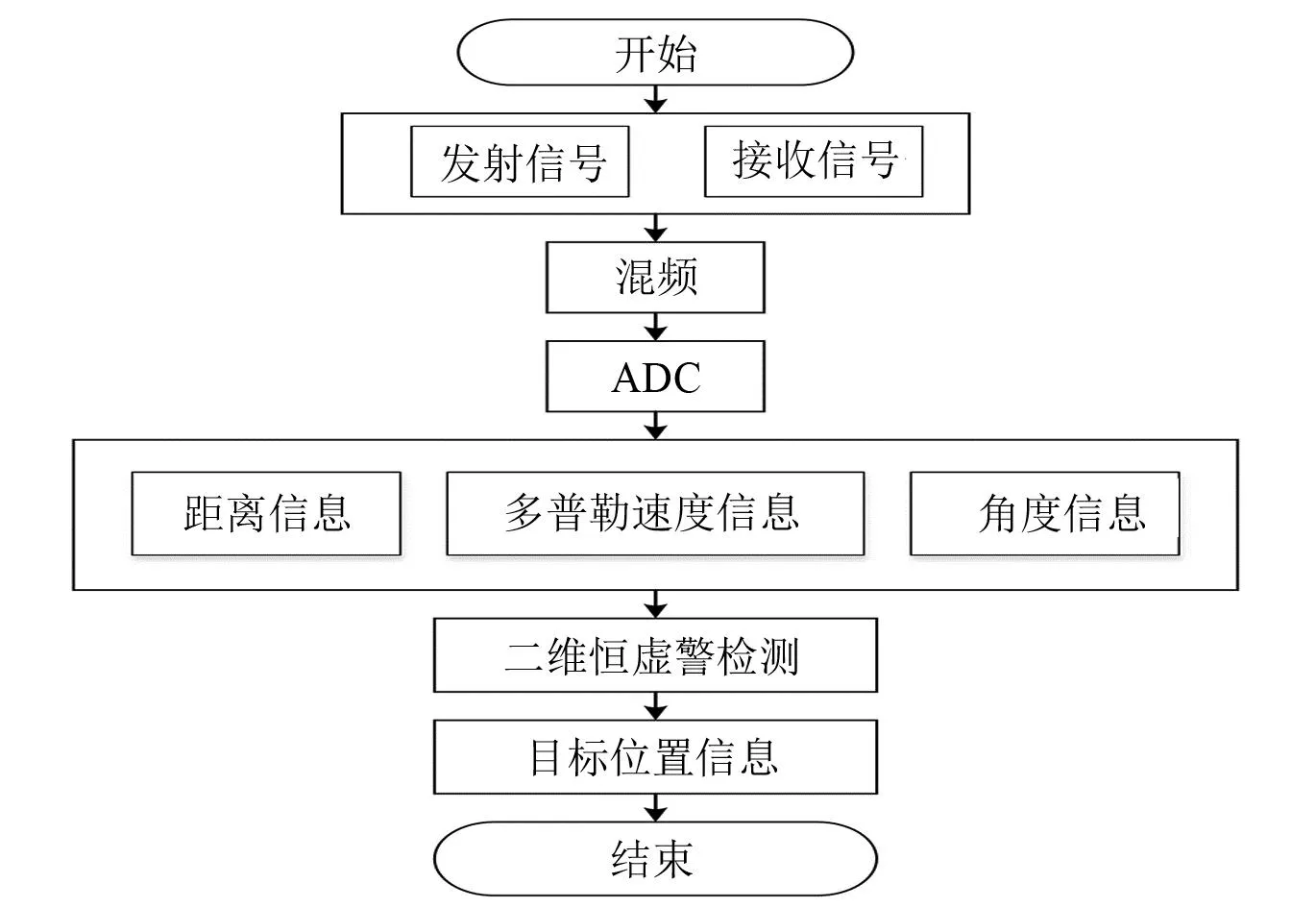
图2 毫米波雷达目标检测流程

雷达接收的信号中含有杂波与噪声干扰,采用二维恒虚警检测可以滤除这些干扰[3］,设噪声分布服从瑞利分布[4］,此时恒虚警检测的检测门限为:

(10)

式中:K为常数;xi为检测单元;n为样本数量;σΛ为单元标准差σ的估计值。自适应的检测门限会随着噪声与杂波信号的大小而改变,有效滤除杂波和噪声干扰,获取目标位置。

3 目标跟踪算法

3.1 基于卡尔曼滤波的跟踪算法

基于卡尔曼滤波的跟踪算法是在线性系统中根据物体在当前时刻的观测位置和前一时刻的最优预测位置[5］,来确定物体在当前时刻的真实位置。线性系统的状态方程和观测方程为:

X(k)=AX(k-1)+BU(k)+W(k)

(11)

Z(k)=HX(k)+V(k)

(12)

式中:X(k)、X(k-1)分别为k时刻和k-1时刻的目标状态;A为状态转移矩阵;B为系统参数矩阵;U(k)为k时刻对系统的控制量;W(k)为系统噪声;Z(k)为k时刻的测量值;H为观测矩阵;V(k)为测量噪声。

使用卡尔曼滤波进行目标跟踪主要基于2个时间更新方程和3个状态更新方程。

时间更新方程为:

X(k|k-1)=AX(k-1|k-1)+BU(k)

(13)

P(k|k-1)=AP(k-1|k-1)AT+Q

(14)

式中:X(k|k-1)为利用上一次状态预测的结果;X(k-1|k-1)为上一次状态的最优预测结果;P(k|k-1)为X(k|k-1)的协方差;P(k-1|k-1)为X(k-1|k-1)的协方差;AT为A的转置;Q为系统噪声的协方差。时间更新方程对系统当前位置进行估计,并计算当前时刻系统预测位置产生的协方差。

状态更新方程为:

(15)

X(k|k)=X(k|k-1)+K(k)[Z(k)-HX(k|k-1)]

(16)

P(k|k)=[I-K(k)H]P(k|k-1)

(17)

式中:K(k)为卡尔曼增益;HT为H的转置;R为测量噪声V(k)的协方差;X(k|k)为当前状态的最优估计值;P(k|k)为X(k|k)的协方差;I为单位矩阵。状态更新方程计算了卡尔曼增益,并根据物体当前时刻的估计位置和当前时刻的观测位置计算物体当前时刻的最优位置及协方差。

3.2 基于扩展卡尔曼滤波的跟踪算法

由于室内目标的运动是非线性的,需要将卡尔曼滤波算法进行扩展,即将物体运动的非线性函数进行泰勒级数展开,将展开式中二阶及以上项略去得到近似线性的模型。

扩展卡尔曼滤波算法的5个基本公式与卡尔曼滤波算法的公式相比,区别在于将系统的状态转移矩阵A和观测矩阵H分别用其Jacobian矩阵代替。

状态转移矩阵代替为:

(18)

式中:f为非线性系统状态转移函数;X为系统状态。观测矩阵代替为:

(19)

式中:h为非线性系统观测函数。图3为基于扩展卡尔曼滤波的目标跟踪算法流程,其主要包含两个阶段:① 预测阶段,通过目标上一时刻的位置信息和速度信息来预测目标当前时刻的位置;② 更新阶段,通过物体当前时刻的观测信息对第一阶段的预测结果进行修正,得到目标当前时刻位置的最优值。

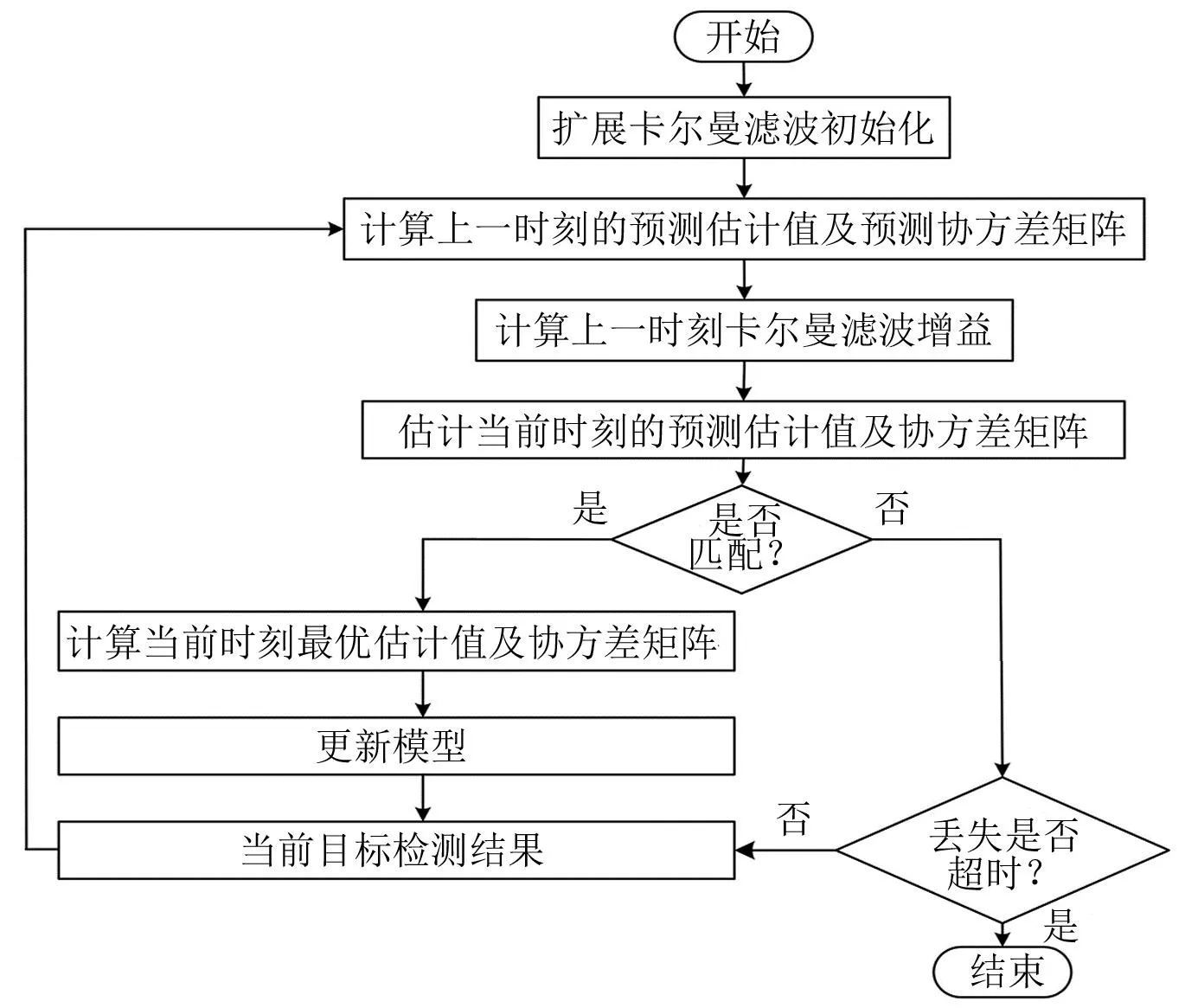
图3 扩展卡尔曼滤波跟踪算法流程

4 试验结果与分析

4.1 试验场景与雷达参数设置

本文试验场所为一间长7.5 m、宽5.0 m、高3.5 m的实验室,雷达架设高度为1.2 m,距离左、右两边墙各2.5 m,距离前端墙7 m。试验设计了三种人员活动方式:① 目标人员依次站在雷达正前方1.0 m、1.5 m、2.0 m、2.5 m、3.0 m、4.0 m、5.0 m、6.0 m处固定位置,原地做踏步动作;② 目标人员从雷达右前方5.0 m处径直走到雷达左前方1.0 m处,行走路线为1字型;③ 目标人员从左前方5.0 m处先走到雷达正前方,然后转身从雷达正前方靠近雷达,行走路线为7字型。试验中雷达系统参数如表1所示。

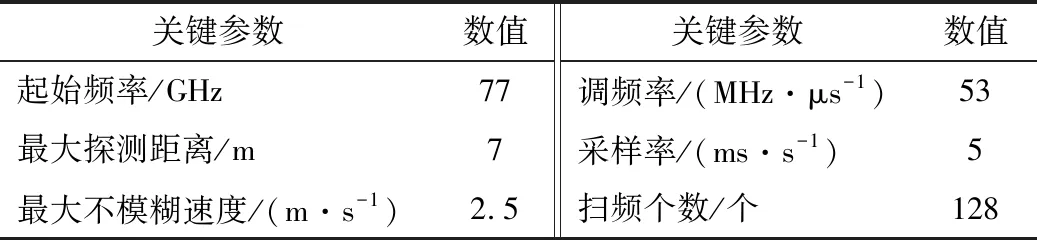
表1 雷达系统参数

4.2 试验结果验证

图4和图5分别为目标人员分别位于距离雷达系统1.5 m和3.0 m时的目标检测二维散点图,可以发现距离雷达较远时散点比较集中,较近时散点比较离散,可以定位人员位置。

图4 距离1.5 m目标 检测散点图

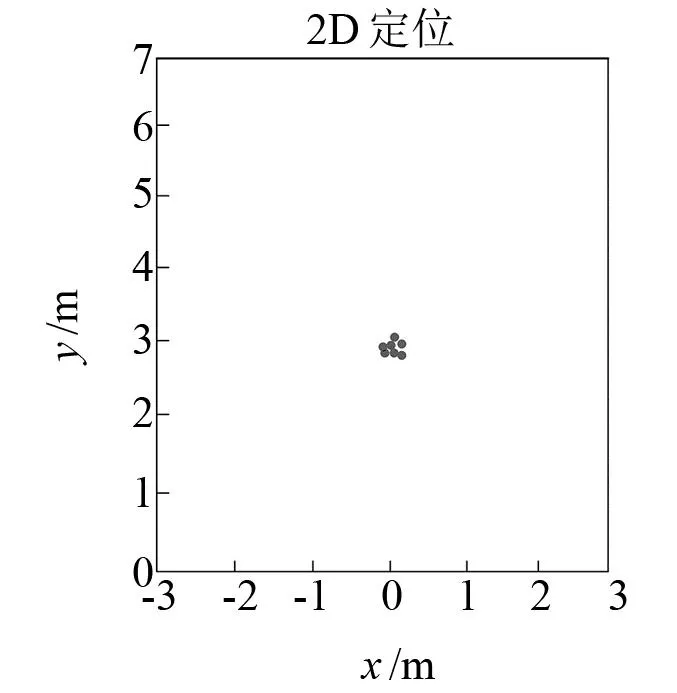
图5 距离3.0 m目标 检测散点图

为了验证目标位置检测的准确性,对选取的8个不同距离的目标位置分别进行检测。表2为检测结果,可以发现:当目标距离雷达超过2 m时定位较为精准;当目标距离雷达较近时,定位误差增大,误差在0.1 m以内。

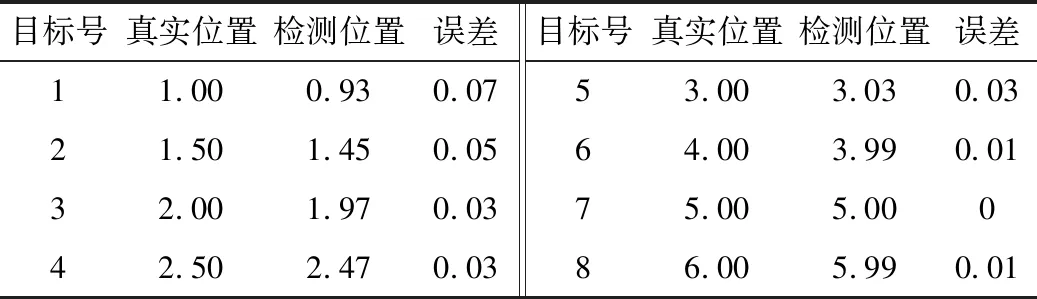
表2 雷达目标检测结果 单位:m

图6和图7表示目标人员运动轨迹为1字型和7字型时,基于扩展卡尔曼滤波的目标跟踪轨迹。可以发现:当距离较远时,检测到的运动轨迹较为平滑;当距离较近时,运动轨迹较为粗糙,可以实现对目标运动轨迹的跟踪。

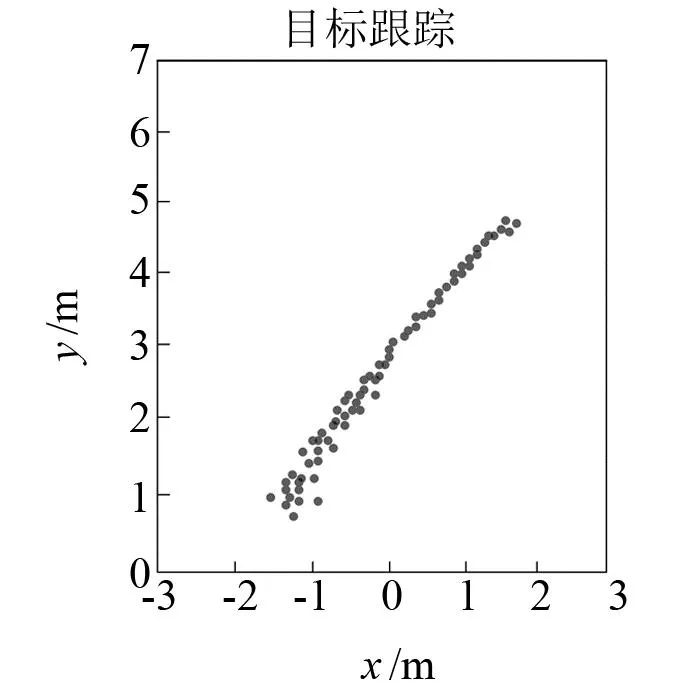
图6 目标1字型运动 跟踪轨迹图

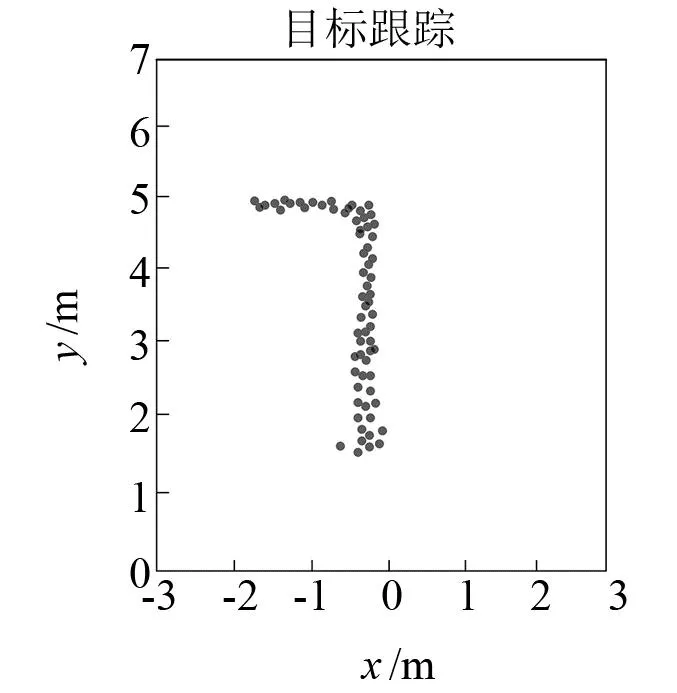
图7 目标7字型运动 跟踪轨迹图

5 结束语

本文提出了一种基于毫米波雷达与扩展卡尔曼滤波算法的室内目标检测与跟踪算法,克服了传统室内监控受环境影响较大等缺点。通过对FMCW毫米波雷达原理的分析和系统参数设计,利用AWR1443BOOST毫米波雷达开发板提取目标距离、速度和角度信息,并设计基于扩展卡尔曼滤波的轨迹跟踪模型,实现精度为0.1 m的室内目标的位置检测和轨迹跟踪。系统具有稳定性好、体积小和功耗低的优点,在智能监控及健康检测等领域具有广阔的应用前景。