基于接入风电功率突变的直流 输电换相失败辨识方法研究
曹伟杰, 万达, 魏武, 季振亚, 王维
(1. 国网江苏省电力有限公司无锡供电公司,江苏 无锡 214000;2. 南京师范大学 电气与自动化工程学院,江苏 南京 210046)
0 引 言
在国家碳达峰、碳中和战略背景下,大规模风电等新能源接入电网,电网的整体架构也随着经济、社会的发展,逐渐成长为以新能源为主体的新型电力系统[1]。当风电等新能源并入受端电网时,由于风电等新能源普遍具有间歇性和波动性,高比例新能源接入会造成交流母线电压波动,可能导致直流输电发生换相失败,对电网的安全稳定运行带来了巨大的挑战[2]。
虽然换相失败的预测判据已有大量的理论研究,但直流输电系统下不同层面的影响因素众多复杂。因此为准确掌握换相失败特性,文献[3]综述了直流输电系统中的换相失败问题,分析了换相失败的发生机理和影响因素。文献[4]提出了采用临界换相电压降来评估交流系统中高压直流输电系统的运行特性。
针对新能源接入电网对电网电压的影响,文献[5]根据双馈风电机组的励磁特性和暂态响应特性,分析了双馈风电机组对系统暂态功角稳定性和电压稳定性的影响。文献[6]利用随机微分理论对系统进行建模分析,探讨了风电功率波动对系统暂态稳定性的影响。
本文提供一种基于潮流追踪与功率变化影响换相失败的辨识方法,针对不同的接入节点,功率变化的影响不同,需要对不同的拓扑分别进行计算。本文在提出通用计算方法的基础上,以某地区直流输电电网为例,进行算例验证。
1 直流输电临界换相电压降
1.1 风电并网下的直流输电系统
风电并网下的直流输电系统如图1所示。
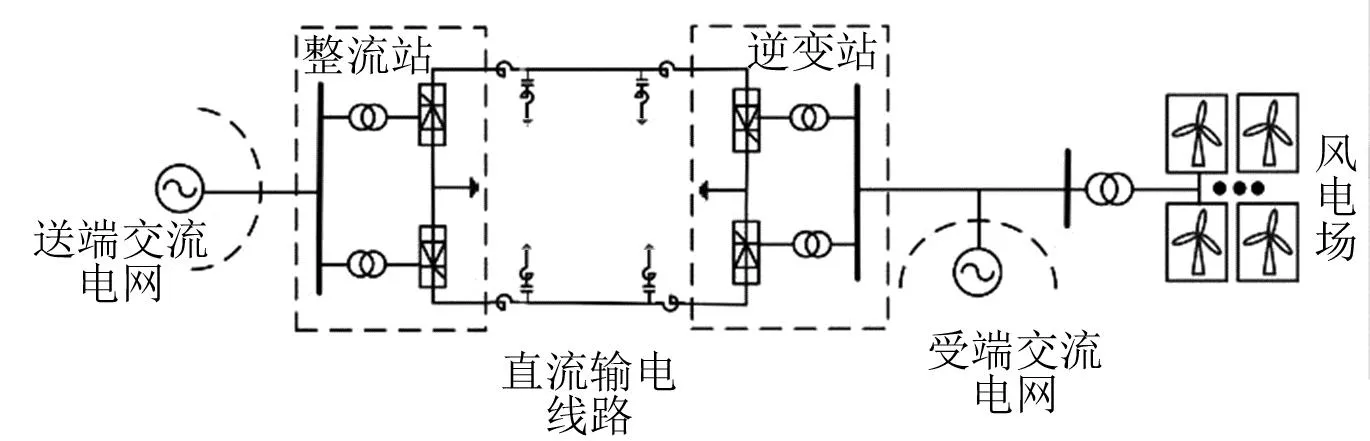
图1 风电并网下的直流输电系统
系统包含交流电网、整流换流站、逆变换流站和风电场。本文对风电接入受端电网后的影响进行了分析。
1.2 临界换相电压降
换相失败是直流输电中换流站最为常见的故障。本文主要分析交直流混联系统下逆变站换相失败的机理,可用超前熄弧角ϒ公式说明:
(1)
式中:Um为逆变侧交流母线电压最大值;Id为直流侧电流;k为换流变压器变比;Xc为换相电抗;β为逆变侧超前触发角。本文认为当γ<7°时换流站发生换相失败。

(2)
由式(2)可推出临界换相电压降落ΔU1:
(3)
2 分析和讨论
2.1 风电并网对换相失败的影响分析
风电并网的系统简化图如图2所示。
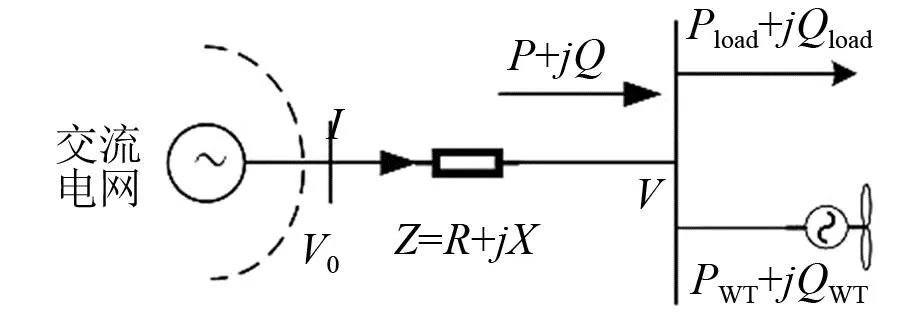
图2 风电并网系统简化图
图2中:V0为主网系统电源侧电压幅值;Z为等值阻抗;P、Q分别为电网系统电源向负荷方向输送的有功和无功功率;V为并网点节点的电压幅值;Pload、Qload分别为并入点节点负荷的有功和无功功率;PWT、QWT分别为接入点风电发出的有功和无功功率。
图3为风电并入点上的戴维南等效电路图。
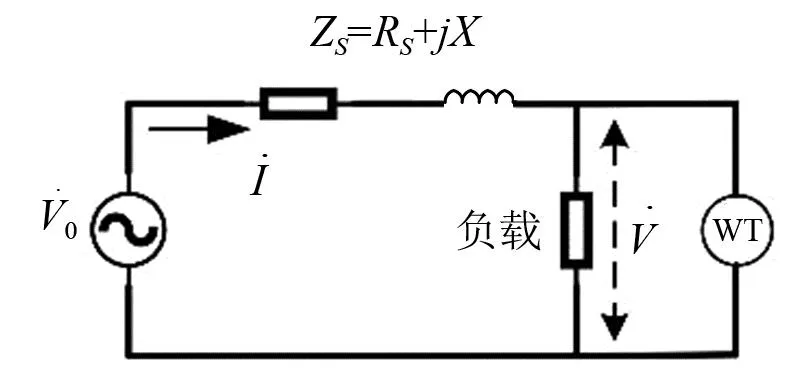
图3 风电接入点的 戴维南等效电路图
风电注入功率改变时,会使线路上的电流产生ΔI的变化。由图3的等效电路计算出风电并入电网或者当发电量波动时,在并入点上的电压变化值。
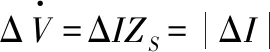
(4)
根据式(4)可以推出并入点的电压为:
(5)
式中:φ为风电并入点的电网阻抗角;ZS为电网等效阻抗;ΔSWT为风力发电注入功率的变化量;V为风电接入点电压;SK为风电并入点处的短路容量;θ为风力发电的功率因数角;V′为风电注入功率改变后并入点的电压。
2.2 风电并网对逆变侧换流母线电压影响分析
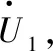
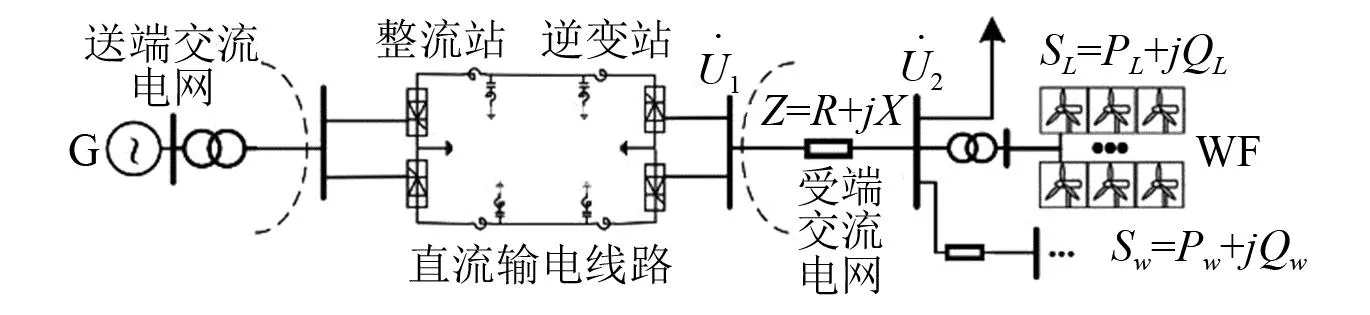
图4 风电接入交直流混联电网结构示意图
(6)
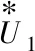
将式(6)中的实部与虚部分开可求得:
(7)
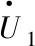
由式(7)可求得有功功率和无功功率,并将式中的P、Q分别对U1r、U1i、R、X和U2求全微分得到微分方程,将得到的微分方程用差分方程替换,结合式(7)可得到如下方程组。
(8)
式中:t为风电接入功率发生改变前;t+1为当风电接入功率发生改变后的时刻。
因此可以推出t+1时刻换流母线电压的变化值为:
(9)
(10)
2.3 风电接入功率最大变化量修正值
根据文献[8]提出的潮流追踪方法,基于顺流功率追踪和逆流功率追踪得到相对应的支路潮流计算。
2.3.1 顺流功率追踪
定义顺流功率矩阵SA为:
(11)
式中:Sij为节点i向节点j流入的功率;Si为节点i的功率。
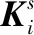
(12)
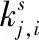
根据上述分析易得分配系数为:
(13)
2.3.2 逆流功率追踪
与顺流功率追踪的方式相同。根据矩阵的定义易得定义逆流功率矩阵SB为:
SA=(SB)T
(14)
因此分配系数为:
(15)
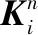
2.3.3 支路潮流追踪
根据上面分析可得:
(16)
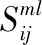
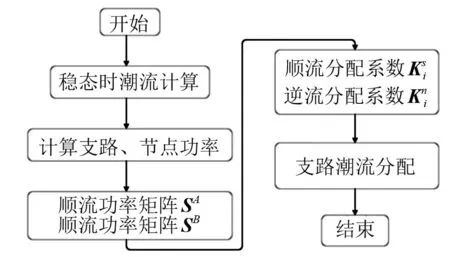
图5 潮流追踪流程图
2.3.4 风电接入功率最大变化量修正值
(17)
式中:Bml为风电机注入换流站节点功率所占风电接入电网总功率比例。
根据式(10)和式(17)可得修正后风电接入功率最大变化量为:
(18)
3 风电并网引发换相失败辨识方法
本文研究了风电接入功率变化量与风电接入功率最大变化量之间的关系,提出风电并网引发直流换相失败关联因子。其表达式如下:
(19)
(20)
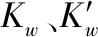
综上所述,风电引发直流换相失败辨识方法流程如图6所示。
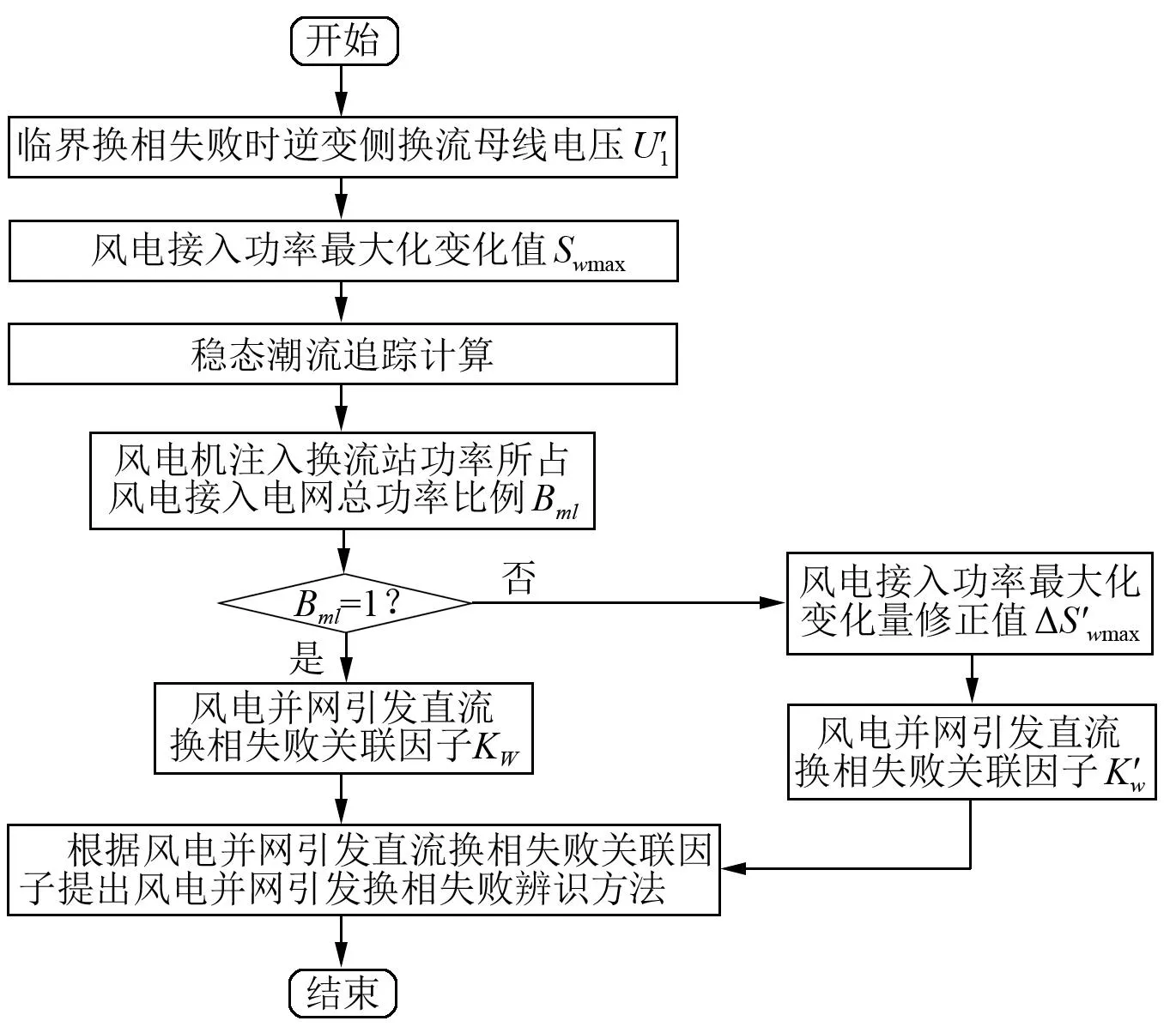
图6 风电引发直流换相失败辨识方法流程图
以修正前风电并网引发直流换相失败关联因子为例,提出风电并网引发直流换相失败的辨识方法:当Kw>1时,逆变站发生直流换相失败;当Kw<1时,系统各节点发生电压波动但保持运行;当Kw=1时,处于临界换相失败。
4 算例分析
4.1 电网网架及参数
本文以某一地区直流输电电网为基础的算例进行说明。直流输电网架结构如图7所示。
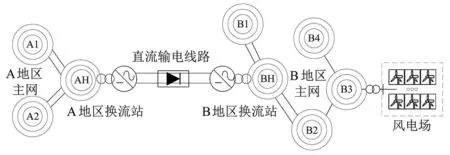
图7 直流输电网架结构
图7为±800 kV特高压直流工程。A地区为送端交流电网,整流侧AH为换流站经两台750/500 kV联络变接入A地区750 kV主网相联。AH换流站750 kV母线出线4回,分别至A1两回和A2两回。在受端B地区电网,逆变侧BH换流站通过4回500 kV接入B地区主网,BH分别至B1两回和B2两回,其中换流母线额定运行电压为525 kV。风电场经升压变压器接入B地区主网。
通过潮流计算可得,A1与A2向AH提供有功功率6 500 MW和无功功率1 544.8 Mvar,BH向B1输送有功功率1 440.7 MW和无功功率217.3 Mvar,BH向B2输送有功功率4 706.9 MW和接收无功功率200.2 Mvar。
4.2 仿真分析
风电场经过升压变压器接入B3,风电场的接入最大功率为6 000 MVA。根据潮流追踪可知,风电场经B3注入B2的功率为3 960 MVA,其占风电接入总功率的比例为0.66。
为验证本文提出的风电接入功率最大变化量修正值,进行仿真试验。风电接入功率变化如图8所示,逆变站关断角如图9所示。

图8 风电接入功率变化图
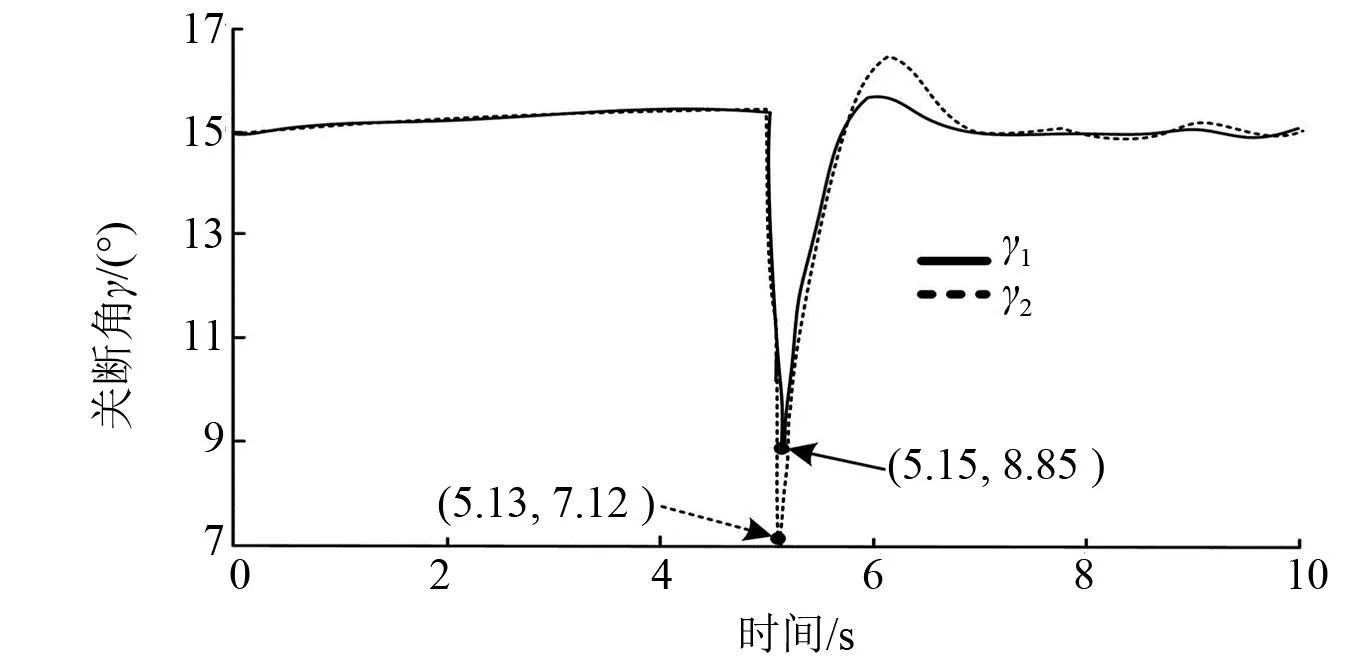
图9 逆变站关断角变化图
图8和图9中:γ1、Sw1分别为风电接入功率变化量为2 124 MVA时候的关断角和风电接入功率;γ2、Sw2分别为风电接入功率变化量为3 218 MVA时候的关断角和风电接入功率。
由图8和图9可知,当未修正前,系统在5 s时风电接入功率瞬时减少了2 124 MVA,此时关断角在5.15 s时从15°跌到8.85°,换流站未发生直流换相失败。根据电网数据显示,此时对于换流站节点真实风电功率变化量为1 402 MVA,并未达到最大变化量,因此换流站未发生直流换相失败。由此可得,当修正前的风电接入功率最大值时,还存在26.4%的误差,因此需要对风电接入功率最大值进行修正。
当采用风电接入功率修正值时,系统在5 s时风电接入功率瞬时减少了3 218 MVA,此时关断角在5.13 s时从15°跌到7.12°,此时处于临界换相失败。根据电网数据显示,此时对于换流站节点真实风电功率变化量为2 124 MVA,达到最大变化量,因此换流站此时发生临界换相失败,验证了本文提出的修正风电接入功率最大变化量方法的准确性和可行性。
由计算所得风电接入功率最大修正值,与临界关断角7°相比,还存在1.7%误差。这是由于当风电接入功率瞬时改变时,换流母线电压瞬时下降,但是系统其他发电机为其支撑,导致电压向上抬升,造成计算得到的风电接入功率最大变化量修正值有一定误差。
为验证本文提出的风电并网引发直流换相失败的辨识方法,通过某地区大网进行仿真验证。风电接入功率变化如图10所示,逆变站关断角如图11所示。
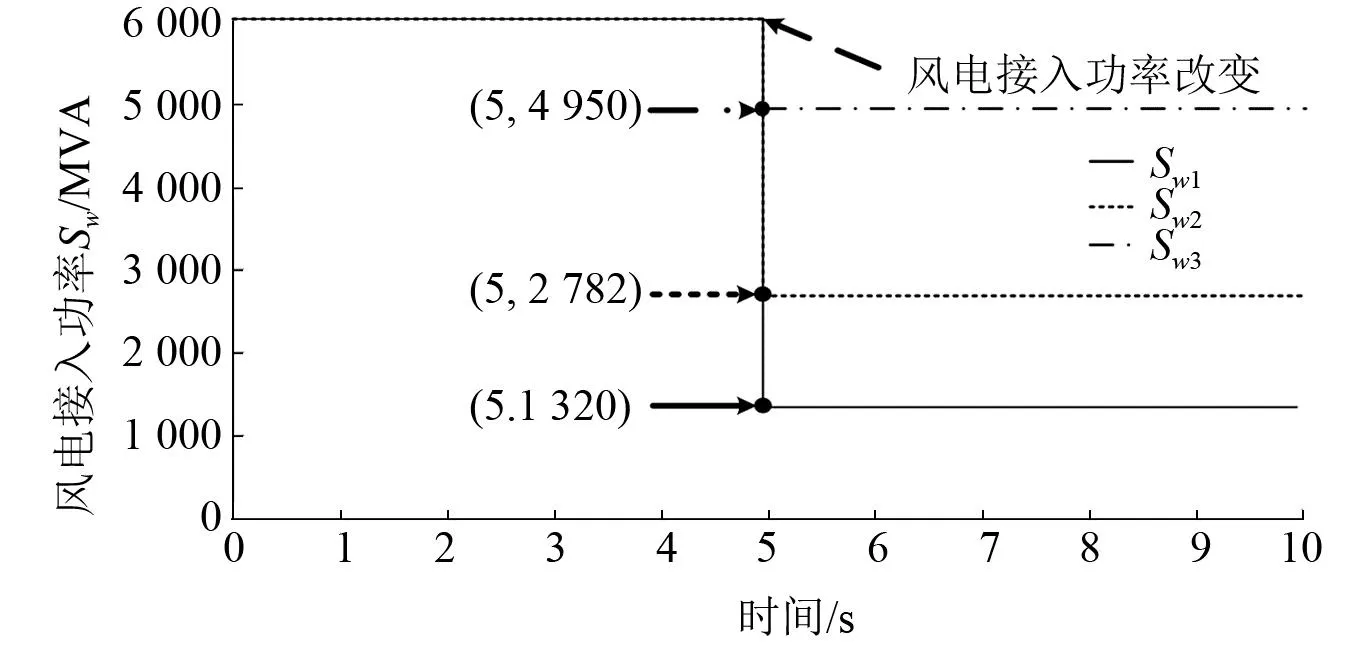
图10 风电接入功率变化图
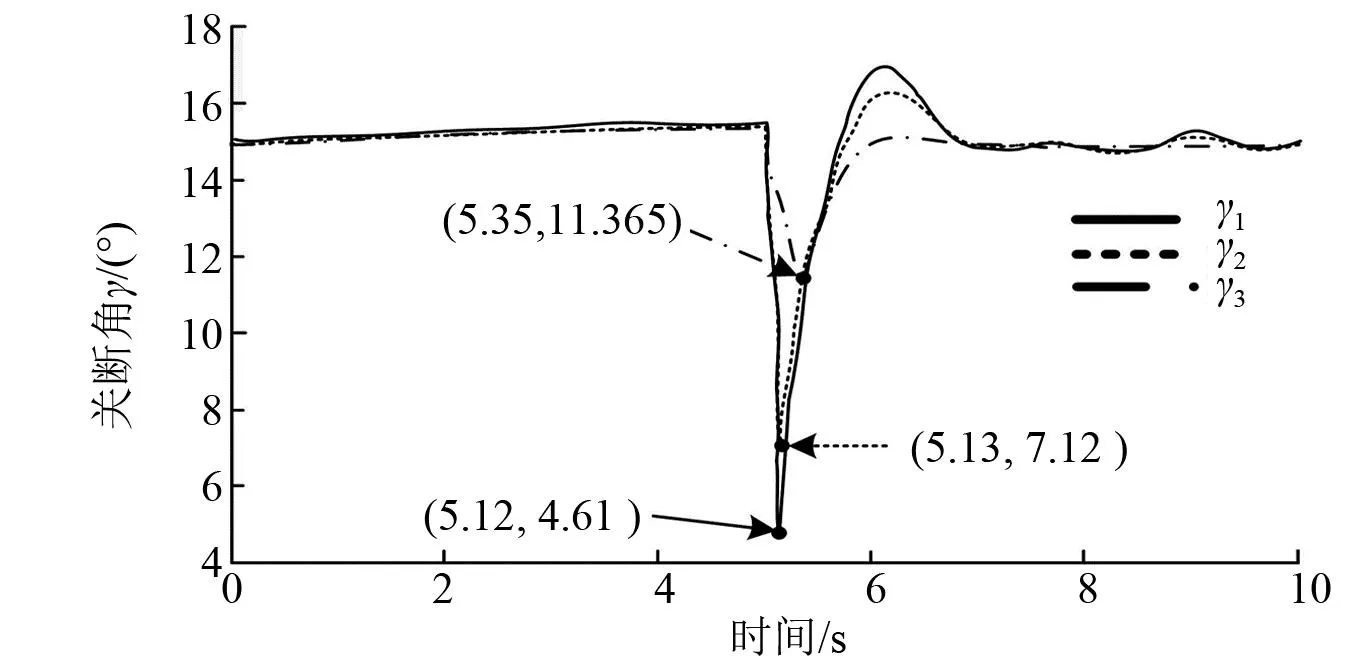
图11 逆变站关断角变化图
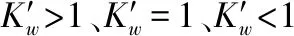
通过上述仿真分析,验证了提出的风电并网引发直流换相失败的辨识方法的准确性和有效性。
5 结束语
本文提供一种基于潮流追踪与接入风电功率突变的直流输电换相失败的辨识方法。针对不同的接入节点,功率变化的影响不同,因此需要对不同的拓扑分别进行计算。首先推出风电接入功率最大变化量ΔSwmax表达式,通过分析在不同电网结构中,风电注入换流站的功率并不等同于风电并网的总功率,因此需要对风电接入功率最大变化量进行修正。在此基础上,定义风电并网引发直流换相失败关联因子。最后根据关联因子提出风电并网引发直流输电换相失败辨识方法,并在提出通用计算方法的基础上,以某地区直流输电电网为例,通过算例验证了其准确性和有效性。

