新能源场站风功率曲线异常数据处理算法

李宣谕

(大唐东北电力试验研究院有限公司，吉林 长春 130102)

0 引言

近年来,随着国家能源政策调整,我国风力发电规模逐年增长,已在整体能源布局中占据着重要地位。风功率曲线作为重要性能指标,是开展风电机组数据分析的基础[1],相关分析研究工作随着新能源发展逐年推进。风电企业在日常运行过程中,受外部环境干扰、风机运行故障、弃风限电等因素影响[2],风电场数据采集与监视控制(supervisory control and data acquisition,SCADA)系统存在大量的异常数据[3]。如果这些数据不加以处理直接应用,较差的数据质量会造成拟合的风机实际功率曲线发生畸变,干扰机组运行特性分析,影响风电机组生产经济性与运行状态评估结果[4]。因此,对风电机组功率数据进行异常数据识别与清洗,提取高质量数据是不可缺少的环节[5-6]。

现阶段常用的风电机组功率数据识别方法可分为以下几类:(1)基于统计分析的异常数据识别方法,主要有3sigma法[7]、四分位法[8]、组内最优方差[9]、变点分组[10]、Thompson tau[11]、云分段最优熵[12]和Copula理论[13]等算法;(2)基于机器学习的异常数据识别方法,主要有k-means算法[14]、基于密度的空间聚类DBSCAN(Density-Based Spatial Clustering of Applications with Noise)算法[15];(3)基于图像的异常数据识别方法,主要有基于图像边缘识别的技术[16]、基于图像分割技术[17]与基于图像像素技术[18]三种方法。不同的异常数据识别方法在实际应用过程中具有各自的特点,其中,四分位法异常数据识别速度较快,对离散型数据识别效果较好,通用性强,稳定性好,但在异常数据占比较大时,辨识效果不佳[19]。DBSCAN算法可有效实现分散型数据的识别,并可用于一维或多维特征空间,但对堆积型数据识别能力较差[20],图像处理技术对异常数据识别较慢,对各类异常数据识别效果相对较好,但技术实现难度较高,无法区分出切出风速附近的虚假异常数据[21]。

针对以上问题,本文提出将DBSCAN算法与四分位法进行优势结合,构建基于DBSCAN-分段四分位的组合算法,通过DBSCAN算法对风功率样本数据聚类分析,将异常数据簇类别与特征进行区分,再利用四分位法把离散的堆积型异常数据剔除,完成风速-功率数据处理。经过代入某风电机组实测数据,比较分析组合算法、标准DBSCAN算法与四分位法对样本数据异常识别与清洗的效果,验证了所提方法的可行性及在数据处理方面的优势。

1 算法介绍

1.1 DBSCAN算法

DBSCAN算法是一种基于空间数据密度的聚类算法[22]。该算法的优势是不需要预先约定分类的数量,完全依靠数据本身质量进行分类,可对任意形状分布的稠密数据进行聚类,聚类结果没有偏倚。缺点是聚类结果受两个参数初值影响较大[23],在样本数据密度分布不均匀或聚类间距差距较大时,聚类质量较差[24]。计算流程如下:

(1)预先确定参数邻域半径Eps与最小数据点集合个数Minpts;

(2)以样本数据中任意一个从未访问点开始,以Eps为半径距离,如果在这个邻域半径范围内分布的其它数据点个数大于或等于集合个数Minpts,则标记为正常数据,如小于Minpts,则标记为异常数据;

(3)返回上一步,代入新的数据点进行计算,直到所有数据计算完毕;

(4)剔除异常数据集,将正常功率数据保留。

1.2 四分位算法

四分位法是一种通过度量数据分布位置进行异常数据识别的方法。在对离群数据点分析处理时,不需要事先假设数据服从某种分布,可有效分析数据集群体分布特征,去除数据中离群值的影响,数据处理效果较为稳定[10]。计算方法如下:

(1)风功率样本数据集中,功率的个数记为n,并按功率从小到大排列。

(2)当(n+1)/4可以整除时,如式(1)所示。

(1)

式中:Q1为第0.25(n+1)位的功率数值;Q2为第0.5(n+1)位的功率数值;Q3为第0.75(n+1)位的功率数值。

(3)当(n+1)/4不能整除,且n=4k+4,(k=1,2,3,…)时,如式(2)所示。

(2)

式中:Q1为第0.25n位功率数值的0.75倍与第(0.25n+1)位功率数值的0.25倍之和;Q2为第0.5n位功率数值与第(0.5n+1)位功率数值平均值;Q3为第0.75n位功率数值的0.25倍与第(0.75n+1)位功率数值的0.75倍之和。

(4)当(n+1)/4不能整除,且n=4k+6,(k=1,2,3,…)时,如式(3)所示。

(3)

式中:Q1为第(0.25n-0.5)位功率数值的0.25倍与第(0.25n+0.5)位功率数值的0.75倍之和;Q2为第0.5n位功率数值与第(0.5n+1)位功率数值平均值;Q3为第(0.75n+0.5)位功率数值的0.75倍与第(0.75n+1.5)位功率数值的0.25倍之和。

(5)剔除异常值。

下边缘限值Llow如式(4)所示。

Llow=Q1-1.5(Q3-Q1)

(4)

上边缘限值Lhigh如式(5)所示。

Lhigh=Q3+1.5(Q3-Q1)

(5)

对每个风速段区间数据进行计算,将数据位置处于Llow～Lhigh范围之外的数据视为异常数据,将其剔除,保留下的数据则为风功率正常数据。

1.3 DBSCAN-分段四分位法

首先采用DBSCAN算法,根据样本数据特征划分数据簇类别,剔除部分异常数据簇。然后,将样本数据以风速分布为基准等间隔划分,分段使用四分位法,进一步识别少部分堆积型异常数据与离群数据特征不明显的异常点。计算流程如图1所示。

图1 DBSCAN-分段四分位算法流程图

2 风电数据实例分析

2.1 算法应用流程介绍

以国内云南某风电场20号风机实测运行数据为例,如表1所示。选取2021年9月1日至2022年9月1日的实测数据,采样间隔10 min,共计47 837组数据作为样本数据。分别采用DBSCAN法、四分位法和DBSCAN-分段四分位法进行异常数据处理,对比分析异常数据清洗效果,验证算法性能。

表1 某风场20号风机风速-功率数据

采用DBSCAN法对样本数据进行异常数据识别,其中核函数邻域半径Eps与最小数据点集合个数Minpts可通过k-distance方法确定,如表2所示。

表2 k-distance对核函数寻优结果

将参数寻优结果代入标准DBSCAN法,经测试,核函数Minpts=19,Eps=0.006对异常数据识别效果最好,标准DBSCAN法对异常数据识别结果如图2所示。其中,蓝色数据点为正常数据,红色数据点为异常数据。由图中可以看出,在机组进入切入风速以后,少部分零功率异常数据点未能辨别。其原因是由于算法自身的局限性,满足算法规则的少量的堆积型异常数据未能有效识别。

图2 DBSCAN法对异常数据识别结果

运用四分位法进行数据处理时,不建议直接进行异常数据清洗。当部分区间数据占比较小时,少部分正常数据可能被认为异常数据删除,导致清洗后的数据不完整,拟合功率曲线后初始值不是从0开始,如图3所示。

图3 四分位法对异常数据识别结果

本文建议以风速为基准,将样本数据等间隔划分40组数据段或60组数据段,每段数据区间的风速-功率数据采用四分位法进行异常数据识别,剔除异常数据后再将各区间的正常数据重新组合,采用分段四分位法效果如图4、图5所示。

图4 四分位法(划分40组数据)对异常数据识别结果

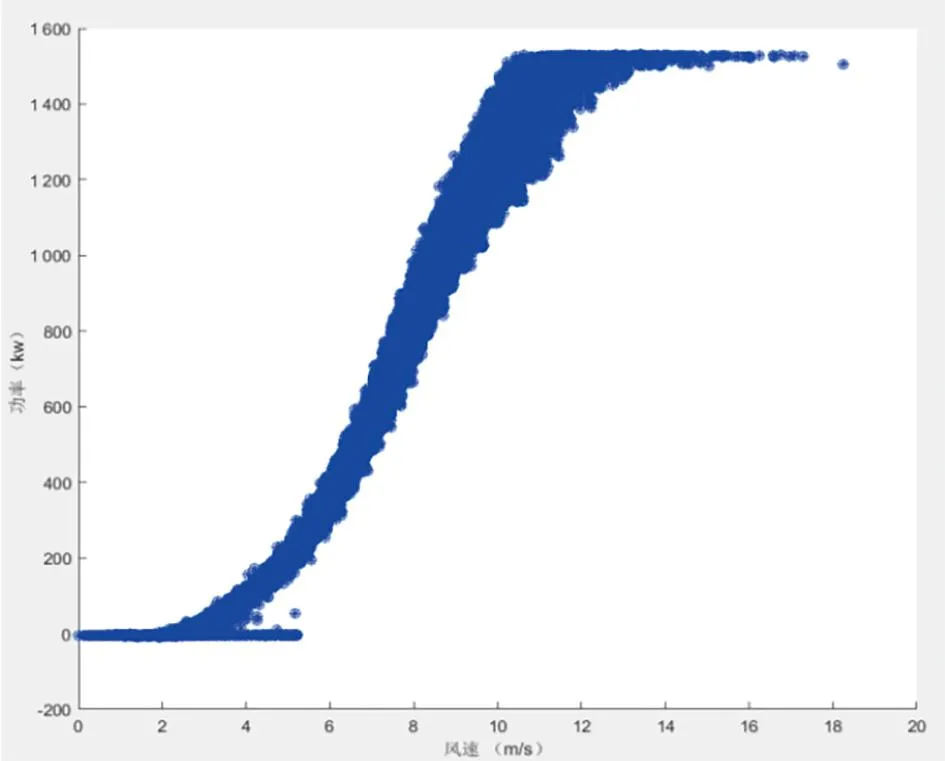
图5 四分位法(划分60组数据)对异常数据识别结果

为了提高算法对样本数据特征识别准确性,将数据按区间划分,分段进行四分位法计算,克服局部堆积型数据对整体异常数据识别效果的影响。由图4、图5可以看出,并不是数据段划分越多对异常数据识别效果越好,受限于算法规则,数据区间划分越多对局部堆积型异常数据越敏感,分段四分位法也无法完全识别局部占比较高的异常数据。因此,划分数据段区间个数应选择较为适合的值。

根据本文所提方法,先通过DBSCAN法剔除大部分异常数据,再通过分段四分位法(划分40组数据)将少部分堆积型异常数据剔除,结果如图6所示。

图6 分段四分位法对异常数据处理效果

数据处理结果如图7所示。

图7 DBSCAN-分段四分位算法对异常数据清洗效果

经数据处理后,保留正常数据47 693组,异常数据剔除率为0.3%,被清洗的异常数据集中存在少量被误删的正常数据,对原始数据的完整性和充裕度造成了一定影响,但这部分占比不高,清洗后的正常数据仍可完全表征风功率曲线全行程特性。此外,由图7可以看出,通过DBSCAN-分段四分位算法对样本数据处理,已将离散、横向分布的异常数据完全剔除,提取的风速-功率数据质量较好,数据清洗效果优于标准DBSCAN法和四分位法。

2.2 算法实例应用验证

采用本文所提方法对辽宁某风电场8号风机的运行数据进行异常数据识别分析。该风机的机组型号为H111-2.0 MW,切入风速3.0 m/s,切出风速25.0 m/s,额定风速11.5 m/s。样本数据选取2022年7月1日至2023年6月30日运行数据,采样间隔10 min,共计54 870组数据作为样本数据,验证算法实际应用效果,数据如表3所示。

表3 辽宁某风场8号风机风速-功率数据

绘制8号风机实测数据的散点分布如图8所示。

图8 8号风机实测数据散点分布图

从图8中可以看出样本功率数据存在大量的横向分布的堆积型异常数据以及曲线周围的分散型异常数据,这两类异常数据主要由弃风限电、通信设备故障、机组计划外停机检修等随机因素造成。该机组理论功率曲线参数如表4所示。

表4 辽宁某风场8号风机理论功率曲线参数(空气密度=1.225 kg/m3)

经数据处理,剔除异常数,筛选正常数据51 293组,剔除异常数据3 577组,保留正常数据占比93.481%,异常数据识别占比6.519%,风功率数据清洗效果如图9所示。

图9 8号风机功率曲线示意图

图9中,红色散点数据为数据清洗后的正常数据,蓝色曲线为主机厂家提供的标准功率曲线,绿色曲线为8号风机实际功率曲线。该效果图可较好地用于风机功率曲线分析,如分析风机功率一致性等。经核算,该场8号风机功率一致性系数在合理范围内。

3 结束语

本文通过分析DBSCAN法与四分位法对异常数据的识别效果,提出基于DBSCAN-分段四分位的组合算法对风功率异常数据进行辨识。以某风电场实测风功率数据为基础,验证本文所提方法的有效性,结论如下。

(1)基于DBSCAN-分段四分位的组合算法,可实现对分散型、堆积型异常数据的有效识别,在风功率异常数据识别与清洗方面有较好应用。且算法原理简单,易于实现,处理速度适中,清洗效果稳定、可靠。

(2)基于DBSCAN-分段四分位的组合算法,将DBSCAN的自适应性与四分位法的通用性优势结合,克服单一算法局限性。通过划分数据区间分段处理,增强对数据局部特征识别准确性,进一步提高算法自身的泛用性能与识别精度,在实际应用中具有一定优势。

(3)通过算例1与算例2分析表明,该组合算法在数据处理时,存在将15.0 m/s以上的正常数据误删的情况,对数据完整性有一定影响,但数据剔除率占比不高,处理后的数据仍可表征风机功率曲线特征,不影响风机功率曲线绘制,满足实际项目的需要,该缺点可通过数据插值法解决。