基于人工智能的萤火虫群优化算法在无线传感器中的应用研究

仇 伟

(国网曲阜市供电公司,山东 曲阜 273100)

0 引言

无线传感网络(WSN)即多个传感器节点在数据传输空间中接收数据信息[1]。每个传感器均具备数据处理的功能,且还能同时拥有多个传感器,所有传感器节点的运行便是传感工作。由于无线传感器存在接收信号、节点能量不足等问题,WSN节点的部署问题及网络覆盖范围因此十分关键,需要重点关注。

1 网络覆盖模型

信息的接收与网络覆盖面有较大关联,选取WSN网络节点时,需要根据网络覆盖面建立模型,求解覆盖范围及覆盖率[2],量化网络覆盖率选择概率感知模型和0/1感知模型。

1.1 0/1感知模型

0/1感知模型可以将一些客观因素排除,在二维空间内应用较广,视传感器节点为区域圆,半径为r,圆心为Ci(xi,yi),若区域内无信号源则则为0,若区域内有信号源需≥1。

假设任意目标点O(像素点)的坐标(xj,yj)在传感器网络监测区内,那么O与圆心的距离为欧氏距离,公式如下:

(1)

O点是否被区域覆盖,判断如下:

(2)

1.2 感知概率模型

在对该方法进行建模时,由于外界条件的变化,本文采用了一种基于认知概率的方法。在实际应用中,所建立的知觉概率模型是可行的。假设2D平面上的监控对象(x,y)是该传感器网络中的一个节点的坐标,并且它可以出现在任何一个地方,记(xk,yk)是该地区监控对象点k的坐标,那么,该传感器网络上的监控概率就可以用Ck(si,k)来表达,即:

Ck(si,k)-

(3)

上式中,re表示可靠的测量参数;Rs为节点感知半径;节点zi与目标点k的欧氏距离以d(zi,k)表示。

2 WSN网络覆盖优化算法

2.1 粒子群优化算法(PSO)

PSO算法采用了一种新的微粒群优化模型,该模型中的每一个微粒群都代表一个自适应函数。粒子具有2个特性,一个是速度,一个是位置。在此基础上,将各粒子在不同的位置上进行优化求解,得到各粒子的最佳解,也就是各粒子的最佳值,而粒子的速度ua和位置xa的更新则由空间最优值和个体最优值决定。当一个循环结束后,最佳的解决方案被称为pa,并且该空间的最佳解决方案被称为f。每个粒子可根据下述公式进行更新迭代:

ua=wua+C1rand()(pa-xa)+C2rand()(f-xa)

(4)

(5)

pa=xa

(6)

上式中,w代表惯性因子,数值越高,粒子空间寻优能力越强,而在局部空间内寻优较弱;rand()表示在(0,1)之间随机出现且均匀分布的数值;C1和C2是粒子的学习因子。所有粒子均出现变化,通过更新速度和位置获取空间及个体最优值,到规定程度时停止。

2.2 萤火虫群优化算法(GSO)

物理空间中存在萤火虫,而萤火虫可以通过荧光素吸引附近的萤火虫,算法存在3个假设:

(1)在同一区域内,如果有一只是雌性或雄性的萤火虫,则会受到附近其他的萤火虫的吸引。

(2)每只萤火虫的视觉范围是受限的(作为决策半径)。随着萤火虫的减少,决策半径变大。

(3)荧光素含量高的萤火虫可以将附近的萤火虫聚集在一起。

如果在i个时间点上,M个萤火虫在n个维度上被随机分割,那么,在t个时间点上,可选择适应度函数为f(xt(i)),萤火虫所在区域可表示为xt(i),荧光素含量可以Lt(i)表示,若决策半径为rt(i),那荧光素含量为:

Lt(i+1)=(1-ρ)Lt(i)+βf(xt(i))

(7)

式中,ρ为荧光素散发后含量;β为荧光素含量。

若设时间段为i,则在i时间段内,两只萤火虫(a和b)相互移动的概率表示为:

(8)

式中,萤火虫(t)在i时间段的决策半径表示为Zt(i)。

设时间段为i,则在第i时间段,萤火虫(t)的所在区域为:

(9)

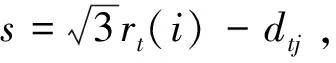
i时刻内,萤火虫t下一刻决策半径为:

rt(i+1)=min{rs,rt(i),α|Nmax-Ni(t)|}

(10)

式中,决策半径的改善率表示为α;决策半径的改善区间表示为Nmax;决策半径值相符合的运动距离表示为rs。

2.3 改进GSO算法(IGSO)

本项目拟结合 PSO与 GSO两种优化方法,建立一种新的基于遗传优化的 IGSO方法,通过对微粒的运动速率、荧光素浓度、判决半径等参数的优化配置,得到微粒的最优判决半径,并对其进行优化求解。在此基础上,通过对粒子运动过程中的位置、速度、荧光素含量等信息进行更新,并结合空间最优解和个体最优解,最终实现粒子的位置和速度更新。

3 仿真实验

3.1 实验内容

综合性对比IGSO、WOA、PSO算法的仿真结果,分析3种算法在无线传感器随机分布问题的改善效率,最后求出覆盖率。性能仿真实验表达了所有算法特点,用控制变量方法改变一个参数,实现参数对覆盖率的影响[3]。以坐标值为研究对象,定义和调整粒子适应值,让其向目标值靠近并达到最优覆盖率。

3.2 粒子规模对实验的影响

3.2.1 粒子规模变化实验参数设置

迭代次数maxgen=400,区域边长L=50,通信半径R=5,离散粒度data=1,最小速度umin=-2,最大速度umin=2,位置最小值popmin=0,位置最大值popmax=50。

3.2.2 粒子规模变化实验

(1)当节点数量为35时,取粒子规模sizepop为80、60、40、20,结果如表1所示。

表1 粒子规模对覆盖率的影响(n=35)

(2)节点数量为45时,取粒子规模sizepop为80、60、40、20,结果如表2所示。

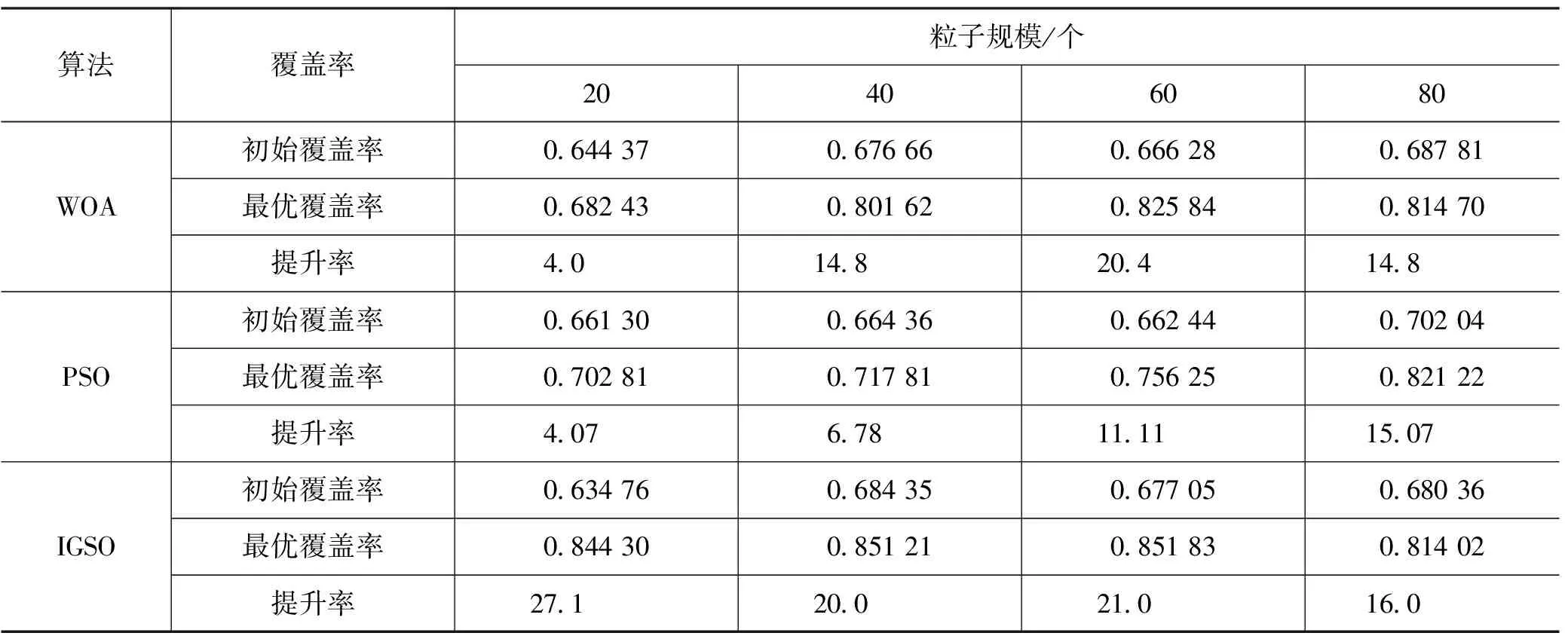
表2 粒子规模对覆盖率的影响(n=45)

由表1—2得出,粒子大小的差异会影响到各类算法的最佳覆盖范围(即增益),增益速率是一个重要的评价标准。节点数相同时,较PSO算法和WOA算法相比,IGSO算法最优覆盖率和提升率均较高。

3.3 迭代次数对实验的影响

3.3.1 迭代次数变化实验参数设置

区域边长L=50,通信半径R=5,离散粒度data=1,最小速度umin=-2,最大速度umin=2,位置最小值popmin=0,位置最大值popmax=50,节点数量n=35,粒子规模sizepop=80。

3.3.2 迭代次数变化实验

迭代次数maxgen=200、300、400、500,覆盖率优化结果如表3所示。

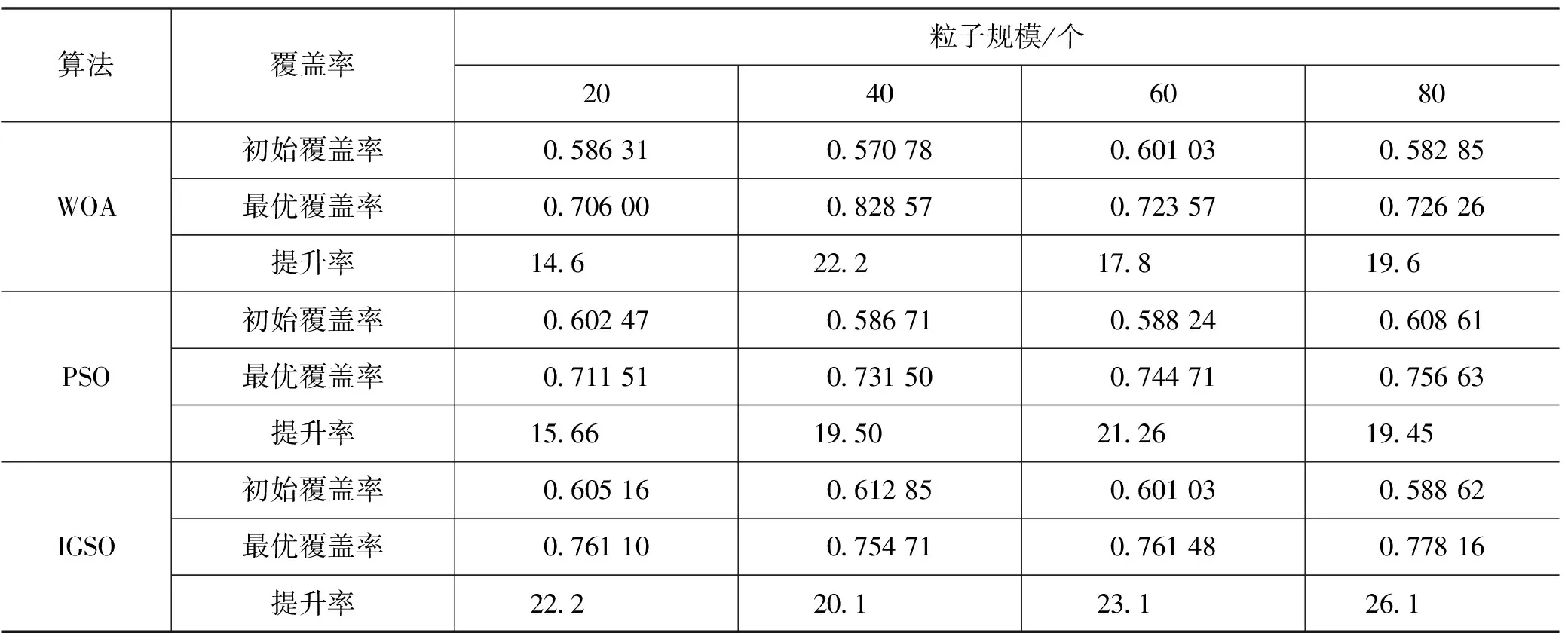
表3 迭代次数对覆盖率的影响(n=35)

由表3可见,迭代次数的增加容易影响覆盖率和提升率,但也有局限性,迭代次数无法决定覆盖率高低。因为3种算法属贪心算法,局部区域出现最优解,且会对空间最优解造成影响,使得迭代数和覆盖范围之间的相关性较弱。在相同的情况下,IGSO算法好于 WOA算法和PSO算法。

3.4 最优实验结果

迭代次数、粒子规模与节点数量中,采用控制变量法变化其中一项,观察实验结果。如图1—3所示,体现了WSN网络中IGSO算法、PSO算法和WOA算法的实验结果。结果显示,IGSO算法网络覆盖率为0.916,与PSO算法和WOA算法相比更优,其中迭代次数=400,通信半径R=5,离散粒度data=1,最小速度umin=-2,最大速度umin=2,位置最小值popmin=0,位置最大值popmax=50,节点数=45,粒子规模=35,符合优秀标准。可见,同等条件下,IGSO算法优于PSO和WOA算法。

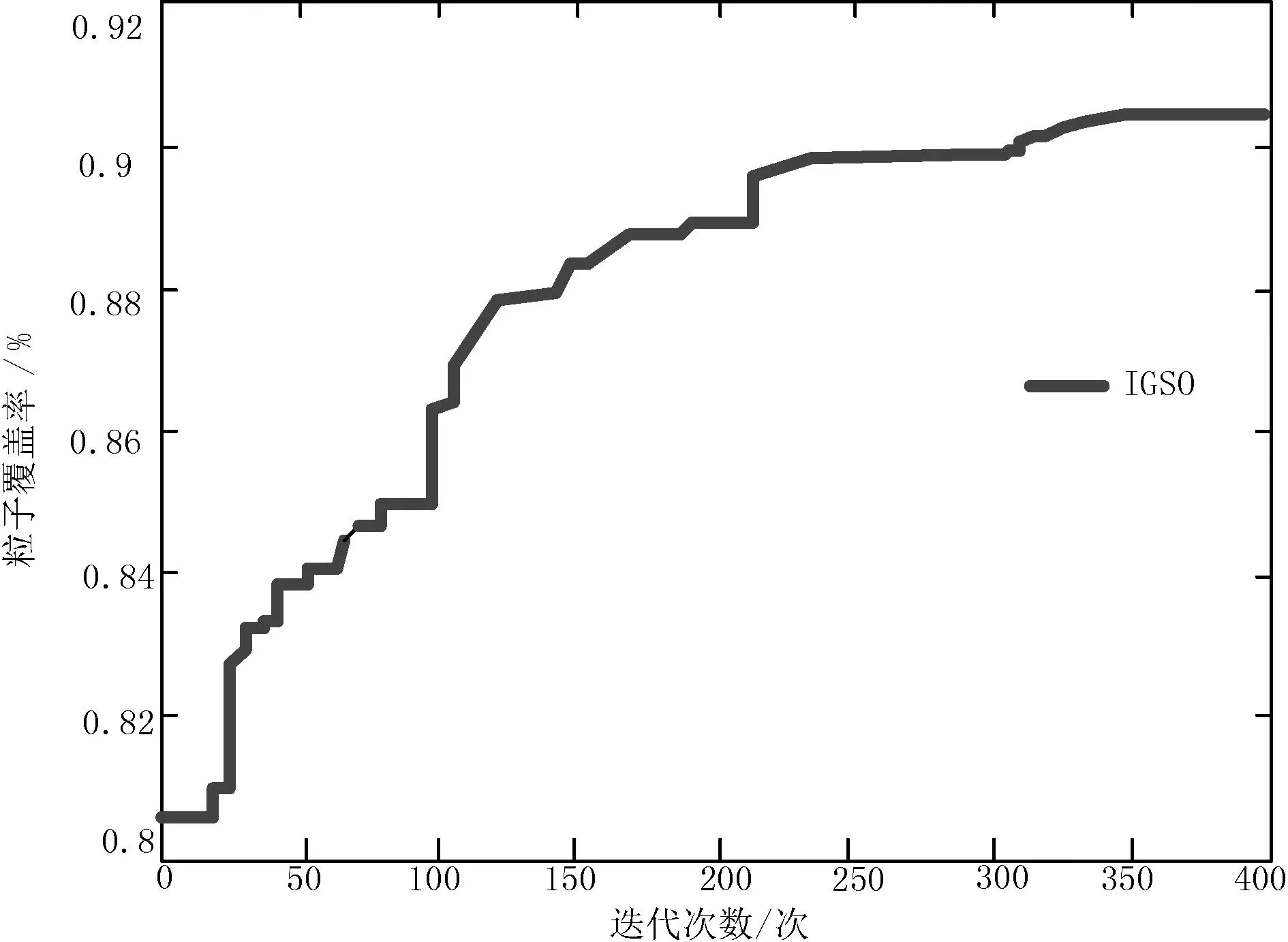
图1 IGSO算法的优化结果和最优覆盖率

图2 PSO算法的优化结果和最优覆盖率

图3 WOA算法的优化结果和最优覆盖率

4 结语

要想整合人工智能技术和无线传感器,需要解决覆盖问题,探究算法,解决无线传感器节点部署问题。本文为使WSN的覆盖范围达到最大目标,给出了WSN的最佳覆盖范围。采用 IGSO方法可以提高系统的覆盖效率,使系统的结点得到迅速的覆盖。仿真效果得出,相同条件下IGSO算法优于PSO算法和WOA算法。