代数中的整体思想及其应用

丁波

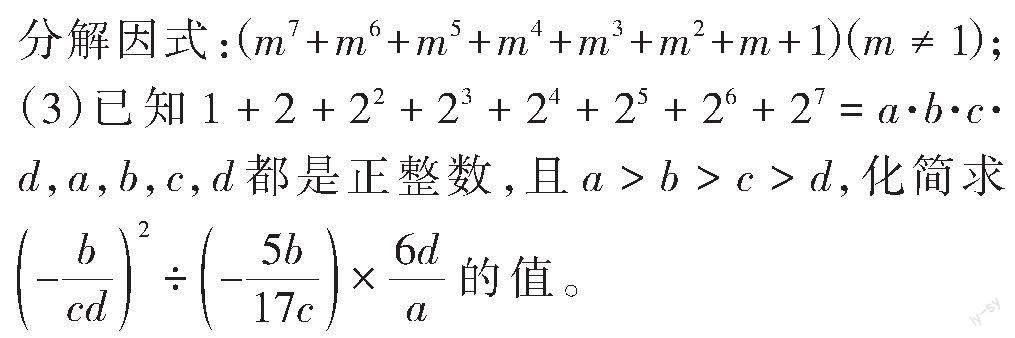
［摘 要］整体思想可以达到化繁为简，变难为易的目的。文章结合五则典例，探讨整体思想在平方差公式、完全平方公式、因式分解、二元一次方程组、分式方程中的应用，以培养学生整体思想意识，提高学生整体解决问题的能力。

［关键词］整体思想；代数；初中数学

［中图分类号］ G633.6 ［文献标识码］  A ［文章编号］ 1674-6058（2023）26-0029-03

整体思想是指从整体上去认识问题，思考问题，重点分析问题整体结构与特征，从而达到化繁为简、變难为易的目的。整体思想主要表现为整体思考、整体运算、整体代换或整体构造等，它可以应用在方程与不等式、函数与图象、几何与图形等诸多方面。以下笔者结合几则典例，重点探讨代数中的整体思想及其应用。

一、平方差公式中的整体思想

平方差公式用字母可表示为[（a+b）（a-b）=a2-b2]，公式里的字母[a]，[b]可以是单项式，也可以是多项式，当字母是多项式时，需要用整体思想加以处理，当算式需要多处应用平方差公式时，也需要用整体思想。

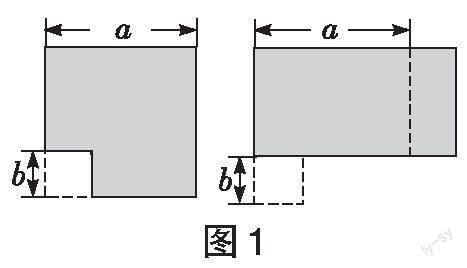
［例1］如图1，在边长为[a]的正方形中挖去一个边长为[b]的小正方形（[a>b]），把余下的部分剪拼成一个矩形。（1）通过计算两个图形的面积（阴影部分的面积），可以验证的等式是     。（请选择正确的一个）

A. [a2-2ab+b2=（a-b）2]

B. [a2-b2=（a+b）（a-b）]

C. [a+ab2=a（a+b）]

D. [a2+2ab+b2=（a+b）2]

（2）应用你从（1）选出的等式，完成下列各题：①已知[x2-4y2=12]，[x+2y=4]，求[x-2y]的值；②计算：（22+42+62+82+102+122+…1002）-（12+32+52+72+92+112+…+992）。

思路导引：（1）利用大正方形面积减去小正方形面积表示左图阴影部分面积，用长方形面积公式表示右图阴影部分面积，根据面积不变得到结论；（2）①运用平方差公式，将[x2-4y2=12]，[x+2y=4]整体代入求解；②算式是多个连续偶数的平方和减去多个连续奇数的平方和，利用加法的交换律与结合律变为若干个平方差的和，从而解决问题。

解：（1）左图中，阴影部分为大正方形减去小正方形，面积为[a2-b2]，右图阴影是拼成的长方形，长为[a+b]，宽为[a-b]，所以右图阴影部分面积为[（a+b）（a-b）]，由于左、右两图面积相等，所以[a2-b2=（a+b）（a-b）]，故答案为B。

（2）①由（1）中规律，利用平方差公式可得[x2-4y2=（x+2y）（x-2y）]，∵[x2-4y2=12]，[x+2y=4]，∴[x-2y=12÷4=3]。②通过观察，此题数字具有一定规律，可用运算定律将原式写成：（22-12）+（42-32）+（62-52）+（82-72）+…+（1002-992）=（2+1）（2-1）+（4+3）（4-3）+（6+5）（6-5）+（8+7）（8-7）+…+（100+99）（100-99）=3+7+11+15+…+199=1+2+3+4+5+6+7+8+…+99+100=（1+100）×（100÷2）=5050。

点评：当平方差公式的两个数分别是多项式时，计算时需要用整体思想。

二、完全平方公式中的整体思想

完全平方公式是指两数和或差的平方，等于两数的平方和加上或减去这两数积的2倍。反之，两数的平方和加上或减去这两数积的2倍，等于这两数和或差的平方。用字母可表示为[（a±b）2=a2±2ab+b2]，公式中的字母[a]，[b]可以表示单项式，也可以表示多项式，当字母表示多项式时，需要用整体思想来处理。

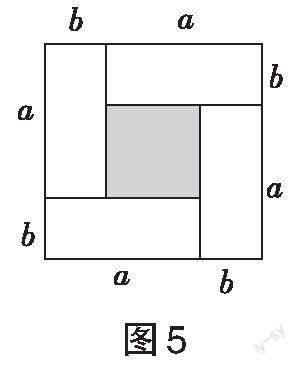
思路导引：（1）从正方形面积公式与大正方形的面积组合两个角度得到大正方形面积，根据面积相等，得到结论；（2）由（1）得到的公式，得[x]，[y]两数差、两数和与两数积的关系式，整体代入求值；（3）将完全平方公式变形，得到[2ab=（a+b）2-（a2+b2）]，然后整体代入求解。

解：（1）由正方形面积公式，得[S大正方形=（a+b）2]，由大正方形面积等于小正方形面积+四个矩形面积，得[S大正方形=（a-b）2+4ab]，∴[（a+b）2=（a-b）2+4ab]，故答案为[（a+b）2=（a-b）2+4ab]。

（2）由（1）可知[（a+b）2=（a-b）2+4ab]，得[（x-y）2=（x+y）2-4xy]，∴[（x-y）2=（x+y）2-4xy=16]，∴[x-y=±4]。

（3）∵[（a+b）2=a2+2ab+b2]，∴[2ab=（a+b）2-（a2+b2）]，∴[2（2020-m）（m-2023）=（2020-m）+（m-2023）2-（2020-m）2+（m-2023）2=（-3）2-7=2]，∴（2020-m）（m-2023）=1。

点评：在第（2）小题中，已知两数和与两数积，整体代入就可以求出两数的差，其关键是掌握两数和、两数差、两数积之间的计算公式；在第（3）小题中，已知两数的平方和求两数积，整体代入求解，其关键是将完全平方公式变形。

三、因式分解中的整体思想

因式分解是指将一个多项式分解为几个整式的乘积的形式，它的过程与整式乘法相反，因式分解的方法包括提公因式法、公式法、分组分解法、十字相乘法等，当公因式是多项式，需要整体将公因式提出来，当乘法公式里的字母表示多项式时，也需要用整体思想来处理。

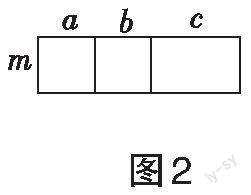
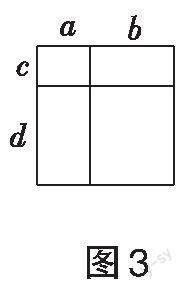
思路导引：（1）根据所给三个等式，发现结果均是一个二项式，x的指数比等式左边的最高次数大1，由此填空；（2）根据（1）的计算结果，将多项式m7+m6+m5+m4+m3+m2+m+1转化为两个多项式的相除，再被除数因式分解，约分后得到分解因式的结果；（3）与（2）的分解因式对照，（3）的算式相当于（2）的多项式，将[m=2]代入后可得a，b，c，d的值，最后再化简求值。

点评：从上面的解答可以看出，分解因式的方法可以从整式乘法里获得，将整式乘法反过来就是分解因式的结果。

四、二元一次方程组中的整体思想

解二元一次方程组的基本思想是消元，基本方法是代入消元法与加减消元法，其目的是将二元一次方程组化为一元一次方程来解。解二元一次方程组还有一种方法叫作整体代换法，它是将方程组中的某一部分看作一个整体，通过整体代换的方法消元，也可以达到解方程组的目的。

思路导引：（1）仿照材料中的“整体代换”解法，将[3x+5y]看作一个整体，将方程②变形后，把方程①整体代入解方程组；（2）①仿照材料中的“整体代换”解法，将[2x2-xy+3y2]看作一个整体，将方程②变形后，把方程①整体代入求得[xy]的值；②根据[xy]的值，列出[x]，[y]对应的整数值，再代入方程组进行检验。

点评：整体代换法就是一种整体代入的思想方法，适用于特殊的方程组。

五、分式方程中的整体思想

分式方程是指分母中含有未知数的方程，解分式方程的基本思想是化分式方程为整式方程，基本方法就是去分母。对于特殊类型的分式方程，可通过观察几个具体的方程的解从而获得规律，再根据规律求得同一类型的分式方程的解，此时需要用整体思想将非此类型的方程进行变形。

数学教育家波利亚指出，要将问题作为一个整体来理解，然后再判定哪个点是最重要的内容，这样就占据了有利的位置，没有整体理解问题就从细节开始，是一种愚蠢的做法。由此可见整体思想的重要性。以上笔者从五个方面探析了整体思想的运用，以期给读者一些体会与感悟。