“以退为进”教学实录

[一、创设情境，引入新课]

师：同学们，几千年来，龙一直是咱们中华民族的象征、中国文化的象征。每到重大节日，人们通常以舞龙相庆。老师所在的学校就有一支自己的轮滑舞龙队。（播放视频）你们想不想也置身其中体验一把？如果让你来选择，你选择舞龙的哪个部分？

很多学生选择舞龙头。

师：这么多人想舞龙头，可龙头只有一个呀，机会给谁呢？舞龙队的老师想出了一个与众不同的选拔方法。看，他是这样做的（课件出示）：

体育老师请全校舞龙队128名技术相当的同学围成一圈。从1号同学开始，每隔1人留下1人，也就是留下1号，去掉2号，留下3号，去掉4号……周而复始，谁是最后留下的谁就去舞龙头。

教师随机挑选7名学生来讲台前演示。

师：活动开始前，大家先猜猜，谁会是最后的幸运者呢？

学生争论不休。

师：我们看看实际的结果吧！开始。

学生按照选拔方法演示，发现最后剩下的是7号。

设计意图：课的开始，增强学生的民族自豪感并进一步聚焦数学问题，再让学生亲身演示，分层理解复杂的方法，降低学生研究难度的同时激发学生研究的内驱力。

[二、以退为进，研究规律]

师：舞龙队有128人，按照这个方法选拔，最后剩下的是几号呢？

生1：128号，因为刚才7人时剩下的就是最大的。

生2：肯定不是128号，因为双数肯定会被去掉。我猜应该是127号，那是最大的单数。

……

师：同学们都有自己的分析和猜想。正所谓“实践出真知”。下面请打开1号学习单，这里从1开始的128个连续自然数代表128个人的号码。给大家2分钟时间，请自己找找看。

学生动手尝试

师：大家找到结果了吗？

生：没有。时间太短，数太大，找着找着就乱了。

师：那你们打算怎样研究？

生：选择较小的数试试。

生：不能只选1个数，用连续的、较小的数尝试几次，就容易发现规律了。

师：很好！你们和我国著名的数学家华罗庚先生想的一样。他曾经说过，善于退，足够的退，退到原始而不失重要性的地方，是学好数学的一个诀窍。看来大家都具有与数学家相似的思维方式！当我们遇到困难问题时，不妨先策略性地退一退，退下来再研究，规律也就容易发现了。（板书：退）

师：大家觉得把128这个数退到几进行研究比较合适呢？

生：退到一半，64。

生：退到10。

师：能退得更彻底点儿吗？

生：退到1。

师：只研究1人时的情况吗？

生：需要研究从1开始的连续自然数，看看有没有规律。

师：方法清晰了，下面就请大家以从1开始的较小数为例进行研究。

教师出示研究建议：

1.小组合作进行研究，并将研究结果填在表中。

2.观察多少人时从1号开始按规律选，最后还剩1号。

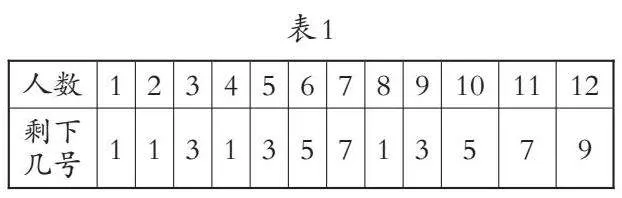
学生自主开展研究并汇报，教师将结果填在表1中。

师：我们一起来看看表1，多少人的时候，最后剩下1号？

生：人数是2的倍数时最后剩下的是1号。

生：不对，6也是2的倍数，最后剩下的就不是1号。

生：我发现当人数是从1开始连续乘2的数时，最后剩下的就是1号。

师：他发现的规律对吗？如果按照他说的规律，下一个最后剩下1号的人数将是——

生：16。

师：对吗？我们一起试试看。

学生自主验证，发现人数是16时最后剩下的是1号。

师：像1、2、4、8、16这样从1开始连续乘2的数叫什么数呢？

生：我听说过，好像叫2的次方数。

师：你的知识真渊博。就像他说的，数学中我们把像这样由若干个2相乘得到的数叫2的n次方数，其中1是2的0次方。（板书：2的n次方数）

师：现在大家明白规律了吗？谁能总结一下？

生：当人数为2的n次方数时，最后剩下的是1号。

设计意图：在此环节的教学过程中，教师积极引导学生通过实际操作，将个体意见汇聚成群体共识，再通过对数据的整体分析获取初步的规律性结论，使学生掌握“退”的数学方法，感悟其背后的数学思想。

[三、深入探索，理解本质]

师：研究到这里，你们满意了吗？

生：不满意，为什么会有这样的规律呢？

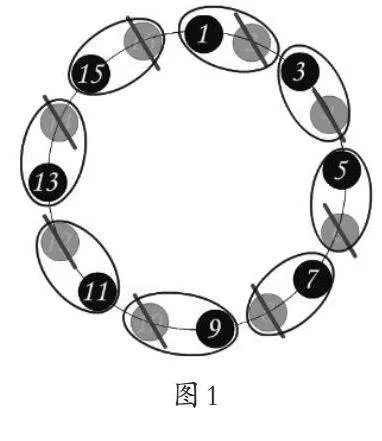
师：大家真有研究的意识，不但发现了规律，还想研究规律背后的原理。让我们结合刚才的研究，以16人为例，看看有16人时1号究竟是如何被留下来的。

生：16人时正好可以2人一组，每次画去的是每组的后一人，所以最后一组的最后一人，也就是1前面的数会被画掉，1会被保留下来（如图1）。以此类推，最后只剩下1号。

师：为什么1总能被留下来呢？

生：因为16是偶数，而且每次除以2后还是偶数，这样就总可以2人一组，每次画掉的是每组的后一人，1作为第一组第一个会被一直留下来。

师：128人时为什么最后剩下的是1号，你能说明了吗？

生：因为128是2的7次方，而且每次除以2后还是偶数，这样就总可以2人一组，每次去掉的是每组的后一人，1作为第一组第一个就会被一直留下来。

生：人数只要是2的n次方数，按规则画，每圈都可以正好2个数为一组，画去的总是每组的后一个数，1前面的数总会被画掉，而1不受影响，最后剩下1号。

师：回顾一下刚才研究的过程，我们通过怎样的研究得到了这个了不起的结论？

生：我们先从较大数退到较小数再进行研究，进而发现规律。

师：这样看来，“退”是方法，其目的是更好地“进”，这在兵法上叫作“以退为进”。老师为你们今天的研究成果感到高兴，你们真了不起。

设计意图：教师进一步引导学生透过现象分析、揭示背后的本质原理，有效提升学生的抽象、推理和建模素养。

[四、分层练习，深化理解]

师：同学们，规律大家已经掌握了，现在请应用规律解决一些实际问题。

问题1：五年级32个同学在操场上围成一圈，玩报数游戏，从1号开始，每隔1个去掉1个，即留下1号，去掉2号，留下3号，去掉4号……周而复始，最后剩下的是几号？为什么？

问题2：还是这32个同学，仍然按照刚才的规则报数（每隔1个去掉1个）。聪聪是5号，结果他是最后留下的人，这是怎么回事呢？

问题3：五年级（1）（2）两个班共64个同学在操场上围成一圈，玩报数游戏，从1号开始，每隔1个去掉1个，即留下1号，去掉2号，留下9zPUlSHk2dWhC9WHQ5LkcsBuNQWPvLiZId3FuWvNAns=3号，去掉4号……周而复始，最后剩下的是几号？

问题4：迪迪提议改变一下规则，还是32个同学，每隔1个留下1个，即去掉1号，留下2号，去掉3号，留下4号……周而复始，最后剩下的是几号？

师生逐一解决问题。

设计意图：教师分层设计练习活动，并在练习过程中将学生对“退”的认识加以拓展，从“数大小”的“退”，发展到“方法本身”的迁移上来，进一步丰富学生的方法性体验，开阔学生的思维。

[五、全课总结，升华认识]

师：课上完了，今天这节课你们有什么收获？

生：我学会了一种思考问题的方法。

师：你还有什么不清楚或遗憾的地方吗？

生：如果人数不是2的n次方数，又该如何解决呢？

教师出示问题：

五年级129个同学在操场上围成一圈，玩报数游戏，从1号开始，每隔1个去掉1个，即留下1号，去掉2号，留下3号，去掉4号……周而复始，最后剩下的是几号？

师：请同学们下课后继续研究吧！

设计意图：思维的发展不能因为课的结束而终结。在此环节中，教师进一步引导学生从方法论的角度进行思考，感受数学方法、数学思想内涵价值的同时，延伸学生对问题的思考热度，真正实现“课终结而思维不止”的育人目标。

【本文系北京市教育科学“十四五”规划2021年度一般课题“以数学为主导的多元学科整合课程的开发与实践研究”（编号：CDDB21229）的研究成果】

（作者单位：北京市东城区府学胡同小学，北京师范大学课程与教学研究院）