多元表征视角下小数意义的教学设计

多元表征是指用多种形式表征同一个学习对象。在数学教学中合理运用多元表征，有助于学生深刻理解数学概念，把握知识的本质。当前教学中经常出现因缺乏多元表征的学习过程，导致学生产生困惑或机械操练的现象。下面以“小数的意义”为例，从教学中存在的问题、原因分析及改进策略三个方面谈一谈多元表征视角下小数意义的教学设计。

[片段一：] [一、存在的问题]

小数知识的学习过程中，以下问题屡见不鲜。

问题一：小数的学习中避不开的一个问题就是，小数分为整数部分和小数部分，小数部分到底指的是什么？例如，6.75的小数部分是75还是0.75？如果是75，有的学生就产生疑惑了：小数部分应该是小数才对，怎么会是整数呢？如果是0.75，又有学生疑惑了，那写成原数岂不是6.0.75？

问题二：试卷上常常出现这样的题目，也往往会引起学生的争论——0.25×1.4的积是（ ）位小数。不少教师往往会提醒学生谨慎答题，不要“上当”，一定要计算出结果化简以后再看积是几位小数。还有诸如此类的判断题：两位小数乘一位小数，积一定是三位小数。每到此时，学生和老师都异常纠结。

问题三：在学习了小数的性质之后，一道这样的练习题成了“理所应当”：把0.4改写成用0.001作单位的数是（0.400）。若联想到把0.3元改写成用“角”作单位是3角，把50000改写成用“万”作单位的数是5万，再想想前面那道题，会不会感觉到一丝异样？

问题四：笔者参加一次赛课，课题是“小数乘10、100、1000……的计算规律”，完整的情境，流畅的过程，活跃的氛围，与旧知串联从而形成知识框架……都让笔者感觉会有一个很好的结果。结果，评委给出的结论却是教学内容过于简单，即仅仅只是通过观察归纳“一个小数乘10、100、1000……只要把这个小数的小数点向右移动一位、两位、三位……”过于肤浅。

笔者当时陷入了极度的困惑中，也正因此，结合以上问题开始思考：小数的教学到底要教什么？如何教？教到什么程度？

[片段一：] [二、原因分析]

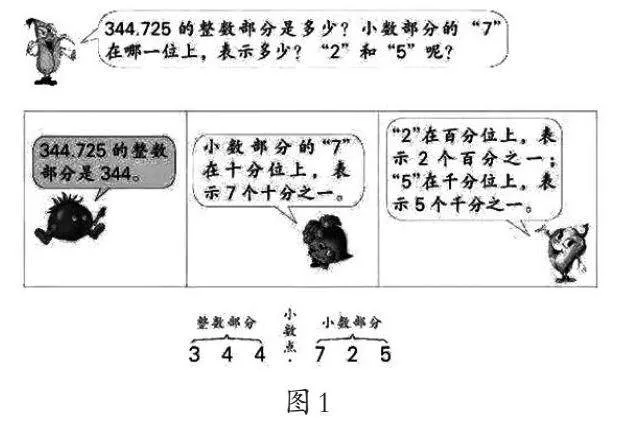
上述问题一，我们在教材中就可以找到答案（如图1），且这里说的小数部分指的是计数单位的个数，由此6.75的小数部分就是75，表示有75个最小计数单位，即75个0.01。

上述问题二，2022年版课标指出，对小学阶段“数与运算”主题，在理解整数、小数、分数意义的同时，理解整数、小数、分数基于计数单位表达的一致性。这里的“基于计数单位表达的一致性”不仅包括这些数都是计数单位的个数的累加，也包括这些数的运算都是计数单位的个数的运算。由此，计算0.25×1.4实际上是在计算（25×14）个（0.01×0.1），即最小计数单位0.001的个数，从这个意义上判断，0.25×1.4的积应该是三位小数，进而可知，确定积的小数位数，实际上是在确定计算中产生的新的最小计数单位。

上述问题三，0.4实际上是用“一”做单位的，表示“一”的十分之四或0.4个“一”，如果要改成用0.1做单位，那就可以数出4个0.1，即4；改成用0.001做单位，那就可以数出400个0.001，即400。这就好像50000表示50000个一，改写成用“万”做单位，是5个万，即5万；0.3元是0.3个1元，改写成用“角”做单位是3个1角，即3角。所以把0.4改写成用0.001做单位的数是（400）而不是（0.400）。

上述问题四，通过观察归纳得出“小数乘10、100、1000……的计算规律”，学生就只是在模仿规律进行计算，不能解释规律背后的道理，是对数的意义核心理解的缺失。建立“数”的意义的四个要素分别是数位、计数单位、位值、十进制，小数乘10、100、1000……实则是把计数单位扩大到原来的10倍、100倍、1000倍……小数点的移动实际上是在十进制的法则下扩大计数单位。

综上，造成上述问题的根本原因是对“单位”理解的肤浅和偏差，要想深刻理解“单位”，就需要在小数意义的教学过程中引导学生进行多元表征，多元表征的过程有利于学生深刻理解数的本质、小数的意义，上述问题也就迎刃而解了。以往或者当前的一些课堂教学中也能够看到表征的过程，但是一方面表征不多，不足以让学生从不同的表征中发现相通的地方，突出知识的本质；另一方面表征虽多，但缺乏带有学生个体色彩的表征方式，即缺乏开放性，未能激发学生学习的自主性和创造性。

[片段一：] [三、改进策略]

苏教版教材五年级上册第三单元主要包括小数的意义和性质两大块内容，而小数的性质是基于小数的意义生长的，小数的意义实则包含两方面：一是意义，即平均分的意义，与分数紧密联系；二是形式，即十进制表达形式，与整数紧密联系。在小数意义的教学设计中，利用多元表征，充分感悟计数单位及计数单位的个数，既有助于基本性质的学习和运用，也有利于打通整数、分数和小数之间的联系，体现数和运算基于计数单位表达的一致性。

1.注重小数意义表征的多元化。

多元表征视角下，小数意义的教学设计可以分为“小数的意义”和“小数的数位意义”两课时，“小数的意义”主要从小数平均分的意义角度对小数进行表征，“小数的数位意义”主要从小数的表达形式角度对小数进行表征，均注重表征的多元化。在“小数的意义”教学中，设计了三大任务，并在完成任务过程中进行多元表征：一是在不同的地方寻找[1100]，二是用不同的方式表示0.06，三是用不同的方式说明0.6与0.06的大小关系。

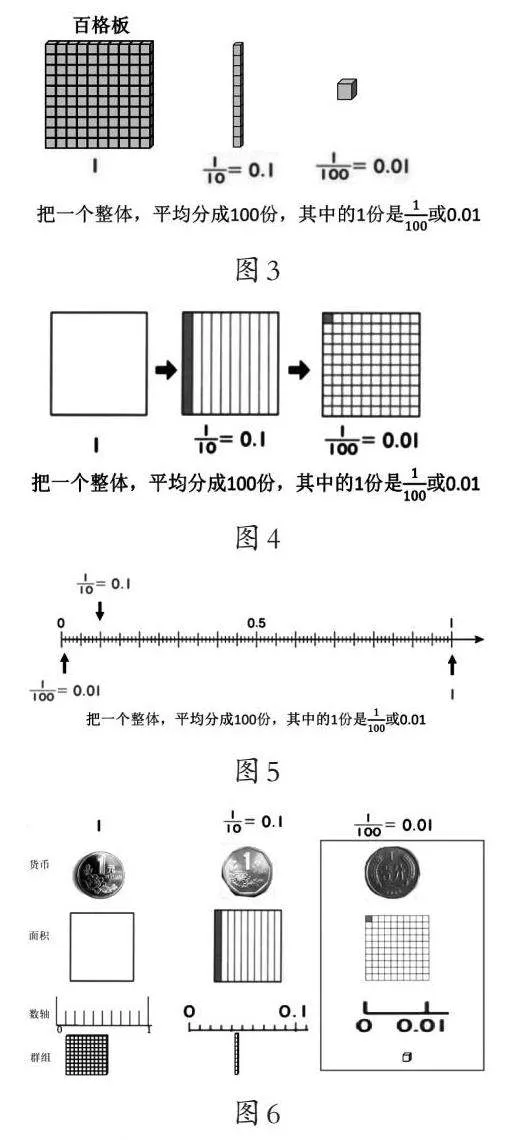
在第一个任务中（活动一），笔者设计了如下多元表征：货币（如图2）、群组（如图3）、面积（如图4）、数轴（如图5），最后把多元表征汇总在一起（如图6），沟通不同表征之间的联系，突出0.01的本质，即把一个整体平均分成100份，其中的1份就是[1100]或0.01。

以上设计通过寻找0.01的过程（实际上也包括寻找1和0.1），在多元表征中不断强调平均分意义，将0.01与平均分意义联结，既是认识两位小数的开端，也是理解两位小数的基础，所有的两位小数都是在数几个0.01，突出了0.01是两位小数的最小计数单位。

2.注重小数意义表征的开放性。

有了0.01的多元表征和意义做基础，第二个任务用不同方式表示0.06，则注重鼓励学生结合刚才的学习体验，独立表征0.06并交流展示。

活动二：用不同的方式表示0.06。

活动要求：

（1）独立思考，每人至少选择一种方式表示0.06，也期待你思考其他方式。

（2）小组内交流不同的表示方式。

学生除运用货币、群组、面积、数轴进行表征以外，还想到了画100个点圈起来表示1，再在其中圈6个点来表示这100个点的0.06；想到了看一本书，把这本书的页数平均分成100份，看了其中的6份，是0.06本；想到了妈妈的一支口红，平均分100天用完，6天就用了0.06支；想到了把一个蛋糕平均分成100份，其中的6份就是0.06个蛋糕……

这个活动可以帮助学生巩固对小数意义的理解，明晰1、0.1、0.01三个计数单位的对照物，沟通0.06与0.01之间的关系，即6个0.01，熟练进行小数与表征类型之间的转化。这一活动让学生自主进行，不仅检验他们对小数的理解情况，也能让学生在不断地探究活动中，体会不同表征下的小数，以加深对小数的综合认识；并不断体会小数与分数以及整数的联系，增加对数的整体宏观认识。如此让表征从“多元”走向“开放”，是对“多元表征”另一种方式的回归。

活动三：用不同的方式说明0.6和0.06的大小关系。

这个探究活动让学生延续刚才对0.06的表征，继续表征0.6，从而发现0.6和0.06的大小关系，进一步体会各个符号的含义，感悟用来表示数的标准，即最小计数单位，以及计数单位的个数。

后面三位小数的学习便可在此基础上引导学生利用多元表征自主学习和探究。在多元表征下，学生充分理解了小数的平均分意义，那么在第二课时学习“小数的数位意义”，认识数位、计数单位、位值、十进制时，就有了依靠和支撑。

综上所述，多元表征贯穿了小数意义学习的整个过程，是小数知识的载体，也是学生探究小数知识的工具，通过各种表征与小数的联结，学生才能深刻理解和掌握小数的后续相关知识，也才能在遇到类似上述四种问题的时候，不纠结、不迷茫，并能坚定地作出回应。同时教学设计中要注意多元表征的多样性和开放性，老师在引导学生进行多样化表征的同时，也要给予学生“多样”之外用属于学生自己的方式进行表征的空间和时间。

（作者单位：南京师范大学苏州实验学校）