“小数的意义和加减法”单元整体设计

通过问题提出开展教学是当前数学教育研究领域的一个热点，尽管越来越多的教学实践引进了问题提出活动，但对于课堂教学中如何通过设计问题提出任务，促进学生的数学学习，还缺乏足够的研究。本文针对“小数的意义和加减法”单元开展了问题提出任务的整体设计，以促进学生深入理解小数的意义及加减法的运算道理。

一、“小数的意义和加减法”单元分析

本单元是在初步认识小数的基础上学习的，主要目的是进一步理解小数的意义，并在加减法中应用小数的意义，体现数的认识和运算的一致性。

1.数学分析。

小数的意义是由分数与整数概念统整建立起来的。当出现了比单位“1”更小的数量时，需要将“1”继续等分进行表达，从这个意义上说，小数（有限小数和循环小数）是十进分数的另一种表达，。另一方面，张奠宙教授指出：“小数是一种特殊的分数，但是又独立于分数……小数的出现，是基于十进制表示数量的需要。”从这个意义上说，小数和整数紧密联系，可以看成是整数十进位值制计数法反向延伸的结果。进一步，利用对小数计数单位的理解，可以得到小数加减法运算的道理：都是在相同计数单位下进行。而从现实生活中的数量抽象出小数，将小数还原到现实生活中的数量，体现了学生数感的发展；将整数十进位值制计数法迁移到小数，并在此基础上进行比较大小和加减法计算，则体现了学生推理意识和运算能力的发展。

2.认知分析。

生活中的人民币模型、长度模型等，为学生理解小数提供了丰富的直观支撑。分数表示的部分与整体的关系，以及整数的十进位值制表达和运算为理解小数的意义和运算奠定了基础。这都是学生学习小数的意义和加减法的前经验。但学生对小数的学习有不少的困难和误解，主要表现如下：

第一，对于整数或分数知识“过度类推”而产生误解。一方面，瑞思尼克（Resinick）等人提出学生可能犯“分数规则”的错误，将分数所切割的份数大小与数目观念应用到小数所代表的指示物上，认为百分之一比十分之一所代表的份数小，从而推论两位小数比一位小数小，比如0.68小于0.5。另一方面，有些学生认为3.21大于3.8，因为21大于8。这是因为他们忽视小数点的存在，而把小数当作整数来处理，瑞思尼克将这类错误称为“整数规则”错误。“整数规则”还可能造成学生在小数读法上的困惑：3.21为什么要读成三点二一而不是三点二十一？在小数的数位上，有的学生也会受整数数位的影响，对小数部分进行“对称性”的反向延伸，将小数部分从左往右依次命名为“个分位”“十分位”……有的学生则将0.8、0.9的下一个数写成0.10。

第二，由于小数和分数的表征系统不同，一个单位被等分为多少，在分数的分母中是明确表示出来的，而小数中一个单位被等分为多少隐含在数位系统中，因此造成学生在进行分数和小数转换中出现错误，如学生将0.5写成[15]，3.4写成[34]。

第三，对于0.1千克、0.1平方米、0.1时等现实数量，由于有的学生只将小数点作为单位分割的标志，而忽略了表达数量的单位之间的关系，从而出现错误：0.1千克表示的是1克，0.1平方米表示的是1平方分米，0.1时表示的是1分钟。

第四，有的学生不理解小数点的作用，仅把它作为单位的分割符号或者将“0”与其之外的数字隔开，如将1分写成0.0.1元，将[1100]写成000.1。

3.教学分析。

本单元有三个重要的学习任务：从数量中抽象出小数、十进位值系统的自然延伸、应用数位进行大小比较和加减法运算。学生的学习活动应据此进行整体设计。

学生将尝试解读0.1千克、0.1平方米、0.1时等数量的实际意义，虽然学生在解读的过程中可能产生困难，但根据小数与十进分数的关系来准确解读这些数量的实际意义，有助于学生更好地理解小数的意义。

学生将实现知识迁移，这体现在将整数位值系统迁移到小数位值系统，以及将整数比较大小、加减运算的道理迁移到小数中。

二、单元学习目标及问题提出活动的整体设计

1.单元学习目标。

根据以上分析，本单元的学习目标为：

（1）经历刻画测量结果从而产生小数的过程，体会小数可以表示现实生活中比1小的数量，感受小数与日常生活的密切联系。

（2）能解读人民币、长度、质量、面积、时间等的具体数量的实际意义，在此基础上抽象出小数，认识小数可以表示十进分数。

（3）能利用方格图、数线等直观模型表示小数，会进行十进分数与小数的互化。

（4）经历创造小数数位的过程，借助整数十进位值系统的经验认识小数的数位，掌握小数数位顺序表，认识小数各数位的计数单位及其关系。

（5）根据对小数数位的理解探索如何比较大小和进行加减法运算，会进行小数比较大小和加减法运算。

2.单元整体学习活动设计。

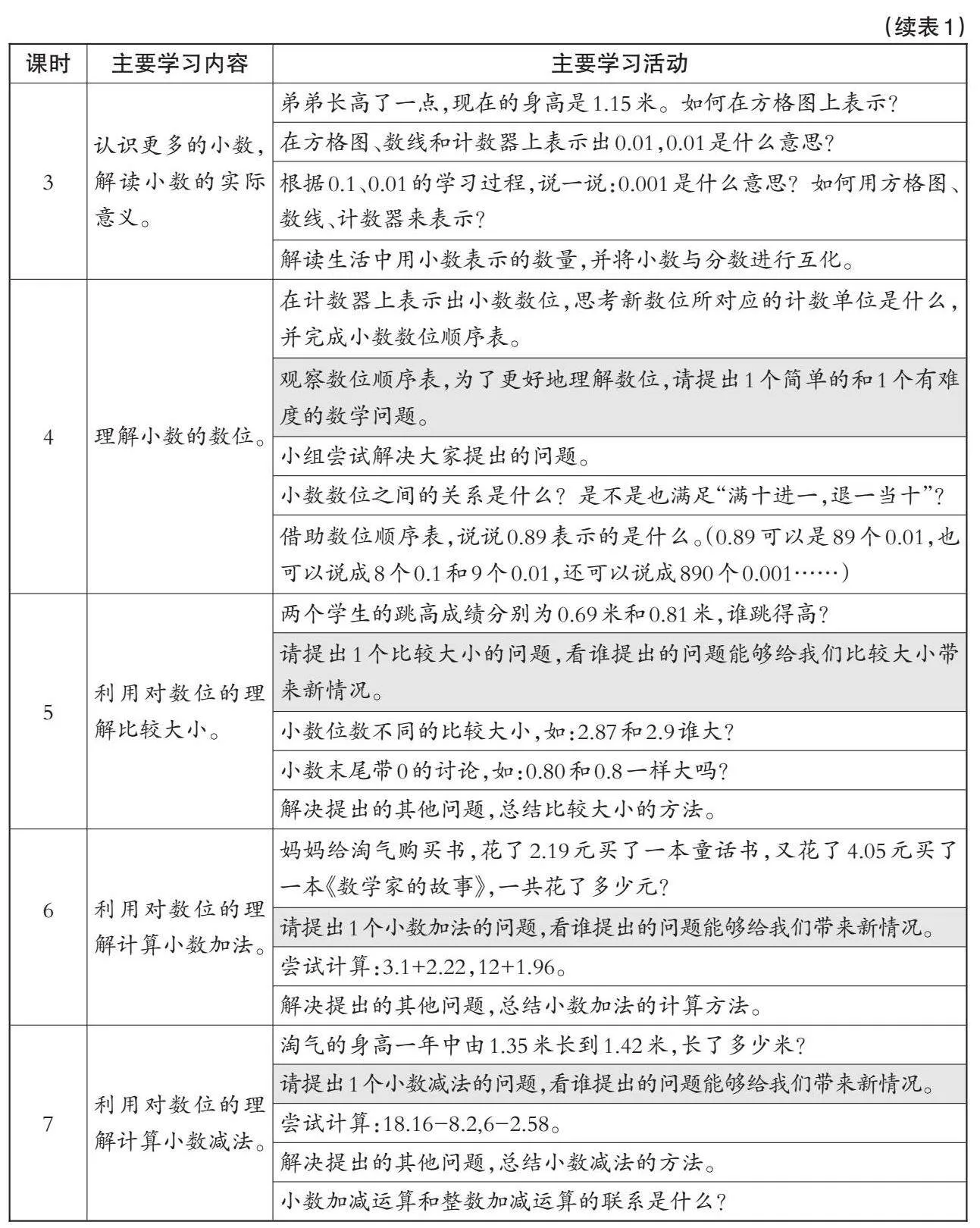
本单元整体学习活动设计（不含小数加减混合运算）如表1所示，阴影处是设计的问题提出活动。

需要说明的是，表1中的课时划分只是参考，其中没有包括教材中设计的单元练习时间、整理与复习的时间，教师可以在教学中根据实际情况进行调整。同时，问题提出活动的设计是围绕前面的三个学习任务设计的。

三、问题提出活动的具体设计

1.从数量中抽象出小数过程中的问题提出活动。

首先，鼓励学生思考如何将1分米表示为以米为单位的数，这既体现了小数产生的必要性，也唤醒了学生的学习经验，学生不难得到0.1米。

为了将0.1米与十进分数建立联系，鼓励学生在方格图和数线上表征0.1米，感受0.1米是将1米平均分成了10份，取其中的1份（如图1）。

接着，继续解读生活中的小数表示的其他数量，如0.1千克、0.1平方米、0.1时，并借助方格图、数线对它们进行表征。尽管学生容易只将小数点作为单位分割的标志，而忽略单位之间的关系，常常认为0.1千克表示的是1克、0.1平方米表示的是1平方分米、0.1时表示的是1分钟，但借助0.1米的表征过程，学生将认识到它们分别是将1千克、1平方米、1时平均分成了10份，取其中的1份。

最后，鼓励学生观察这些不同的数量，提出1个值得继续思考的数学问题。学生可能提出“这些例子的共同点是什么？为什么都可以用0.1来表示”“0.1到底代表什么含义”“0.1还可以表示什么”等问题。这些问题都体现了从数量中抽象出数、将数还原成数量的过程。

2.从整数数位迁移到小数数位的问题提出活动。

在认识了小数和十进分数的关系后，鼓励学生在计数器上表示出小数数位，完成小数的数位顺序表（如图2）。

此时，鼓励学生在计数器上拨珠子，以及观察数位顺序表。为了更好地理解数位，可以引导学生每人分别提出1个简单的和1个有难度的数学问题。学生可能提出的简单问题有：“几个0.1是1？”“百分位和千分位是什么关系？”可能提出的有难度的问题有：“十分位和千分位是什么关系？”“相邻计数单位的关系是什么？”“整数数位关系和小数数位关系的相同点是什么？”“小数部分万分位后面的数位是什么？”这些问题都体现了学生对数位及其关系的理解。

3.利用数位理解比较大小的问题提出活动。

在学生理解小数数位的基础上，鼓励他们尝试进行两位小数的比较大小，如0.69米和0.81米。学生此时虽然能够比较大小，但由于小数的数位相同，学生很难意识到数位的重要性。

正如前文所提到的，当小数的数位不同时，学生会犯“分数规则”或“整数规则”的错误。此时，可以鼓励学生提出1个小数比较大小的问题，提出的问题能够给大家带来新情况。他们需要思考小数比较大小的道理是什么，和刚才的例子比较会出现什么新情况。为此，他们可能会提出小数位数不相同的数如何比较大小，如：2.87和2.9谁大？或者小数末尾带0的问题，如：0.80和0.8一样大吗？这些问题都体现了学生对小数比较大小道理的理解。

4.利用数位理解进行加减法的问题提出活动。

在学生理解了小数数位的基础上，鼓励他们尝试进行两位小数的加减法运算，并利用问题提出活动鼓励学生主动思考，提出1个小数加法和减法的问题，能够给大家带来新的思考。学生可能会提出小数位数不相同的数如何加减、整数如何减去一个小数等问题，这些问题能够促进学生对小数加减法运算道理的理解。

（作者单位：浙江杭州市临安区衣锦小学）