为提升学生的思维力而教

“数学是研究数量关系和空间形式的科学。”史宁中教授认为，数学的研究对象包含数量与数量关系、图形与图形关系，研究数量之间和图形之间的关系比数量和图形更重要。小学数学中有很多研究规律的内容，本质上就是研究数量之间和图形之间的关系。

“商不变的规律”是四则运算的一个重要规律，有些老师教学时止步于引导学生了解什么是“商不变的规律”、怎样推导“商不变的规律”及应用“商不变的规律”，这样教学使学生对“商不变的规律”的认识停留在知识层面，没有触及“商不变的规律”的本质，学生对为什么“被除数和除数同时乘或者除以一个相同的数（0除外），商不变”不甚了解，因此可以在学生认识“商不变的规律”的基础上，专门安排一节思维训练课，围绕问题带领学生研究“商不变的规律”背后的秘密，揭示“商不变的规律”的本质。

一、回顾：寻找教学的起点

教师引导学生回顾什么是“商不变的规律”，是怎样研究“商不变的规律”的。

生：在除法中，被除数和除数同时乘或除以一个相同的数（0除外），商不变，叫作商不变的规律。

生：我们先比较除法算式之间的关系提出猜想，然后举例验证得出结论，从而发现规律。

师：请看大屏幕，仔细观察每个算式，先说说被除数和除数分别是怎样变化的，再直接说出第二个、第三个算式的商。

200÷40=5

40÷8=

400÷80=

生：40÷8和200÷40相比，被除数和除数同时除以相同的数5，商不变；400÷80和200÷40相比，被除数和除数同时乘相同的数2，商不变。

生：还可以这样想，400÷80和40÷8相比，被除数和除数同时乘10，商不变。

师：这真是变中有不变啊！根据除法算式之间的关系，应用商不变的规律，可以使一些计算简便。

思考：美国著名教育心理学家奥苏贝尔曾说过：“如果我不得不将教育心理还原为一条原理的话，我将会说，影响学习最重要的原因是学生已经知道了什么。”教学是基于原有知识水平和思维水平的有限延伸，首先要找到教学的起点，“商不变规律的再认识”是在学习“商不变的规律”知识基础上的再认识，毫无疑问“商不变的规律”是教学的起点。因此，课始引导学生复习“商不变的规律”，并再次体会“商不变的规律”的价值。

二、思辨：引导学生发现问题

师：请同学们把“商不变的规律”再读一读，想一想能提出什么问题。

生：被除数和除数为什么要同时乘或除以一个相同的数？

生：相同的数可以是哪些数？

生：既然有“商不变的规律”，有没有“积不变的规律”“和不变的规律”“差不变的规律”？

师：刚才大家提出了三个非常有价值的问题，我们就围绕这三个问题走进“商不变的规律”的背后，开始今天的研究。

出示课题：“商不变的规律”的再认识。

思考：2022年版课标总目标中指出：“体会数学知识之间、数学与其他学科之间、数学与生活之间的联系，在探索真实情境所蕴含的关系中，发现问题和提出问题，运用数学和其他学科的知识与方法分析问题和解决问题（即‘四能’）。”教学中，要培养学生对已经掌握的知识大胆质疑的意识，用问题驱动学生思维。教师引导学生重读“商不变的规律”，基于原有认知，抓住“商不变的规律”的关键提出问题，这些问题源于学生思维的困惑，直指知识本质，由“商不变的规律”的表面走向背后，分析并解决这些问题，可以发展学生的问题意识，帮助学生掌握思维方法，提高学生的思维能力。

三、探究：揭开规律背后的秘密

1.为什么要同时乘或除以一个相同的数？

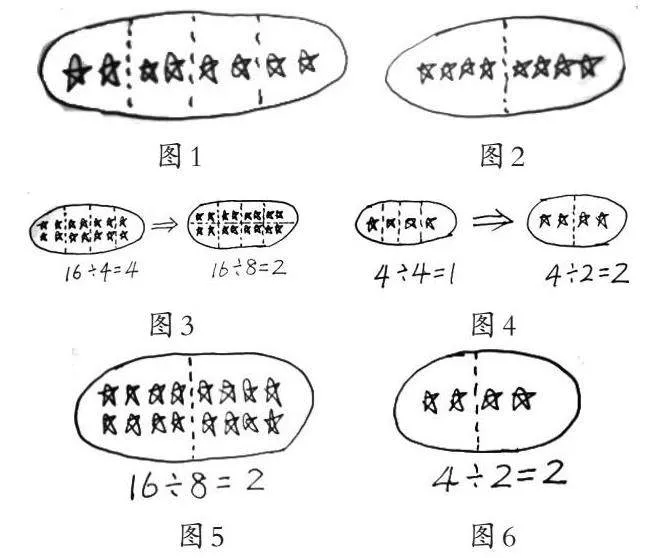
师：我们先来看第一个问题，被除数和除数为什么要同时乘或者除以一个相同的数？以除法算式8÷4=2为例，请大家画一画、想一想、说一说这个除法算式以及这个除法算式各部分表示的含义。

生：表示把8平均分成4份，每份是2。（如图1）8是总数，4是平均分成的份数，2是每份数。

生：还可以表示8里面有2个4。（如图2）把8看成总数，4表示每份数，2表示份数。

师：这个除法算式表示的这两种意义有什么相同点？

生：都表示平均分。

师：同学们，你们能利用这个算式，通过画图来说明为什么要同时乘或者除以一个相同的数吗？想一想，画一画，在小组内交流一下。

生：以图1为例，被除数乘2，总数变成16，如果除数不变，也就是平均分的份数不变，每份数就变成了4；要使每份数不变，平均分的份数也要乘2，把16平均分成8份，每份数还是2。这就是被除数和除数为什么要同时乘一个相同的数。（如图3）

生：还以图1为例，被除数除以2，如果平均分的份数不变，每份数就变成了1，要想每份数不变，平均分的份数也要除以2，把4平均分成2份，每份还是2。这就是被除数和除数为什么要同时除以一个相同的数。（如图4）

生：以图2为例，被除数乘2，总数变成16，要使份数不变，每份数也要乘2，每份数变成8。这就是被除数和除数为什么要同时乘一个相同的数。（如图5）

生：还以图2为例，被除数除以2，总数变成4，要想份数不变，每份数也要除以2，每份数变成了2。这就是被除数和除数为什么要同时除以一个相同的数。（如图6）

师：同学们真了不起，从两个不同的角度，借助画图说明了被除数和除数为什么要同时乘或者除以一个相同的数。

思考：学生借助画图，根据除法的意义，从两个维度直观形象地研究了“商不变的规律”中被除数和除数为什么要同时乘或除以一个相同的数，从规律的知识表面走向深刻内涵，揭开了“商不变的规律”的神秘面纱，让学生感受“商不变的规律”的本质。亦即，当总数乘或除以一个数时，要使每份数不变，平均分的份数也要乘或除以相同的数；或者，当总数乘或除以一个数时，要使份数不变，每份数也要乘或除以相同的数。

2.相同的数还可以是什么数？

师：我们已经知道相同的数可以是不为0的整数，请同学们猜想一下，还可以是什么数？

生：我猜想还可能是分数。

生：我猜想也可能是小数。

师：大家的猜想是否正确呢？小数乘除法和分数乘除法我们还没有学过，感兴趣的同学可以查阅资料，了解相关知识来验证我们的猜想。

思考：虽然此时学生还没有学习小数乘除法和分数乘除法，但是依然应该基于知识的整体让学生大胆提出猜想，发展学生的想象能力，培养学生的整体思维能力。

3.还有什么规律？

师：通过研究我们发现了“商不变的规律”，刚才同学们还提出有没有“积不变的规律”“和不变的规律”“差不变的规律”？请四人小组任意选一个问题，按照研究要求，合作研究。

研究要求：

①想一想，要使结果不变，算式中的两个数应该怎样变化？

②说一说，让小组其他同学明白你的想法。

生：我们组研究了“积不变的规律”，两个数相乘，一个乘数乘几，另一个乘数除以相同的数（0除外），积不变。

生：我想举例说明我们的想法。例如：2×4=8，表示4个2是8，第一个乘数乘2，如果第二个乘数不变，积就变成了16；要使积不变，第二个乘数就要除以2，算式是4×2=8，表示2个4是8。

师：哪个小组继续汇报？

生：我们组研究了“和不变的规律”，两个数相加，一个加数增加，另一个加数减少相同的数，和不变。例如：4+6=10，第一个加数增加2，如果另一个加数不变，和就增加了2，要使和不变，另一个加数就要减少2。

生：我们组研究了“差不变的规律”，两个数相减，被减数增加或者减少，减数也增加或者减少相同的数，差不变。例如：6-4=2，被减数增加2，减数不变，差就增加了2，要使差不变，减数也要增加2。

生：我们组发现“和不变的规律”“差不变的规律”中的“相同的数”可以是0。

思考：有了“商不变的规律”的研究经验和方法，学生研究其他三个规律就变得轻松自如。对于“积不变的规律”“和不变的规律”“差不变的规律”，虽然教材中没有安排专门课时教学，但是在实际教学中相关规律均有所涉及，此处把这三个规律提取出来，把教材进行整合集中研究，有利于引导学生对四则运算的相关规律的整体性认知，有利于提高学生的数学探究能力，有利于学生形成结构化的思维。

四、比较：沟通规律之间的联系

师：数学知识之间存在相似和相反两种关系。通过研究，我们发现了和、差、积、商不变的规律，比较这四个规律，你能说一说它们之间的关系吗？想好后在小组内交流。

生：“和不变的规律”和“积不变的规律”相似，“商不变的规律”和“差不变的规律”相似。

生：“和不变的规律”和“差不变的规律”相反，“积不变的规律”和“商不变的规律”相反。

师：同学们的发现能力太强了，大家能说一说理由吗？

生：因为乘法是求几个相同加数的和的简便运算，除法是求一个数连续减去几个相同数的差的简便运算，所以“和不变的规律”和“积不变的规律”相似，“商不变的规律”和“差不变的规律”相似。

生：因为减法是加法的逆运算，除法是乘法的逆运算，所以“和不变的规律”和“差不变的规律”相反，“商不变的规律”和“积不变的规律”相反。

师：真会思考！刚才有同学的一句话说得特别好，谁能把它重复一遍？

生：除法是求一个数连续减去几个相同数的差的简便运算。

师：这个同学用简洁的语言概括了除法和减法的关系，太了不起了。当我们对所学的知识有了较为深刻的理解后，就会发现数学知识之间存在千丝万缕的联系。

思考：数学教学不仅要引导学生掌握知识，更重要的是引导学生抓住知识的本质，根据知识之间的内在联系帮助学生建构数学知识的整体结构。

（作者单位：江苏沭阳县第一实验小学）