革命根据地教科书中的圆面积计算教学法及其启示

面积计算是小学数学中唯一的曲线图形面积计算教学内容。现行教科书一般是把一个圆分成若干等份，然后拼成一个近似的长方形或平行四边形，通过圆与所拼成的近似的长方形或平行四边形之间关系的对比，最终得出圆的面积计算公式。但在新中国成立前革命根据地的小学数学教科书中，除了这种方法，还曾经出现过不一样的教学法，本文中分别称它们为细分求和法、重叠比较法和构造推断法。这些教学法，虽然在现行的教科书中很少出现，但在关注学生核心素养培养的今天，显得很有意义。

[一、细分求和法]

“化圆为方是一个比较难的问题，不过我们也可以想法求出它的近似值来，像下面的图，在圆内作许多直径，相邻两半径中间夹着一个平面图形，近似一个三角形，圆的半径相当于三角形的高，圆周相当于各三角形的底，求出图中三角形的总面积就得到圆的面积。”[1]这是晋察冀边区行政委员会教育处审定的《算术课本（高级小学适用 第四册）》中的内容，所述之图如图1所示。这样的教学法，也见于陕甘宁边区、晋冀鲁豫边区、华北解放区、东北解放区、山东解放区的小学数学教科书中，可见这是当时圆面积计算教学中的一种主流方法。

上述方法可以追溯到公元前3世纪阿基米德所写的《圆的度量》[2]。据笔者所考，我国小学数学教科书中最早出现此方法，是在1918年的《最新高等小学教科书 数学拾级（中卷）》上[3]。分析上述过程可发现，其基本思路是“细分求和”。当然，分得越细，精确度越高，也就是每个扇形的弧长与三角形的底越接近，扇形的半径与三角形的高越接近，当然最后计算出的结果也越接近圆面积的精确值。

从数学的视角看，上述过程不仅是一个解决问题的过程，更是一个数学思想与方法渗透的过程，因为其中不但渗透了无限与极限的思想，而且这种“细分求和”本质上是高等数学中定积分思想的雏形，学生在后续学习定积分时，或许会勾起对这种方法的回忆，按现时的说法，这是一种数学经验的积累；如果从哲学层面分析，这种“细分求和”的思想与方法实质上对应的是一个分与合的过程，它渗透了辩证统一的思想，具有方法论的意义。学生通过数学知识的学习，要获得数学的思想与方法，乃至更一般的思想与方法。因此，这种圆面积计算教学法，在当今仍然有重要的意义。

[二、重叠比较法]

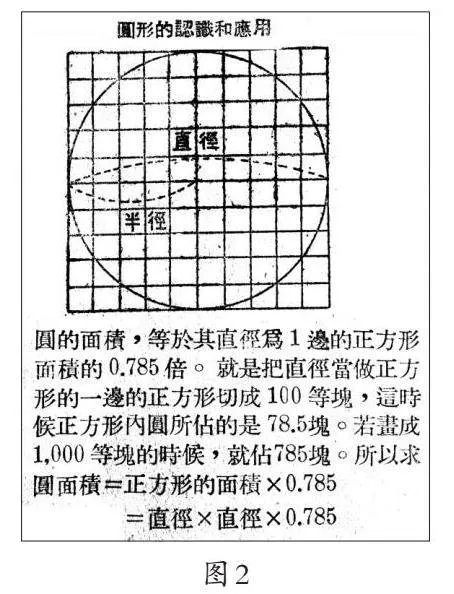
图2所示是由东北行政委员会教育部编写，1949年东北新华书店出版的《初小算术（第八册）》中关于圆面积计算教学的描述[4]。

由图可知，上述方法把圆置于一个边长与圆的直径相等的正方形中，通过与正方形面积大小的比较，近似地求出圆的面积。

这种方法，由于圆边界处小方格的计数较难精确，所以很容易让人产生对利用“直径×直径×0.785”计算所得结果精确性的怀疑。事实上，它是π取3.14时πr2的另一种表示形式。在当时数学（算术）教学要为实际生活、生产服务的背景下，这是一种非常有价值的方法。我们知道，在解决实际问题的过程中，数学计算有时不需要也不可能做到百分之百精确。对小学数学来说，有时也不需要精确计算，而需要的是解决问题的思想与方法。

与一般的圆面积计算教学法相比，重叠比较法最大的特点是没有用到圆周率。这种方法至少有如下几点值得我们思考与借鉴。

一是更有利于学生对面积概念及其基本求法的掌握。我们知道，计算一个图形面积最基本的方法，就是把这个图形放在由单位面积的正方形所组成的方格图上，然后数出这个图形所占的方格数。这种方法看似笨拙，却具通用性；看似原始，却是图形面积概念本质的反映。学生在此前遇到的面积计算问题，其中图形的边都是直的，圆面积计算是学生首次接触的曲边图形面积计算，所以再次用这种最基本的方法求面积，可以让学生体会到这种原始方法的普适性，从而进一步加深对图形面积概念的理解。

二是隐含着解决问题方法的教学。从解决问题的角度看，当新问题不能直接解决时，我们往往会想办法把它转化为以前碰到过的能解决的问题，然后通过后者的解决来达到前者的解决，或者借助后者的功能（特征）来解决前者。当然，这两者之间往往具有一定的联系，只有抓住这种联系，才能使问题迎刃而解。

在这里，圆面积的计算是一个新问题，正方形面积的计算是一个早已解决的问题。如何把圆面积的计算问题转化成一个与正方形面积相关的问题呢？关键是找到正方形与圆之间的联系，而这种联系就是正方形的边长与圆的直径相等这一关系。利用这种关系，我们把圆放到正方形上，通过比较两者单位面积重合的个数，确定圆的面积。正如图2所示，把正方形切成100等份时，圆中有78.5份这样的小正方形与它重合，把正方形切成1000等份时，圆中有785份这样的小正方形与它重合，从而得出圆的面积等于以其直径为边长的正方形面积的0.785倍。最后根据这种关系，得出圆面积等于“直径×直径×0.785”的结论。对学生来说，圆和正方形间的这种显性关系是容易找到的。

三是能让学生进一步加深对圆与正方形之间关系的理解。圆和正方形分别是曲、直两类平面图形中基本的图形，尽管学生在日常生活中或在以往的数学学习过程中，经常接触这两种图形或由这两种图形组合而成的图形，但对它们只有直观的、浅层次的认识。由上述分析可知，我们看到的正方形外切于圆，其实是它们显性关系——长度关系（边长等于直径）、隐性关系——面积关系（约1000∶785）的一种表示形式。

[三、构造推断法]

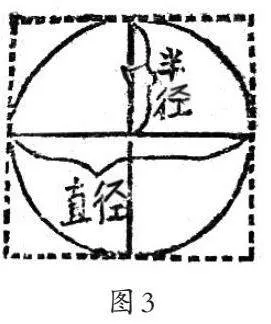
图3是晋冀鲁豫边区教育厅审定的《算术课本（高级 第二册）》中关于圆面积计算教学的插图，其文字阐述是“由圆心引出纵、横两直线，把圆形割成4等份，再把每个等分形依照圆的半径各扩充为4个小方形，每个小方形的面积，都是一边自乘，也就是圆形的半径自乘。4个小方形合起来和圆形的全部比较，我们可以看出圆外扩充出来4个‘角’，把它们拼合起来，不到1个小方形的大小，所以圆面积是半径的自乘4倍不足，3倍多一些。上次所讲的圆周率3.1416，就是这个意思”[5]。然后，在以用算式“5尺×5尺×3.1416＝78.54（方尺）”解决“求半径为5尺的桌面面积是多少”为例的基础上，得出“圆面积＝半径×半径×3.1416”。

这种方法的特点是根据圆的特征，构造了4个边长等于其半径的正方形，通过圆与4个正方形面积之和的比较，推断出“圆面积是半径的自乘4倍不足，3倍多一些”的结论。整个过程中，先构造，再推断。尽管这个结论的出现，给人一种灌输之感，但这种解决问题的方法，给我们对圆面积计算教学的设计打开了新的思路。

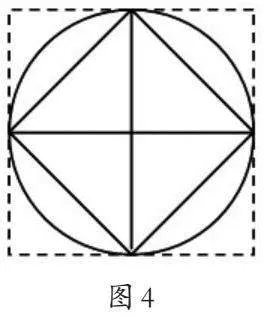
在得出“圆面积是半径的自乘4倍不足”，即比4个这样的正方形面积之和小之后，我们可以引导学生思考“比几个这样的正方形面积之和大”的问题。一般来说，学生会从图3中发现，只要把每个正方形都去掉一半，如图4，就可得出圆的面积比2个这样的正方形面积之和大，也就是2r2<S圆<4r2。当然，学生此时会自然地想到“会不会比3个这样的正方形面积之和大”（即 3r2<S圆<4r2）的问题，于是教师引导学生观察、讨论“圆外扩充出来的4个‘角’拼合起来”是否真的“不到1个正方形的大小”，再用如上的重叠比较法推出圆的面积。以r=10厘米为例，让学生数出圆面积大约在300多平方厘米，并推断出若r=1厘米则圆的面积大约是多少，以验证并求出这个比3大一点儿的数可能是几，从而理解“上次所讲的圆周率3.1416，就是这个意思”。最后，像得出圆周长计算公式（方法）那样，得出圆面积的计算公式（方法）。

笔者认为，这个以“构造推断”为蓝本的圆面积计算教学设计，在让学生获得圆面积计算公式（方法）的过程中，凸显了如下三方面的意图。

一是让学生从另一个侧面认识圆周率。学生对某个知识点的深刻理解并真正掌握，只有通过多角度的认识与思考才能达到。显然，这样的教学可使学生进一步认识到圆周率也是圆面积和半径平方的比，并为其后续学习打下更扎实的基础。

二是让学生的探究基于理性认识。由上可看出，学生对圆周率也是圆面积与半径平方的比之探究，是建立在3r2<S圆<4r2的认识基础上进行的，而这恰恰是圆面积计算教学中容易被大家遗忘的一个盲点。因为学生的探究或操作，只有建立在一定的理性认识基础之上，才更有数学味，才是真正意义上的数学探究。

三是数学思想与方法的渗透。在构造推断法中，圆周率的求得，是通过圆的面积比4个以其半径为边长的正方形面积之和小，而比2个这样的正方形面积之和大、比3个这样的正方形面积之和大等范围的缩小，最后想办法求出它的近似值。这种逐步缩小范围、逐步逼近的方法，在数学中是一种经常被使用的方法，其思路也被广泛应用于现实生活中各种问题的解决，如案件侦破等。再深一层看，这就是刘徽所用“割圆术”的雏形。因此，这样的教学也体现了在教学中渗透数学思想与方法。

教科书对某个知识点处理方式的呈现，不仅蕴含着基本的教学思路和方法，更承载着某个时期的教学理念，特别是编写者所倡导的理念。革命根据地小学数学教科书中的三种圆面积计算教学法，如果从数学思想与方法及数学本质的角度来看并不过时，值得我们借鉴。

参考文献：

[1]晋察冀边区行政委员会教育处.算术课本：高级小学适用 第四册[M]. 张家口：新华书店晋察冀分店，1946.

[2]迈克尔·J.布拉德利.数学的诞生：古代—1300年[M].陈松，译.上海：上海科学技术文献出版社，2008.

[3]刘光照.最新高等小学教科书 数学拾级：中卷[M].上海：上海美华书馆，1918.

[4]东北行政委员会教育部.初小算术：第八册[M].沈阳：东北新华书店，1949.

[5]晋冀鲁豫边区教育厅.算术课本：高级 第二册[M].左权：华北书店，1944.

【本文系浙江省教研课题“百年小学数学教科书发展研究”（编号：G2020122）、嘉兴市教科规划专项课题“革命老区小学数学教科书研究”（编号：JZ18122）的研究成果】

（作者单位：浙江海盐县教育研究中心）