借助数学游戏，提升思维能力

2022年版课标指出：“数学是人类文化的重要组成部分。”数学游戏是数学文化的一种独特表现方式。将数学游戏应用于小学数学教学中，不仅符合学生的认知特点，更符合人文素养培养的要求。在“神奇的魔法纸牌”一课中，学生在玩游戏的过程中不断探索规律，猜测、验证，从而发现其中的秘密。这样不仅激发了学生学习数学的兴趣，更有助于发展学生的思维品质，提升学生的思维能力。

一、游戏探究，培养猜测能力

（一）了解游戏规则。

教师出示：将若干张牌按顺时针方向从小到大排成一圈，从1号牌开始抽起，按照隔1张抽走1张的方法，最后留下的是哪张牌呢？

师生一起解读游戏规则，重点理解“从1号牌开始”“隔1张抽走1张”。

教师请一个学生选择牌的数量（以下简称牌数），然后师生一起猜最后留下的是哪张牌，随后一个学生上台演示验证，发现老师猜对了，由此学生对老师敬佩不已，对游戏充满疑惑。

（二）玩游戏并记录。

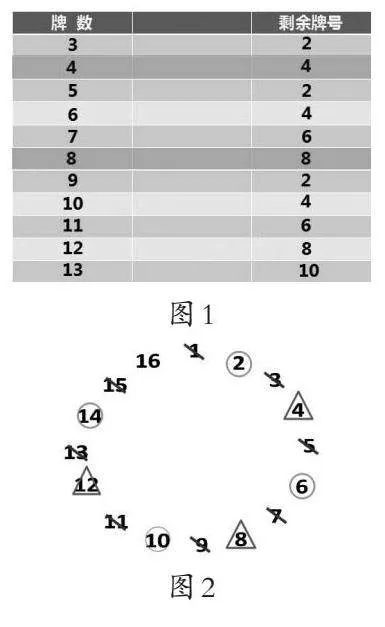
教师给每个小组发13张纸牌（牌号为1～13）。学生以四人小组为单位，先由组长抽出牌数，再由组员猜测剩余牌号（最后留下的牌的号码），然后进行验证，并把结果记录下来。学生记录的结果如图1所示。

（三）观察并归纳。

1.发现特殊牌数的特征。学生观察表1，发现剩余牌号都是偶数。经过分析，发现原因是牌号为奇数的牌全被抽走了。学生还发现，牌数是4和8时，剩余牌号与牌数相等，并称这样的牌数为特殊牌数，这为探究非特殊牌数的规律做好了铺垫。

2.揭示非特殊牌数的规律。教师引导学生观察牌数从5到8时的情况。学生发现，牌数由5变为6时，剩余牌号增加2；牌数由6变为7时，剩余牌号又增加2；牌数由7变为8时，剩余牌号又增加2。学生通过分析发现：（5-4）×2=2，（6-4）×2=4，（7-4）×2=6，（8-4）×2=8。

二、动手操作，培养验证能力

（一）激发验证需求。

在学生发现特殊牌数4、8以后，教师继续引导。

师：你认为这样的特殊牌数还有没有？

生：16也是一个特殊牌数。

师：你怎么想到的呢？

生：8是4的2倍，我猜想下一个特殊牌数是8的2倍，所以我猜想下一个特殊牌数是16。

师：16是不是特殊牌数呢？我们该怎么办呢？

学生马上想到需要验证。

（二）积累验证方法。

1.学生利用画一画验证16确实是一个特殊牌数（如图2）。接下来，学生又发现了特殊牌数32、64等，并且这样的特殊牌数有无数个。

2.当学生知道5、6、7这些非特殊牌数的规律后，教师追问：9～13这些牌数有没有这样的规律？学生猜测，然后验证，发现它们也有这样的规律。

3.当学生观察剩余牌号点子图（如图3）以后，教师引导学生猜测规律。学生从点子图上发现剩余牌号是按照牌数一段一段有序分布的。

三、直观表征，培养逻辑推理能力

（一）直观助推思维。

教师引导学生观察点子图（如图3）。

师：牌数在哪里？剩余牌号又在哪里？

生：最下面一行表示牌数，上面的这些点表示牌数对应的剩余牌号。

师：你还有什么发现？

生：剩余牌号是一段一段分布的。

生：我发现每一段最高的牌号是特殊牌数，最低的牌号是2。

师：那么下一段对应的牌数是从几到几？

生：根据前面的规律，我认为应该是从17到32。

（二）想象提升思维。

学生通过观察发现点子图上剩余牌号是一段一段分布的，每一段最高到达特殊牌数，最低是2。

师：你觉得要找到剩余牌号，关键是什么？

生：关键是找到特殊牌数。因为只要知道特殊牌数，我们就可以推出其他的非特殊牌数，也就知道了剩余牌号是几。

师：观察点子图，接下来的特殊牌数是多少呢？

生：32。

师：你是怎么思考的呢？

生：因为牌数从3到4是一段，从5到8是一段，从9到16是一段，所以我推断接下来应该从17开始，到32结束。

师：再往后呢？

生：从33开始，到64结束。

四、已知换未知，培养逆向思维能力

在数学学习过程中，数学知识的形成与发展之间是双向的，只有双向思考才能拓展学生的思维。在思考问题时，我们既可以正向思考，也可以逆向思考。因此，在教学中采取已知与未知互换的方式，引导学生从中发现问题，进而在解决问题的过程中培养逆向思维能力。

学生通过猜测和验证、推理、归纳等方法，已经会通过牌数找到剩余牌号，这是一种正向思维。

师：如果最后留下的是14号牌，那么你觉得老师要准备几张牌呢？

生：我们只要找到特殊牌数就可以了，因为非特殊牌数都是在特殊牌数上展开的。

生：因为16张牌时剩余牌号是16，所以15张牌时剩余牌号是14。

同时学生发现牌数越多，越难找到特殊牌数，那么怎样快速找到特殊牌数呢？经过观察，学生发现2是最小的特殊牌数，其他的特殊牌数分别是：4=2×2，8=2×2×2，16=2×2×2×2……

根据剩余牌号推导牌数，对学生来说是一次逆向分析的过程，这样发展了学生的思辨能力。教师要善于把握恰当的学习时机，借助巧妙的教学手段，把已知与未知进行合理互换，这样学生的逆向思维能力将不断提高，分析问题时也会更加全面。

综上所述，数学游戏课在学生的思维能力培养方面有独特优势，教师要善于利用数学文化资源，引导学生进行分析、归纳、推理、猜测、验证，不断提升思维能力。

参考文献：

[1]刘琳娜.数学文化在教学中的运用[J]．基础教育课程，2021（2）．

[2]付天贵，宋乃庆.走向小学数学文化自觉的思考[J].数学教育学报，2019（6）．

[3]刘璇，潘亦宁.小学数学游戏课的教学设计[D].成都：四川师范大学，2016.

[作者单位：杭州师范大学附属乍浦实验学校（小学部）]