聚焦核心问题 促发深度学习

“三角形的分类”是苏教版教材四年级下册第七单元的内容，笔者在教学本课时，重点聚焦提炼核心问题，以核心问题引领学生思考，促进学生的深度学习。

【教学片段】

一、明确分类标准

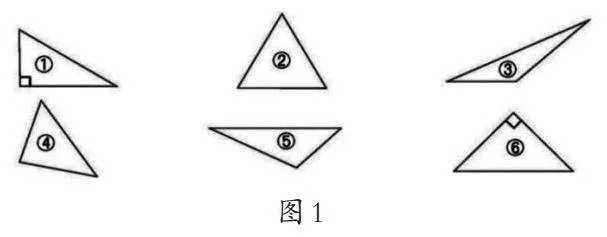
屏幕上出示6个三角形。（如图1）

师：这6个三角形的形状相同吗？大小相等吗？它们有什么共同的特点？

生：这些三角形都有3个顶点、3条边和3个角，内角和都是180度。

师：这些三角形可以按什么标准来分类？

生：可以按角来分类。

师：这节课，我们就根据角的特点来研究三角形的分类。

二、学生自主分类

师：想自己先尝试把这6个三角形分类吗？

生：想。

师：那请听好操作要求。

屏幕上出示操作要求，播放录音：

（1）看一看：每个三角形的3个角分别是什么角？

（2）想一想：哪些三角形的角有共同特点，可以分为一类？

（3）分一分：动手把学具袋里的6个三角形在课桌上分一分。

（4）说一说：和同桌说一说你是怎么分的。

学生分类，教师巡视。

三、讨论分类结果

师：谁愿意上来，用黑板上的大三角形，边分边交流你的分法？

生：我分成了3类：①号和⑥号分为一类，它们的3个角分别是直角、锐角、锐角；③号和⑤号分为一类，它们的3个角分别是钝角、锐角、锐角；②号和④号分为一类，它们的3个角都是锐角。

师：找得真准。第1类这样的三角形，我们称作直角三角形；第2类，我们称作钝角三角形；第3类，我们称作锐角三角形。

四、研究直角三角形

师：我们先来看直角三角形，想一想，什么样的三角形是直角三角形？

生：有1个角是直角的三角形是直角三角形。

生：有1个直角、2个锐角的三角形是直角三角形。

师：出现了两种不同的说法，比一比，这两种说法的区别在哪里？

生：第2种说法比第一种多说了“2个锐角”。

师：这里的“2个锐角”能省略不说吗？为什么？先独立思考，然后前后四人小组讨论一下。

学生小组讨论后全班交流。

师：来，交流一下你们的讨论成果吧，“2个锐角”可以省略吗？为什么？

生：2个锐角不能省略，因为三角形有3个角，不能只说1个直角。

生：我不同意他的说法，三角形内角和是180度，1个角是直角，另2个角的和是90度，那这2个角就一定是锐角，不用说也知道。

生：我也觉得不用说，因为三角形里不可能有2个直角，2个直角就180度了，也不可能既有直角又有钝角，所以另2个角一定是锐角，不用说。

……

师：同学们思维真活跃啊。在刚才你们各抒己见的过程中，出现了两种观点，那究竟“2个锐角”能否省略不说呢？我们一起来看。

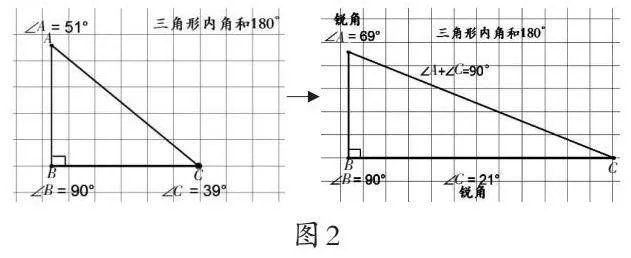
几何画板演示：（如图2）

师：三角形内角和是180度，∠B是90度，那么∠A和∠C不管大小怎么变，它们的和都是90度。所以∠A和∠C一定是锐角。

师：那再想象一下，三角形里可能有2个直角吗？可能有1个直角和1个钝角吗？

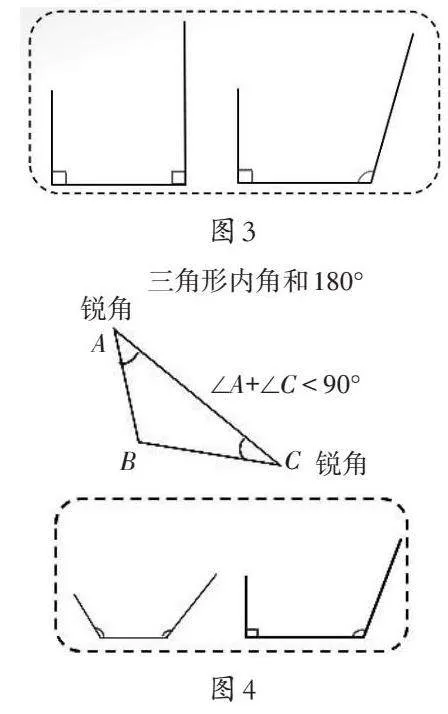
媒体直观演示：（如图3）

师：综合三角形内角和推理和想象画图可见，三角形中只要有1个角是直角，另外2个角一定是锐角，所以，“2个锐角”能省略不说吗？

生：能！

师：那什么样的三角形是直角三角形？哪种说法更好一些？

生：第一句话。

师：对，数学上就是用“有1个角是直角的三角形是直角三角形”来描述的，这样描述既准确、严谨，又简洁。

五、研究钝角三角形

师：那什么样的三角形是钝角三角形？

生：有1个角是钝角的三角形是钝角三角形。

师：这么简洁，那这里的“2个锐角”，为什么又不说呢？

生：三角形内角和是180度，1个角是钝角，另2个角的和就小于90度，那这2个角就一定是锐角，不用说也知道。

生：三角形里不可能有2个钝角，也不可能既有直角又有钝角，所以另2个角一定是锐角，不用说。

课件直观演示：（如图4）

师：你们真会举一反三，可见，三角形中有1个钝角，另2个角一定是锐角，“2个锐角”能省略不说。

六、研究锐角三角形

师：那什么样的三角形是锐角三角形呢？

生：有3个角是锐角的三角形是锐角三角形。

师：你们都是这么想的吗？

生：是的。

师：哎，直角三角形只要说有1个角是直角，钝角三角形只要说有1个角是钝角，请思考：锐角三角形为什么要说3个锐角呢？同桌讨论一下。

学生讨论后反馈。

生：锐角三角形要说3个锐角，直角三角形里有锐角，钝角三角形里也有锐角，如果只说1个锐角的话，不确定一定是锐角三角形。

生：我发现，每个三角形中至少有2个锐角，第3个角是直角，就是直角三角形；第3个角是钝角，就是钝角三角形；第3个角是锐角，才是锐角三角形，所以要说3个锐角。

……

师：对呀，三角形中至少有2个锐角，只有当三角形中的第3个角是锐角，也就是3个角都是锐角的时候，这个三角形才是锐角三角形。所以，在描述锐角三角形时一定要说清楚3个锐角。同学们的思维真严谨。

【教学思考】

一、基于认知规律，重构学习序列

苏教版教材安排的教学顺序是先认识锐角三角形，再依次认识直角三角形、钝角三角形。但在这3类三角形中，直角三角形最特殊，并且在认识角的时候，也是先认识特殊的角——直角。从特殊到一般认识事物符合学生的认知规律。于是，在教学设计时，重构了学生知识学习的序列，先充分展开过程认识直角三角形，同时鉴于直角三角形和钝角三角形的本质属性有相同之处，于是接着认识钝角三角形，引导学生运用直角三角形的认知方式来迁移学习，最后认识锐角三角形。这样安排，从特殊到一般，符合学生的认知规律，同时也沟通了角的认识与三角形认识新旧知识之间的联系。

二、梳理知识点，提炼核心问题

研读教材，梳理本节课的知识点：明确直角三角形、钝角三角形、锐角三角形的特征；理解1个三角形中只可能有1个直角或1个钝角，每个三角形中至少有2个锐角，体会数学概念表达的合理性、严谨性和简洁性；体会按角的特点分类，只能分成这3类的合理性。其中3类三角形的定义，3类三角形的判断，都是比较简单的知识和技能，而为什么定义直角三角形和钝角三角形时可以省略“2个锐角”，而定义锐角三角形时为什么要描述“3个锐角”，探究这两个“为什么”是对三角形本质的追问，也是最能发展学生核心素养的学习过程。因此，把“这里的‘2个锐角’能省略不说吗？为什么”和“锐角三角形为什么要说3个锐角呢”这两个问题确定为本节课的核心问题，以核心问题引领学生思考。

三、聚焦核心问题，促发深度学习

本节课紧紧围绕上述两个核心问题设计问题序列，展开逐层深入、环环相扣的思考与辨析，并开展交流讨论，引发学生的思维碰撞。有的学生利用三角形内角和知识进行推理，在直角三角形中1个角是直角，其余2个角一定是锐角；有的学生通过直观画图体验的方式，如果1个三角形中有2个直角或者钝角就围不成三角形，反过来说明直角三角形中有2个角一定是锐角。学生或补充，或修正，或质疑，或肯定，在深度对话中相互启发、相互完善。在争论思辨中，学生的认识走向深入，不仅知其然，而且知其所以然。在这个过程中，学生的思维在“爬坡”，思想在“登顶”，学生对知识的认识从模糊逐渐走向清晰，学生的思维从肤浅逐渐走向深刻。

（作者单位：江苏宜兴市第二实验小学）