问题引领重说理 数形结合促提升

一、开门见山，唤醒经验

师：今天我们学习“找规律”（板书），以前我们也学习过“找规律”，能举例说说什么是“规律”吗？

生：比如一组数，从小到大排列，它们之间相差的数一样。

师：你的意思是，这组数的大小在变化，但它们之间的差是不变的，“变化中的不变”就是规律。那怎么找这组数的规律呢？

生：可以观察前几个数的特点，算一算它们之间的差，就能找到规律了。

二、观察推理，初探规律

1.从“数”出发，感知规律。

师：（板书：1）能看出规律吗？

生：只有一个数，不能看出规律。

师：（接着板书：4）能看出规律吗？

生：相差3，但不一定就是规律。

师：看出了一些规律，但不能确定。怎么办？

生：再写一个数。

师：（接着板书：9）能看出规律吗？

生：相差5，每次相差的数都多2。

师：能确定规律吗？（生：能）那你们猜猜下一个数是多少。

生：16，因为1+3=4，4+5=9，9+7=16。

生：我也认为是16，不过我是这样想的，因为第一个数是1×1，第二个数是2×2，第三个数是3×3，那么第四个数就是4×4，所以是16。

师：能确定是16吗？（生：能）看来要确定一组数的排列规律至少需要写出几个数呀？

生：至少写出3个数。

师：那再下一个数又会是多少呢？对应的算式是什么？

学生答略，教师用课件演示验证。

2.类比推理，发现规律。

师：照这样想下去，第10个数是几？第100个数是几？

学生答略，教师用课件演示验证。

师：如果是第n个数呢？

生：第n个数就是n×n。

师：归纳一下，这组数的排列规律是什么？

生：是第几个数，就用几乘几。

师：不管这组数怎么变化，有一点是不变的，也就是用序号乘序号，就得到了这个数。（板书：序号×序号=这个数）

3.数形结合，理解规律。

师：还可以通过图形来理解这组数的规律。

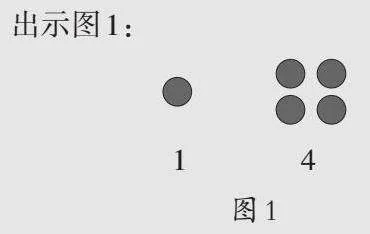
出示图1：

师：你能照样子画出9、16、25这些数吗？

学生独立画图，然后集体反馈。

师：像这样，每个图形都是一个点阵（板书：点阵）。仔细观察每个点阵的形状和点数，你发现了什么？

生：我发现每个点阵都是正方形。

生：第1个点阵是1行1列，点数是1×1；第2个点阵是2行2列，点数是2×2；第3个点阵是3行3列，点数是3×3；第4个点阵是4行4列，点数是4×4。依次类推，第n个点阵是n行n列，点数是n×n。

生：序号是几，点数的算式就是几乘几，图形就是几行几列。

师：借助图形能直观地看出“变化中的不变”，这个规律跟刚才我们发现的乘法规律是一致的。

三、多角度观察，再探规律

1.自主探究，用多种形式表示规律。

师：如果换个角度观察这组“形”和“数”，你又能发现什么呢？

教师出示活动要求：

①想：点阵图有怎样的排列规律？怎样用算式表示？

②画：必要时可以在点阵图上画一画、分一分。

③写：把你的发现用算式表示出来。

④说：写完后在小组内说一说。

学生自主探究，教师巡视指导并收集典型作品，全班交流。

教师展示作品1：（如表1）

师：能看懂这位同学的算式和发现吗？有没有疑问？

生：我想问，②号图形里的“1”在哪里？“3”又在哪里？

生：“1”是上一组图形中点的个数，“3”是直角边上点的个数。

学生在图形上标注，教师借助课件演示。

师：②号图形的算式是1+3，③号图形的算式是1+3+5，④号图形的算式是1+3+5+7，照这样下去，下一个图形要继续加几？

生：加9。

师：大家不仅会观察，还学会了推理。仔细观察这些算式，还有什么发现？

生：我发现它们都是单数。

师：单数也就是奇数，再看看这些奇数，有什么特点？

生：都是连续奇数相加。

生：我发现序号是几，算式中就有几个奇数相加。

师：你发现了点阵的序号与加数个数的关系。再看看，这些算式都是从几开始加起的？

生：从1开始。

生：我发现②号图形的算式是1+3，“1”表示的就是①号图形中的1个点；③号图形的算式是1+3+5，1+3是②号图形中的点数，④号图形的算式是1+3+5+7，1+3+5是③号图形中的点数。

师：也就是说后面的图形都是在前面图形的基础上再增加点数得到的，看来这个起始的“1”很重要。（出示：1+3+5+7+9+11+13+15）按照这样的规律，这个算式表示的是第几个图形？

生：第8个。

师：你是怎么知道的？

生：因为算式里有8个加数。

生：只要数一数一共有几个加数，就知道它表示的是第几个图形。

师：看来图形序号和算式中加数的个数有确定性的关系。

教师展示作品2：（如表2）

师：你能看懂他是从哪个角度观察的吗？

生：他是斜着观察的。②号图形画了两条斜线，把点分成了三部分，算式是1+2+1；③号图形画了四条斜线，把点分成了五部分，算式就是1+2+3+2+1。每次都是从1加到序号数，再从序号数加回到1。

生：②号图形，算式中的最大数就是2；③号图形，最大数是3；④号图形，最大数是4。最大数就是序号数。

师：看来，算式中的最大数与图形的序号也有着确定性的关系。

2.回顾梳理，感悟思想。

师：刚才我们借助图形研究这组数，谁来和大家分享一下有什么感想？

生：观察的角度不同，得到的规律不同，算式也不同。

生：算式都和序号有关系。

生：不管是哪种算式，得数是相同的。

教师小结：同样的数，同样的图形，观察的角度不同，规律的表示方式也不同。

四、巩固应用，深化对规律的理解

1.不同形式之间的互相转化。

师：既然是同一组图形规律的表示方式，它们之间会不会存在某种关系呢？你能不能将其中一种转化成另一种？

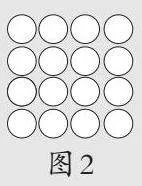
出示图2和三个算式：

（1）1+3+5+7。

（2）1+2+3+4+3+2+1。

（3）4×4。

师：计算图形中的点数，哪种方法更简单？

生：4×4。

师：再遇到1+2+3+4+3+2+1这样的算式，你会怎样计算？

生：4×4。

师：有了这样的发现，试一试下面几道题怎样计算更简便。

课件逐一出示：

（1）1+2+3+4+5+6+5+4+3+2+1=

（2）1+3+5+7+9+11=

（3）1+3+5+7+9+…=

（4）1+2+3+…+99+100+99+…+3+2+1=

2.揭示概念，渗透数学文化。

师：刚才我们研究的点子图都是正方形的，所以像1、4、9、16这样的数也叫作正方形数（板书）。那你能再说出一个正方形数吗？

学生答略。

师：我们今天研究的正方形数，被称为“有形状的数”——形数。公元前6世纪，古希腊的毕达哥拉斯学派倡导“万物皆数”的观点，认为世界上所有事物都与数有关系。在众多的数中，有一种非常有趣的数——形数，也就是与图形有关的数。他们在沙滩上用小石子摆几何图形，从而发现了图形与石子数量之间的关系。

五、回顾反思，总结提升

师：这节课我们研究了“有趣的‘形数’”，你都学到了什么？

生：从不同的角度观察，规律不同，表示的算式也不同。

生：算式与算式之间可以相互转化。

师：你还有什么问题想问吗？

生：除了正方形数，还有其他形状的数吗？其他图形的点子数又有什么规律？

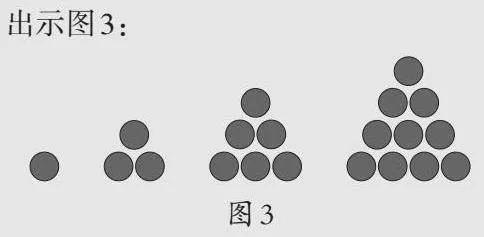
出示图3：

师：这些三角形的点数分别是几？

生：1、3、6、10。

师：知道它们是什么数吗？

生：三角形数。

师：正确！类似这样的点阵还有很多。（出示：长方形数、五边形数、六边形数）从它们当中，你又能发现哪些规律？请同学们用今天所学的探究规律的方法，课后探究思考。数学把自然规律抽象成一幅简洁准确的图形。希望在今后的学习中，用你的数学眼光，去寻找数学中的美；用你的数学思维，去探究数学中的规律。

（作者单位：北京亦庄实验小学）