幼小衔接聚焦“三化”，涵养学生核心素养

2022年版课标要求“注重幼小衔接……合理设计小学一至二年级课程，注重活动化、游戏化、生活化的学习设计”。课程“活动化、游戏化、生活化”（即“三化”）契合刚入学儿童的年龄特点，遵循儿童的发展规律。然而，在核心素养导向下，幼小衔接中还需厘清“三化”与核心素养的关系，教学中不能只为简单迎合儿童的喜好，而要帮助他们学习进阶，促进思维发展才是衔接的关键。因而，要把课程设计中的“三化”与核心素养无缝对接，共生共融。下面以苏教版教材一年级下册“认识单数和双数”一课为例谈谈我们的实践探索。

一、情境生活化，用数学眼光努力发现

情境的生活化源于数学来自生活，从生活现象变为数学问题，从具体情境变为抽象思考，这是儿童数学学习的起点。在生活化情境中，要孕伏数学思想，激发数学思维，巧设情境，引发儿童用数学的眼光，抽象数学现实，发现数学规律。

“认识单数和双数”安排在一年级下学期的练习课中，教师了解到学生在幼儿园初步学习过单数和双数，但仅限于在游戏中认识单数和双数，知道判断10以内单数和双数的方法，至于单数和双数的含义、判断的依据、排列的规律、在生活中的应用等没有涉及或只是简单了解。立足科学衔接，一道练习题，一个知识点，我们可以做哪些数学探索丰盈儿童对单数和双数的认知，使学生体会数学的好玩与价值呢？

1.生活情境：经历中提取概念本质。

课前教师和学生聊天，明确今天要学习单数和双数。学生热情高涨，都说学过，知道2、4、6、8、10是双数，1、3、5、7、9是单数。还有学生知道通过数的末尾确定单数和双数。教师追问：“你们知道为什么2、4、6、8、10是双数，而1、3、5、7、9都是单数吗？”“为什么只要看末尾判断？”学生一下子被问住了，个别学生的解释含糊不清。

疑问是学习的起点，研究是学习的钥匙。课堂伊始，学生带着问题从学校倡导的劳动实践开始：家里凌乱的鞋子和袜子，该怎样整理呢？小朋友结合生活经验，很快2只1双整理好（鞋子和袜子以图的形式出现，学生操作配对。图略）。鞋子8只整理成4双，但袜子只有7只，只能整理出3双，落单1只。教师追问：“为什么这样整理？”学生在操作之后思考整理的依据，也就是2只要配成1双，此时生活经验与数学思考对接。学生悟出单数和双数的本质就是2个2个地数能不能正好数完，两两配对的操作和2的倍数关联起来。

整理的过程只是基于生活常识，教师进一步让学生把整理的过程记录下来，每2只用笔圈在一起，一边圈一边2只2只地数，眼口并用，强化概念的要素。教师追问最后1只袜子为什么没有圈。从操作到反思，单数2只2只地数，有1只无法配对的具象样态因追问而印刻在学生的脑海里。

2.生活元素：体验中建构概念内涵。

练习巩固也可以通过有趣的生活情境巧妙完成。概念的形成需要一个不断感悟体会的过程，利用生活元素，分一分、想一想、做一做。保持与例题的情境一致的同时，也自然巩固了新知。

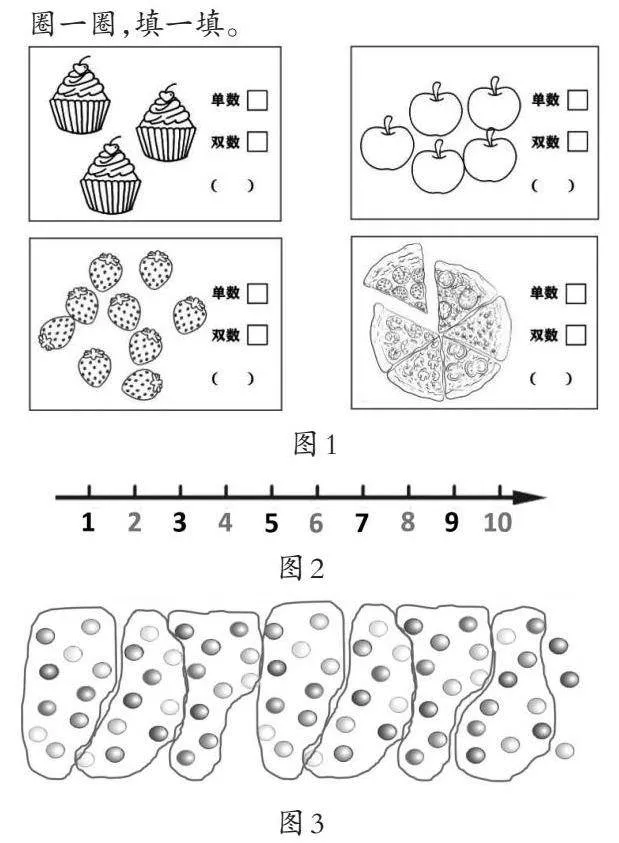
课上教师邀请小朋友分零食（如图1）。该怎样圈一圈才能一眼看出是单数还是双数呢？

提问中强调了“一眼看出”，规避了学生简单通过数数直接判断，根据学习经验，学生模仿鞋子和袜子的操作方法，利用每2个一圈看是否落单进行判断。操作伴随着思维，生活与概念呼应。学生在图1的4幅图的圈画中不断建构单数和双数的表象，最终形成对单数和双数概念内涵的理解，即2个2个地数正好数完是双数，2个2个地数有1个落单就是单数，并能总结出判断单数和双数的关键是2个2个地数看有没有剩余。基于生活化的学习，不仅解决了学前儿童的认知盲区，启迪儿童用数学的眼光发现与思考，同时为五年级认识奇数和偶数预留通道，数感也在生活化的学习中得到发展，数学核心素养的全局性、阶段性和发展性得以体现。

二、学习活动化，用数学思维积极思考

活动化是以活动为载体，通过儿童喜爱的方式进行数学学习。因而数学活动承载着数学任务，数学活动化更要富含数学思维。

1.设计活动：揭秘规律背后的数理。

单数和双数的排列是有规律的，规律背后也有数理可循。认识了10以内的单数和双数后，教师把所有的数都请到数轴上（如图2），学生观察单数和双数的排列规律。

学生不难发现单数和双数是间隔排列的，为什么有这样的规律呢？几个学生的回答都有悱而不达的感觉，于是教师设计了抱一抱的活动。邀请8个学生走上讲台，教师带着大家一起数人数，要求学生2人一抱。学生边数边观察，数到1，落单；数到2，1、2合抱；数到3，落单；再添1人，数到4，3、4合抱……单数和双数间隔排列规律在抱一抱中破解了，2个2个地数，落单后再添1人又能2人一抱，单数变成双数。单数和双数排列的规律是因为它们的意义而生成的，巧妙的活动设计，虽没有人人参与，但是在教师的有序组织下，学生带着疑问和思考，观察活动现象，规律背后的数理清晰明了。

2.链接活动：探寻规则背后的依据。

本节课的教学是在一年级下学期，学生已经认识了100以内的数，单数和双数的认识不能仅停留在10以内，教学到此学生对单数和双数的意义已经感知得非常充分。于是，进一步把单数和双数的认识扩展到100以内。课堂上教师呈现认识100以内数时教材上曾经出现过的一幅珠子图。只看图学生一下子报不出珠子的颗数，教师启发学生用以前学习的方法10个一圈来数数（如图3）。

师：现在你能一眼看出是多少颗珠子吗？

生：73颗，73是单数。

师：为什么73是单数？

生：因为还剩3颗，3是单数。

师：明白了，你们就是看个位判断的，是吗？

学生频频点头。

师：有没有想过为什么前面都不用看，只看个位3就行了呢？

学生顿时面露难色，片刻思考后，教师组织大家进行小组交流。

生：你看前面都是10个一圈，10是双数，因为10颗珠子每2个一圈可以正好圈完，所以不用看。

“没有问题就是最大的问题”，数学学习的深入就是要不断追问为什么，把看似熟悉的数学现象变成一个个问号。学生借助10以内判断单数和双数的方法，链接100以内数数活动，依托直观图不难理解73为什么只看个位判断单数和双数。活动中的圈一圈，从10个一圈，到2个一圈，学生数数的活动经验在对知识的渐进式认知中不断积累，准确应用。同时，也为五年级探究奇数和偶数判断方法的道理孕伏了数理探寻上的方向。

三、应用游戏化，用数学语言解决问题

游戏化相对于活动化更关注学习活动的趣味性，从学前教育以游戏活动为主到小学入学之后学习游戏化，教学中要巧用游戏的形式让儿童掌握数学学习的方法和策略，形成数学语言，学会数学表达。

1.游戏现象：运用概念模型释疑解惑。

单数和双数在生活中无处不在，单数和双数的应用规律也藏在生活中。教学中教师试图用游戏的方式解密单数和双数的计算规律，目的是通过单数和双数模型，结合例子解释计算规律，感受数学探索的乐趣。

课堂上教师呈现拔河比赛的图片，请小朋友说说比赛规则，强调两队人数要同样多。接着教师提问：“两队合起来的总人数是单数还是双数？”有的学生说是单数，有的说是双数……许多学生的猜测是未经深入思考的，主要是根据一队人数可能是单数或双数来判断，没有考虑到求和带来的变化。于是教师请学生完成一个小研究：选择喜欢的方法，可以用圆片摆一摆，可以用笔画一画，也可以和同桌交流想法。大家在分享交流中认识到拔河比赛无论两边人数是单数还是双数，和都是双数，初步感知“单数+单数=双数，双数+双数=双数”的数学现象和道理。

2.游戏参与：借助数学经验完成挑战。

教学的最后环节是“白纸钻洞”的游戏：一支笔，一张白纸，怎样戳出单数个洞或双数个洞呢？学生面对挑战，迅速行动，在白纸上戳单数次，就会有单数个洞，同理也可以轻松得到双数个洞。教师接着提出挑战性任务：你能只戳一下，就得到双数个洞吗？思考片刻后，有个别学生想到了折纸，通过尝试大家发现对折一次、两次……纸就会变成两层、四层……这样戳一次打开就是双数个洞。

教师继续布置任务：怎样让同桌两人戳的洞数总和为单数？结合拔河人数的研究经验，学生猜测：两人戳的洞的个数一个是单数，一个是双数。教师请同桌合作尝试戳一戳，戳完通过计算，或者把洞两两配对验证自己的猜想，至此单数和双数求和的计算规律，学生全部在游戏中初步感受，未来在五年级学习奇数和偶数时一定能想起一年级那一次印象深刻的游戏探索活动，主动调取学习经验。

生活化、活动化、游戏化三者相辅相成，与学生核心素养的培育也不总是一一对应。“三化”着眼于“三会”，“三会”依托“三化”落地开花。在日常教学中，“三化”最终目标是要儿童实现从生活情境到数学抽象的水平数学化以及数学学习不断深入的垂直数学化。在幼小衔接的阶段潜移默化、循序渐进地帮助学生经历数学再发现的过程，养成讲道理、有条理的思维品质。

（作者单位：江苏南京市力学小学）